基于动力响应桥梁位移影响线识别方法分析
2022-10-24尚稳齐吴德义
尚稳齐,吴德义
(安徽建筑大学土木工程学院 安徽 合肥 230601)
0 引言
位移影响线是描述桥梁在单位移动荷载作用下的静态特性,是反映桥梁结构、材料强度特性的重要参数之一。桥梁在服役期间由于材料劣化、自然环境侵蚀、重复荷载等多因素的作用下,桥梁结构会不可避免产生一定损伤或者结构强度的退化[1],因此对桥梁进行承载能力试验来衡量结构的安全很有必要。因桥梁静载试验需要大量的人力、物力和财力,相关学者本着经济、快速的原则提出基于影响线对桥梁承载力评定的新方法[2,3]。
桥梁影响线可用于损伤识别[4,5]、模型修正[6]等问题的研究,因此识别与提取影响线的问题也至关重要。王宁波等[7]证实多项式分段拟合可应用于不同类型边界条件桥梁应变影响线的提取,同时该方法可有效剔除桥梁因动力响应的干扰。陈志为等[8]通过建立影响线识别的数学模型,通过Tikhonov正则化方法解决不适定问题,通过三次B样条曲线识别桥梁影响线。李东平等[9]通过引入轮胎—路面接触力分布模型,通过最小二乘法计算得到分段多项式模型,提取到桥梁准静态影响线。以上研究成果均有一定的参考与研究价值,但未形成普遍认可提取影响线的方法。由刘备等[10]利用经验模态分解与小波法来达到信号去噪的方法。本文提出以dbN小波变换、经验模态分解识别桥梁位移影响线,为相关研究人员提供多种位移影响线识别方法。
1 准静态影响线的识别
1.1 理论方法
车辆过桥所引起的动力响应是典型的车桥耦合问题,其中桥梁响应包括准静态部分和波动部分[11]。从动力学分析,以图1简支梁为例,其动力响应表达式,见公式(1)。
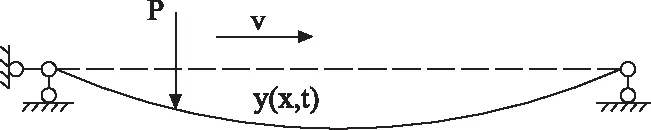
图1 移动荷载匀速作用于简支梁
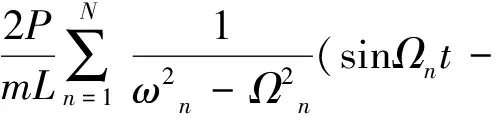
(1)
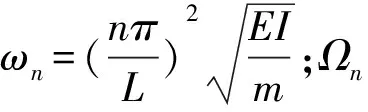
表达式(1)中前一项表示结构的强迫振动,后一项为结构的自由振动,当P速度趋于0时,vt=x1;式(1)可改写为
(2)
式中
P移动到x1处产生的挠度ys可表示为
(3)
从(2)、(3)式中可以看出,当试验作用的移动荷载速度无限趋于零时,所得到的位移值就会越趋近于结构静载时的位移值,该理论在连续梁桥同样适用[12]。为得到桥梁模型实际的静态位移影响线,只需控制荷载以接近零的速度匀速通过桥梁,所得到的影响线即为桥梁的准静态位移影响线。
1.2 建立模型
位移影响线是指某一截面的位移值随移动荷载位置的变化而变化。本文采用ANSYS有限元软件来模拟桥上行车时跨中产生的动力响应。建立单跨为20 m的三跨连续梁,梁截面高0.6 m,宽0.3 m,弹性模量为2.1×1011N/m2,泊松比为0.3,材料密度为7800 kg/m3,移动力为58860 N,连续梁每0.1 m为一个荷载步,打开瞬态效应,循环加载求解结果为动载效应下桥梁的位移时程曲线,将移动力换算为单位力,位移时程曲线即为桥梁的位移影响线。荷载以4种不同速度从桥的一端向另一端移动,其中速度极低的位移时程曲线称为桥梁的准静态影响线,桥梁中跨跨中节点的位移影响线见图2。

图2 不同速度下桥梁中跨跨中位移影响线
2 位移影响线识别方法
2.1 dbN小波变换法影响线识别
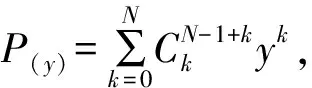
(4)
其中
(5)
式中:ω为频率,h为转换函数。
作用力分别以30 km/h、60 km/h和120 km/h的速度在三跨连续梁上移动,dbN法识别结果与准静态影响线数据对比见图3至图5。
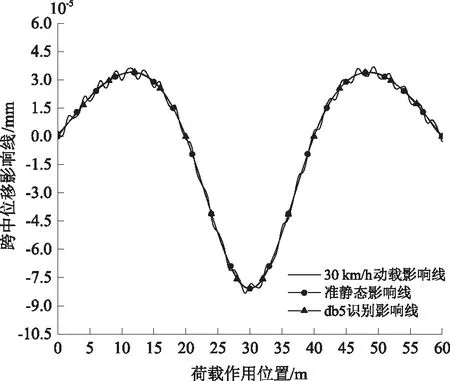
图3 v=30 km/h的动载影响线db5识别结果
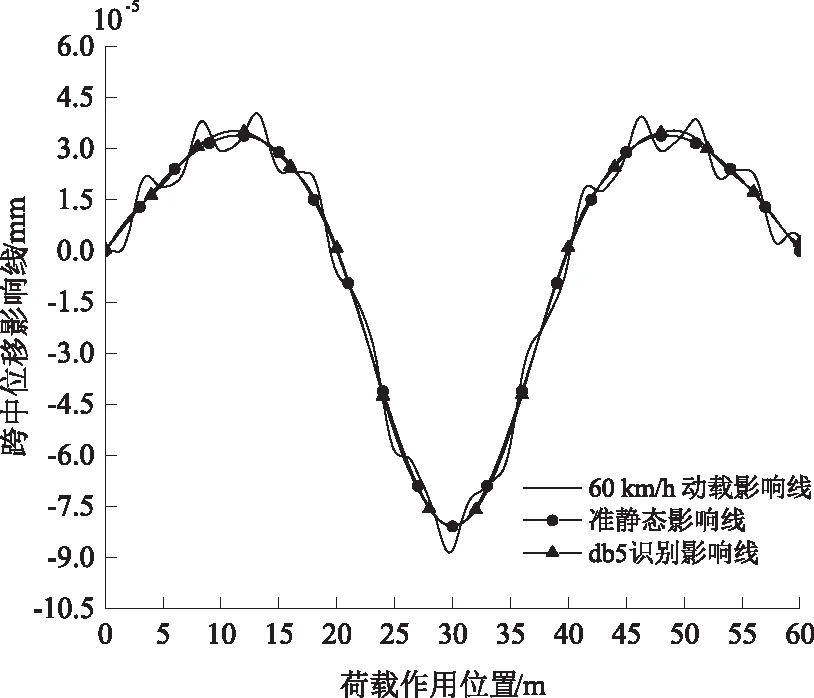
图4 v=60 km/h的动载影响线db5识别结果
从图3至图5可看出,随着荷载移动速度的增大,位移影响线识别结果会变差。当荷载速度为30 km/h时,识别的位移影响线与准静态影响线几乎重合,表明该速度下dbN法识别效果较好;荷载速度为60 km/h时,识别影响线在两边跨跨中附近出现微小偏差,且两边跨跨中附近的影响线数值大于准静态影响线;当荷载速度为120 km/h时,两边跨的识别的影响线与准静态影响线吻合程度较差。通过分析不同速度下的位移影响线识别结果,发现dbN小波变换法对三跨连续梁的中跨影响线极值点均具有较好的识别效果。
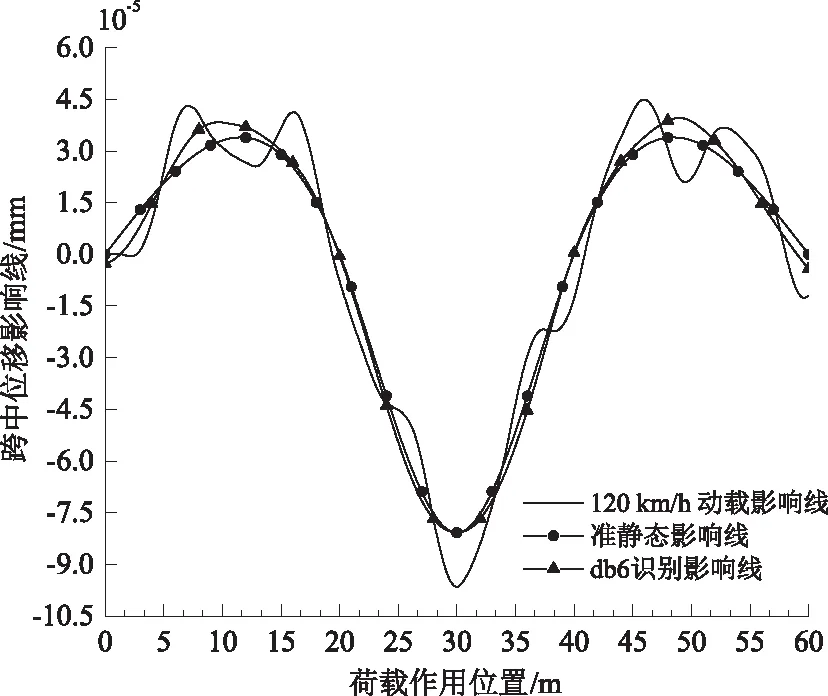
图5 v=120 km/h的动载影响线db6识别结果
2.2 经验模态分解法影响线识别
经验模态分解(Empirical Mode Decomposition,EMD)是将原始信号分解为若干本征模态函数(Intrinsic Mode Function,IMF),分解过程为取含动力响应的位移影响线上下极值点,分别绘出上下包络线,通过求均值拟合出均值包络线[15]。EMD分解模态严格遵循两个原则:(1)在待处理信号中,极值点与零点的数目相差不超过1;(2)上下包络线函数的均值为0。
EMD寻找IMF步骤如下所述:(1)输入原始信号y(t),寻找极大值点和极小值点;(2)用样条曲线绘制极大、极小值包络线emax(t)、emin(t);(3)求均值包络线,m(t)=(emax(t)+emin(t))/2;(4)原始信号减去平均值,h1(t)=y(t)-m(t);(5)建立新函数h1(t)代替y(t),重复1~4步获得hk(t),直到hk(t)满足IMF条件,定义IMF1(t)=hk(t),当重复迭代的本征模态函数的主要频率低于结构基频时,筛选终止;原始信号分解后的残差称为结构的静态响应。
由经验模态分解法识别桥梁准静态影响线的方法称为EMD法[16]。EMD法表达式为
f(t)=IMF1(t)+IMF2(t)+...+IMFn(t)+rn(t)
(6)
式中:rn(t)为原始信号的残差。
作用力分别以30 km/h、60 km/h和120 km/h的速度于三跨连续梁移动,EMD法识别结果与准静态影响线数据对比见图6至图8。
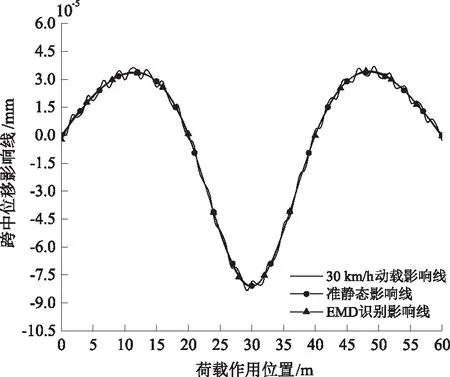
图6 v=30 km/h的动载影响线EMD识别结果

图7 v=60 km/h的动载影响线EMD识别结果
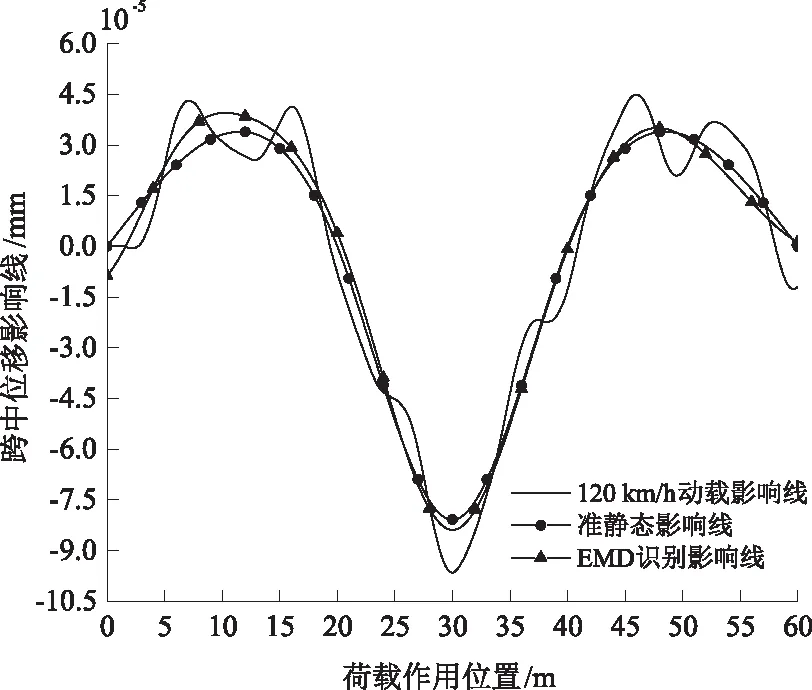
图8 v=120 km/h的动载影响线EMD识别结果
从图6至图8可看出,EMD法随着荷载移动速度的增大,位移影响线识别效果会变差。当荷载速度为30 km/h时,识别的影响线与准静态影响线吻合程度较高且几乎重合;荷载速度为60 km/h时,识别的位移影响线数值在中跨极值点处与准静态影响线吻合程度较高,但两边跨出现不同程度的误差;荷载速度为120 km/h时,识别的位移影响线与准静态影响线之间的误差较明显,在中跨极值点处识别的位移影响线数值明显大于准静态影响线,且两边跨的位移影响线与准静态影响线之间出现不同程度的误差;第一跨识别的位移影响线在准静态位移影响线上下波动程度明显大于第三跨。
3 误差指标及相关系数
3.1 误差指标
为定量评定dbN小波变换、EMD两种方法对位移影响线的识别效果,引入绝对误差指标Er,根据三跨连续梁的受力特点,桥梁跨中截面为控制截面,引入加权系数ωi,两边跨的位移值ωi取1,中跨的位移值ωi取2,从而对桥梁跨中截面进行加权。公式中的平方项是为了消除拟合后影响线与准静态影响线差后求和引起的误差,误差指标为
(7)
式中:i为节点编号;ωi为加权系数;ymi为拟合后的影响线数值;n为样本点个数;ysi为准静态影响线数值。
3.2 相关系数
通过对比两种方法的误差指标可判断两种方法对位移影响线识别效果,引入相关系数r,可判断拟合后的影响线与准静态影响线的相关程度,即拟合结果的可信度,r越趋近于1时,说明影响线识别的可信度越高,如公式(8)。
(8)
dbN、EMD两种方法的识别效果见表1。

表1 通过误差指标与相关系数分析影响线识别效果
从表1可知,两种方法的拟合效果都会随荷载移动速度增加而变差,但误差均小于2×10-12,相关系数值均接近1,说明两种方法均可有效识别桥梁位移影响线。荷载移动速度为30 km/h时,两种方法均有较好的拟合效果,拟合后的数据与准静态影响线相关程度最高,其中dbN小波变换方法拟合效果好于EMD法。
由于桥梁跨中的位移极大值更受到人们的关注,因此分别对比两种方法对桥梁中跨影响线极大值的识别效果(见表2)。
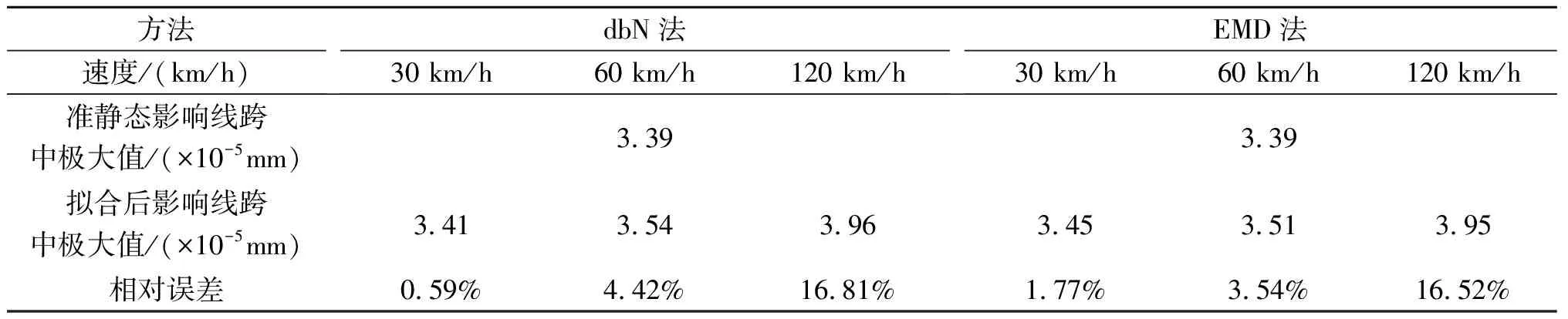
表2 三跨连续梁中跨影响线极大值识别效果对比
从表2可知,两种方法在桥梁中跨跨中位移影响线识别效果会随荷载移动速度的增加而变差。dbN小波变换法在移动荷载速度为30 km/h时识别效果优于EMD法,当移动速度达到60 km/h、120 km/h时,EMD法对桥梁跨中识别效果较好。
为进一步研究两种方法对含动力相应位移影响线识别效果,分别建立单跨20 m简支梁、单跨20 m的五跨连续梁,模型参数与移动力大小与本文1.2节中三跨连续梁模型分析条件相同,通过误差指标进一步分析,结果如表3所示。
由表3可知,当荷载移动速度小于30 km/h时,两种方法均可有效识别位移影响线,其误差均小于5×10-12,对含动力响应的位移影响线均有较好的识别效果;两种方法对于不同结构影响线识别结果的相关程度均在0.98以上。随着荷载移动速度增加,误差也相应增大;当桥梁结构为简支梁时,EMD方法识别效果比dbN方法识别效果好,当桥梁结构为连续梁时,dbN方法的识别效果优于EMD法。
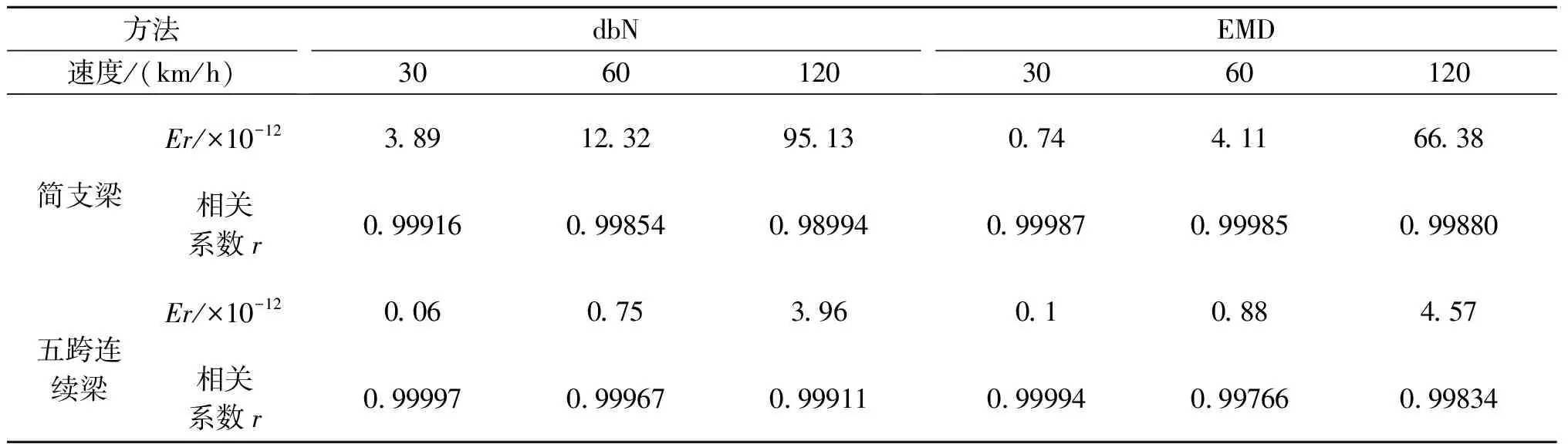
表3 不同结构跨中影响线识别效果对比
4 结论
(1)dbN、EMD两种方法在荷载移动速度较低的情况下,拟合后影响线与准静态影响线相关系数均在0.99以上,可有效识别含动力响应的位移影响线,随着荷载移动速度的增加,两种影响线识别方法效果均会变差。
(2)当桥梁结构为简支梁时,EMD方法识别位移影响线效果比dbN方法好,对于连续梁桥,dbN方法识别效果优于EMD法。
(3)因荷载移动速度的增大会导致影响线识别精度下降,故在实桥检测中应使加载车辆以较低的速度匀速通过桥梁。
综上所述,本文为简支梁桥与连续梁桥分别提出两种位移影响线识别方法,可为桥梁检测相关研究人员提供多种参考。
