Multi-Agent协商中风险偏好的影响研究

陈一真

(郑州大学商学院 河南 郑州 450001)

0 引言

随着全球化的快速发展，制造企业间的竞争也渐渐反映为供应链之间的竞争，而且制造企业的快速发展对制造企业供应链的上下游企业之间在数据共享和相互协作方面提出了更高的要求。如何提高制造企业供应链中各节点企业间的协商效率和协商成功率，对供应链协商中参与者的行为因素和规律的探索成为重要的研究方向。在许多供应链协商的研究中，研究者们都为协商参与者赋予风险偏好的特性或者在协商策略中设计一个学习机制来学习协商对手的风险偏好程度来提高协商效率或者使协商参与者获得更多的满意度。协商参与者的风险偏好的加入使协商过程更符合现实中的实际情况，论文以Multi-Agent技术下的制造企业供应链协商为例，利用基于贝叶斯学习的Agent协商模型对协商参与者风险偏好水平的影响进行研究，进而寻找其规律。

1 理论框架

在涉及供应链管理的协商中，供应链合作伙伴间通常基于交货期、质量、价格、数量等多指标问题进行协商，这些协商被描述为买方-卖方协商。多数研究者在研究协商时都将代理(Agent)和多代理系统(Multi-Agent System)技术应用其中，Agent技术起源于分布式人工智能(DAI)，Wooldridge认为每个Agent代表一个有目的的组件系统的自主行为的环境，以满足其预定义的目标[1]。多个Agent组成的系统被称为多代理系统(Multi-Agent System)，多代理系统的主要优势体现为社会性、自制性以及协作性，可以解决单个Agent不能解决的复杂问题。Braun和Kersten等人使用软件Agent代表供应链成员，实现了自动化买方-卖方协商[2]。同时，为了更好地符合人类协商的复杂性，增强Agent对环境的适应性，许多研究者都致力于在协商模型中引入了学习机制，将机器学习(Machine Learning)技术用于帮助Agent协商中。应用于代理协商中比较成熟的机器学习方法有：遗传算法、强化学习、贝叶斯学习、人工神经网络等[3]。其中，贝叶斯学习是一种比较经典的学习方法。学习过程包括利用贝叶斯规则中最近的证据和信息(如对方的还价)来更新假设的概率。概率最大的假设为学习主体提供了对手的模型，这有助于它在下一阶段的谈判中提出更好的报价。Zeng和Sycara提出了Bazaar，这是一个序列决策专门为电子商务设计的谈判模型。在该模型中，Agent使用贝叶斯方法学习对手的保留价格作为策略参数[4]。Faezeh等人提出了一种基于递归贝叶斯滤波的估计技术，使代理通过递归地实时学习协商对手偏好的模型参数，以方便在多参与者、多问题协商的背景下进行对手建模和学习，提高了协商的效率[5]。

在真实的协商过程中，不同的协商参与者面对相同协商议题, 采取的行动也不一样，因此，为了更符合现实中的协商过程，在研究Agent协商时通常考虑协商参与者在提议时的风险偏好程度或耐心程度，在协商过程中，Agent的类型会决定其使用什么样的协商策略, 从而对提议的取值、让步的幅度等决策产生直接的影响。武妍等将Agent分为激进型、缓和型和保守型，在协商中，可以通过把对方Agent的类型与自己的类型进行比较来估计对方Agent类型，从而调整自己的提议策略和战术[6]。张宏和何华灿提出了3种不同风险偏好类型Agent所采取的协商策略，在此基础上提出一个多Agent的协商算法,并结合具体实例给出不同偏好下Agent的组合对协商中协商成功率的影响[7]。李义华提出了一种基于多智能体的供应链虚拟企业买卖双方的出价策略协商算法，用下一步期望出价来确定各个协商主体的风险偏好参数，使代理协商过程更加贴近现实，同时讨论了不同类型协商Agent对协商轮次，出价序列和成交价格的影响[8]。

以上的研究内容为供应链Agent协商提供了良好的理论基础，但仍然存在不足之处，现存文献在Agent协商中考虑到实际协商中协商参与者的风险偏好程度，但对协商参与者风险偏好程度对协商过程的影响做出的分析都很有限，因此，本文拟运用一种基于贝叶斯学习方法的协商模型研究制造企业供应链代理协商中协商参与方的风险偏好对协商过程的影响，用于解决以上问题。

2 基于贝叶斯学习的制造企业供应链协商模型

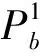
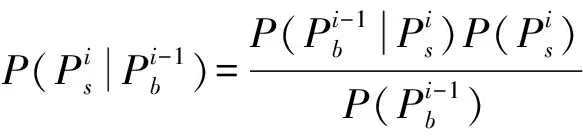
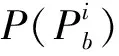
由条件概率公式可知

那么，带入贝叶斯公式以后可以得出后验概率

同理可得，对于制造企业，

先验概率是已知的，那么后验概率

(1)供应商的报价策略为

(2)制造企业的报价策略为

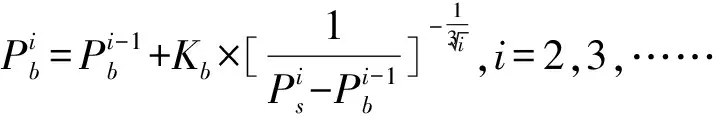
其中，i代表协商次数；Kb和Ks分别是制造企业和供应商的风险偏好参数，参数范围为区间(0,1)，参数越小，协商方偏好风险的程度就越小，在报价中越有耐心，反之，越偏好风险。

3 协商算例研究及风险偏好分析

3.1 协商次数的影响分析

当初始报价集合为[430,500]时，协商实例仿真的协商次数结果如表1所示。

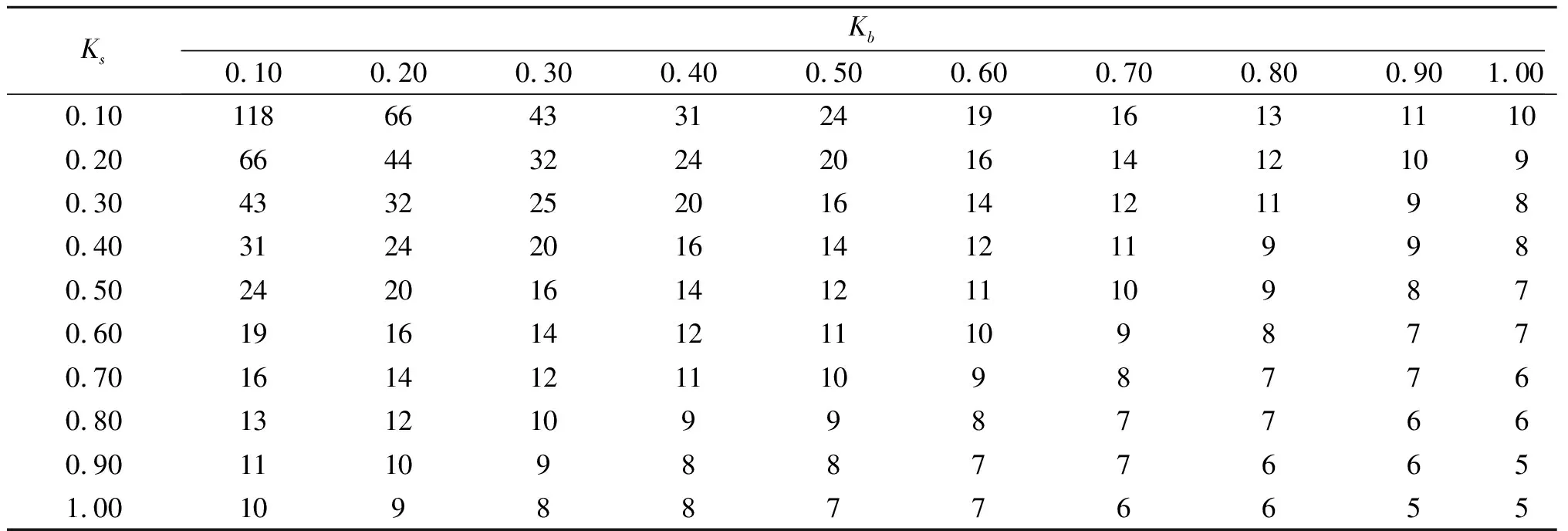
表1 协商次数对比汇总表

由表1可以发现，协商达成一致的次数随着协商双方风险偏好参数的增大而变小。当Kb保持不变时，协商次数T随着Ks的增大而减小，即供应商越偏好风险，耐心程度越低，协商次数将越少，更容易达成协商的一致意见。同时，对于制造企业越偏好风险，耐心程度越低，协商次数越少，达成协商的一致意见的速度更快，将具体协商过程绘制如图1所示。

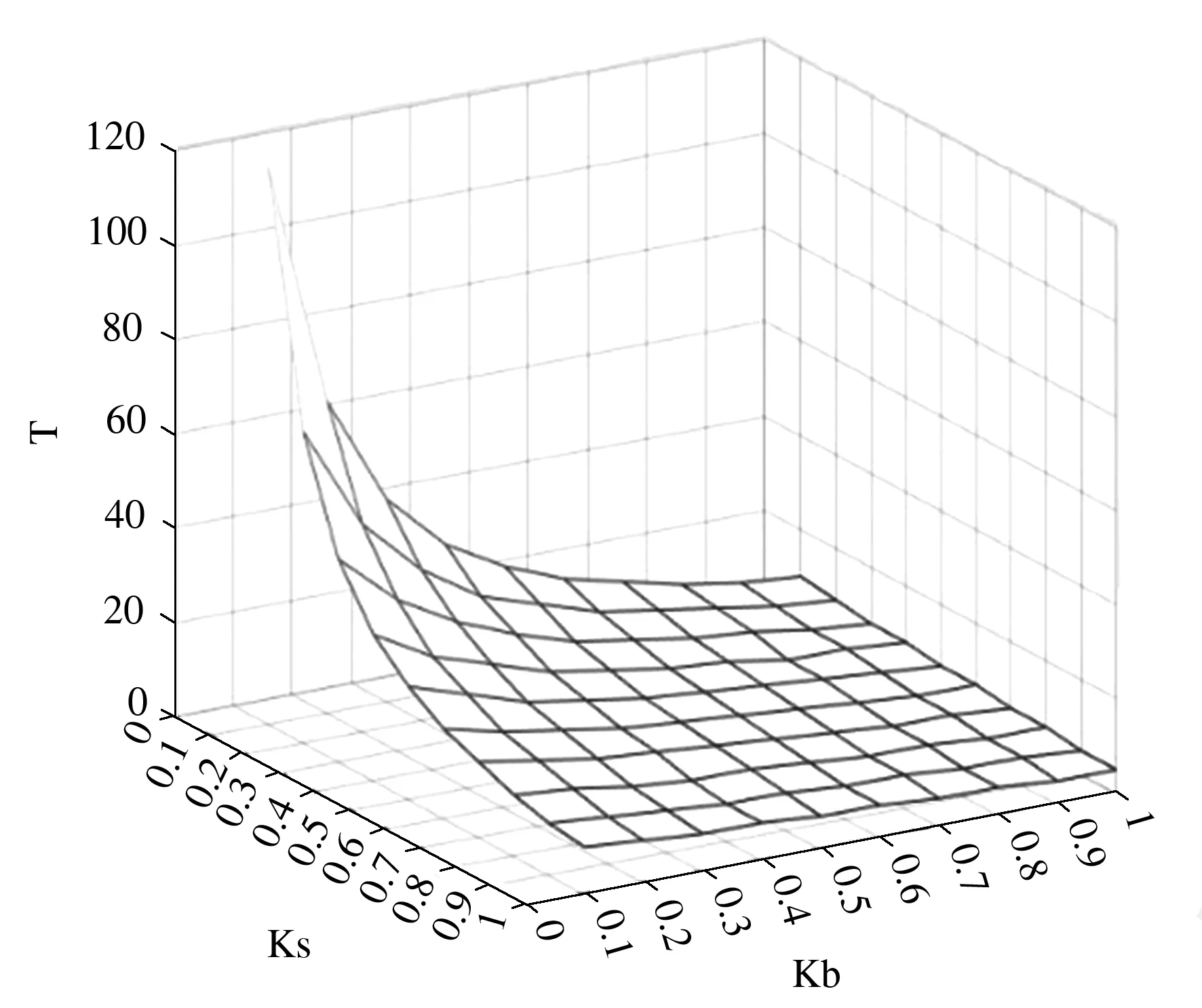
图1 不同风险偏好水平时协商次数三维图

在图1中当协商参与者的风险偏好系数均为0.1时，协商达成一致的次数最多，随着协商双方风险偏好系数的变大，协商次数都会变少。根据y-z面侧视图，不管Kb为何种水平，协商次数T都会随着Ks的增大而减小，但是随着Kb的增大，协商次数T随着Ks的增大而减小的趋势会变得越来越平缓，当Kb小于0.2时，协商次数T的变化呈现指数下降，而当Kb大于0.8之后，协商次数的变化基本成为一条水平的直线。同样，对于协商次数T随着Kb的变化也有相同的规律，协商次数T随着制造企业的风险偏好水平Kb的增大而减小的趋势会随着Ks的增大变得越来越平缓。

由此，可以看出，协商中的协商次数与协商参与者的风险偏好程度成反比，在协商中，任意一方风险偏好程度增加，协商效率都能够得到提升。协商参与者的风险偏好都达到最低值时，协商次数最多；反之，则协商次数最少，协商达成速度最快，效率最高。但当参与协商中某一方的风险偏好程度很高时，T几乎不会受到参与协商中另一方的风险偏好程度的影响；相对的，当参与协商中某一方的风险偏好程度很低时，协商次数将会强烈受到参与协商中另一方的风险偏好程度的影响，协商次数会随着另一方的风险偏好程度的减小而增加，一方的风险偏好程度越低，协商的次数受到另一方风险偏好程度的影响就越强烈。

3.2 成交价格的影响分析

初始报价集合为[430,500]时，协商实例仿真的成交价格结果如表2所示。

根据表2，成交价格会随着Kb的增大而增大，而随着Ks的增大而减小。当Kb保持不变时，成交价格P随着供应商的风险偏好参数Ks的增大而减小，即：供应商越偏好风险，耐心程度越低，成交价格就越小，越靠近制造企业的初始价格。同时，对于制造企业，制造企业越偏好风险，耐心程度越低，成交价格就越大，越靠近供应商的初始价格。将具体协商过程绘制如图2所示。

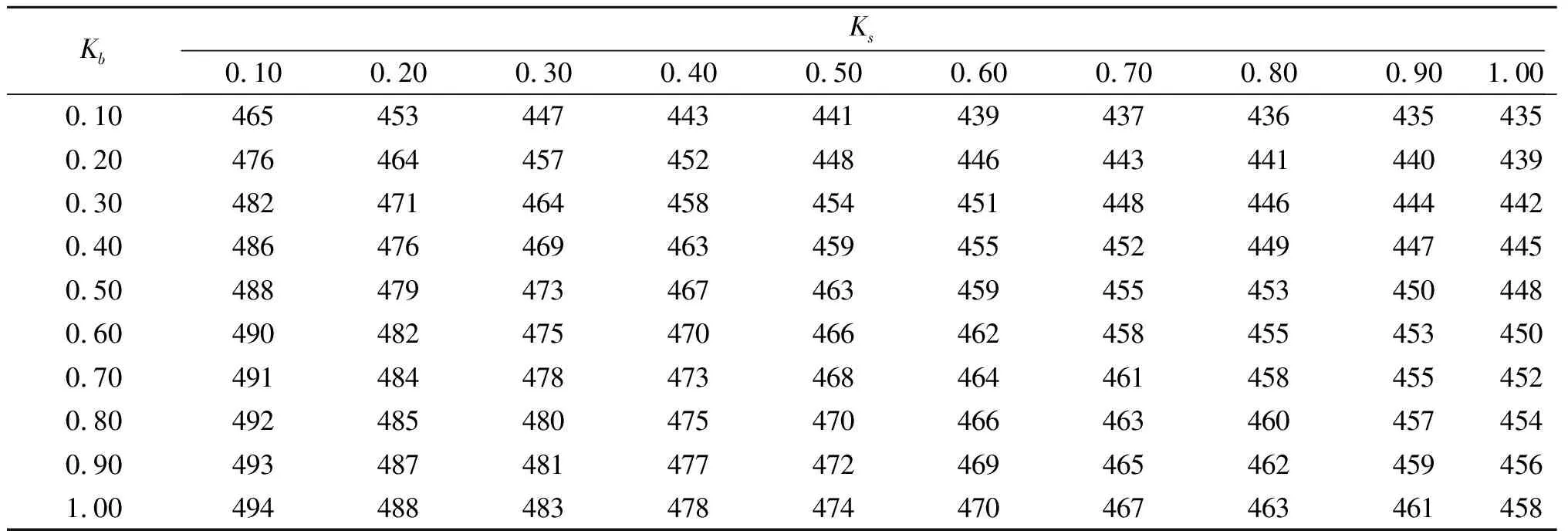
表2 成交价格对比汇总表

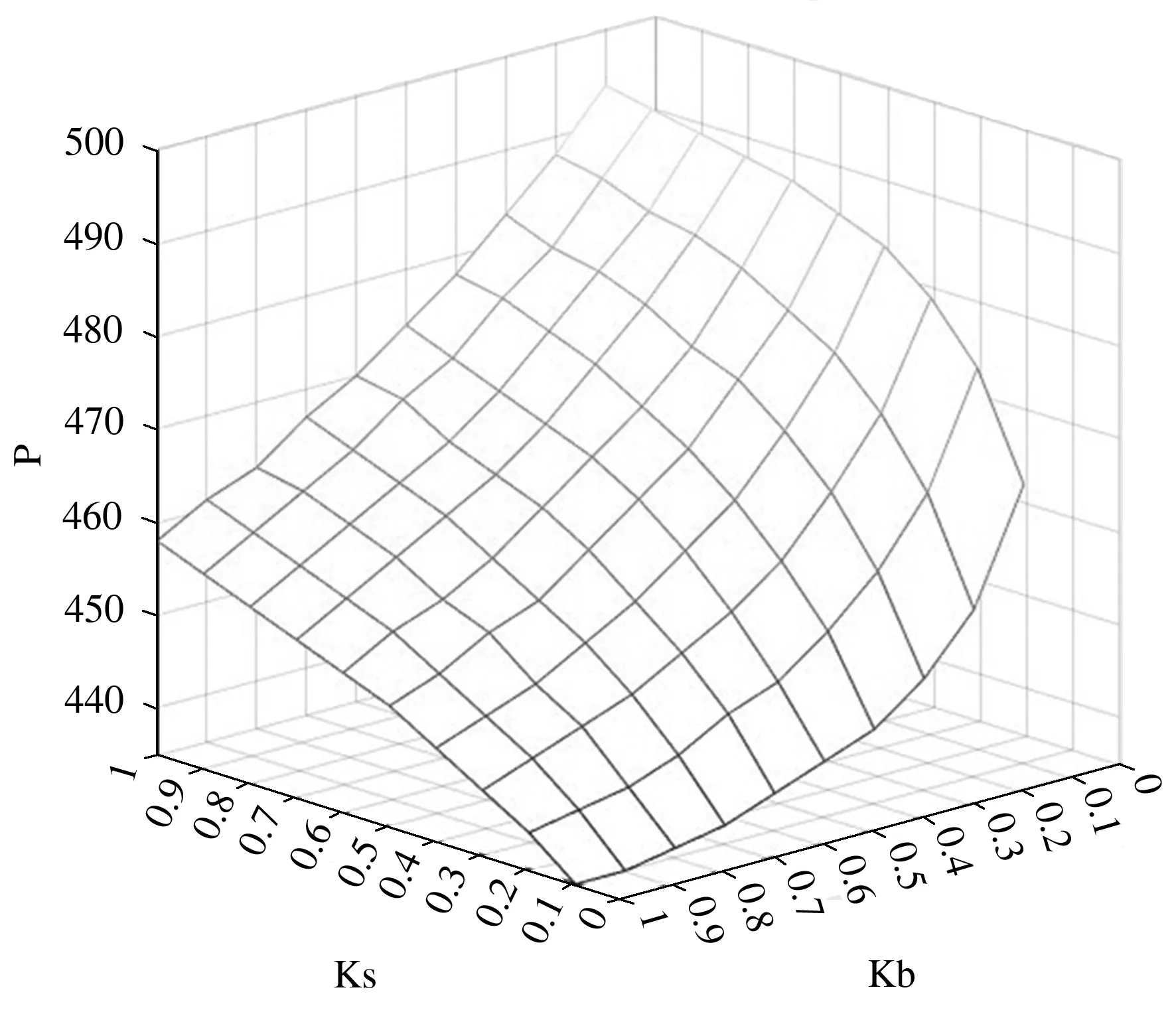
图2 不同风险偏好水平时成交价格三维图

4 结论

本文分别分析了协商中制造企业和供应商在不同风险偏好水平下的协商次数和最终成交价格的变化规律，有助于理解协商中不同协商参与者的行为规律，提升协商效率，增加协商参与者效用，对于协商参与者学习不同协商对手的协商策略也具有指导意义。

本研究只是关于复杂自动协商的初步成果，今后还应进一步对其改善，将此研究扩展到多边多协商议题的协商环境中，构建多边多议题的协商框架，对多边多议题的协商环境进行研究。