基于ECT技术的充填管道内固液两相流仿真方法研究

秦学斌 李明桥 申昱瞳 杨培娇 胡佳琛 刘 浪

(1.西安科技大学电气与控制工程学院,陕西 西安 710054;2.西安科技大学能源学院,陕西 西安 710054)

在矿产开采过程中会形成地下采空区,如果不及时充填,会造成地表沉降和塌陷,对矿山安全生产构成极大威胁。为了解决上述问题,较有效的思路是使用尾砂、胶结剂等各种充填材料,制成充填料浆,经过充填管道输送至采空区进行充填[1]。在输送过程中,充填材料中夹杂的废石和产生的结块会增加管道堵塞的可能性,如果不能及时发现问题,会发生爆管等严重的安全事故,造成较大的经济损失[2]。对充填管道进行检测,及时检测出管道的堵塞情况与堵塞结块大小,对于矿山充填的安全性具有重要意义。

目前,主要采用经验总结法[3]、层次分析法[4]、压力监测法[5]等对充填管道的堵塞情况进行监测与判断,该类方法实施困难、效率不高。近年来,已有学者利用电学层析成像对充填管道中的固—液两相流展开分析[6],但并没有对充填管道堵塞检测进行进一步研究。李桂臣等[6]采用超声检测方式对充填管道堵塞位置进行检测,但缺少对管道内部堵塞结块大小的判断。基于上述问题,本研究提出采用电容层析成像技术对充填管道进行检测,来判断是否存在堵塞结块以及管道横截面处结块的位置与大小。

电容层析成像(Electrical Capacitance Tomography,ECT)是一种用于可视化容器或管道内部的介电常数分布的技术[7-10]。ECT以其非侵入式、成本低等优势,越来越多地被应用于能源和化工等工业生产中[11-14]。现有的重建算法包括非迭代算法和迭代算法两大类。但由于ECT成像过程中“软场”特性和不适定问题,传统的非迭代与迭代算法成像精度低,已经不能满足工业生产的需要。此后,研究人员在重建算法的研究上开拓了新思路,如基于稀疏表示的重建技术[15]、软阈值迭代算法[16]等。近些年,随着神经网络技术的发展,其强大的数据拟合功能和特征提取能力使得研究人员不断地尝试将此技术引入到ECT的图像重建中。QUSSAI等[17]提出了一种基于前向问题的多层前馈组合神经网络,并使用Hopfield网络解决了逆问题。YE等[18]提出了基于稀疏表示的ECT图像重建算法,将介电常数分布由一个稀疏矩阵表示。LIU等[19]利用极限学习机建立了像素灰度值和电容的映射模型,并采用Landweber算法计算ELM的输出权重矩阵。FANG等[20]对用于介电常数分布预测的水平集方法进行了改进。ZHENG和PENG[21]提出了一种用于ECT图像重建的自动编码器。ZHU等[22]利用全连接网络模拟ECT中的正问题和反问题,搭建了解码器-编码器结构的介电常数预测网络,对介电常数分布进行预测并重建图像。YAN等[23]使用正则化解改进正交匹配追踪算法,提高了对ECT逆问题中不适定问题的适用性。

本研究将ECT技术应用于充填管道固液两相流检测,并提出适用于充填管道检测的基于极限学习机和卷积神经网络的ECT图像重建方法。该方法使用极限学习机构成ECT反问题的求解器,由卷积神经网络构成的编码器—解码器网络用于重建图像。该方法模型实现以测量电容数据作为输入值,并输出具有目标介质的图像。在研究中,数据集由电容值、介电常数值和真实分布图像构成。数据集主要包括沉积流、单核流、双核流和三核流,为了增加分布的多样性,在每一种流型中添加随机变量。本研究采用图像误差和相关系数来评估重建图像的精度。通过充填管道仿真试验,图像重建误差小于8%,对于检测充填管道堵塞问题具有重要意义。

1 基本原理

ECT图像重建技术可分为两部分,即正问题和反问题[24]。正问题是根据检测区域内介质的介电常数分布和敏感场的边界条件,求解各电极板的电容值。在敏感场内,根据拉普拉斯方程有下式成立:

式中,∇表示微分运算;ε为被测区域内介电常数分布;ϕ为被测区域内电势分布。

电场强度E是电势的负梯度,公式为

根据高斯定理和式(2),i—j极板间的感应电荷Qij可表示为

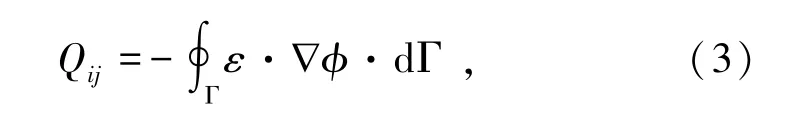
式中,Γ为包围极板的封闭曲面。

两极板间的电容值、场域内的电场强度和介电常数分布间存在如下关系,

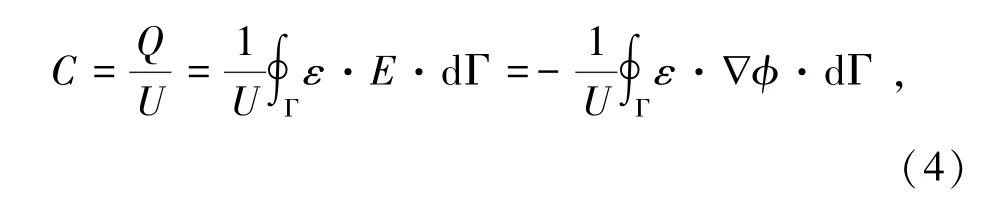
式中,C为两极板间的电容值;Q为检测极板上的电荷;U为两极板间的电势差。

已知检测区域内介电常数分布,求解各极板对间的电容,根据式(4)可得:

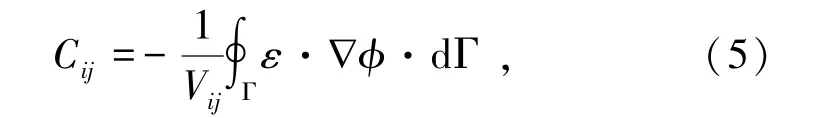
式中,Cij为第i和第j电极板间的电容值;Vij为第i和第j电极板间的激励电压。

ECT技术的反问题是根据敏感场分布和电容测量值求解被测区域内的介电常数分布。常用的简化方法是使用基于灵敏度模型的线性投影方法,基于此方法,反问题可表示为

式中,S表示被测区域的敏感场分布;g表示介电常数分布。

因此,若要得出介电常数分布,需要先求解敏感场分布。将传感器的敏感场区域剖分为若干个单元,在i—j极板对间,第σ单元的灵敏度值sij(σ)为

式中,Δε为介电常数分布变化;ΔCij为i—j极板对间由介电常数分布变化引起的电容值变化。

根据式(2)和式(7)可知,敏感场内点(x,y)处的灵敏度sij(x,y)为

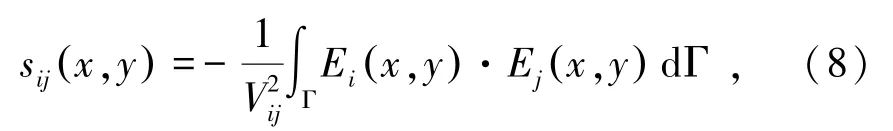
式中,Ei(x,y)表示当极板i施加激励电压Vij时点(x,y)处的电场强度。

根据式(8)获取敏感场分布时,会随着敏感场区域剖分精细程度的加大,计算量也会随之加大。且由于“软场”特性,敏感场分布随介质分布变化而变化,二者的非线性关系增加了反问题的求解难度。

2 ECT图像重建网络

2.1 极限学习机

利用前馈神经网络重建检测区域的归一化介电常数分布,为重建图像奠定基础。本研究使用极限学习机(Extreme Learning Machine,ELM)完成对单隐藏层前馈神经网络的训练,以模拟电容与介电常数值的映射关系。如图1(a)所示,网络的输入层为66×1的归一化电容数据,目标输出为1 681×1的归一化介电常数分布,将其整形为41×41的图像,以待后续的网络对其进行图像重建。

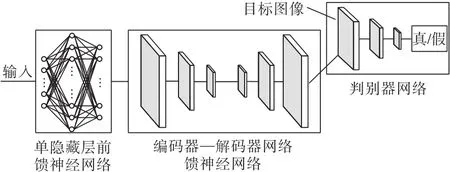
图1 ECT图像重建网络Fig.1 ECT image reconstruction network

ELM是一种快速学习算法,对于单隐层神经网络,ELM可以随机初始化输入权重和偏置并得到相应的输出权重。ELM保持了单隐藏层前馈神经网络的逼近能力,并且具有学习速度快、泛化能力强的优点[25]。隐藏层输出矩阵H可表示为

式中,x为网络输入矩阵;w为输入层节点的权重矩阵;b隐藏层节点的偏置矩阵;g·()为节点的激活函数。激活函数是为了让神经网络节点的输出适应电容数据和介电常数分布之间的非线性映射关系。本研究选用Sigmoid函数作为激活函数,公式为

有n个隐藏层节点的单隐层前馈神经网络的输出矩阵F为

式中,β为输出层的权重矩阵。训练过程可转化为求解一个线性系统,用矩阵可表示为

式中,T为期望输出矩阵。

即β的最优解为

式中,H+为隐藏层输出的 Moore-Penrose广义逆矩阵。

使用ELM的单隐藏层前馈神经网络训练可以重构电容数据和介电常数分布之间的复杂映射关系,Sigmoid激活函数在输出中引入非线性关系,使得网络比传统的线性化模型方法具有更好的数据拟合度。

2.2 图像预测网络

本研究搭建了基于卷积神经网络的自动编码器—解码器网络,用于预测介电常数值所对应的像素值,完成重建图像。图像预测网络架构由编码器—解码器网络和判别器网络组成,如图1(b)和图1(c)所示。

本研究中,由两层卷积层、两层反卷积层构成图像重建网络。该网络的输入值为图1(a)所示网络的输出经过整形得到的大小为41×41的图像,卷积层的卷积核尺寸为5×5,经过两次卷积操作得到编码器的输出值。解码器的作用是生成图像,将编码器的输出作为输入值,通过两次反卷积生成41×41的图像。

编码器—解码器网络重构的图像精度差,所以在自动编码器网络中引入了对抗的思路来优化网络的输出值。判别器网络需要对其输入值的来源做出判断,辨别此时的输入值来自解码器还是真实图像。判别器做出判断后,输出[0,1]区间的数值,数值越小,说明解码器生成的图像效果越差,数值越大,效果越好。当判别器无法判断出输入数据的来源时,停止训练。

在编码器—解码器网络中,采用smooth L1损失函数,其优点是对异常值的敏感度低,不易发生梯度爆炸的情况。图像预测网络的损失函数L为

式中,ti为目标像素值;yi为网络输出像素值。

梯度下降算法是机器学习中常用的优化算法。本研究使用小批量梯度下降法,每次更新从训练集中随机选择50个样本进行学习,在训练速度和训练效果之间取得平衡。

3 试验结果

3.1 数据集

本研究中用于训练ECT图像重建网络的仿真数据集是在COMSOL Multiphysics和MATLAB中建立的具有GUI的平台上生成的。每组数据集包含66元素的12电极的电容数据,1 681元素的介电常数分布及其对应的真实图像。

利用COMSOL软件建立12电极ECT二维有限元仿真模型,模拟充填管道的横截面,如图2所示。基于文献[7],在仿真模型中模拟矿山充填使用的尾砂胶结充填料浆[26],白色区域表示充填管道中的堵塞结块或废石,黑色区域表示正常流动的充填料浆。结块相对介电常数设置为5,充填料浆相对介电常数设置为2。

图2 ECT仿真模型Fig.2 ECT simulation model

数据集共有10 000组,包含4种流型,每种流型2 500组数据,并按2 000∶250∶250比例分为样本集、验证集和测试集。4种流型分别为单核流、双核流、三核流和沉积流,如图3所示。为了增加数据集的多样性,将随机变量添加到流型设置中。沉积流高度、核流中核半径和位置都为随机取值。

图3 ECT数据集流型Fig.3 Flow pattern of ECT data collection

3.2 充填管道仿真结果

使用测试集测试本研究网络的图像重建能力,重建效果如图4所示。为验证本研究方法的有效性,在图4中分别使用了 TSVD算法[27],ART算法[28],Newton-Raphson算法[29]和 Tikhonov算法[28]对于单核流、双核流、三核流和沉积流进行仿真试验。

图4 仿真试验结果Fig.4 Results of simulation experiment

在图4中,ART算法对沉积流的重建效果很差,且对核流重建时,仅可得知介质变化的大概位置,无法准确重建其大小。TSVD和Newton-Raphson算法对三核流的重建效果很不理想。使用上述4种经典算法进行重建图像时,出现变形和伪影的现象严重。进一步分析图4可知:本研究提出的ECT图像重建网络能够更好地显示图像的细节及边缘信息,图像质量得到提高,可以有效反映出大块废石和堵塞结块在管道横截面处的方位和大小。

本研究采用图像误差(Image Error,IE)和相关系数(Correlation Coefficient,CC)评估图像重建的质量,两者计算公式为

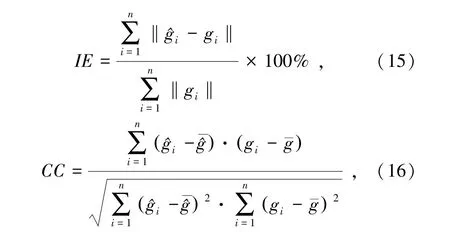
IE和CC通过计算重建图像和真实图像对应像素点的差异来衡量重建图像质量的优劣。IE越小,表示重建效果越好;反之,相关系数CC值越大,表示重建图像与真实图像的相关性越高,重建效果越好。测试结果的图像误差和相关系数见表1。

表1 不同流型的重建图像误差和相关系数Table 1 Reconstruction image errors and correlation coefficients of different flow patterns

由表1可知:本研究提出的图像重建网络对于简单流型的重建效果较好,如沉积流、单核流。在真实图像中,包含的元素越多,重建效果越差,如双核流和三核流,其中三核流的重建效果最差。

此外,进一步开展了充填管道仿真模型试验,获得的图像重建误差IE均小于8%,相关系数大于0.95。

在仿真条件下,本研究方法重建的图像质量较高,可以有效判断出充填管道检测横截面处的废石和堵塞结块所在的方位与大小。

4 结 论

(1)提出了利用极限学习机训练单隐层前馈网络解决反问题,并使用卷积神经网络重建图像的方法。

(2)将电容层析成像技术应用于矿山充填管道检测,通过对充填管道横截面固液两相流的可视化,可有效判断管道内的结块与堵塞情况。

(3)充填管道仿真试验结果表明,本研究方法可以有效判断管道内的结块与堵塞情况,具有一定的应用前景。不足之处在于未能利用电容层析成像系统对充填管道进行实际操作试验,如何实现对矿山充填管道的实时检测和更准确的成像效果仍是今后的研究重点。