快速公交多模式调度与沿线信号控制协同优化

2022-10-22韩印唐煜赵靖王经纬

铁道科学与工程学报 2022年9期

韩印，唐煜，赵靖，王经纬

(上海理工大学交通系统工程系，上海 200093)

随着社会经济的高速发展，交通需求日益增加，城市快速公交系统作为缓解城市交通拥堵问题的主要手段受到了很大的关注。我国现阶段的快速公交系统对运营调度与沿线交叉口信号控制分2 个阶段完成。但实质上，两者有着密切的联系，一方面，调度计划影响了公交达到交叉口的时刻，从而影响了交叉口信号控制的效果；另一方面，交叉口信号控制也在很大程度上决定了车辆在站点间的行驶时间，从而影响了调度计划的执行。因此，为了进一步提高快速公交运营效率，有必要对公交调度和交叉口信号控制进行协同优化。在公交方面，以往研究分为战略、技术、运营和控制等层次，对公交交通系统的线路和站点布置、发车频率设置、时刻表编制、车辆和驾驶员调度问题展开研究[1-4]。其中，在公交运营调度层面，早期主要关注线路的的发车频率，SCHÉELE 等[5-6]分别通过以乘客出行时间最小和乘客等待时间最少为目标来优化线路的发车间隔。近年来，主要研究从客流时空分布、组合调度、公交线网等方面提升公交调度效果。其中，客流时空分布方面，VERBAS 等[7-8]考虑客流量在时间和空间上的不稳定性，建立了以最小化候车时间为目标的车辆车头时距优化模型。组合调度方面，代存杰等[9]分析了多种车辆类型组合调度下的公交发车间隔和站点乘客需求，以乘客总候车时间最小和车辆平均满载率最大为目标，建立了该组合调度模式下的发车频率优化模型。陈维亚等[10]探究了有轨电车与常规公交运营组织协调策略。公交线网方面，卢小林等[11]从公交专用道和公交线路的角度考虑，构建了上层模型以最大化线路运营效率为目标，下层模型以最小化广义出行成本为目标的双层优化模型，寻找公交专用道和公交线网的组合优化方案。在交叉口信号控制方面，主要有3种优先策略：被动优先、主动优先和自适应优先。研究内容主要以交叉口为对象最小化公交延误，优化信号相位及配时等。在被动优先方面，马万经等[12]提出了基于车道的单点交叉口公交被动优先控制模型，模型考虑公交和社会车流延误，进行多目标优化。林丽等[13]考虑公交行驶过程中受到停靠站及自身行驶特性的影响，建立了基于双环结构的干线公交协调控制优化模型。窦慧丽等[14]建立了基于公交优先的单点交叉口车道信号协同配置模型，结果表明以交叉口通过总乘客数为优化目标，能保障交叉口同时获得更大的乘客和车辆通过能力。在主动优先方面，马万经等[15]以最大可能优先通行最优速度节能减排2个控制原则，建立了运行速度与优先控制方案的协调优化方法。TRUONG 等[16]提出了一种考虑了公交上下游交叉口优先和随机到达时间的公交信号优先模型。在实时优先方面，CHRISTOFA 等[17]考虑公交优先对社会车辆产生的消极影响，并以最小化消极影响为目标建立了交叉口信号控制模型。KOEHLER等[18]以快速公交为对象，采用迭代形式模拟快速公交运行过程，以最大化乘客出行延误减少量为目标实时集成控制车辆车头时距和公交信号优先，结合案例证明了集成控制的有效性。目前，分别针对公交调度和公交信号控制地研究均有较为丰硕的成果，但缺乏对两者的协同优化。由于快速公交拥有独立路权，行驶过程具有很强的可控性。本研究的意义在于进一步提升快速公交运行效率，减少乘客出行时间。创新点在于通过多模式调度和信号控制优化的组合，实现对发车时刻、停站策略和信号配时方案进行同步优化，从而在更大的可行域范围内获取最优解。

1 问题描述及解决思路

采用非固定的发车间隔以及大站车、区间车等多种调度模式是应对公交站点乘客客流需求不均衡性的有效方法，可提高快速公交系统的运营效率。同时，对快速公交线路沿线交叉口进行合理的信号配时，也是影响快速公交运营效率重要因素。且上述2个方面相互影响。以往的研究主要采用快速公交多模式调度优化(策略1)和交叉口信号控制优化(策略2)的方法来提升快速公交运营效率，然而2种优化策略都是单独进行的。

考虑到多模式公交调度会影响快速公交的交叉口到达时刻，从而影响快速公交通过交叉口的效率。同时，交叉口信号控制所产生的快速公交延误反过来又会影响多模式调度的执行效果，本文提出快速公交多模式调度与信号交叉口协同控制优化(策略3)的方法以提升快速公交系统的运营效率。各策略对比如图1 所示，其中“△”表示未优化，“●”表示优化。

2 模型建立

针对以上所提出的问题，采用数学规划方法进行建模。模型优化参数包括快速公交各班次的运行模式(M1ri和M2ri)、停站策略(δ1k和δ2k)、发车时刻(Tri1和Tri(m+1))以及沿线交叉口公交相位的绿灯开始时刻(Gjp)和绿灯时长(gjp)，这些参数构成了快速公交运行调度方案和沿线信号配时方案。模型首先以最小化总乘客出行时间为目标建立目标函数。基于递推思想，分别确定了快速公交车辆运行状态和公交乘客的出行状态。考虑到快速公交多模式调度和信号控制协同优化，模型分别对公交线路沿线交叉口信号状态、交叉口饱和度、快速公交多模式调度选择以及乘客站点候车时间进行了约束。下文分别对模型目标函数和约束条件进行介绍。

2.1 目标函数

本研究的目的在于提高快速公交的运行效率，对于公交系统而言，考虑到快速公交多模式调度和交叉口公交信号优先控制的关联性，快速公交在运行过程中的延误都能转化为乘客的候车时间和在车时间。因此，本研究目标函数主要从乘客角度考虑，以总乘客出行时间最小为优化目标，如式(1)所示。其中，乘客出行时间是指从乘客到达候车站点时刻到目的地站下车时刻的这段时间差值。

式中：r为车辆编号，r∈R；i为班次编号，i∈I，每辆车各自根据时间顺序编号，上行为奇数(从1开始)，下行为偶数(从2 开始)；s为节点编号，s∈S，包含交叉口节点J和公交站点K；k为公交站点编号，其中1 和m+1 分别为上下行始发站，k∈K；Arikk′为可乘上车辆r班次i的从k站到k′站所有乘客中的最晚到达时刻，s；qkk′(t)表示t时刻k站到k′站的乘客到达率函数，per/s；Tris为车辆r班次i到达节点s的时刻，s。

目标函数计算的关键是快速公交运行过程中车辆和乘客状态的确定，包括各班次车辆到达各节点的时刻以及各站点上下车乘客数量和乘客出行时间。本文基于递推思想，对快速公交和乘客的状态进行计算。

2.1.1 快速公交车辆状态的确定

对于快速公交车辆，将快速公交运营时经过的交叉口和站点看作节点，公交到达每个节点的时刻都可由其到达前一个节点的时刻递推得到，如式(2)所示。其中，快速公交在交叉口的延误可由式(3)计算，它取决于车辆到达交叉口时刻与绿灯相位的相对关系，由于快速公交拥有专用路权且流量相对较小，忽略排队的影响。快速公交在节点之间的行程时间，由于拥有专用路权，可直接按节点间距离与其设计车速的比值得到。快速公交的驻站时间与上下车乘客数量有关，可由式(4)计算。

式中：j为交叉口编号，j∈J；dris为车辆r班次i在交叉口j的延误，s；ds为节点s-1 与节点s间距，m；v为快速公交车速，m/s。

式中：Cj为交叉口j信号周期，s；Gjp为优化后交叉口j信号相位p的绿灯开始时刻，s；gjp为优化后交叉口j信号相位p的绿灯时长；p为交叉口信号相位编号，p=1 表示公交流向相位，p=2 表示协调信号相位编号。

式中：lrik为车辆r班次i在k站的驻站时间，s；Orik为车辆r班次i在k站的上客数，per；to为乘客上车所需时长，s；Drik为车辆r班次i在k站的下客数，per；td为乘客下车所需时长，s；ψ为车辆进站减速和出站加速所花费的时间，s；δ1k为大站车在k站是否停靠，1-停靠，0-不停靠；δ2k为区间车在k站是否停靠，1-停靠，0-不停靠。

2.1.2 乘客状态的确定

研究假设乘客到达率已知，对于任意从k站到k′站的上车乘客数量可由式(5)计算。其计算的关键在于确定从k站到k′站的所有乘客中哪些乘客可以上车，即确定按先到先服务的原则上车乘客的最晚到达时刻，计算中需要考虑公交的多模式行车计划和车辆容量限制。其中，对于大站车和区间车，存在车辆在某站点不停靠以及乘客目的地不在车辆服务范围的情况，因此应满足式(6)约束。

式中：r′i′为在车辆r班次i之前上一辆经过k站的车辆和班次编号；m为站点数。

式中：M1ri为车辆r班次i是否为大站车，1-是，0-否；M2ri为车辆r班次i为区间车，1-是，0-否。

在正常情况下，所有在i班次车服务范围内的乘客应都能上车，但考虑车辆容量限制，存在上车需求人数大于车内剩余容量的情况，因此应满足式(7)约束，式中剩余容量可由式(8)计算得到。在k站下车乘客数量为之前各站点上车的乘客中需要在此站下车的乘客累加得到，可由式(9)计算。此外，根据先到先服务的原则，所有目的地的上车乘客最晚到达时刻应相同，即满足式(10)约束。

式中：Urik为车辆r班次i在k-1 站到k站间的路段上的剩余容量，per；Orikk′为车辆r班次i上从k站到k′站的乘客数，per。

2.2 约束条件

2.2.1 交叉口信号控制约束

本文的优化目标是提高快速公交的运行效率，但在对沿线交叉口信号配时进行调整时，需要考虑社会车辆的约束。根据现状交叉口控制的不同情况，建立不同的约束条件。

情况1：交叉口处于干线协调控制系统中，公交相位与协调信号方向相同。为了不破坏原有社会车辆的线协调控制，优化后的公交信号方案应在时间上包含原有信号，即满足式(11)和式(12)约束。

情况2：交叉口处于干线协调控制系统中，公交相位与干线协调信号方向不相同。此时，同样为了不破坏原有社会车辆的线协调控制，应不改变社会车辆线协调方向的绿灯开始时刻和持续时长，即满足式(13)和式(14)约束。

情况3：交叉口属于单点控制。此时，公交流向所在相位的绿灯开始时刻和持续时长都可以调整，其余相位的绿灯时长按照原方案等比例调整，即满足式(15)约束。

式中：Ig为绿灯间隔时间，s。

2.2.2 交叉口饱和度约束

快速公交信号优先可能对交叉口相交道路的通行能力产生负面影响，因此需要设置交叉口饱和度约束，保障相交道路的服务水平满足基本要求，并且当初始饱和度已超过该阈值时，要求其饱和度不进一步增加，满足式(16)约束。

式中：Qjp为交叉口j信号相位p的车流量，veh/h；Q′jp为交叉口j信号相位p的饱和流量，veh/h；xmax为交叉口饱和度最大值阈值。

2.2.3 快速公交调度模式选择约束

不同运营模式应有不同的停站策略。全程车的停站策略为全部停站；大站车的停站策略为除在首末站不能跳站外，其余各站均可跳站，满足式(17)约束；区间车的停站策略为在上行(下行)某区间连续停站，上行(下行)其余站点均不停站，满足式(18)和式(19)约束。

式中：m1和m2分别为上、下行的站点数量。

考虑到不同运营模式的特点，如同一辆车在不同班次可以是全程车和大站车，但如果是区间车，则只能是区间车，满足式(20)和式(21)约束。

式中：M0ri为车辆r班次i为全程车，1-是，0-否。

快速公交在完成一次单线任务到达终点站后需休息调整，上下行休车时间满足式(22)和式(23)约束。

式中：τmin为最小休车时间。

2.2.4 乘客候车时间约束

乘客候车时间应小于最大值约束，如式(24)所示。根据《公共汽车和电车客运服务规范》，候车时间最大值取8 min。

wrikk'=Trik-Ar'i'kk'≤8， ∀r∈R;i，i'∈I;k，k'∈K(24)

式中：wrikk′为车辆r班次i上从k站到k′站的乘客的候车时间。

3 案例分析

本文提出的问题被描述为非线性规划，其中决策变量分为公交调度和信号控制2个方面，在公交方面为各个模式的停站方案、每辆公交的运营模式以及发车时刻；在信号控制方面为各个交叉口的公交流向相位的绿灯开始时刻和绿灯时长。算法决策变量规模为(发车班次数×2+站点数×2+交叉口数量×2)个，采用遗传算法进行求解，关键步骤如下所示。

步骤1：确定染色体编码方式，适应度函数、交叉概率和变异概率等，初始化种群。种群规模取100，交叉概率取0.7，变异概率取0.2，最大迭代次数取100。

步骤2：判断染色体的适应度值是否符合优化准则。若符合，跳出步骤，输出最优个体，否则，继续下一步骤。

步骤3：锦标赛选择策略。常用的选择策略有轮盘赌选择和锦标赛选择，因为锦标赛选择每次选择最好的个体进入子代种群，故具有很强的可通用性。

步骤4：用父母染色体进行交叉，生成子代并对子代染色体进行变异。

步骤5：产生新一代种群，返回步骤2，直到个体连续迭代改善值小于10-4或达到最大迭代次数。

下文通过算例，将本文所提出的公交多模式调度与信号控制协同优化策略(“多模式+信号”)与仅采用公交多模式调度优化策略(“多模式”)、仅采用信号控制优化策略(“信号”)以及不采用任何优化策略进行对比，验证模型效益。

3.1 输入条件

以某公交线路为算例，公交上下行沿途设置24 个节点，其中公交站点14 个，交叉口10 个，公交站点站间距离为500 m，如图2 所示。研究时段为1 h，根据OD需求的不同，设计了2种工况，如表1 所示(上下行需求对称)。站点乘客上下车速度为3 s/per。公交车辆方面，线路上下行各配车6辆，每台车辆最大载客量为72 人，公交在节点间的行驶车速为8 m/s。最小和最大发车间隔分别为120 s 和480 s，其中常规运营调度下的发车间隔取360 s。公交车辆运营时，车辆若停靠站点，进出站损失时间取20 s。信号配时方面，交叉口信号周期为120 s，公交流向相位绿灯起始时间为信号周期第30 s，公交流向信号绿灯时长为30 s。

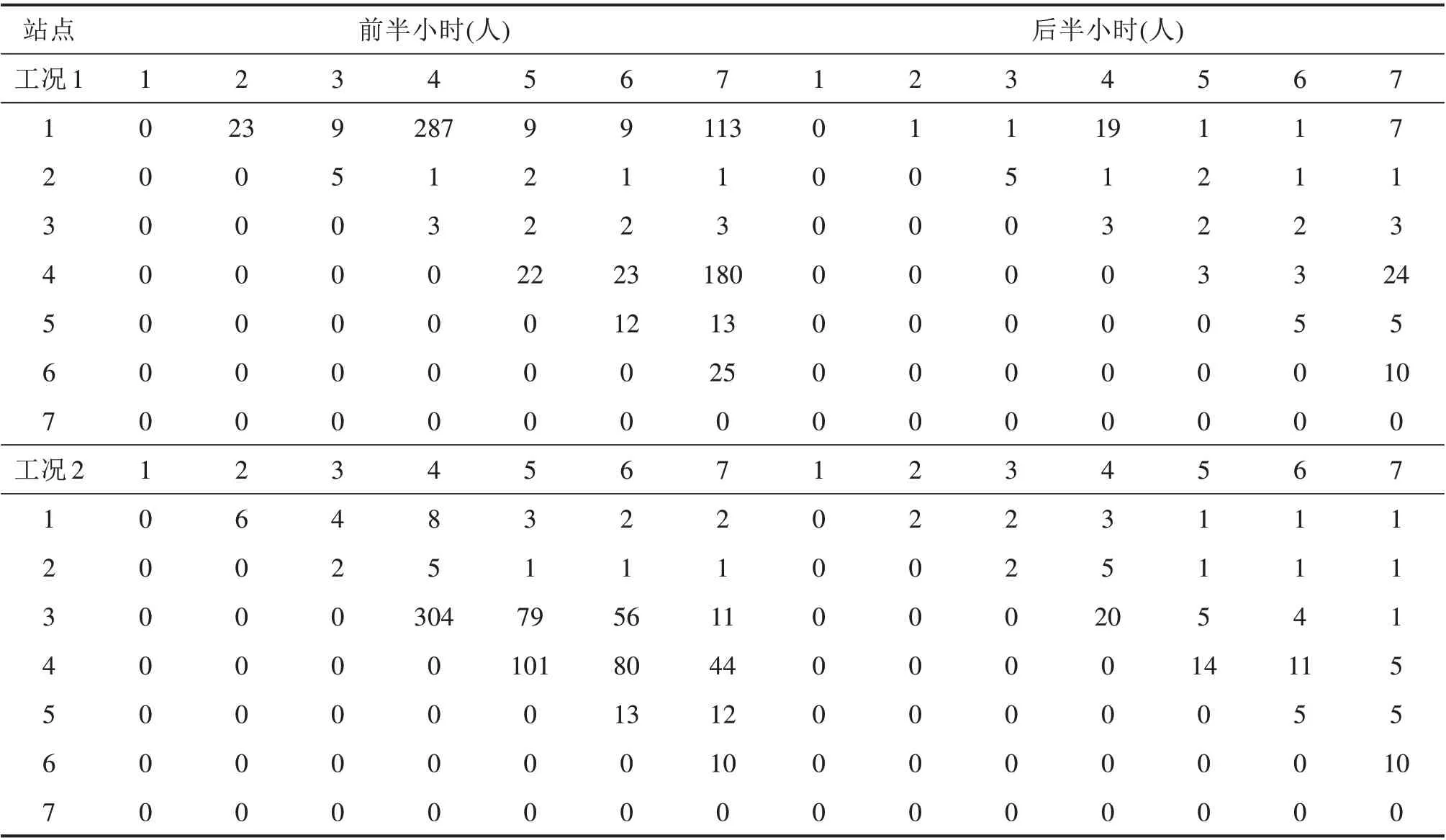
表1 乘客OD分布矩阵Table 1 OD distribution matrix of passengers

3.2 优化结果对比

根据求解结果，得到不同策略下的停站方案和公交运营时空图。由于篇幅所限，仅展示“多模式+信号”策略的结果，如图3～4所示。

不同策略下的公交服务指标结果如表2 所示。对比表中相同工况下不同策略间的各项指标结果发现：在工况1下，“多模式+信号”策略较单独使用“信号”策略和“多模式”策略，乘客总出行时间分别减少7.54%和21.06%，车辆交叉口延误分别减少13.94%和48.25%。在工况2 下，“多模式+信号”策略较单独使用“信号”策略和“多模式”策略，乘客总出行时间分别减少7.54%和15.12%，车辆交叉口延误分别减少23.67% 和43.02%。因此可以看出“多模式+信号”策略在2种工况下均为最优策略，常规策略在2种工况下均为最差策略。

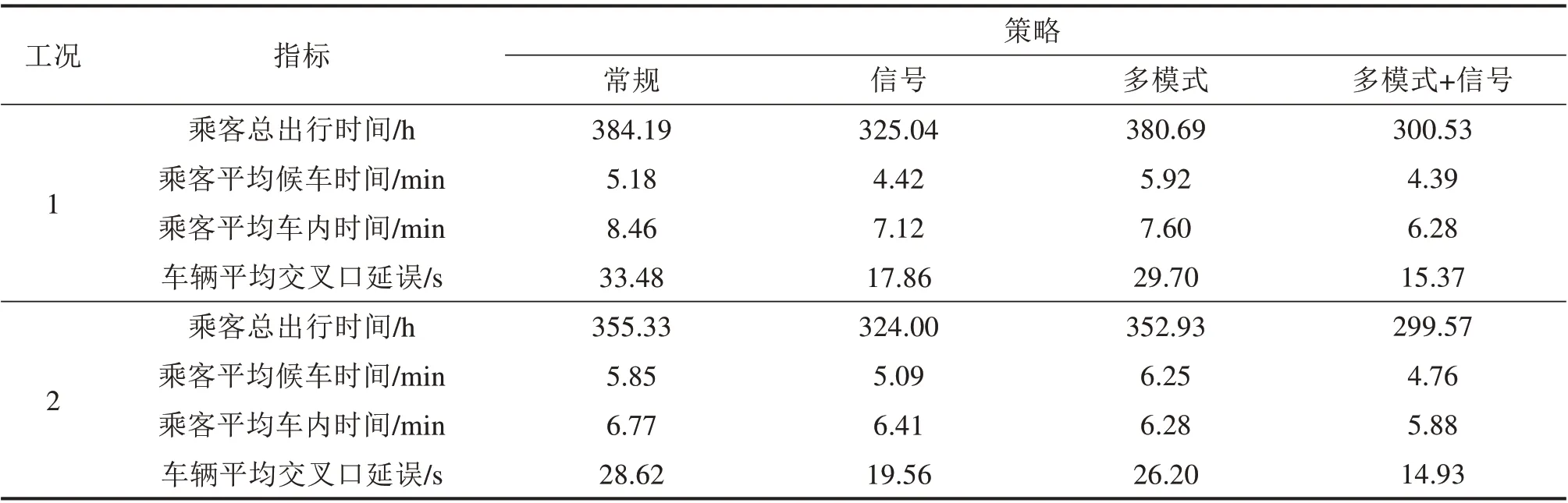
表2 不同策略下公交服务水平Table 2 Level of service comparison among various strategies

本文提出的“多模式+信号”策略在不同工况下都有较好的表现。大站车和区间车的停站策略均符合该工况下的乘客主要流量。通过调整发车间隔和将全程车调整为大站车或区间车等公交调度策略，确保了在主要客流段有不同模式的车辆进行服务并且服务车辆的载客数量基本相同，在客流突变的情况下也不会产生大量因无法及时上车而被滞留到后续车辆的乘客。通过信号控制优化，确保了公交车辆在交叉口的延误显著减少。因此将公交调度和信号控制结合能在减少乘客候车时间的情况下同时减少车辆在交叉口的延误，减少车辆串车情况，提高车辆的运营效率。