面向交叉口通行轨迹离散性的交通流模型参数标定方法
2022-10-22殷宇婷赵靖
殷宇婷,赵靖
(上海理工大学 交通系统工程系,上海 200093)
交叉口是城市道路的重要组成部分。不同于路段有较为明确的车道划分,交叉口内部无结构化车道,且驾驶人行为也各有不同,这使得车流通行轨迹离散化。然而,如何模拟车流轨迹离散化现象仍是一个挑战,本研究基于交通流模型,探寻能描述轨迹离散的驾驶人行为参数拟合方法。交通流模型参数取值对于模拟结果的真实性有很大影响,现有的参数标定方法主要有固定值法、边际分布法、多变量分布法。固定值法是参数取值最为常用的方法。BONSALL 等[1]整理了不同交通流模型的主要参数取值方法,都是通过假设、理论估计或观察得到,通过仿真验证了参数选取对于模型结果的重要性。LUSPAY 等[2]建立了高速公路交通流模型并通过公式推导确定了模型的参数。在固定值法的使用过程中,主要采用遗传算法对参数进行标定,选择最优参数[3-7]。相较于固定值法,边际分布法能够描述参数的分布情况。马国胜等[8]在建立两相位交叉口左转交通流冲突延误改进模型时,用负指数分布来描述车头时距。HENCLEWOOD 等[9]利用蒙特卡洛算法生成随机参数集,并使用均匀分布选择参数值的方法来提高微观交通仿真模型的精度。SARKAR 等[10]利用最大似然估计法拟合参数的边际分布,进行交通流仿真。MIKHAILOV 等[11]用Erlang 分布来拟合车头时距。研究发现,交通流参数之间存在一定的相关性。KIM等[12]验证了参数之间的相关性,并用多元正态分布的方法来拟合Gipps 模型、Helly 模型和IDM 模型中的参数组合。KABIR 等[13]建立了随机参数负二项式模型来评价交通信号性能对城市道路信号交叉口碰撞频率的影响,根据拟合优度统计信息和一般模型性能比较相关和不相关的随机参数负二项式模型,得出相关的随机参数负二项式模型能解释随机参数估计值之间的复杂相关性。虽然目前对交通流模型参数拟合方法有着丰富的研究,但多集中于路段,缺少针对交叉口车流通行轨迹离散现象的交通流参数拟合方法。现有的仿真软件对于交叉口仍采用与路段相同的基于车道的方法,无法体现通行轨迹离散现象。因此,有必要针对交叉口通行轨迹离散性建立交通流模型参数拟合方法。微观交通流模型是模拟车流轨迹的方法,主要可分为4 类:跟驰/换道模型[14-15]、元胞自动机模型[16-18]、社会力模型[19-20]和最优控制模型[21]。ZHAO 等[21]基于最优控制理论提出了一种新的交叉口二维车辆轨迹规划模型,可反映驾驶人包括转向和加减速的驾驶行为。该模型相较于其他3类模型,对交叉口车辆轨迹的可解释性更强,有利于本文研究交叉口通行轨迹离散性。因此,本文将基于该模型进行研究。以往研究显示驾驶行为具有不同类别,同时又具有离散性,难以用一种分布关系来描述,因此本文提出采用基于聚类的多变量分布法对参数进行拟合,先将参数分为不同的类别,再分别进行参数拟合,这样能够更精准地描述参数特征,从而更好地描述交叉口仿真车流轨迹的离散性。本文分为以下几个部分:第1 节介绍通行轨迹模型,第2 节介绍调查数据以及单个驾驶人行为参数标定结果,第3节提出驾驶人行为参数标定方法,第4节检验模型的准确性,最后总结研究结论及未来研究方向。
1 轨迹模型及驾驶人行为参数介绍
1.1 通行轨迹模型
本文采用ZHAO等[21]建立的通行轨迹模型,其主要思想为:通过求解下述最优控制模型,优化车辆转角和加减速,生成车辆运行轨迹。以车辆总通行成本最小化为目标,以车辆转角和加减速为控制变量,并考虑车辆转角、速度和加速度约束。
1) 状态函数。模型将车辆运动状态X(包括位置、转角和速率)定义为车辆行驶距离s的函数,车辆起始状态X0和终端状态XD为输入参数。
式中:X表示车辆的状态;x和y表示位置的平面坐标,m;θ表示转角,rad;p表示速度的倒数,s/m。
2) 动态系统。车辆的运动方程如式(2)所示。
3) 成本函数。构成决策通行轨迹的成本函数主要考虑通行时间和舒适性(包括横向加速度二次函数和纵向加速度二次函数),如式(3)所示。
式中:γ1,γ2和γ3是各成本的相对权重;ac表示车辆横向加速度,m/s2;al表示车辆纵向加速度,m/s2。
4) 约束条件。模型的约束条件包括,运行速度、运行曲率和加速度都在车辆运行允许范围内。
式中:vmax和vmin分别表示车辆的最大和最小速度,m/s。rmin表示车辆最小转弯半径,m。αmin和αmax分别表示加速度控制变量的最小值和最大值,s/m2。
1.2 驾驶人行为参数
上述模型能够真实模拟驾驶人的驾驶行为(包括转动方向盘,踩刹车和踩油门)。模型中驾驶员行为参数由参数γ1,γ2和γ3体现。其中,γ1为时间成本的相对权重,可以反映驾驶人对于时间成本的重视程度,γ2和γ3分别为横向加减速成本和纵向加减速成本,可以反映驾驶人对于舒适度的重视程度,这3个参数可以用于描述驾驶人行为,需要对其进行标定。总体的标定流程如图1所示。
2 调查与单个驾驶人行为参数标定
2.1 数据调查
选取上海市有左转保护相位的5个信号交叉口作为调查地点,从中筛选出不受其他车辆干扰的直行车辆和左转车辆数据用于研究。选取的5个交叉口分别为:扬泰路-镇泰路交叉口(编号1)、友谊路-铁力路交叉口(编号2)、祖冲之路-高斯路交叉口(编号3)、桃林路-灵山路交叉口(编号4)和高科西路-张东路交叉口(编号5)。采用无人机拍摄视频的方法采集交叉口早高峰时段的车辆数据,通过图像识别技术获取视频中每1/24 s车辆几何中心位置,得到车辆高精度通行轨迹,如图2所示。在后文分析中,1,2,3,4 号交叉口将用于驾驶人行为参数标定,5 号交叉口将用于驾驶人行为参数验证。
2.2 单个驾驶人行为参数标定
首先需要对各辆车的驾驶人行为参数进行标定。模型有γ1,γ2,γ3这3个参数,分别表示3部分通行成本的权重。由于这3个权重是相对的,自由度为2,因此可以将其中任意一个定为1,并标定剩余的2个来反映不同驾驶员的差异性。不失一般性,将γ1固定为1。
具体的标定流程如下。
第1 步:设置初始值。导入实际车辆轨迹数据,并确定初始状态参数[x0,y0,θ0,p0],终端状态参数[xD,yD,θD],加速度范围为-5 ~5 m/s2,最小转弯半径取5 m。
第2步:规划最优轨迹。利用通行轨迹模型根据设定的驾驶员参数来规划轨迹。
第3步:适应度计算。计算规划轨迹与实际轨迹对应点的误差平均值f。
其中,(xi,yi)为规划轨迹坐标点,(x0i,y0i)为实际轨迹的坐标点,n为坐标点的个数。
第4 步:迭代条件。比较前后2 次迭代的适应度f,利用序列二次规划算法寻找下一组γ2,γ3的值,回到第2步。
第5 步:终止条件。直到前后2 次迭代的适应度之差小于ξ(设为0.001)时,迭代停止。
第6步:结果输出。
以图3为例,图中实线为实际轨迹,虚线为规划轨迹。直观地,规划轨迹较好地拟合了实际轨迹,此时得到的γ2和γ3分别为0.022和0.026。从数值上看,规划数据与实际数据之间的平均误差为0.225 m,误差较小。
从1,2,3 和4 号交叉口共得到400 组驾驶人行为参数,平均误差为0.67 m,4 个交叉口各自的平均误差分别为0.79,0.86,0.50 和0.59 m,标准误差分别为0.51,0.43,0.35 和0.39 m。进而对其进行相关性分析。通过多元方差分析,如表1 所示,不同交叉口与驾驶人行为参数差异性不显著,转向对于γ2的差异性不显著,而对于γ3表现出显著的差异性。进一步分析转向的影响,如表2 所示,对于γ2,转向之间没有显著的差异性;对于γ3,左转和直行、右转和直行之间差异性明显。
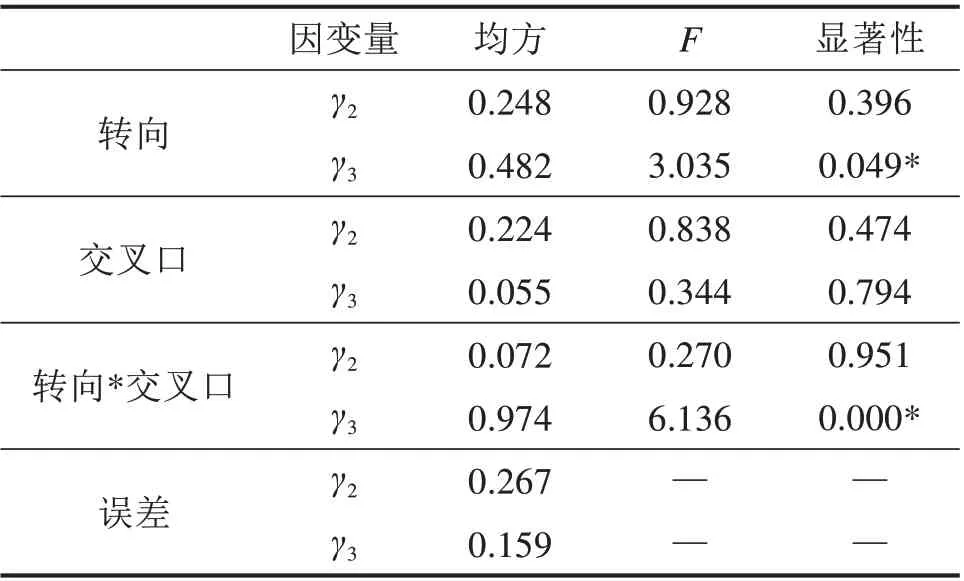
表1 交叉口与转向对于驾驶行为参数差异性检验Table 1 Difference analysis of intersection type and movement for driving behavior parameters
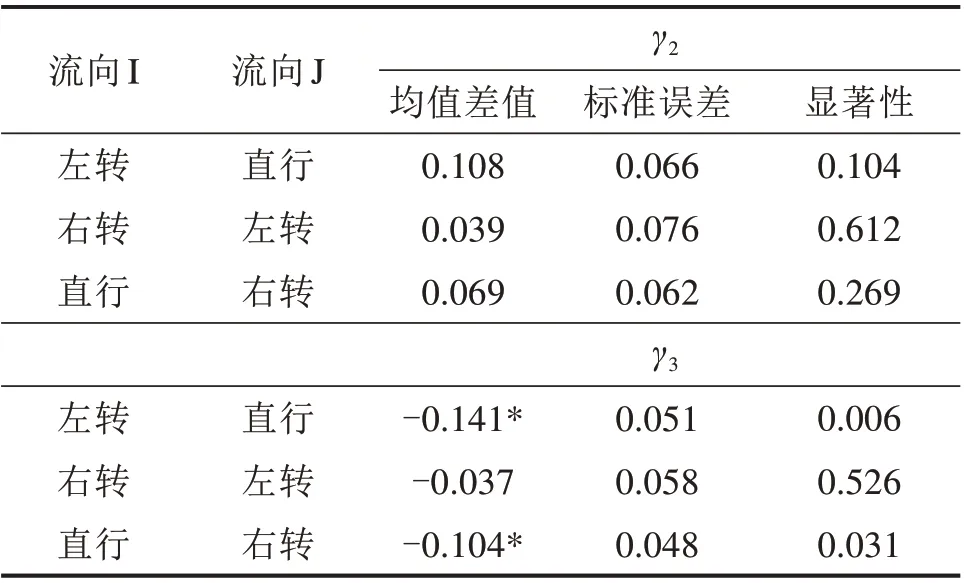
表2 不同转向的参数分析Table 2 Analysis of parameters in different movements
综上分析,驾驶人行为参数在不同交叉口中没有区别,而受转向影响,对于γ3,左右转与直行差异性明显,左右转差异性不大。因此,可以将不同交叉口的驾驶人行为参数合并分析,对于γ3可进一步将其分为左右转、直行2类进行分析。
3 模型整体参数标定
如文献综述所示,模型整体参数标定方法目前主要有边际分布法和多变量分布法。本文在此基础上提出一种基于聚类的多变量分布法,通过比较该方法与边际分布法和多变量分布法的模拟结果,验证该方法对交叉口车流离散度的描述性和适应性。
3.1 边际分布法
边际分布法是对驾驶人行为参数集中的γ2和γ3参数进行统计,得到2个参数的边际分布。与固定值法相比,边际分布法能够体现不同驾驶人的行为特性。
将参数标定得到的400 组数据以γ2,γ3直行参数和γ3左右转参数3 类分别统计,选取4 种常用分布对其进行拟合,并确定最合适的分布。拟合结果如图4 和表3 所示,可以看出,各拟合结果中指数分布的标准误差最小,因此,在边际分布法中,本文采用一元指数分布进行拟合。
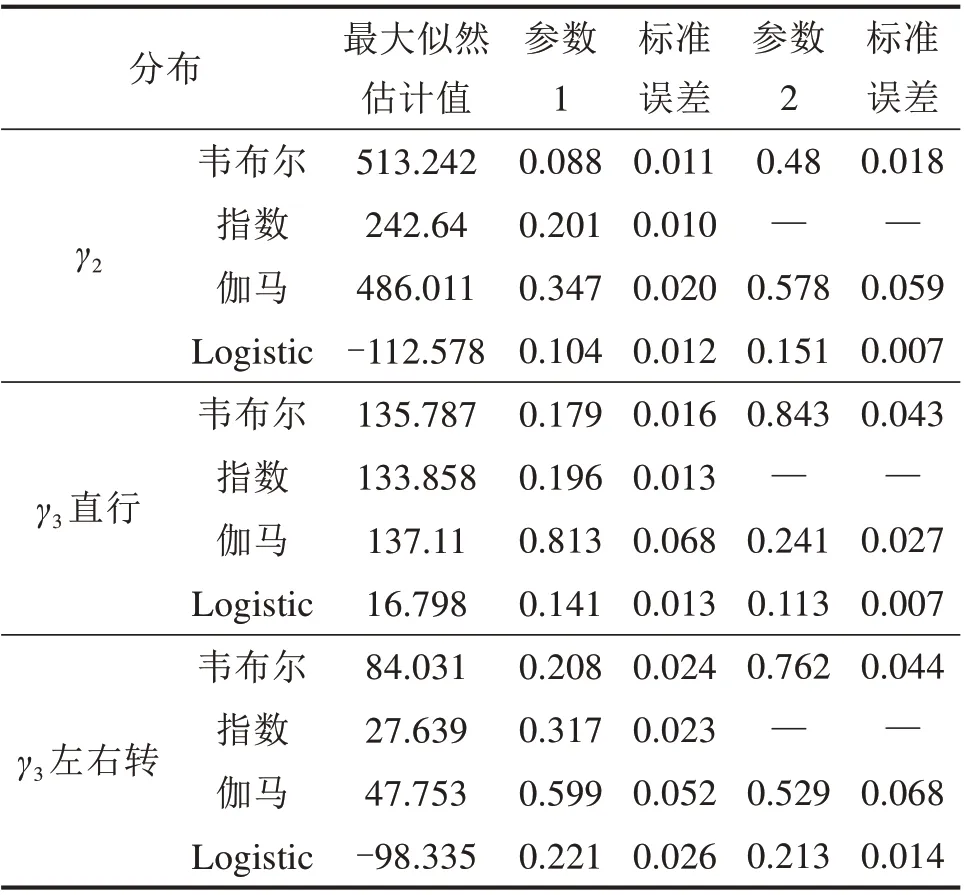
表3 参数拟合情况Table 3 Table of parameter fitting
3.2 多变量分布法
KIM等[12]通过定性分析和仿真分析证实了参数之间是有相关性的,如果单纯用边际分布会忽略这种相关性,产生不可预测的后果,因此,他们提出了一种多变量分布模型,来体现这种参数相关性。
本文首先检验γ2和γ3是否具有相关性。通过Pearson 相关系数(见表4)结果可以看出,二者具有显著的相关性。由于4.2 节采用的是一元指数分布来拟合单个参数,本节采用二元指数分布进行拟合。具体采用BALAKRISHNA 等[22]提出的将2 个分量用乘积和幂形式联系在一起的函数形式,拟合结果如表5所示。

表4 γ2和γ3相关性分析Table 4 Correlation analysis of γ2,γ3

表5 二元指数分布拟合结果Table 5 Fitting results of bivariate exponential distribution
3.3 基于聚类的多变量分布法
本文提出采用聚类方法将驾驶人分类,再通过多变量分布法拟合每一类驾驶人行为参数。相较于将驾驶人归为同一类,根据驾驶人特性将其分为多种类别从逻辑上更为合理。本文采用K-均值算法。
在使用K-均值算法之前,要确定K值。为了找到最合适的K值,分析了K与d之间的关系,如图5 所示,其中d为所有点到该类质心点之间的距离和的平均值。当聚类数等于3时,已能达到较好的划分效果,故将聚类数取3。
K-均值聚类遵循一个迭代过程,以最小化目标函数成本。这种迭代过程容易受到局部最优的影响,也就是说,同样的数据可能会出现不同的聚类结果,因此通过重复10 次算法,选择目标函数成本最小的一次结果作为最终的分类结果,如图6 所示。由于γ3直行与左右转差异性明显,因此需要将直行、左右转分别进行讨论。如表6 所示,对于直行车辆,各点到聚类中心的平均距离为0.079;左右转车辆,各点到聚类中心的平均距离为0.021。
通过上述聚类分析,将驾驶人分为3类。但现实中,每个驾驶人的驾驶行为都是不同的,即使是同一类的驾驶人,其驾驶行为也会有细微的差别,因此需要进一步将每一类参数组合进行多变量分布拟合,以更精准地捕捉驾驶人的行为差异。
由于聚类后,每一类的点都比较集中,而且范围较小,可采用二元均匀分布对每一类进行拟合。设随机向量(Γ2,Γ3),则均匀分布密度函数如式(9)所示。拟合结果如表7所示。
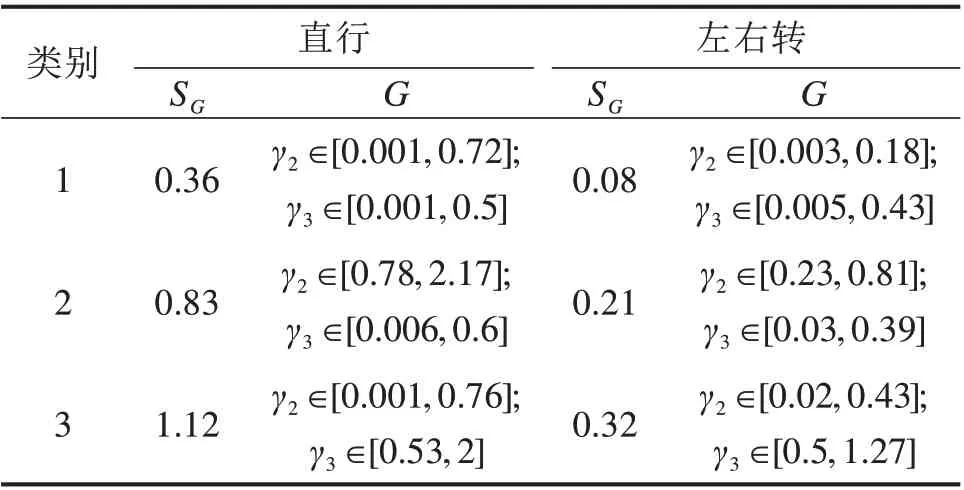
表7 各流向分布情况Table 7 Distribution of each flow direction
式中:G是平面上的有界区域,其面积为SG;c为各类驾驶人出现的概率,即表6中各类占比。
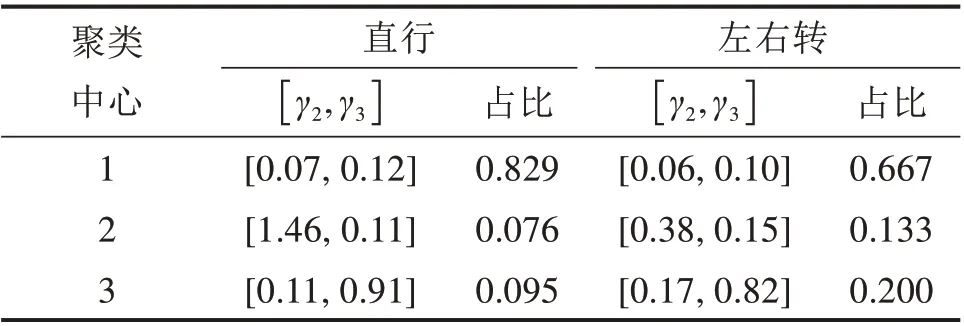
表6 聚类中心结果统计Table 6 Table of straight clustering results
4 模型检验
为检验模型的适应度,先对参与参数标定的4个交叉口的直行和左右转车流进行检验,再选取未参与参数标定的5号交叉口的直行和左右转车流进行检验。
4.1 评价指标
采用1,2,3 和4 号交叉口的数据来检验各种模型参数取值方法对通行轨迹离散型的描述性,采用5号交叉口的数据来检验各种模型参数取值方法对通行轨迹离散型的准确性。以每辆车的起始状态数据和终端状态数据作为轨迹模拟的起始状态与终端状态输入,其他参数输入方法与第3节相同,驾驶人特性参数依据第3 节的3 种方法输入,分别仿真5 号交叉口的直行车流和左右转车流的轨迹。
采用轨迹重合度指标来表征模拟结果与现实的吻合程度。轨迹重合度具体通过以下方法计算。将交叉口内部区域划分为多个单元格,每个单元格大小为0.5 m×0.5 m,计算车辆所占据的单元格并记为1次。计算每个单元格仿真车辆的出现次数与实际车辆的出现次数的差占实际车辆出现次数的比值,再求平均值来计算轨迹重合度。用mij表示第i行第j列单元格中仿真车辆出现的次数,nij表示第i行第j列单元格中实际车辆出现的次数,I为单元格的行数,J为单元格的列数,则单个单元格的重合度Pij可表示为式(10)。
pij的范围为[0, 1],因此,当实际轨迹和仿真轨迹同时出现的单元格中,定义出现次数较少的作为分子,较大的作为分母。则轨迹重合度可由式(11)表示。由定义可知,轨迹重合度越大,说明仿真结果越好。
4.2 参与标定交叉口仿真验证
对参与参数标定的4个交叉口的模拟轨迹与真实轨迹进行对比,通过计算轨迹重合度来检验仿真结果。从仿真结果可以看出(见表8),聚类均匀分布法与一元指数分布法和二元指数分布法相比,仿真效果最好,轨迹重合度最高。在直行车流仿真中,各方法的仿真结果相差不大且均较好,聚类均匀分布法得到的轨迹重合度最小为0.971,最大为0.982。在左右转车流仿真中,聚类均匀分布法表现出了明显的优势,聚类均匀分布法得到的轨迹重合度最小为0.901,最大为0.949。从直行车流和左右转车流的仿真验证中可以看出,聚类均匀分布法能够较好地描述交叉口车辆轨迹离散情况(见图7)。
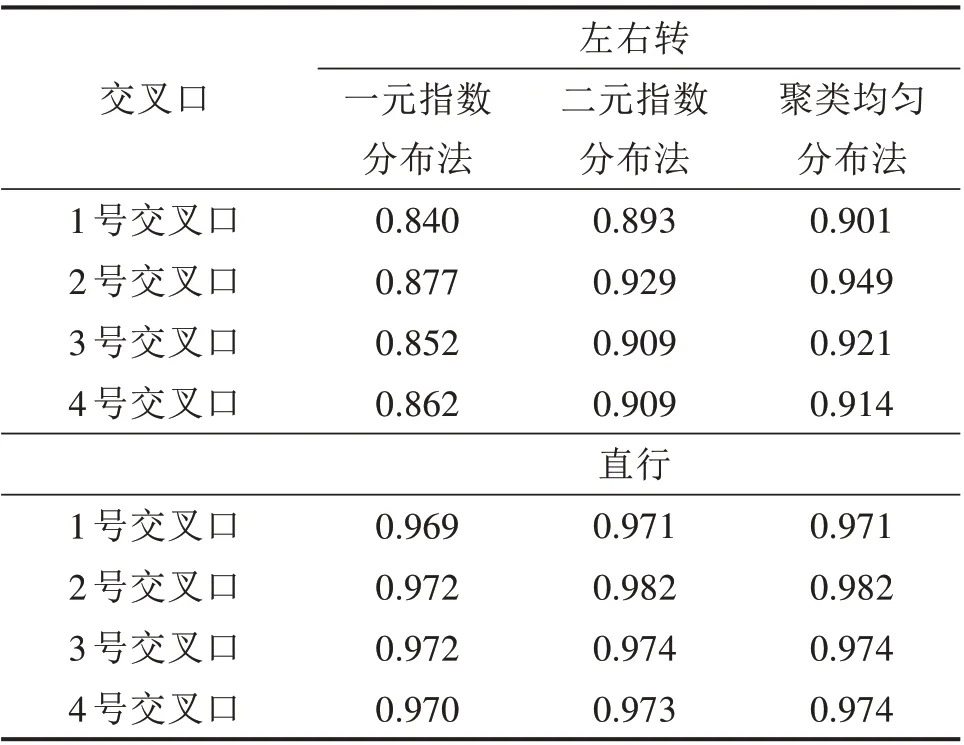
表8 交叉口车流仿真轨迹重合度Table 8 Simulation track coincidence degree of left-right turn traffic flow at intersections
4.3 新交叉口仿真验证
为了验证模型的适应性,进一步对未参与参数标定的5号交叉口的直行和左右转车流进行仿真验证,驾驶人行为参数取值方法与4.1 节一致。从5 号交叉口左右转车流仿真结果可以看出,在一个没有参与标定的交叉口,本文提出的聚类均匀分布法的对于转向车流的仿真轨迹重合度同样最高(见表9),并能较好地体现转向车流的轨迹离散现象(见图8)。虽然较表8 准确度有所下降,但也是可以接受的。这是因为进行拟合的参数集是来自于参与标定的交叉口,因此新交叉口仿真的准确度略小于参与标定的交叉口仿真准确度也是合理的。
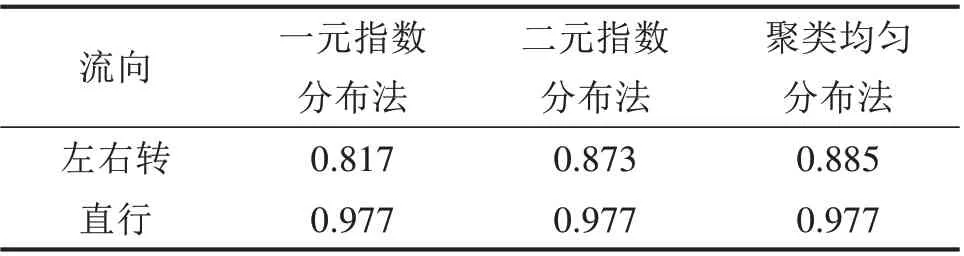
表9 5号交叉口车流仿真轨迹重合度Table 9 Simulation track coincidence degree of traffic flow at intersection 5
从仿真结果可以看出,利用基于聚类的多变量分布法选取驾驶人行为参数,无论是仿真现有交叉口还是新交叉口,仿真结果都是最好的。与传统的边际分布法和多变量分布法相比,基于聚类的多变量分布法能够较好地描述交叉口车流的实际情况,并且具有较强的适应性。
从不同流向来看,与左右转车流相比,直行车流的仿真效果较为稳定。从驾驶行为来看,直行车辆的角度变化不大,主要进行加减速操作,因此,轨迹可覆盖范围较小,驾驶行为决策的可选择性不多。对于左右转车辆,角度变化很大,要同时进行转向操作和加减速操作,因此,轨迹可覆盖范围相对较大,驾驶行为决策的可选择性较多。
5 结论
1) 驾驶人行为参数取值与流向(左转、直行、右转)的相关性明显。
2) 基于聚类的多变量分布法能够很好地描述交叉口车流的实际情况,并且具有较强的适应性。对于参与驾驶行为标定的交叉口,轨迹分布的重合度可达到90%以上;对于未参与驾驶行为标定的新交叉口轨迹分布的重合度也能达到88.5%。
3) 基于聚类的多变量分布法相比以往的交通流参数拟合方法,其优势主要体现在对转向车流通行轨迹离散性的描述。对于直行车流,未见明显差异。
本研究为交叉口交通流仿真中驾驶行为参数选取提供了一个可行的方法,对描述交叉口车辆轨迹离散化提供了一个可行的方案。以本研究为基础,可以进一步探究在冲突交通流中的驾驶行为参数选取方法,并探究不同交叉口规模和不同交叉口角度对模型轨迹离散性的影响。
