关于概率论中近似计算问题的几点标记
2022-10-22李浩
李 浩
宿州学院数学与统计学院,安徽宿州,234000
为了计算随机事件的概率,需要对该事件进行描述,描述方式可分为定性与定量两种。一方面,若采用定性的方式,在缺乏一定的条件下,所求事件的概率精确值不易求得,但从实际应用的角度看,只需得到概率的近似取值范围即可,例如概率论中的加法公式与切比雪夫不等式就可以较好地体现近似计算思想;另一方面,若采用定量描述的方式,等价地刻画所求事件概率,一般需要知道随机变量服从的分布,但是某些分布在具体计算时比较麻烦。例如,服从二项分布的随机变量,当参数n较大时,事件概率的计算量将会非常大,很难得到精确值。若能求出二项分布的近似分布,则可以利用近似分布加以计算,这样会起到事半功倍的效果,而泊松定理正是用于刻画二项分布的一种近似分布;最后,当随机事件需要使用一组随机变量和的形式进行描述时,其概率值更是难以精确计算,若这组随机变量符合某些特性(独立同分布),则可以利用大数定律与中心极限定理,近似地计算“和事件”(一组独立分布的随机变量和)的概率,例如棣莫弗-拉普拉斯定理揭示了正态分布是一组服从二项分布的随机变量和的极限分布,该定理恰是近似计算思想的重要体现。以下我们将从概率论教材中的几个具体方面进行归纳近似计算思想,并加以举例说明并给出标注加以阐述每种近似计算的实际特点。
1 加法公式
对于任意两个随机事件A,B,有
P(A∪B)=P(A)+P(B)-P(AB)
此公式称为概率的加法公式[1]。
由加法公式可知,当事件A与事件B的概率都已知时,如果A与B同时发生(AB)以及A与B至少有一个发生(A∪B),两者中有一个是给定的,则另一个的概率可以求得,否则另一个的概率只能计算取值范围,然后根据实际情况取定一个可能的近似值。
例1在某局部战争中为了执行特殊任务,空军需要出动两款不同型号的战机协同作战。据资料显示,在特殊环境下其中一款战机被击落的概率为0.45,另一款战机被击落的概率为0.57,求两款战机同时被击落的概率。
解:设A为第一款战机被击落,B为第二款战机被击落,则两款战机同时被击落为事件AB。
根据加法公式,可得
P(AB)=P(A)+P(B)-P(A∪B)
由概率具有的规范性可知,0≤P(A∪B)≤1,则
P(AB)≥0.02。
例2已知P(A)=0.82,P(B)=0.75,证明P(AB)≥0.57。
证:根据加法公式,P(AB)=P(A)+P(B)-P(A∪B)
由概率的规范性可知,0≤P(A∪B)≤1,则
P(AB)≥0.82+0.75-1=0.57
得证。
注:(1)在实际生活中,人们更关心两个随机事件同时发生的可能性大小,所以利用加法公式可以粗略地估计其取值范围,再根据实际设定一个经验值;
(2)在例1中由于两战机需要协同作战,故两战机被击落对应的两随机事件之间不具有相互独立性,所以不能利用事件的独立性进行求解;
(3)尽管概率的加法公式形式上较为简单,但是在近似计算随机事件的概率时比较有效。
2 泊松定理
设λ>0是一个常数,n是任意正常数,设npn=λ,则对于任一固定的非负整数k,有
此定理称为泊松定理[2]。
由泊松定理可知,二项分布的极限分布就是泊松分布。当满足定理中的条件时,可以利用泊松分布近似计算二项概率。即若X服从B(n,p),当n较大,并且p较小时,X近似服从P(np),则有
例3假设某保险公司有1 000人投保一款交通旅游人身意外险,投保人在保险约定的时效内发生人身意外的概率约为0.001,且各投保人在保险期是否发生意外是相互独立的。求在保险约定的时效内至少有4人发生人身意外的概率。
解:设X为保险期内发生人身意外的投保人数,由题意可知,X服从B(1 000,0.001),则
=0.019 597
例4设实验室机房有80台同类型电脑,各台工作相互独立,电脑发生故障的概率为0.01,且一台电脑的故障只能由一名技术人员负责处理。现有4名技术人员维护,每人负责20台。计算机房电脑发生故障时不能得到及时维护的概率。
解:设X表示“一名技术人员维护的20台电脑中同时发生故障的台数”,以Ai(i=1,2,3,4)表示事件“第i名技术人员维护的20台中发生故障不能得到及时维护”。设A为事件“机房电脑发生故障时不能得到及时维护”,则所求概率为
P(A)=P(A1∪A2∪A3∪A4)
因为P(Ai)=P(X≥2),i=1,2,3,4。而X服从B(20,0.01),近似地理解为X服从P(0.2),则有
P(Ai)=P(X≥2)=1-P(X<2)
≈0.017 5

(3)在概率论教学过程中,需要重点掌握泊松定理的证明,其证明方法利用到高等数学极限思想,极限思想正是近似计算思想的重要体现。
3 切比雪夫不等式
设随机变量X的数学期望E(X)及方差D(X)都存在,则对任意ε>0,有
成立,此不等式称为切比雪夫不等式[3]。
例5假设某项投资的平均收益为10万元,风险为5万元。求该项投资的收益在7万元至13万元之间的概率。
解:设X为该项投资的收益,由经济学意义可知,其平均收益为E(X),风险为D(X)。
则所求概率为P(7≤X≤13),由于收益X的分布情况未知,故求不出此概率。但利用切比雪夫不等式可求出该概率的近似值。根据切比雪夫不等式,可得
现取ε=3,将其带入式,可得
例6利用切比雪夫不等式粗略理解“3σ”法则。
解:当X服从N(μ,σ2)时,有
P{μ-σ P{μ-2σ P{μ-3σ 这说明尽管随机变量X的取值范围是R,但它的值落在(μ-3σ,μ+3σ)内几乎是肯定的事,这就是所谓的“3σ”法则。 设随机变量X的数学期望E(X)=μ,方差D(X)=σ2,则 (i)取ε=σ,由切比雪夫不等式得: 即0 (ii)取ε=2σ,由切比雪夫不等式得: 即0.75 (iii)取ε=3σ,由切比雪夫不等式得: 注:(1)当随机变量X的具体分布未知时,切比雪夫不等式可粗略地计算概率的近似值;当随机变量X的具体分布已知时,则不必使用切比雪夫不等式,可选取其他更有效的近似方法。 (2)切比雪夫不等式揭示了随机变量的数学期望与方差之间的内在联系,通过两者之间的关系,可以得到随机变量落在以数学期望为中心、方差的倍数为半径的开区间内的近似概率值,尽管近似程度不太精确,但是只有数学期望与方差两个数字特征的情形,切比雪夫不等式不失为一种较为有效的近似计算工具。 此定理称为棣莫弗-拉普拉斯中心极限定理[4]。 例7设有1 000个私家车主投保某保险公司的机动车车险,保费为2 600元,保险期限为1年。该保险规定,被保车辆在保险期间发生,则可获得3万元理赔额。假设车主在1年内发生车险的概率为0.5%,求保险公司此项业务发生亏损的概率。 解:设Xi为第i名私家车主在1年保险期内发生交通意外的人数,则 此外,由题意可知X~B(1 000,0.005),于是保险公司亏损的概率为 P(2 200×1 000<200 000X)=P(X>11) =1-P(X≤11) ≈1-Φ(2.69) =0.003 6 注:(1)由于二项概率在计算时会涉及计算量比较大的问题,因此采用棣莫弗-拉普拉斯中心极限定理加以近似计算会起到较好的效果。 (3)对于独立不同分布的随机变量序列,在满足一定条件下,则可以利用李雅普洛夫定理,可求出随机变量序列的和分布的渐近分布,于是可以利用其渐近分布进行近似计算。 解:当抽取方式为有放回时,由于样本总数不发生变化,所以X的分布律为 当抽取方式为不放回时,由于样本总数发生变化,所以X的分布律为 (2)事实上,对于样本总数不是足够大时,有放回与无放回两种抽取方式对计算某些随机事件的概率结果也没有任何差别,例如抽奖券问题、抓阄问题。于是当样本总数较少时,一般利用无放回方式近似计算有放回方式。 例9在例8的基础上,取m=40,N=100,n=4,计算在抽取的4个球中的有2个黑球的概率。 解:由题意可知X服从超几何分布H(4,100,40)。此外40和100远大于4,所以X可近似服从参数是4,0.4的二项分布。于是 注:(1)在本例中使用超几何分布来求解可得概率精确值,若利用二项分布近似求解可得概率的近似值。当样本总数较大时,采用二项分布近似计算效果较好。 (2)在某种程度上,与可以将二项分布理解为超几何分布的渐近分布,在计算分布概率时可以灵活运用。 P{Sn=n}=P{n-1 解:根据Stirling公式,可得 注:(1)在此例中要计算1010,e-10两个数比较麻烦,但利用Stirling公式加以近似计算会便捷许多。 (2)有关Stirling公式的证明方法较多,相比较代数方法而言利用概率的方法比较易行,通过假设满足一定前提条件,结合标准正态分布进行近似计算。 注:考虑到积分区间为[a,b],本例可以利用服从均匀分布的随机变量的性质证明。 在一些日常生活与理论研究中,经常会涉及计算随机事件的概率问题,在满足一定条件要求下,往往只需得到其近似值即可。例如当随机变量服从一些重要的概率分布时,在具体的计算过程中会涉及一些比较繁琐的计算式,结果不易得到。若运用加法公式、泊松定理、近似分布和中心极限定理等理论工具加以近似计算,可以起到事半功倍的效果。因此近似计算方法与思想在概率论教学中具有很重要的作用。文中详尽地归纳了几种常见分布的近似分布及近似计算问题,相应地标注了在不同的条件下,列举了若干近似分布的计算实例。
4 棣莫弗-拉普拉斯中心极限定理

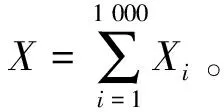

5 利用超几何分布近似二项分布[2]

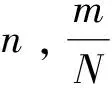
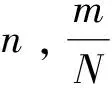
6 利用泊松分布证明Stirling公式[5]





7 利用均匀分布近似计算积分[6]


8 结束语
