人工智能技术气候预测应用简介

杨淑贤,零丰华,应武杉,杨松,罗京佳

南京信息工程大学 气候与应用前沿研究院/气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心,江苏 南京 210044

近年来,热浪、干旱、洪涝、风暴等极端天气气候事件频发,严重影响着当地经济、工农业发展以及人民的生命财产安全。例如,世界气象组织(WMO)发布的《2020年气候服务状态报告》指出，2018年全球约有1.08亿人遭受风暴、洪涝、干旱和野火等灾害影响,到2030年这一数量将增加近50%,每年的损失约为200亿美元。英国公益团体基督教救济会2020年12月28日发布报告称,2020年大西洋出现30个获得命名的飓风,打破了历年纪录,导致至少400人死亡、直接经济损失410亿美元以上。2019—2020年澳大利亚发生规模空前的山火,烧毁20%的森林,烧死成百上千万只野生动物(Komesaroff and Kerridge,2020)。由此可见,气候变化带来的影响已不容小觑,并且气候变化具有很强的敏感性,往往海洋温度变化0.5 ℃就能引发强烈的海气相互作用(Trenberth,1997;Trenberth and Stepaniak,2001),导致全球多地的气候发生异常(Rasmusson and Wallace,1983;Glantz et al,1991;McPhaden et al.,2006),影响人类社会的进步和发展。

为了更好地应对环境以及气候变化,从古至今人类一直在试图理解客观世界和预测未来。预测的方法和手段已经发生了天翻地覆的变化,地球科学领域的预测也从古希腊哲学推理发展到数值模式预报。虽然目前数值天气预报取得了很好的进展,但是气候预测水平并没有很大的提高(Reichstein et al.,2019),准确的短期、长期气候预测以及洪涝干旱等极端事件的预测仍然是主要挑战。目前气候预测主要分为两种方式,一种是基于预测对象和预测因子之间线性关系的传统统计方法,例如多元线性回归(Multiple Linear Regression,MLR)(Cannon and McKendry,2002;Mote,2006;Mekanik et al.,2013)、主成分分析(Principal Component Analysis,PCA)(Ehrendorfer,1987;McCabe and Dettinger,2002;Moradkhani and Meier,2010)、奇异值分解(Singular Value Decomposition,SVD)(Yun et al.,2003;Qiu et al.,2007;Fattorini and Brandini,2020)等。这种统计预报关系大多是不随时间变化的,计算比较简单,依据历史资料建立的模型和当前实际状态可快速预测未来,但这种方法并没有充分利用物理知识,也难以准确抓住预测对象和预测因子之间复杂的非线性关系。另一种是基于物理定律对偏微分方程组加入初始条件和边界条件的动力数值模式预报,动力模式可以模拟现象间的非线性关系和预测每一个事件及其不同的影响,迄今为止世界主要国家研发了大量天气和气候预测系统,包括南京信息工程大学气候预测系统(贺嘉樱等,2020)等。但是纯动力模式预测存在两个主要的缺陷:一是数值模式的研发往往需要耗费大量的资源,模式性能的提高十分不易,且普遍存在各种较明显的系统性模式偏差以及空间分辨率不足等问题,限制了预测技巧;二是数值模式预测技巧的高低还取决于初始场,即资料同化方法的好坏以及集合预报方案的构建,尤其是气候预测往往需要研发较好的耦合资料同化方案以及充分考虑观测资料和各分量模式物理过程的诸多不确定性,使得整个预测系统的构建十分复杂(Luo et al.,2008,2015)。

随着数据信息科学与观测技术和设备的快速发展,人们为了更好地监测、模拟和预测大气和海洋的变化,利用卫星遥感、浮标、雷达、固定观测台站等各类手段收集了大量的地球系统数据,目前数据量远超了几十PB。如此庞大的数据量,已经远远超过了传统统计方法处理数据和理解数据的能力。近年来随着人工智能方法爆发式发展,研究人员发现人工智能方法可以帮助地学研究者更加高效地处理地球系统数据,为地球科学研究开启了一个新的方向,例如Shi et al.(2015,2017)。

人工智能的概念最早于1956年被提出(Crevier,1993),机器学习是一种实现人工智能的方法,早期的算法包括决策树、神经网络、聚类、贝叶斯分类、支持向量机、遗传编程等(Kotsiantis et al.,2006;Dey,2016)。随着计算能力的大大提升,深度学习是目前备受关注的机器学习方法之一,它由多个处理层组成并通过学习输入数据来提取特征(LeCun et al.,2015)。这种方法利用包含多个隐含层的神经网络通过拟合的方式将研究目标与输入数据构建联系,从而解决实际问题。当然,深度学习模型离不开大量的训练数据,随着可分析的数据量不断增长,模型的性能也会逐步提高。地球科学拥有大量可使用的观测和模式模拟数据,这使得人工智能可以应用于大气和海洋预测(Jones,2017)。早在20世纪80年代中期,人工智能技术便应用于气象领域,许多学者一致认为大气科学是一门非常适合应用人工智能的学科(Campbell and Olson,1987;Elio et al.,1987;Schizas et al.,1991;Kuligowski and Barros,1998;Malmgren and Winter,1999;Dueben and Bauer,2018;Rolnick et al.,2019)。近年来人工智能迎来了第3次发展浪潮并在多个领域的大数据分析中取得成功,有关人工智能预测气候的论文数量也越来越多(图1),我国发布了《促进新一代人工智能产业发展三年行动计划(2018—2020)》以抓住历史机遇,促进人工智能产业发展,这也给人工智能技术应用于气候预测提供了政策支持。目前人工智能给拥有众多观测、模拟和再分析资料数据的大气和海洋学科的发展带来了新的机遇和挑战,将在下面的章节中一一讨论利用人工智能预测气候的研究进展。

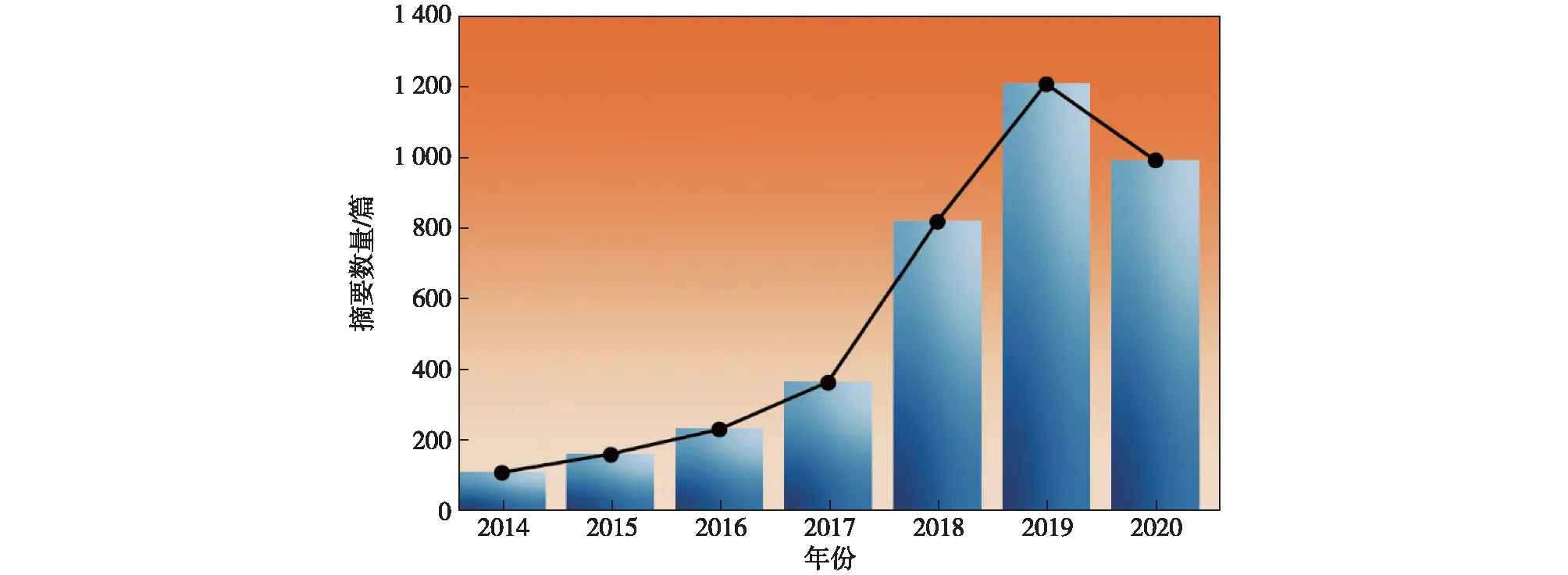
图1 美国地球物理协会上有关机器学习应用的会议摘要数量Fig.1 Number of conference abstracts about machine learning application according to the AGU website

1 人工智能预测气候研究现状

1.1 对资料同化和数值模式进行改进

1.1.1 资料同化

资料同化是一种利用时间演化规律和物理特性的一致性约束,在数值模式的动态运行过程中融合新的观测数据的方法(Bouttier and Courtier,2002)。它是数值模式预测的一个重要步骤,特别是在大气和海洋科学方面,可以为大气和海洋数值预报系统提供准确、合理的初始场。资料同化是一种行之有效的方法,它解决了不均匀的空间和时间数据分布和冗余以便为模式提供大量可用数据集,传统的同化方法包括逐步订正法、最优插值法、卡尔曼滤波和变分方法。然而这些方法不能完全克服它们不切实际的假设,特别是线性、正态性、马尔科夫过程、基础数学模型知识和零误差协方差等(Gilbert et al.,2010)。Geer(2021)提出机器学习和数据同化有很多共同点,都能通过“inverse methods”从数据中了解世界,两者可以在贝叶斯统计方法下统一起来。近年来,许多学者利用人工智能改进数据同化方法,例如Wang et al.(2020)通过构建集成卡尔曼滤波器(Ensemble Kalman Filter,EnKF)和高斯过程(Gaussian Process,GP)误差订正的混合模型来解决不同深度土壤水分数据同化模型的误差,发现EnKF-GP模型可以取得很好的效果,尤其是在输入大量数据和相关的气象数据后。Brajard et al.(2021)提出利用神经网络预测集成卡尔曼滤波后截断模型的误差并将预测的误差加入模型中,这种混合模型预测结果更优于单独的截断模型。Wu et al.(2021)提出多层感知器(Multi-Layer Perceptron,MLP)来学习四维变分(Four-Dimensional Variational,4DVAR)的同化过程,这种快速数据同化方法(Fast Data Assimilation,FDA)的单次分析时间比4DVAR快534倍,证明其可以取代传统的同化方法,解决计算量大、运行时间长的问题(表1)。Arcucci et al.(2021)使用深度神经网络(Deep Neural Networks,DNN)模型来学习资料同化过程,这种深度数据同化(Deep Data Assimilation,DDA)方法使得模型误差在每一次迭代过程中都可以不断减少。此外,Jin et al.(2019)将长短时记忆(Long Short Term Memory,LSTM)神经网络用于沙尘暴预报的资料同化,通过对PM浓度观测资料进行处理,去除PM浓度中的非粉尘部分,使得PM浓度能更好地模拟沙尘暴过程。由此可见,基于机器学习的资料同化方法不仅可以取代传统的资料同化方案并极大地提高计算速度,还可以进一步减少气候预测系统的初始场误差。

表1 FDA和4DVAR的运行(分析)时间的对比(引自Wu et al.,2021)

1.1.2 参数化过程

准确的数值预报系统除了需要数据同化方案提供真实且与模式物理过程协调的初始场之外还需要模拟性能高的数值模式,而数值模式的性能往往受到次网格物理过程参数化的影响。比如,云和对流是地球气候系统最重要最复杂的现象(Krasnopolsky et al.,2013),由于辐射传输过程、水汽凝结蒸发过程等次网格过程在模式中很难直接模拟出来,需要用大尺度变量描述这些次网格过程的统计效应并作为某些物理量的源或汇包含在大尺度运动方程中,即参数化方案。大气和海洋的大尺度环流模式(General Circulation Models,GCMs)是气候模拟和数值天气预报的重要工具。GCMs基于描述解析动力学和热力学(基于能量、动量和质量守恒定律)的方程和表示次网格过程的参数化方案。数值模式预测中这些巨大而长期存在的不确定性根源于参数化方案的不确定性(Schneider et al.,2017)。基于物理模式输出利用机器学习来训练一个统计模型可以很好地表示次网格物理过程,例如基于云解析模型(Cloud-Resolving Model,CRM)的输出结果利用机器学习来训练参数化模型,也称为超参数化(Ukkonen and Mäkelä,2019)。目前CRM已经能减少次网格过程在粗糙网格模式短期模拟中带来的误差,但由于计算资源的限制,往往只能用于短时间的模拟试验。在气候模拟和预测中由于计算资源要求过高,许多学者开始利用深度学习基于短时间云解析模式的结果来训练和构建传统参数化方案的人工智能替代方案,例如Krasnopolsky et al.(2013)使用神经网络集合从CRM模拟的数据中学习随机对流参数化,并在NCAR CAM(National Center of Atmospheric Research Community Atmospheric Model)中进行试验,得到了合理的热带太平洋地区10 a气候模拟。Rasp and Lerch(2018)利用深度神经网络训练出模拟大气中次网格对流过程的替代模型,可以再现CRM模拟的平均气候(图2)。基于Relaxed Arakawa-Schubert (RAS)参数化方案(Moorthi and Suarez,1992)的输出,O’Gorman and Dwyer(2018)评估了利用随机森林(Random Forest,RF)方法训练出的模型在GCM模拟中的性能,这种方法下的GCM运行稳定且准确地捕获如极端降水值等重要的气候统计数据,也能很好地应对全球变暖,并且认为机器学习模型可以用来更好地理解潜在的物理过程。此外,还有一种方法就是通过机器学习构建高分辨率模型或利用高分辨率观测资料来优化GCMs的参数(O’Gorman and Dwyer,2018)。根据Lorenz’96模式的输出进行训练,Gagne et al.(2020)通过输入不同噪声评估生成对抗网络(Generative Adversarial Network,GAN)得到的随机参数化模型,发现GAN可以直接从数据中学习到次网格过程的随机参数化。Yuval and O’Gorman(2020)使用随机森林方法从三维高分辨率大气模式的输出结果中学习次网格过程的参数化。机器学习,尤其是神经网络,可以模拟云和对流中的热量和水汽的垂直输送以及辐射与云和水蒸气的相互作用(Gentine et al,2018)。这些机器学习技术可以与任意数值模式组件相结合,可以更准确地把大气和海洋等数值模式中复杂的次网格物理过程的影响模拟出来,进而取代传统的参数化方案。基于机器学习的参数化方案已被开发用于辐射传输(Chevallier et al.,1998;Belochitski et al.,2011)以及对流和边界层过程(Krasnopolsky et al.,2010;Brenowitz and Bretherton,2018)。目前也在探索将机器学习用于次网格湍流建模(Ling et al.,2016;Wang et al.,2016)。机器学习方法与数值模式融合,可以更有效地改进数值模式的模拟性能以及大幅提高计算效率,进而应用于气候模拟和预测,可以对气候模式的发展和气候预测水平的提高带来深远的影响。

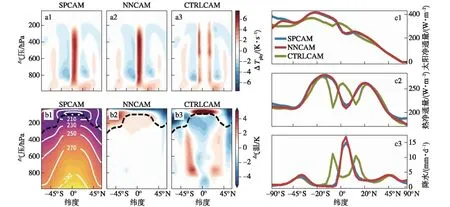
图2 平均对流和辐射次网格加热率ΔTphy(a1—a3;×10-5)、SPCAM的平均温度以及NNCAM和CTRLCAM相对于SPCAM的偏差(b1—b3;黑色虚线表示对流层顶的大致位置,由等值线决定)、大气顶部和降水的平均短波(太阳)和长波(热)净通量(c1—c3)。结果均为5 a经向平均值,并考虑了各纬度的面积加权。其中SPCAM为Superparameterized Community Atmosphere Model v3.0,NNCAM为神经网络次网格模型,CTRLCAM是传统参数化模型(引自Rasp et al.,2018)Fig.2 (a—c) Longitudinal and 5-year temporal averages.(a1—a3) Mean convective and radiative subgrid heating rates ΔTphy;×10-5.(b1—b3) Mean temperature T of SPCAM and biases of NNCAM and CTRLCAM relative to SPCAM.The dashed black line denotes the approximate position of the tropopause,determined by contour.(c1—c3) Mean shortwave (solar) and longwave (thermal) net fluxes at the top of the atmosphere and precipitation.Note that the latitude axis is area weighted (adapted from Rasp et al.,2018)

1.1.3 偏微分方程组求解

既然数值预报模式内的各种组件可以被替换,近年来有学者尝试利用人工智能的方法对数值预报中的动力学、热力学等偏微分方程(Partial Differential Equation,PDE)直接求解,从而通过人工智能方法替换掉数值模式的差分结构。通常偏微分方程求解只能借助计算机采用数值方法求近似解而不可能求得解析解。计算机无法处理连续性问题只能离散化,常见的方法就是有限差分方法和谱方法。有限差分方法简单且边界条件易于处理,但逼近函数的连续性差,模拟的波动移速往往偏慢,在球坐标中极点不好处理以及非线性项的计算容易出现混淆误差等。而谱方法是基于某种正交函数基底离散化方程组,将大气偏微分方程组化为常微分方程组求解,可以给出精确的空间导数的计算,在球坐标系不存在地球极点问题,但不易处理复杂边界问题。人工智能方法在处理离散化以及复杂的边界问题中都有自己独特的方式,例如Long et al.(2018)提出一种新的前馈深度网络(PDE-Net)以准确模拟复杂系统的动力学和揭示隐藏的偏微分方程,与有限差分方法相比,此方法通过卷积神经网络(Convolution Neural Networks,CNN)能有效捕捉物理场边界特征,再构建傅立叶微分算子将整个物理场的变化趋势进行提取,这种微分算子的构建和网络的非线性响应都具有极强的灵活性。而后又提出PDE-Net2.0版本,对PDE-Net版本进行改进,通过卷积来对微分算子数值进行逼近,利用符号多层神经网络恢复模型。相较于PDE-Net,这种方法通过学习微分算子和潜层PDE模型的非线性响应函数,具有最大的灵活性和表达能力,能预测较长时间的动力学过程(Long et al.,2019)。Bar-Sinai et al.(2019)提出了基于已知基本方程的实际解利用神经网络拟合偏微分方程近似解的方法,此方法更加精确,能够求解低分辨率网格上的方程。此外,也有学者通过机器学习算法的改进,使得原本的算法不受限于特定的边界和初始条件进行模拟。Raissi et al.(2020)提出了一种“隐藏的流体力学”网络框架(Hidden Fluid Mechanics,HFM),将六个由原始流体物理方程推导而来的公式加入网络框架中。这个全新的框架既有人工智能的高效性、非线性,又有流体力学的物理约束,该框架对流体物理数据的模拟不仅超越了纯粹使用机器学习进行数据学习的效果、更是超过了传统的使用离散方法求解纳维-斯托克斯方程(Navier-Stokes equations,N-S equations)的方法(图3)。

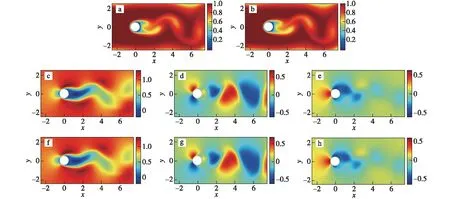
图3 通过圆柱体矩形训练区域的二维流动:(a)输入的浓度;(b)人工智能模型回归出的浓度。根据纳维-斯托克斯方程由图(b)回归出来的速度场u(c)、v(d)和压力场p(e)以及用来对照的同一时刻速度场u(f)、v(g)和压力场p(h)。其中横纵坐标表示二维流动的方向,数值分别表示沿着x,y方向的位移。引自Raissi et al.(2020)Fig.3 2D flow past a circular cylinder with rectangular training domain:(a) A representative snapshot of the input data on the concentration of the passive scalar.(b) The same concentration field regressed by the algorithm.The algorithm is capable of accurately regressing the velocity u (c),v (d),and the pressure p (e) fields (according to Navier-Stokes (NS) equations).The reference velocity (f—g) and pressure (h) fields at the same point in time are plotted for comparison.Finally,the horizontal and vertical coordinates represent the directions of the two-dimensional flow (adapted from Raissi et al.,2020)

1.2 利用观测和模式结果进行智能预测

数值天气预报系统通过改进模式和同化观测数据,技能已经改进许多(Magnusson and Källén,2013),也由于计算能力的提高,实现了更高的模式分辨率和更全面的数据同化(Bauer et al.,2015)。但在摩尔定律消亡的情况下,这一进展不太可能长期继续下去。在这种情况下,模式后处理变得更加重要,有助于在越来越有限的计算资源下推动技能提高。人工智能是开发更强大模式后处理方法的主要候选者,将人工智能/机器学习应用于大气科学问题的最成熟方面可能就是模式输出的后处理(Haupt et al.,2021)。

1.2.1 人工智能预测模型

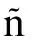
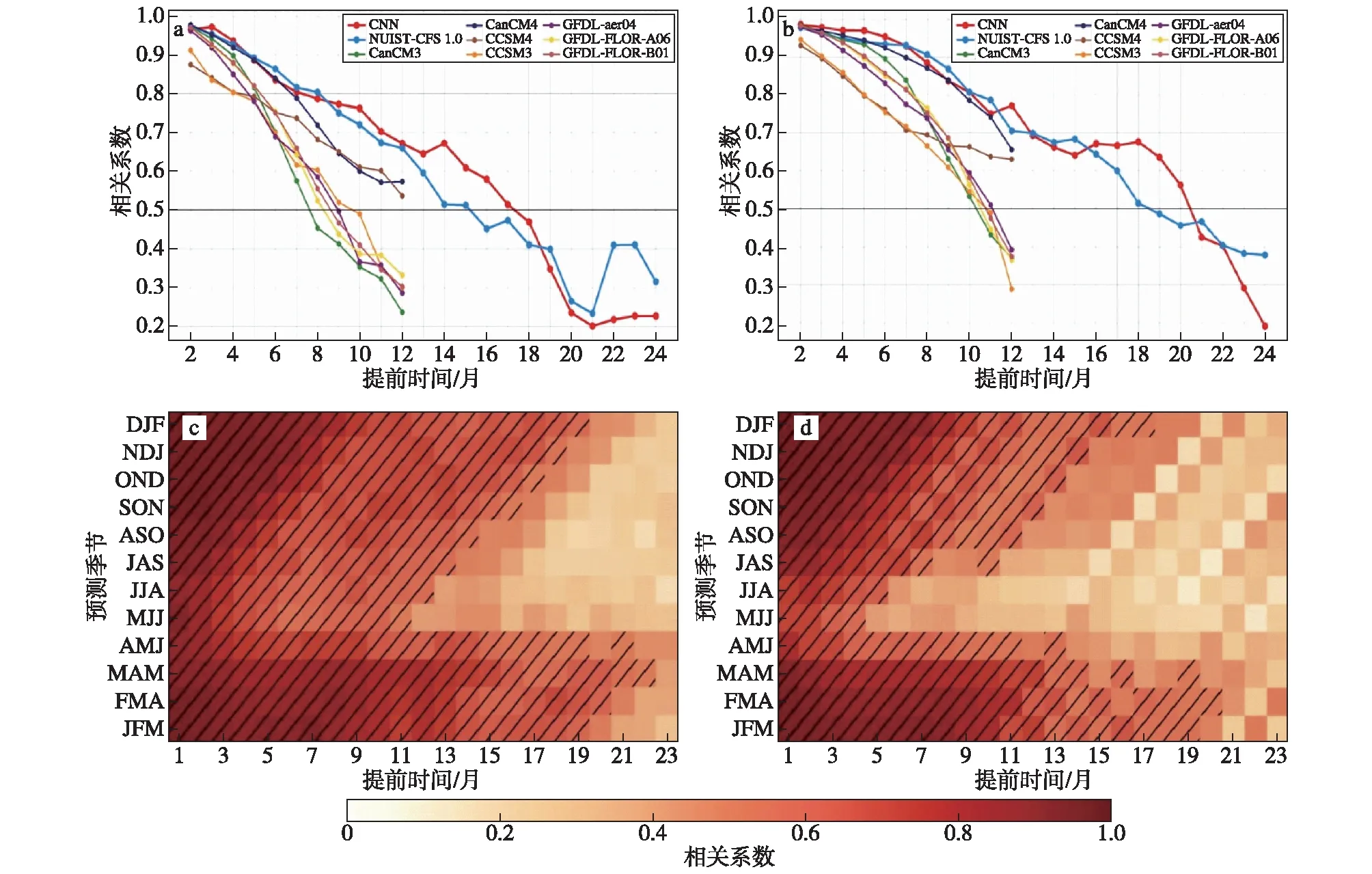
图4 1982—2019年秋季(a)和冬季(b)Nio3.4海温指数的相关系数预测技巧随预测时效(提前1—24个月)的分布(红色为CNN模型、蓝色为南京信息工程大学气候预测系统(NUIST-CFS1.0)以及其他颜色为来自北美多模式(NMME)的动力模式预测系统的结果)。CNN模型(c)和NUIST-CFS1.0(d)对逐季(3个月平均)Nio3.4海温指数的相关系数预测技巧,加斜线部分表示相关系数技巧超过0.5。(c)和(d)引自Ham et al.(2019)Fig.4 The correlation skill of Nio3.4 SST index in boreal autumn (a) and winter (b) as a function of the forecast lead month in the CNN model (red),NUIST-CFS1.0 (blue),and the dynamical forecast systems included in the North American Multi-Model Ensemble (NMME) project (the other colors).The validation (i.e.,hindcast) period is 1982—2019.The correlation skill of the Nio3.4 index in each target season based on the CNN model (c) and NUIST-CFS1.0 (d).The hatching highlights the forecasts with correlation skill exceeding 0.5.(c) and (d) are adapted from Ham et al.(2019)

1.2.2 数值模式产品释用

1)误差订正

数值模式是利用方程组和约束条件来模拟气候系统,由于未能充分代表各类尺度物理过程和离散化算法缺陷等各种因素导致的偏差常常使得气候模拟和预测的性能偏低。模式误差是当前数值天气预报和气候预测提高准确性和可靠性的主要障碍之一。模式预测误差来自初始场误差、模式误差以及外部强迫场误差等(Hawkins and Sutton,2009,2011;Deser et al.,2012a,2012b;Sriver et al.,2015;Yao et al.,2016),主要分为系统性误差和时变误差。系统性误差又称为气候漂移,是由于模式存在偏差,从初始真实场开始经过长期积分会趋向于模式内在的统计平衡状态(即模式气候态),而模式气候态与实际气候态之间存在偏差。而时变误差是模式误差中依赖于时间变化的部分,随环流型而变化(Johansson and Baer,1986;Miyakoda et al.,1986)。近年来许多学者利用人工智能方法订正数值模式误差进行了尝试,例如Moghim and Bras(2017)使用ANN模型对CCSM3(Community Climate System Model version 3)的南美洲北部降水进行订正,通过输入同期和前1、2、3个月降水量以及周围邻近区域的降水平均和标准差,发现ANN模型对所有季节降水的均方差(Mean Square Error,MSE)、偏差(bias)、相关性(ρ)的平均改进率(Improvement,Imp)分别为70.75%、55%和56.5%,相比于线性回归模型63.25%、46.5%和40.75%的改进率,ANN模型显著优于线性回归模型,说明人工神经网络灵活而强大的能力能够有效地用于降水的偏差订正。Lee and Ahn(2018)利用自组织映射(Self-Organizing Mapping,SOM)方法找出隐藏在模式动态预测中有意义的信号来修正预测,发现经过此方法订正后各季节、各预测时效的均方根误差均有所降低,且提前时间越长的预测订正效果越好。Wang et al.(2018)比较了随机森林(RF)、支持向量机(SVM)、贝叶斯模型(Bayesian model averaging,BMA)和算术总平均值(arithmetic Ensemble Mean,EM)四种不同的方法对不同的GCMs进行多模式集合模拟月降雨量和温度方面的能力,RF和SVM在性能标准上比EM和BMA有更显著的改进。Kim et al.(2021)利用LSTM模型对多模式预测MJO(Madden-Julian Oscillation)的结果进行偏差订正,MJO预测的幅度和相位的误差分别显著减少了90%和77%(图5)。诸多研究表明,人工智能模型可以用来对订正动力模式的偏差,从而提高气候预测水平。

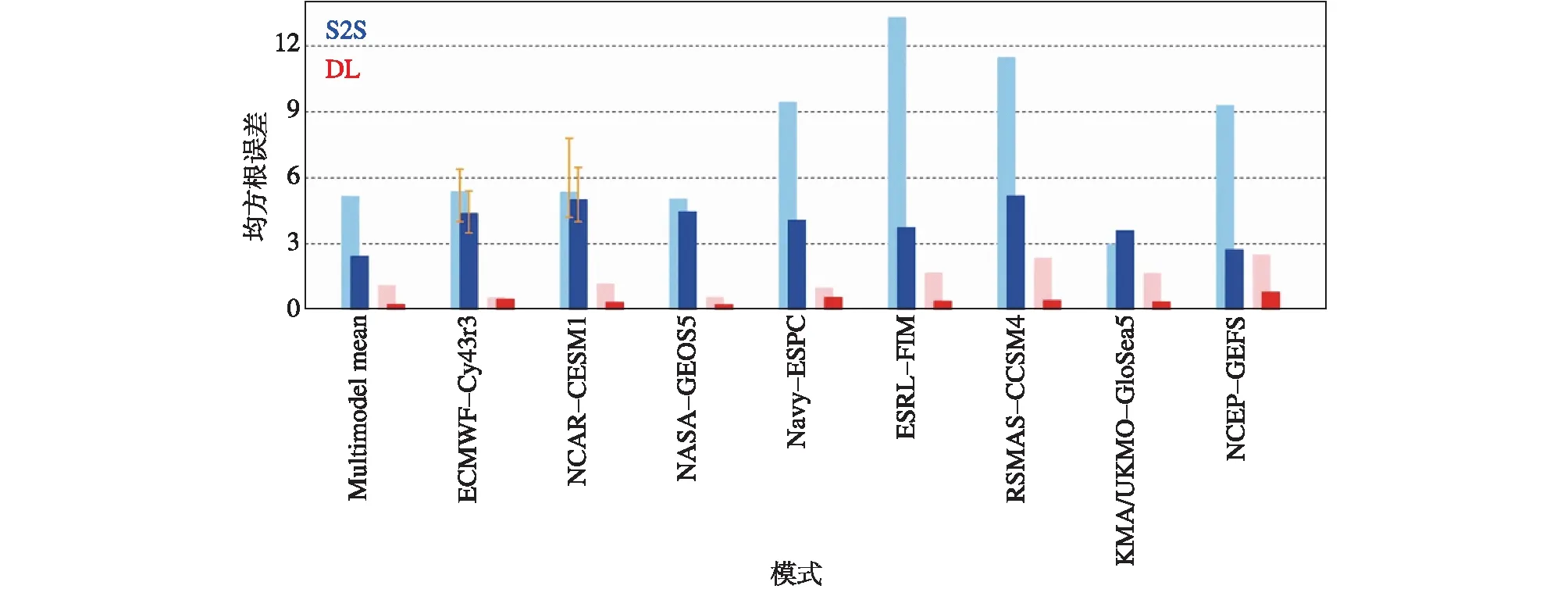
图5 单个模式平均的均方根误差(BMSE,Bivariate root-mean-squared error)。次季节至季节(S2S)预测(蓝色)和深度学习(DL)订正(红色)的均方根误差,其中振幅误差(BMSEa)(深色)和相位误差(BMSEp)(浅色)取4周8个相位的平均。纵坐标表示均方根误差,横坐标的第二到第九项表示用来订正的动力模式,八个模式的集合平均为第一项。引自Kim et al.(2021)Fig.5 Averaged forecast errors in individual models.Bivariate root-mean-squared amplitude error (BMSEa) (darker colors) and phase error (BMSEp) (lighter colors) for subseasonal-to-seasonal (S2S) reforecasts (blue) and deep learning (DL) corrections (red) averaged over four weeks and eight phases.For ECMWF-Cy43r3 and NCAR-CESM1,the orange error bar denotes the 95% confidence interval based on the bootstrap method.ECMWF-Cy43r3,NCAR-CESM1,NASA-GEOS5,Navy-ESPC,ESRL-FIM,RSMAS-CCSM4,KMA/UKMO-GloSea5,and NCEP-GEFS denote the dynamical model for use (adapted from Kim et al.,2021)

2)降尺度

除了订正上述动力模式的偏差之外,由于用来预测气候的GCMs的空间分辨率普遍较低,适合模拟和预测大尺度环流和信息,但在模拟和预测区域气候时,因为空间分辨率低、难以准确刻画气温、降水的小尺度局地变化特征,我们就需要将大尺度、低分辨率的全球气候模式输出信息转化为小尺度、高分辨率的区域气候信息,这种过程称为降尺度。降尺度方法可以分为三大类:动力降尺度方法(Benestad et al.,2008)、统计降尺度方法(Chu et al.,2010)以及统计与动力相结合的降尺度法。动力降尺度有两个发展方向,一种是提高GCM的水平分辨率,例如近20 a来国际上大力发展的下一代全球准均匀高分辨格点模式(McGregor,1996;Mcgregor and Dix,2001;Dudhia and Bresch,2002;Satoh et al.,2008;Ringler et al.,2013),但这需要极大的计算资源支撑。另一种是在GCM中针对有限目标区域嵌套高分辨率区域模式(如WRF等),与第一种方法比可以相对减少计算量,但是存在大尺度模式和区域模式之间边界信息交换不易处理等问题。现有的区域动力降尺度方法的计算量仍较大,计算资源往往难以得到满足。统计降尺度方法则是建立GCM中模拟效果较好的大尺度变量和实测小尺度(或台站)变量之间的统计关系,由于统计降尺度方法的计算量小、性能较高,因此得到了广泛的应用(Beecham et al.,2014;Sachindra et al.,2014,2016;Gutiérrez et al.,2019)。统计与动力相结合的降尺度法结合了物理知识约束和计算效率快的优点,在实际业务中应用更广(Chen et al.,2012;Wang et al.,2015;Ba et al.,2018)。除此之外,近年来人工智能方法也在降尺度领域大显身手。例如,Tripathi et al.(2006)引入支持向量机(Support Vector Machine,SVM)方法对GCM模拟的降水进行降尺度,比流行的基于多层反向传播神经网络方法更有效。Srivastava et al.(2013)通过对比三种人工智能方法(ANN,SVM,RVM)和广义线性模型(Generalized Linear Model,GLM)对提高土壤水分和海洋盐度(SMOS)空间分辨率的能力,发现ANN算法具有更好的性能。Sachindra et al.(2018)提出可以用支持向量机(SVM)或遗传算法(Genetic Programming,GP)方法来建立降尺度模型进行洪水预测或极端降水预测,在研究干旱时使用相关向量机(RVM)降尺度模型等。除了以上的常规方法外,计算机视觉领域中的图像超分辨率(Super-resolution,SR)与统计降尺度非常相似,它通过获取低分辨率(low-resolution,LR)图像并生成近似真实高分辨率(high-resolution,HR)的增强图像(Yang et al.,2014)。随着机器学习特别是基于卷积神经网络深度学习方法的快速发展,它在降尺度上的应用取得了迅速的发展和巨大的成功。Vandal et al.(2017)首次将降尺度过程与图像超分辨率类比,将多个超分辨率卷积神经网络(Super-Resolution Convolutional Neural Networks,SRCNN)叠加在一起建立了深度统计降尺度模型(DeepSD),并加入高分辨率的静态地形数据训练模型,将降水资料的分辨率提高了8倍(图6)。相比而言,DeepSD的效果以及效率远好于其他降尺度方法。但由于过于简化问题以及模型缺乏灵活性,Liu et al.(2020)提出一种具有跳跃连接和融合功能的Ynet模型,可以直接对多个GCM进行降尺度,且性能显著高于DeepSD。另外,Stengel et al.(2020)开发了一种对抗性深度学习方法,并表明该方法能将气候数据分辨率提高50倍。

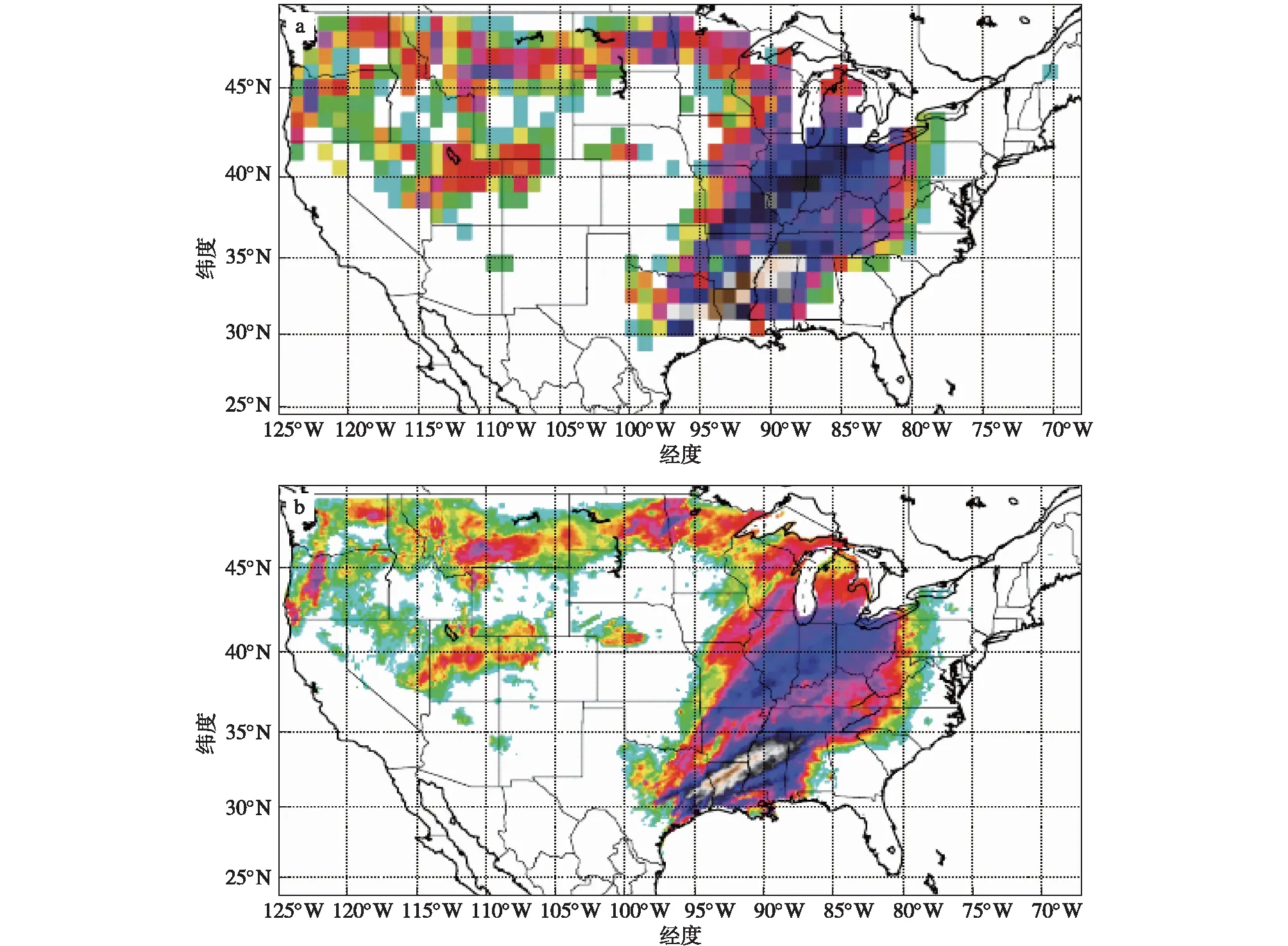
图6 降水分布:低分辨率1.0°(a,约100 km)和通过DeepSD降尺度后高分辨率1/8°(b,约12.5 km)的结果(引自Vandal et al.,2017)Fig.6 PRISM observed precipitation based on (a) low resolution at 1.0° (100 km),and (b) high resolution at 1/8° (12.5 km).Adapted from Vandal et al.(2017)

2 人工智能预测气候面临的关键科学和技术问题

ANN被称为通用逼近器,可以逼近任何非线性确定性函数,即逼近几乎任何连续的输入和输出映射,这一特性被称为通用逼近定理(Hornik et al.,1989;Hornik,1991;Schmidhuber,2015)。气候系统的高度非线性和复杂性,以及它存在的大数据集和有限的训练数据使得气候成为一个有趣的机器学习挑战的领域(Watson-Parris,2021)。表2表示与地球科学任务有关的传统方法与深度学习方法。目前人工智能方法预测气候领域依旧存在许多挑战(Reichstein et al.,2019),列举如下。

1)数据集构建的问题:

随着人工智能方法应用于气候研究领域的兴起,越来越多的实用案例在气候问题的解决上大放异彩,不少学者也认为气候问题仅仅是一个数据问题,认为只要有足够多的数据就可以解决大多数的气候问题。然而,数据的获取以及可利用性等均是不可忽视的问题。

大气和海洋数据来源广泛,根据不同的传感器获得的数据往往具有自身的观测误差,并且在气候对象的预测中仅使用观测资料是不够的。表3突出显示每个数据源的主要优势和劣势。有关气候数据来源的更详细讨论,请参见Faghmous and Kumar(2014a)。当尝试利用模式输出结果作为训练数据来弥补观测有效样本不足时,不同的模式有着各自的系统性误差,增大了数据集中的噪声,如果不基于物理规律进行数据处理,这些误差的存在将会极大程度影响人工智能模型的准确性。此外,对于不同目标的人工智能模型需要构建相对应的数据集,人工智能模型并不像传统动力模式一样,将大量的数据输入到动力模式之后用物理方程约束从而模拟大气和海洋等圈层中的物理过程,过于冗余的数据反而不能对人工智能模型起到积极作用。因此,基于物理规律的因子筛选在建模前也是格外重要的。

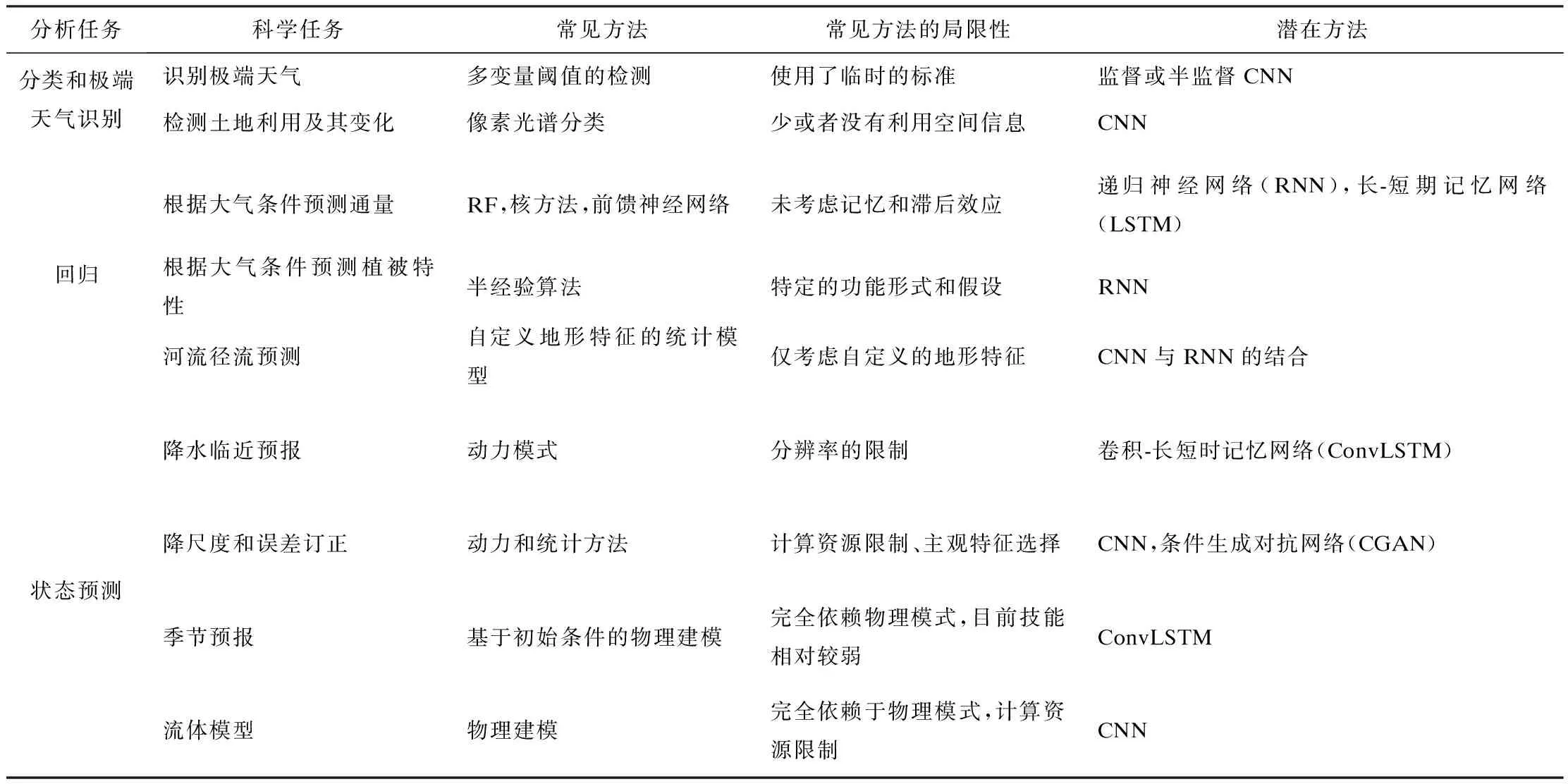
表2 地球科学任务的传统方法和深度学习方法(引自Reichstein et al.,2019)

表3 气候数据来源(引自Faghmous and Kumar,2014a)

除此之外在充分利用气候数据潜力来促进科学发现还存在着许多挑战,例如我们在气候科学中所感兴趣的对象通常是连续时空场中随时间和空间演变的部分,以及许多涉及物理变量之间的复杂关系难以从有限的高质量气候数据中提取等等。全球范围内高质量传感器测量的气候变量数据仅存在于过去40～100 a,这就限制了一些最先进的数据科学算法(如深度学习)的实用性,这些算法在语音和图像识别问题上的成功在很大程度上得益于这些领域大规模的数据可用性(Karpatne and Kumar,2017)。

对于气候预测问题,目前常见的人工智能方法往往是采用监督学习的方式,这就涉及数据集中有效样本集的构建。但是由于很多极端气候事件如干旱、洪涝等并不是每年都会发生,再者动力模式对这种极端事件也没有很好的模拟效果,所以有效样本量相对较小,尤其是年际与年代际预测对象因为观测序列较短,均属于小样本问题。目前针对小样本问题的解决方案有数据增强(Data augmentation)(翻转、剪切、平移等)、迁移学习(Transfer learning)、生成对抗(Generative Adversarial Networks)、元学习(Meta-learning)和零样本学习(Zero-shot learning)等方法(Barto and Sutton,1997;Sung et al.,2018;Taylor and Nitschke,2018;Zhang et al.,2018;Liu et al.,2019;Xian et al.,2019;Zhong et al.,2020;Zhu et al.,2020;Wang et al.,2021),但已有的数据增强方法仅仅适用于图像识别问题,在气候问题上如果将数据进行翻转,其本身的物理意义将完全改变,使模型结果失去物理意义。目前来说利用迁移学习或者将有监督问题转化成无监督问题或许是解决这类小样本问题较好的途径,例如Sap and Awan(2005),Zscheischler et al.(2012),Chalupka et al.(2016),Sathiaraj et al.(2019),Ham et al.(2019)。然而如何使迁移学习等方法能更符合物理规律地应用于解决气候问题,还需要更多的探索。

2)模型的可适用性问题

尽管最近一系列人工智能方法在气候预测中取得了不错的成果,且有越来越多的深度学习/机器学习模型可供选择,这些模型可以在短期或长期气候预测中胜过现有的动力模式预测系统和传统的统计模型,但我们仍不能过于乐观,对于使用类似“黑匣子”一样的深度学习工具进行预测要持怀疑态度。目前很多研究将机器学习与传统的物理知识建模隔离开,这极大限制了这两种方法的融合发展。如果不能在地球科学的机理认识背景下正确应用人工智能技术,人工智能模型结果可能与基本物理知识相背离。

物理过程模式与人工智能预测模型不是相互替代关系,而是互为补充。两者的结合可以有很多方面,主要分为两种:其一是以动力模式为主,比如利用人工智能模型来优化动力模式中的部分参数,或利用人工智能方法替换掉模式中半经验化的参数化方案,或者利用人工智能方法对动力模式结果进行订正和降尺度等;另一种则刚好相反是以人工智能模型为主,将物理过程如动力方程组等加入人工智能模型中,对人工智能模型的构建进行合理的物理约束,或者对动力方程组利用人工智能方法直接建模求解。

最终,构建的动力-人工智能混合模式或模型,应当遵循地学的物理规律,对于理论支持薄弱的部分采取数据驱动为主的策略。越来越多的研究采用在机器学习算法中使用物理定律和守恒性质方面的物理学知识来约束训练并进一步改进算法。例如,基于GAN的湍流模拟模型可以通过在损失函数中加入物理约束,如能量谱(Wu et al.,2020)。基于CNN的次网格尺度物理过程参数化模型可以通过约束全球守恒性质来进一步改进平均气候特征的模拟,例如动量守恒(Bolton and Zanna,2019)。只有致力于将物理模式与数据驱动的机器学习工具两者多功能相结合的混合建模方法,才能在模拟和预测中取得最佳效果,促进两个学科融合,赋予全新的活力。

3)物理解释性问题

人工智能模型一直以来都有一个弱点,就是物理解释性差的问题。高性能的复杂算法和模型大量存在,但它们却缺乏决策逻辑的透明度和结果的可解释性,导致在预测应用中很多学者将人工智能模型认为是一个黑箱模型,无法完全信任。气候科学强调在理解机理的基础上进行预测。人们对预测单个事件很感兴趣,但更多的注意力仍然放在整个系统的规律而不是单个事件上,所以更强调模型的可解释性而不是模型的灵活性(Faghmous and Kumar,2014b)。只有物理上提供一定可解释性的模型才是可取的,因为它可能有助于揭示观测数据中的因果关联,根据数据中反映的内在关系以计算机方法的视角挖掘出物理上全新的联系,从而推动物理规律认识的发展。Toms et al.(2020)为地球科学开发了可解释的神经网络,通过后向优化(backward optimization)和分层相关性传播(Layerwise Relevance Propagation,LRP)这两种方法来有助于确定哪些输入对神经网络的决策过程最有帮助,并展示了它们在提高理解MJO的有用性和可靠性(Toms et al.,2021)。McGovern et al.(2019)介绍了如何应用机器学习方法来更好地理解物理学,且这些方法已证明对确定性预测的改进是成功的(Bremnes,2020;Rasp and Lerch,2018)

常见的探究物理解释的方法可以根据建模过程分为三类,分别是输入数据(或预测因子)选取的可解释性、建模中模型基于物理机理构建、以及模型输出结果的可解释(Reichstein et al.,2019;Murdoch et al.,2019;Barredo,2020;Camps-Valls et al.,2020;Kashinath et al.,2021)。目前在气候预测中被广泛关注的是结果的可解释性,可解释性越高则模型结果更为可信。主要用到的方法为隐藏层分析,即通过提取隐藏层中的权重,可视化分析模型关注区域,并根据可解释结果结合理论认识来解释物理机理。此外还可以采用敏感性分析等方法,将模型输入变量在可能的范围内变动,研究和评估这些属性(或预测因子)的变化对模型输出结果的影响程度。我们将影响程度的大小称为该属性的敏感性系数,敏感性系数越大就说明属性对模型输出的影响越大。

当然这些方法要合理的应用到气候预测领域还有很多问题亟待解决,比如有的预测模型虽然具有很好的预测效果,但是模型的可解释分析或许与现有物理规律的认识明显背离,或者数据信号中噪音过多、可解释分析并不显著等。如果能够解决这些问题,建立具有可解释性的人工智能模型,根据可解释结果或许可以有效地推动气候预测的理论和方法发展(图7)。

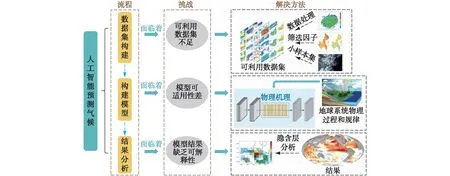
图7 人工智能预测气候的流程图、面临的挑战及其可能的解决方法Fig.7 Flow diagram of climate prediction by means of artificial intelligence,the challenges it faces and potential solutions

3 结论与讨论

随着观测手段和方法的快速发展,地球科学研究面临的数据量将越来越多,也面临着国家和社会发展越来越高的需求,更为准确的天气/气候预测结果能更好地为防灾减灾服务。由于计算资源的限制,高分辨率的数值模式预报系统已略显疲态,而人工智能方法特别是深度学习通过大量数据驱动建立基于物理解释的预测模型有希望成为动力模式的一种有力补充工具。两者相辅相成,共同促进发展,可以更好地改善大气和海洋预测,图8展示了地球系统模式与人工智能相融合的阶段。对于人工智能模型的发展,有三个主要建议,如下。

1)根据不同的预测任务结合气候机理构建数据集

气象数据具有多源、多尺度、多维、非线性、滞后性等特性。人工智能方法要想更好地应对预测问题,必须要结合气候预测机理,充分考虑数据之间的因果关系、时空关系。对于小样本的数据问题,合理恰当地使用人工智能方法进行数据增强或迁移学习。

2)模型构建的合理性与可解释性

构建的人工智能模型不仅结果要准确,而且要可信,包括在构建模型的过程,要充分考虑模型构建的物理合理性,不能把时空预测问题简单地转化为空间上的相互关系或者时间上的连续性。如果能利用数值模式中的动力学方程对人工智能模型进行约束使智能模型本身具有物理约束,将极大地增加智能模型的物理可解释性。而对于智能模型给出的预测结果,要尽可能对模型结果进行可解释性分析,解释模型通过哪些特征做出的预测,使得模型变得更加透明,将黑盒子变成灰盒子。

3)更多尝试与动力模式结合

动力模式和人工智能模型并不是两个独立个体,也不是相互替代的关系,两者只有相互融合才会产生最好的效果。动力模式中仍有很多不全面的地方,比如空间分辨率不高、极其消耗计算资源的复杂参数化过程、资料同化过程以及一些复杂过程的半经验半理论的拟合。如果将两者相互结合,或将真正实现数字地球,更好地模拟天气/气候变化。

总的来说,未来的智能模型应该既包含物理过程约束又应用大数据人工智能的方法。数据驱动的人工智能方法不会取代物理模式,而是会对其进行有力的补充和丰富。具体来说,这些智能模型应该遵守物理定律,使用可解释的结构框架并且在理论薄弱的地方遵循数据驱动。这两个交叉学科的合理碰撞与融合一定会激发全新的活力推动各自的发展,为应对未来气候变化和提高气候预测水平提供强有力的科技支撑。

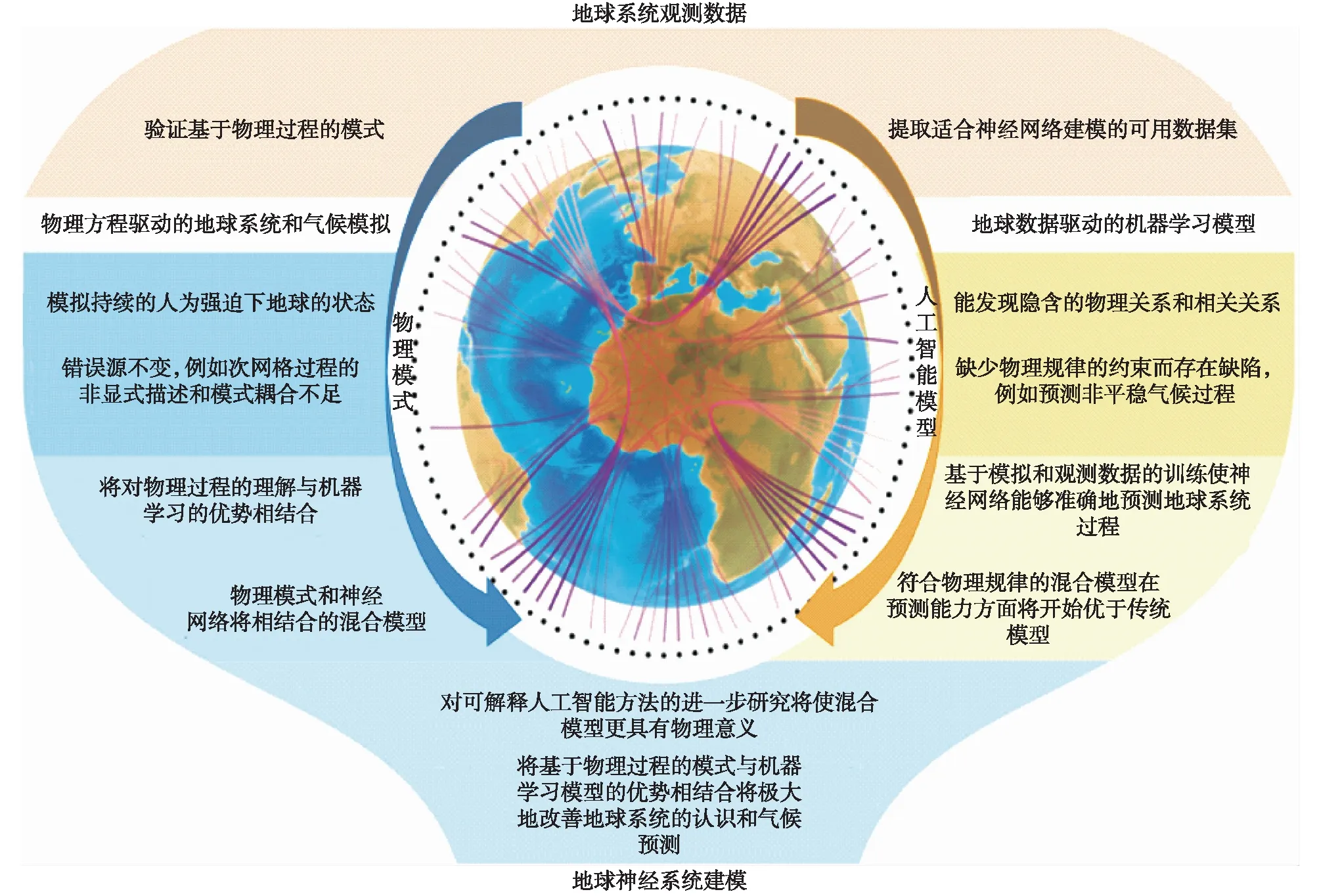
图8 地球系统模式与人工智能相融合的不同阶段(改编自Irrgang et al.,2021)Fig.8 Successive stages of the fusion process of Earth system models and artificial intelligence (adapted from Irrgang et al.,2021)