复杂受力轴上轴承正装与反装选择探究
2022-10-21段泓毅
段泓毅
(成都理工大学 机电工程学院,四川 成都 610059)
0 引言
在大部分机械类参考用书中[1-4],对于圆锥滚子轴承的正装与反装,一般只提到了其各自在结构上的特点以及对应的单一受力情况,而对于复杂受力情况下轴承安装形式选择未有系统的分析。
对于角接触球轴承和圆锥滚子轴承来说,其拥有“正装”和“反装”两种安装形式[5],如图1所示。
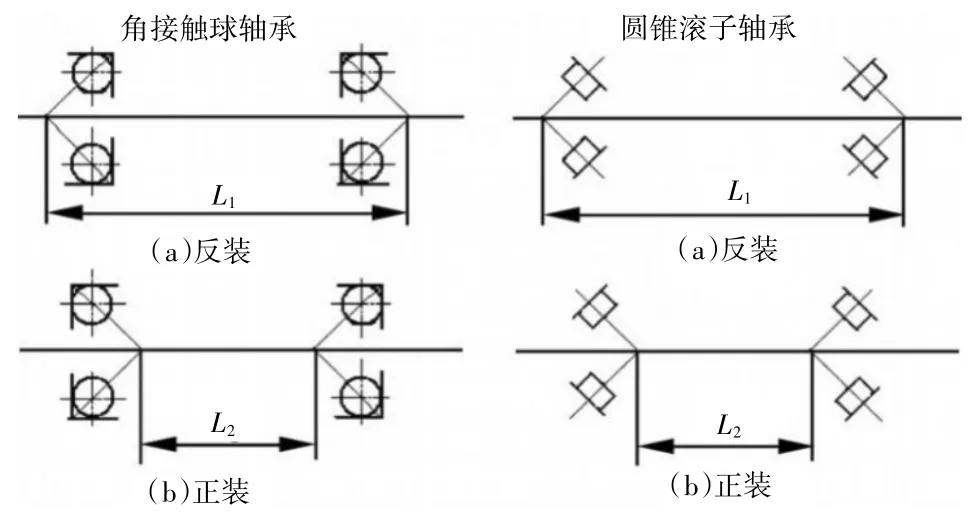
图1 正装反装示意图
由图1可看出,正装可以使轴承对轴的支撑跨距相对几何中心距减小,从而减小处于两轴承中间载荷对轴造成的挠度(扭曲变形);而反装恰恰相反,它可使轴承对轴的轴的支撑跨距相对几何中心距增大,从而减小处于两轴承外的载荷对轴造成的挠度(扭曲变形)。
轴只处在上述单一受载情况时,选用“正装”还是“反装”一目了然,即受载位置均在两轴承之间时选用正装,在受载位置在两轴承之外时选用反装。但在实际生产过程中,我们往往会遇到受载位置既在两轴承之间又在两轴承之外的轴,如图2所示二级减速器的输出轴。
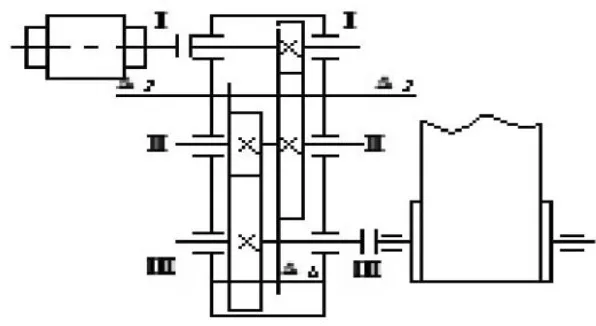
图2 二级减速器示意图
1 建模分析方法
1.1 计算弯矩方程
对目标轴进行受力分析,计算出两轴承支撑处受力后,通过查表或绘图后计算,得到轴上弯矩方程。
1.2 计算转角、挠度方程
根据挠曲线的近似微分方程,由弯矩方程推出轴的挠曲线方程,并由其导数求取极大值点与极大值。
1.3 绘制挠度变化图像
将方程中两轴承间轴段长度与两轴承外轴段长度替换为Ln+x,Lm-x,x<0时为正装,x>0时为反装,规定好x范围,将方程输入maple,使用图像生成器生成直观的图像,观察随着x变化,最大挠度将如何变化。
下面通过实例分析过程得出有关方程和图像。
2 实例分析
2.1 对轴受力情况化简
对于输出轴的受力可以简化为图3。
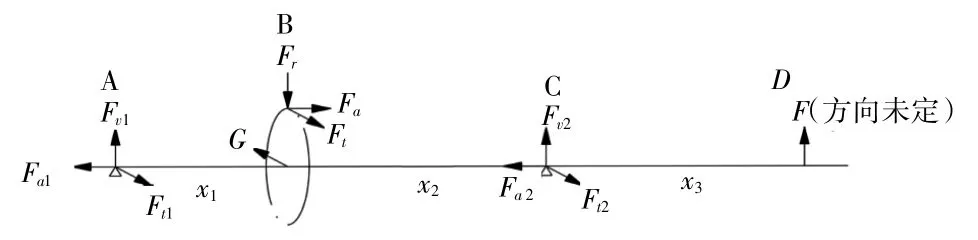
图3 输出轴的受力简图
图3中已知参数见表1。

表1 已知参数
2.2 绘制轴弯矩图,求出各轴段弯矩方程
据此画出轴的弯矩图(图4)。备参数关系见表2。
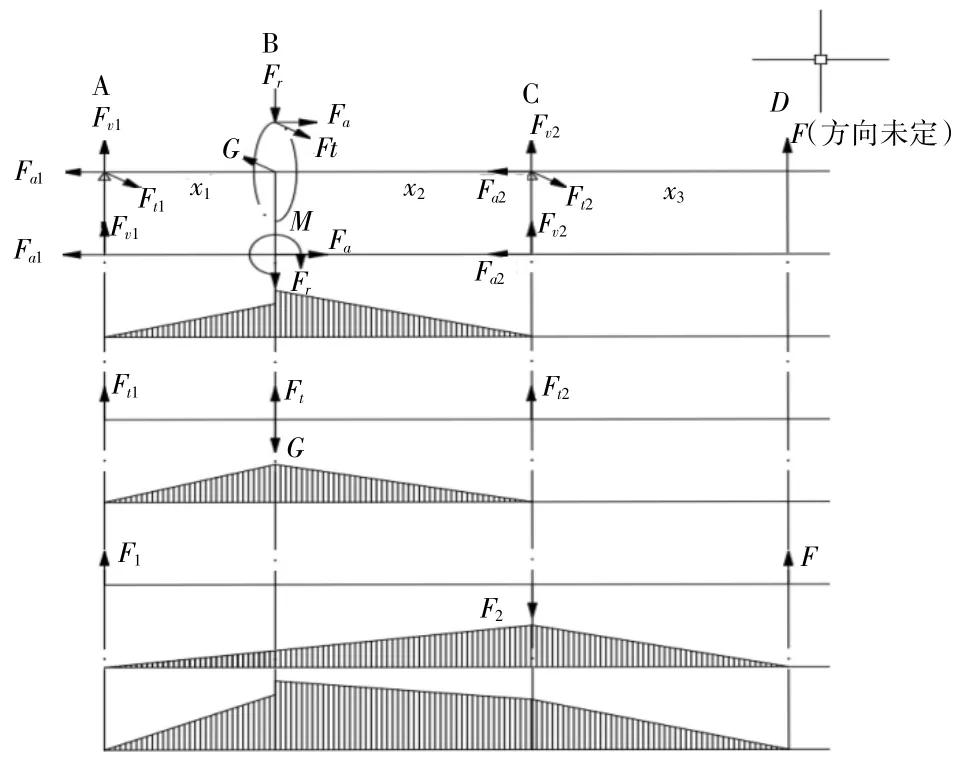
图4 轴的弯矩图
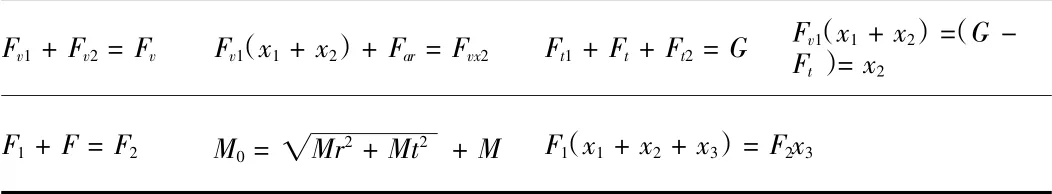
表2 各参数关系
由此可求出m1、m2、m3:

由这3个点可计算出AB、BC、CD段分别的弯矩方程:
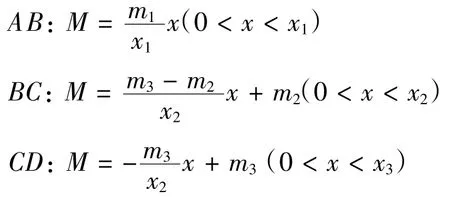
2.3 由弯矩方程计算各轴段挠度与转角方程及极值
根据挠曲线的近似微分方程
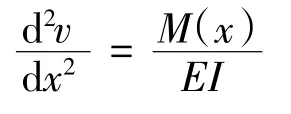
求得各轴段挠度与转角方程:
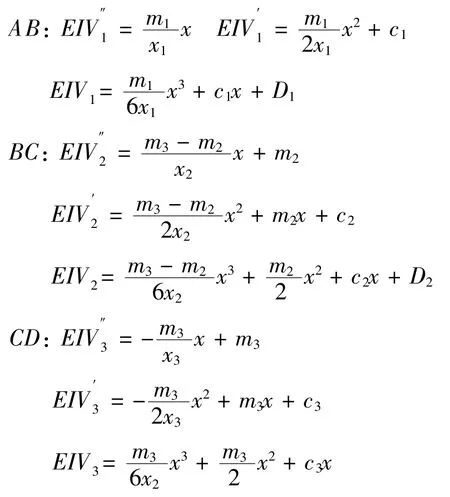
同时由轴系结构可得:左、右轴承处挠度为0,AB段与BC段、BC段与CD段连接处转角与挠度相等,即:
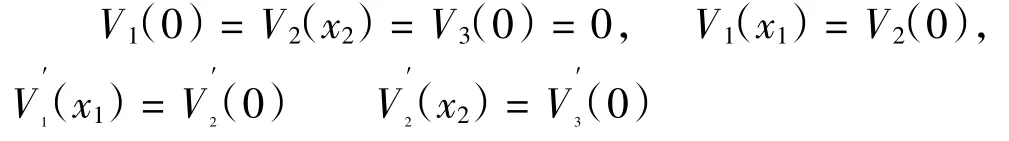
联立可求出
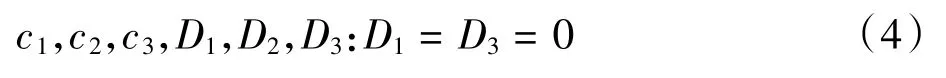

代入方程后,即可通过VI(x)=0求出各轴段的最大挠度vmax。
2.4 代入已知数据进行绘图
已知各轴段长度见表3。
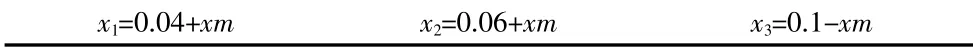
表3 已知各轴段长度
-0.02<x<0.02,使用maple进行计算绘图到图5~图11。
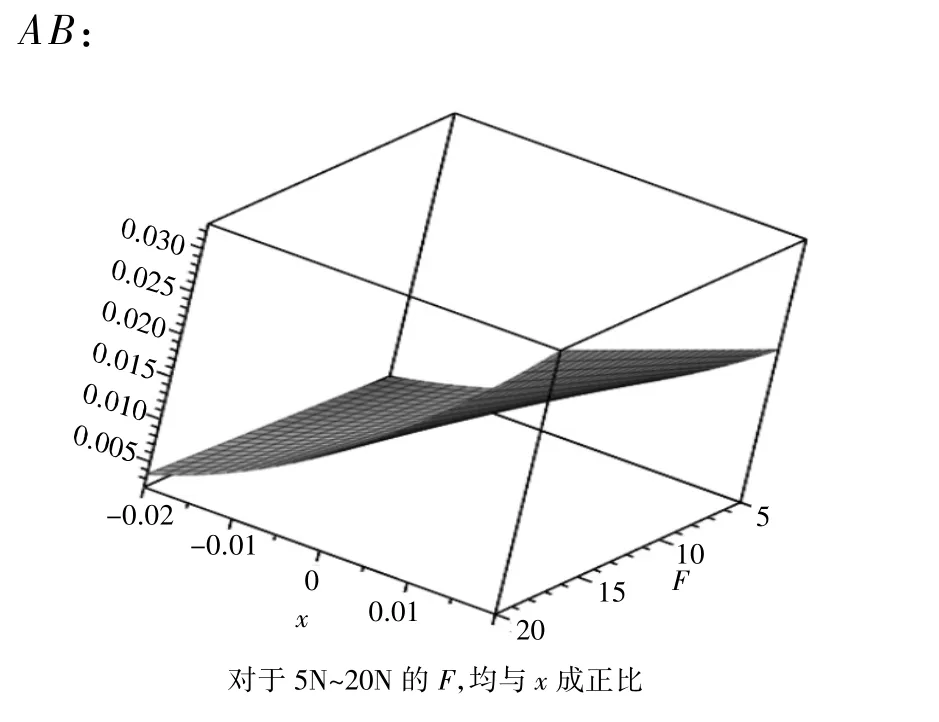
图5 最大挠度(mm)
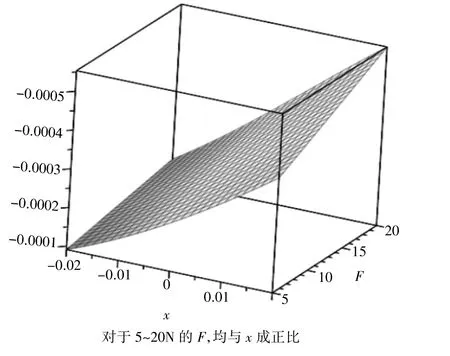
图6 最大转角(轴承处)
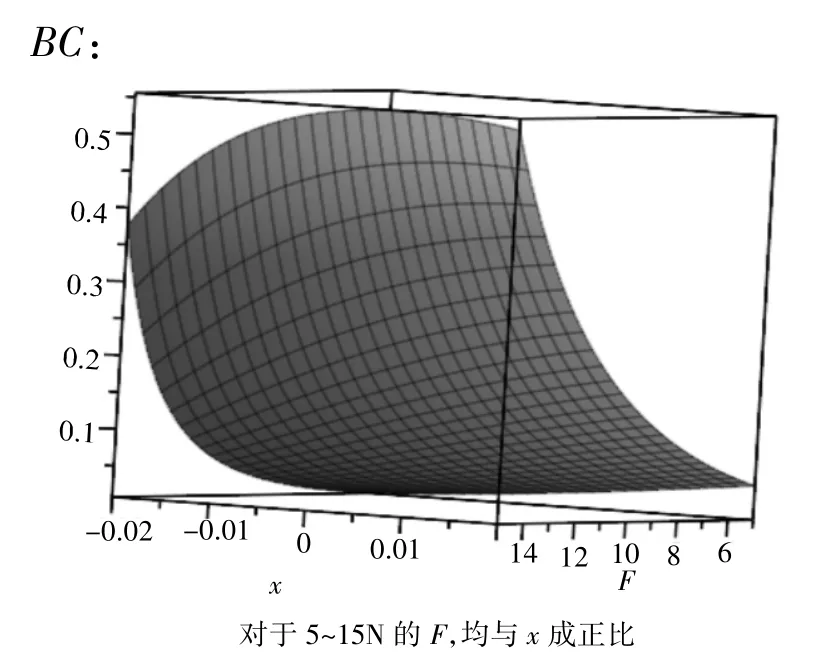
图7 最大挠度(mm)(5N<F<15N)
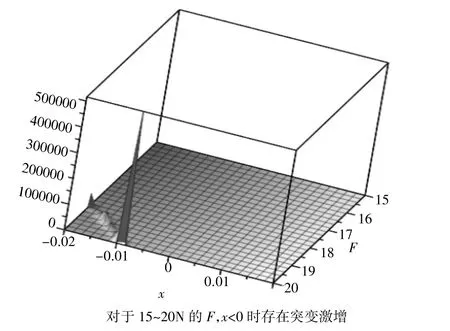
图8 最大挠度(mm)(15N<F<20N)
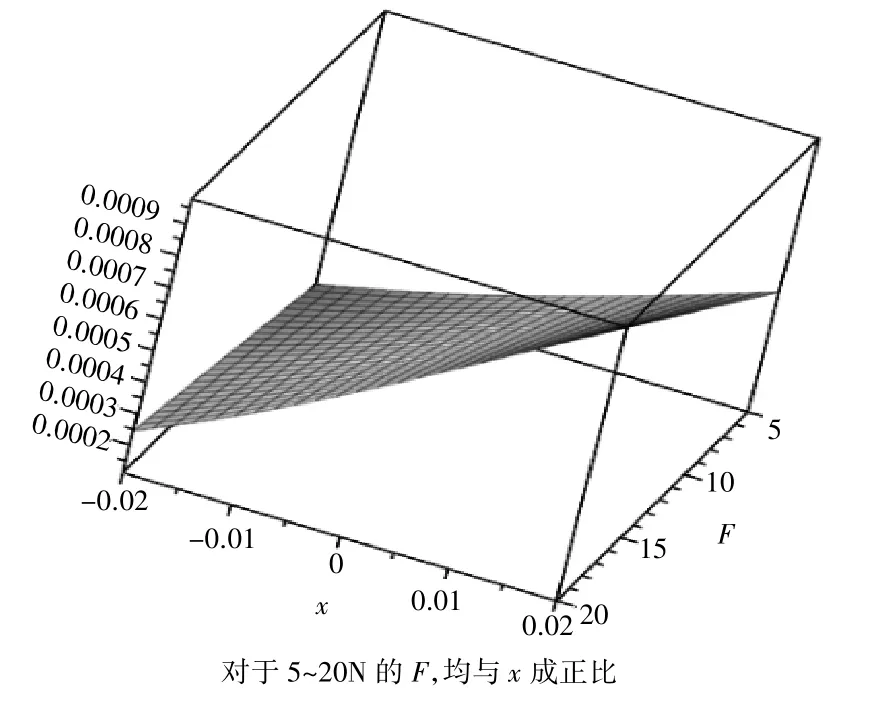
图9 最大转角(轴承处)
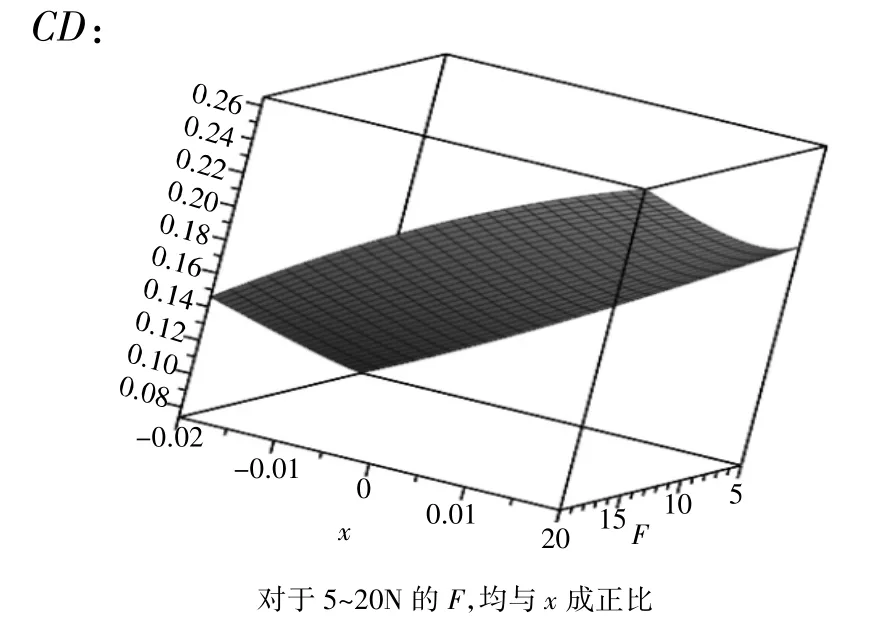
图10 最大挠度(mm)
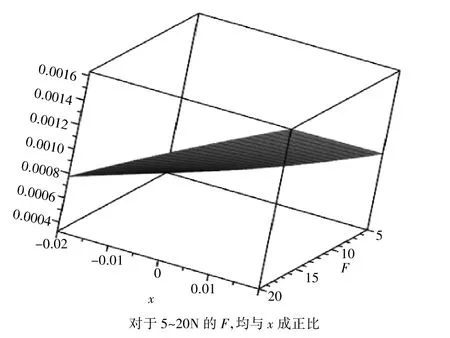
图11 最大转角(皮带轮处)
3 图像分析
从图像可以看出,在两轴承外的受力F处于5~15 N时,AB段,BC段,CD段的最大挠度都随着x减小而减小,在x为负值时达到最小值,同时,两轴承处的转角和两轴承外受F力处转角也都随着x减小而减小,在x为负值时达到最小值;而当两轴承外的受力F处于15~20 N时,AB段,CD段的最大挠度与两轴承处和两轴承外受F力处转角与x的关系不变,BC段最大挠度随着x减小出现突变激增现象。
4 结语
在两轴承外的受力F不远大于两轴承间受力Fr时,应优先选择轴承正装,可有效减小各轴段的挠度以及两轴承处的转角,从而增加轴寿命,传动精度以及减小轴承磨损。其他情况可通过重新构建各轴段的弯矩方程以及更改x1,x2,x3,Fr,Ft,G,F等参数来进行计算判断。
