建筑桩基单桩承载力计算方法分析

王荣菊，杜云晶

（山东聊城市佳汇施工图审查有限公司，山东 聊城 252000）

1 引言

桩基具有优越的承载性能，在提高地基承载力和控制建筑物沉降变形方面具有良好的适用性，并且施工简便、设计简单、经济性强等，在工程项目中被大量使用，并取得了卓越成效[1-2]。但从桩基的安全性角度来讲，桩基础（尤其是桩长较长的桩基）必须经过严格的设计[3-4]。

目前，我国建筑发展如火如荼，桩基承载力的计算分析方法也多种多样。其中，有学者通过现场实验进行分析计算[5-6]，也有学者通过数值分析进行计算，此外，还有理论分析及模型实验等方法。但诸多方法均有其局限性。为探明各方法的适用性及局限性，本文基于数值分析、模型实验及理论计算，对不同桩基的单桩承载力计算方法进行分析，为研究建筑桩基单桩承载力的计算分析提供理论依据。

2 模型试验法

2.1 实验设备

本模型试验是在由两个半圆柱形高强度钢板焊接组成的自制试验箱中进行的。模型钢筒高1.8 m，直径1.2 m，不仅消除了试验边界条件的影响，而且保证了试验刚度条件。试验装置由加载、反应、测量等装置组成，如图1所示。

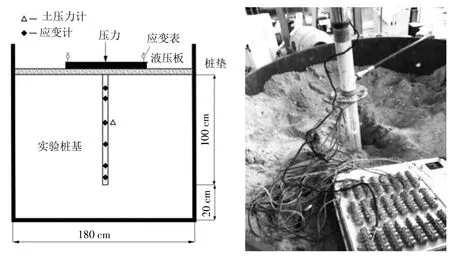
图1 实验装置

2.2 实验材料

2.2.1 土样制备

用于试验的砂土取自位于山东省聊城市某项目场地。所选砂土为颗粒级配较为良好的粉细砂土。在模型试验中，砂土被分层填充并进行人工压实，为了使每层地基土均匀，控制压实厚度，每一层被填充至10 cm，并压实至8 cm。砂土的物理力学参数见表1。

表1 砂土物理和力学参数

2.2.2 模型桩

根据模型试验的缩小规模和桩基材料刚度的相似百分比，本次试验模型桩选择直径50 mm、内壁厚5 mm的空心有机玻璃管。模型桩长度为1.2 m，弹性模量为3.48 GPa。为便于加载，试验中使用的模型桩的实际长度为1.4 m。在试验过程中，模型桩超过试验土体上表面0.2 m。在桩顶和桩底内部均粘贴了应变计，并在试验时测量了桩顶和桩底的轴向力，模型桩如图2所示。

图2 模型桩实物图

2.3 实验过程

在垂直加载单桩承载力模型试验中，采用手动独立的液压千斤顶加载。输出油压采用安装在油路上的油压力计进行测量，并根据压力机上校准的负载-油压力曲线进行控制。在试验过程中，使用固定在桩顶部和底部的应变计实时测量桩顶部和底部的内力。

荷载从0.5 kN开始，每级加载0.5 kN。当桩位移急剧增加时，停止加载。待每级荷载稳定后，前面每隔5 min测量一次，15 min后减缓测量频率，每隔15 min测量一次桩顶的垂直位移，当每根桩的桩顶的沉降小于0.1 mm时，开始下一级荷载加载。

2.4 实验结果

为保证实验结果的可靠性，本实验共选用4根单桩，实验结果如图3所示，从图中可以看出，4根不同桩体的荷载-沉降（Q-S）曲线轨迹基本一致，均呈现出随着桩顶荷载的加大，沉降逐渐增加的趋势，且在加载初期，即当荷载从零开始加载时，桩顶沉降随之发生变化，首先发生细微沉降，大致与荷载增加保持线性关系增长，随后，沉降快速发生，逐渐变得明显，并出现较大的位移。不同的是，对于不同的桩体，由于每次装填土、桩身摩阻力等外界因素的影响，其位移沉降大小略有不同，但对比图4现场实测单桩数据结果可以发现，两者数据较为接近，各模型实验结果与现场实测数据误差均在误差影响范围之内，由此可见，模型实验能够最大限度地反映现场桩基的承载情况。

图3 模型实验所测单桩Q-S曲线

图4 现场实测单桩Q-S曲线

3 数值计算法

3.1 计算模型及参数

本文数值模型计算使用软件为Midas/GTS，该软件不仅能提供完整的三维动态分析和各种本构模型，还被证实能适用于大型变形计算，目前国内大多数设计院中也将此软件用于模拟计算单桩承载能力。计算时，为尽量还原桩承载的实际状况，一般模型计算中的桩侧土视为理想弹塑性材料，将桩视为线性相关材料，并假以摩尔-库伦准则。

3.2 计算过程分析

在数值模型计算时，由于参数及桩基的模型均为定值，因此，无须重复实验，故本模型计算只需对单根桩基进行一次模拟实验便可，模型计算时荷载加载方式仍按照模型实验加载方式进行。考虑平面影响范围约为2.5倍桩径，模型底部影响深度约为3倍入土深度，则有限元模型尺寸为4.5 m×3.6 m。模型共有154 996个块体单元，35 724个结点。有限元计算模型网格划分如图5所示。

图5 计算模型和网格划分图

3.3 模型选用的本构模型

3.3.1 弹塑性模型

由于单桩为钢筋混凝土桩，故采用弹性理论进行计算，弹性变形通常采用广义胡克定律进行计算。广义胡克定律计算公式为：

式中，dσij为应力增量，kN；dεkl为应变增量，mm；为弹性模量张量，kN/mm。

3.3.2 屈服准则

旧词新义是指把英语中原有的词汇赋予新的含义成为语义新词。赋予新义的旧词起初只用于英语口语中，后来，根据约定俗成的原则逐渐广泛地用于科技词汇中。大部分词的新义与原义有着某种明显的联系，如：

由上述内容可知，模型模拟材料选取为Mohr-Coulomb材料，故选取Mohr-Coulomb屈服准则作为材料的破坏准则，屈服函数表达式如下：

式中，σ1、σ2、σ3为主应力，其中，σ1＞σ2＞σ3；φ为土体内摩擦角；c为黏聚力。

3.4 模型计算结果

经数值模型计算，得到荷载沉降曲线图如图6所示，从图中可以看出，数值模型计算荷载沉降结果与模型实验结果略有差距，但荷载沉降曲线趋势与模型实验基本吻合。加载初期，由于土体设置为弹塑性特性，故开始表现出一定的弹性变形，但在后期，由于变形发展，土体逐渐向塑性变化，呈现曲线发展，由此不难看出，数值计算结果与模型实验基本一致，故可以作为建筑桩基承载力的计算方法的一种。

图6 数值模型所得单桩Q-S曲线

4 理论计算法

由工程资料可知，本文工程研究对象主体结构桩基均设计为单桩形式，桩基设计采用挖孔成桩，因此，在进行理论计算时，采用相关规范推荐公式进行计算。

式中，[P]为单桩轴向受压容许承载力，kN；U为桩的周长，m；l为桩在局部冲刷线以下的有效长度，m；A为桩底横截面面积，m2；τp为桩壁土的平均极限摩阻力，kPa，可按式（4）计算：

式中，n为土层的层数；li为承台底面或局部冲刷线以下各个图层的厚度，m；τi为与对应各土层与桩壁的极限摩阻力，kPa；σR为桩尖处土的极限承载力，kPa，可按式（5）计算：

式中，m0为清底系数；λ为修正系数；k2为承载力特征值的深度修正系数；γ2为桩端以上各土层的加权平均重度，kN/m3；h为桩端的埋置深度，m；[σ0]为桩尖土的允许承载力，kPa。

综上，公式及地质资料计算可得桩基拱顶沉降变形数据如图7所示。可以看出，采用理论公式法计算桩顶荷载-沉降曲线呈现明显的两阶段变化，开始阶段隧道弹性变形较为明显，此阶段与数值分析计算相近，但较实测却有所偏差，第二阶段出现急剧下降，存在明显的转折点，可知理论法计算较实际偏差较大，相比于前两种计算方法，采用理论法计算桩基承载力不仅计算复杂，且结果偏差较大。由此可见，理论计算法局限性较高，对于工程地质条件复杂下的桩基，不适于理论计算法分析研究。

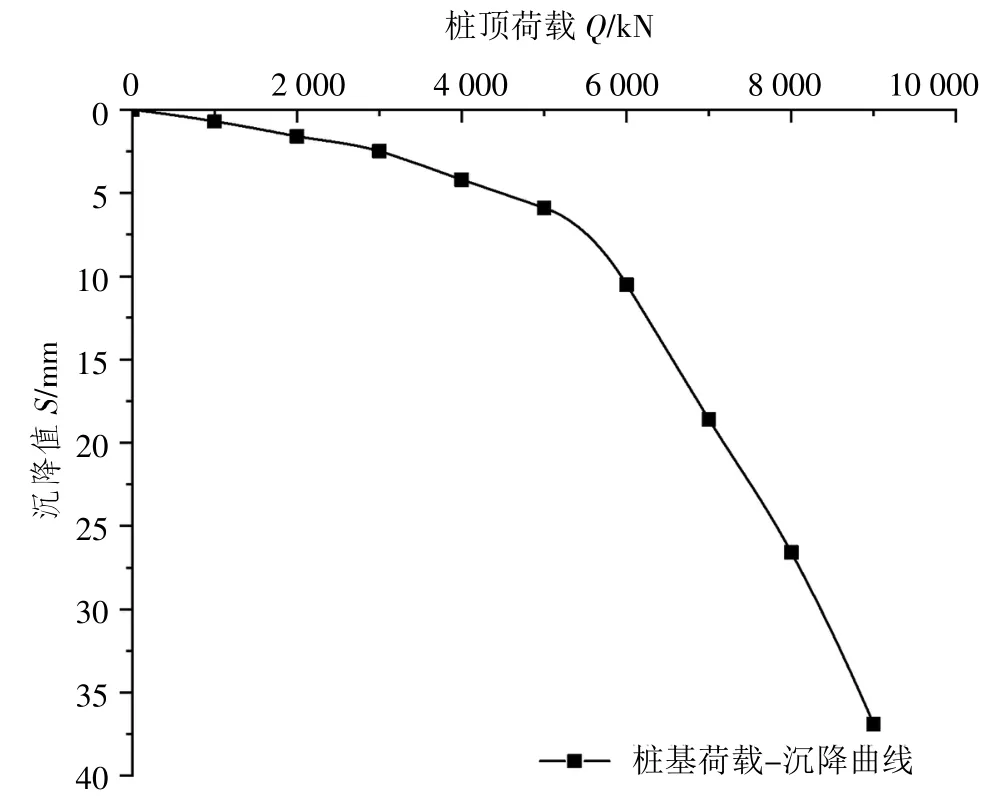
图7 理论法计算所得单桩Q-S曲线

综上不同计算建筑桩基单桩承载力计算方法分析可知，在建筑桩基单桩承载能力计算中，不同计算方法的适用性各有不同，但总体而言，模型实验最为贴近现场环境，其计算准确率也最高，是建筑桩基单桩承载力计算方法的理想模型，其次便是数值计算，理论计算仅作为模型验证及分析使用。

5 结论

本研究基于模型实验、数值计算及理论近似解的基础，分析了3种不同单桩承载力计算方法对建筑桩基单桩承载力计算结果的准确度的影响，得出以下结论：

1）基于本文现场实测桩基沉降变形数据发现，模型实验计算结果最接近于现场实测真实值，由此可见，模型实验最能反映现场真实情况，因此，在经济允许的条件下，为能够准确反应现场情况，宜进行模型实验。

2）基于数值分析结果可以得出，数值分析计算在某种程度上分析桩基沉降变形规律，对于桩基变形的弹性阶段及塑性阶段均可明显反应在变形曲线上，可以作为桩基沉降变形计算及极限承载能力判别的辅助工具。

3）基于理论计算分析结果可以得出，理论计算较前两种计算方法有较大的局限性，计算结果虽然较数值分析计算更加准确，但计算过程却较为复杂，使用范围较为局限。但理论计算却可以弥补数值分析及模型实验计算理论性不足的缺点。