装配式剪力墙等效斜撑模型研究
2022-10-20邓亚军刘正雄郭智刚金奇峰
邓亚军,刘正雄,郭智刚,金奇峰
(1.深圳市市政工程总公司 深圳 518000;2.武汉理工大学土木工程与建筑学院,武汉 430070)
近年来,随着我国经济的发展和节能减排工作深入进行,装配式建筑以其特有的污染少、建造速度快等优点,在与传统现浇式建筑结构的竞争中脱颖而出,而欧美等发达国家已经形成了系统的装配式结构的设计理念、构件生产制作和施工成熟的成套体系。预制装配式在当今工业化时代具有进一步深入发展和创新的巨大潜力。现阶段,针对装配式框架节点的研究已经逐步成熟,连接方式和施工工艺已形成较多的规范规程,装配式建筑体系也逐渐丰富,功能更加齐全[1]。但对受力性能较为复杂的装配式混凝土墙板结构的力学性能、设计与构造的方法以及工作原理等理论的研究还不足,也缺乏适用于一般工程分析计算的等效计算公式。因此,为方便地进行装配式剪力墙的分析计算,提出一种将剪力墙等效为斜撑的分析模型,基于此分析模型,提出了拟合的计算公式,以方便地进行等效的分析计算。
通过对实验现象的观察,装配式剪力墙破坏的特征是在对角线附近出现斜向开裂,主要特征是在对角线附近出现斜向开裂,破坏从一墙角延伸到另一墙角,最终墙角区被压碎。这种模式,形成了斜压传力机制。国外部分学者对此已经进行了一定的研究,如1999年的Roger D F[2]、2003年的El-Dakhakhni[3]根据各自的研究,均提出了有一定使用范围的计算公式,而美国联邦应急管理署提出的《建筑物抗震加固预标准及评述(FEMA356)》中也提到计算等效支撑的宽度的公式[4],但国内对此的研究尚有较多不足。同时,相对传统墙体装配式剪力墙在侧向荷载作用下更容易产生整体转动。传统的斜撑宽度计算公式已经不再适用于装配式剪力墙,因此,文章将利用Opensees有限元分析软件,建立合理的分析模型后,提出基于FEMA356的改进计算公式,并在不同的条件下验证公式的正确性。
1 分析模型的建立和公式的提出
利用OpenSees分析平台,建立两种模型:模型1是原始参照的接触模型,模型2为简化分析计算模型。模型1采用梁柱节点单元来模拟梁柱节点,剪力墙使用分离式建模,使用quad模拟混凝土,用桁架单元模拟钢筋,混凝土和钢筋之间通过共同使用的节点连接,协调变形。在剪力墙和柱之间设有接触单元zeroLengthInterface2D单元,用来模拟剪力墙板与柱之间的接触[5];剪力墙下部设有弹簧,用truss单元模拟弹簧。为了更好地模拟剪力墙的受力性能,在模拟弹簧时,truss单元使用单压材料,使此处的弹簧,只能承受压力,不能承受拉力;在每个柱底都设有零长度截面单元,来模拟柱底钢筋的滑移,定义建立起与柱之间的库伦摩擦因数为0.36。模型单元如图1所示。
模型2为等效斜撑模型,如图2所示,用梁柱纤维单元模拟梁与柱,框架的建模过程与接触模型的建模过程相同,斜撑为混凝土材料的桁架单元,采用Concrete01本构模型,只能承受压力作用。在往复循环加载过程中,一片应简化为两个交叉的斜撑,且斜撑只能承受压力作用,考虑研究为单调加载,墙承受的是斜压作用,故简化为一个撑的作用,具体分析采用嵌入式剪力墙,梁不对斜撑有约束作用,故斜撑顶部与柱的连接点并非是梁柱节点,而是在墙高处将斜撑与柱铰接。

等效斜撑模型中斜撑宽度是最重要的参数,通过有限元模拟发现斜撑宽度与墙体对角线的长度成正比,FEMA356中则提出斜撑的计算公式
ω=0.175(λh)-0.4d
(1)
但该公式存在计算不够准确、受不同条件影响结果离散性较大等缺陷,利用分析模型对此公式进行修正。以跨高比为基本参数,选取跨高比为1.0和2.0进行拟合,并遵循初始刚度相同和结构强度相同的原则,对接触模型进行单调加载,得到顶点的荷载-位移曲线,并以此为参考,找到斜撑模型单调加载下与参考曲线吻合的宽度,并记录此宽度ω。

在跨高比等于1.0时,选取L=2 335 mm、H=2 335 mm进行分析,对接触模型与斜撑模型在同一边柱柱顶进行单调位移加载,得到接触模型与不同斜撑宽度下的荷载-位移曲线,如图3所示。根据斜撑模型与接触模型在相同荷载作用下初始刚度相等以及结构强度相同的原则,可以得出等效斜撑的宽度应取为38 mm。在跨高比等于2.0时,选取L=1 550 mm、H=3 100 mm进行分析,对接触模型与斜撑模型在同一边柱柱顶进行单调位移加载,得到接触模型与不同斜撑宽度下的荷载-位移曲线,如图4所示。根据斜撑模型与接触模型在同荷载作用下初始刚度相等和结构强度相同的原则,可以得出等效斜撑的宽度应取为28 mm。
按上述方法,利用OpenSees分析平台,依次得到跨高比为1.0与2.0情况下的ω值,并将得到的ω/d作为Y坐标值,λh作为X坐标值放在同一直角坐标系中,得到跨高比为1.0与2.0情况下一系列的分布点,如图5所示。
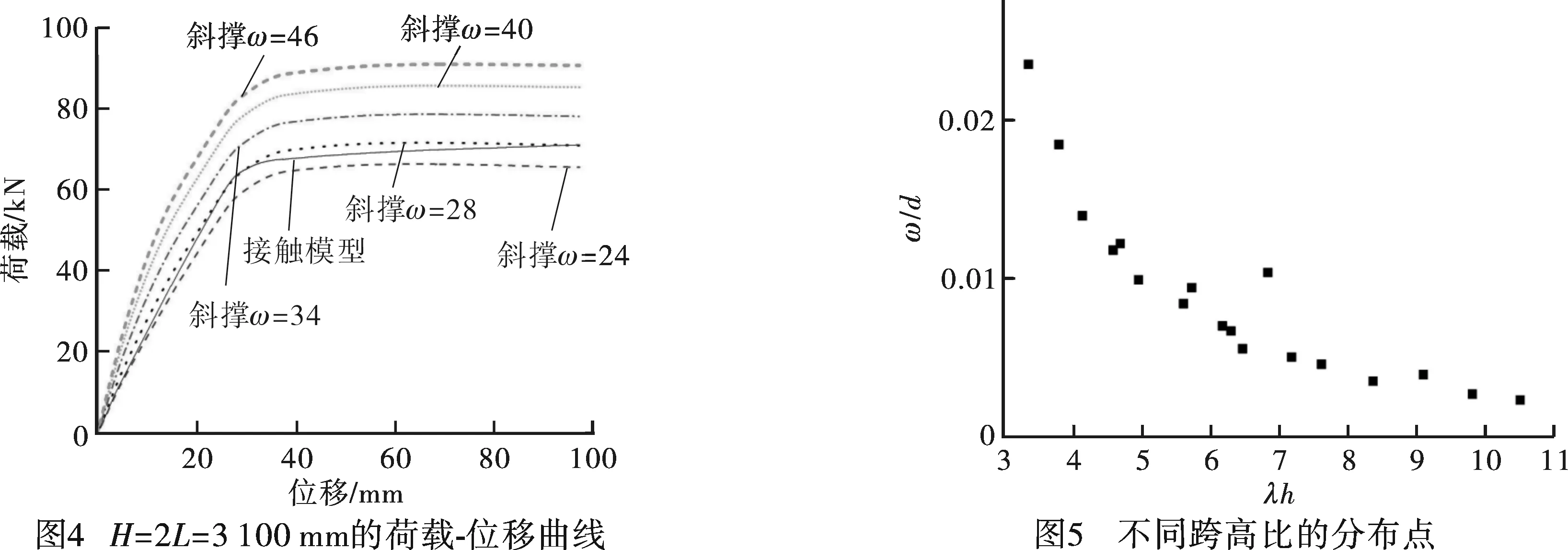
通过对上述分布点进行公式拟合,可以得到无开洞剪力墙等效斜撑宽度的改进计算公式(2)。
ω=1.5×0.175(λhw)-2d=0.263(λhw)-2d
(2)
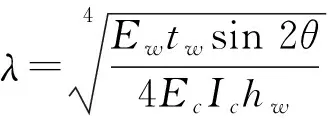
2 不同条件下公式的验证
1)跨高比对公式的影响
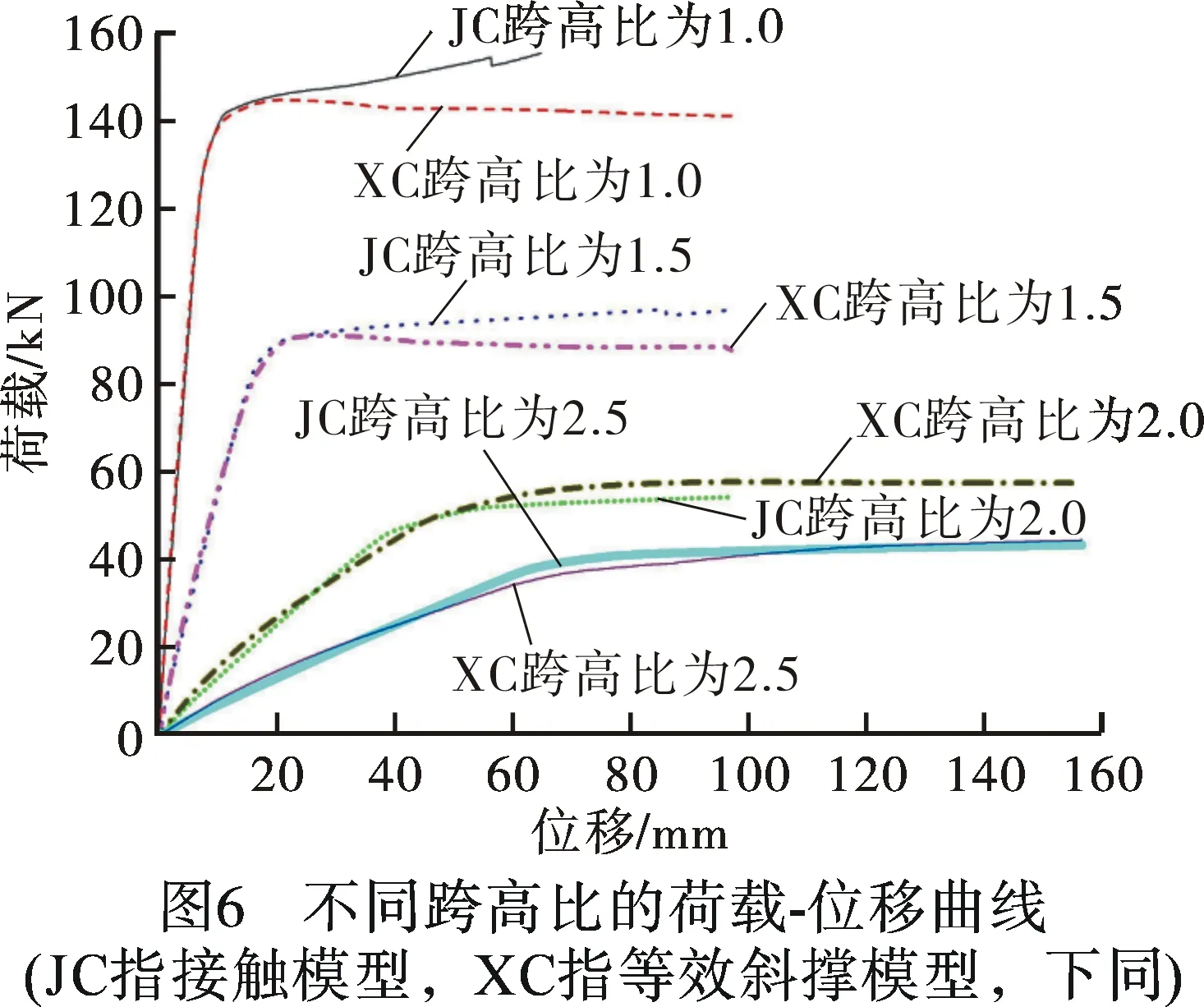
验证不同跨高比下公式的实用性,选取跨高比为1.0、1.5、2.0及2.5四种情况进行验证,并对接触模型和等效斜撑模型进行单调位移加载,得到四种情况下接触模型和等效斜撑模型顶点的荷载-位移曲线,如图6所示。通过对接触模型和等效斜撑模型的顶点荷载-位移曲线对比分析可知,拟合出的防护墙等效斜撑公式可适用于不同跨高比下等效斜撑宽度的计算。
2)墙板厚度对公式的影响
公式拟合是在剪力墙厚度为50 mm的条件下进行的,为了验证不同剪力墙厚度下公式的适用性,取剪力墙厚度为80 mm、100 mm、120 mm三种情况进行讨论,取试验的一榀两跨结构进行模拟,其中跨度为1 550 mm,高度2 335 mm。通过不同墙板厚度条件下结构的荷载-位移曲线的对比可知(如图7所示),接触模型与等效斜撑模型有较好的吻合度,说明在墙板厚度不同时,等效斜撑宽度的计算公式仍然适用。
3)轴压比对公式的影响
选取柱子轴压比为0.1、0.2和0.3三种情况,验证不同竖向荷载下公式是否适用。选取一榀两跨结构,其中跨度为1 550 mm、高度为2 335 mm。单调加载后的顶点位移曲线如图8~图10所示。在不同轴压比下,等效斜撑模型与接触模型较好的吻合,其中等效斜撑的宽度是通过前面拟合公式计算得到的,说明等效斜撑宽度的计算公式不受轴压比的影响,即拟合得到计算等效斜撑宽度的公式在施加不同的竖向荷载下同样适用。


3 结 论
通过对装配式剪力墙结构试验破坏过程的分析,建立了合理的等效斜撑模型,基于分析拟合出无开洞装配式剪力墙的等效斜撑的宽度计算公式。分别在不同跨高比、不同墙板厚度和不同轴压比的情况下对拟合公式进行验算。在此三种典型的情况下,公式计算结果和分析结果吻合程度良好,验证了公式广泛的适应性。该公式可以针对仅承压的等效斜撑模型宽度进行准确评估,从而简化分析过程,方便工程应用。
