一类浮游植物模型的分支分析
2022-10-20王立叶杨瑞智
王立叶, 杨瑞智
(东北林业大学 理学院, 黑龙江 哈尔滨 150040)
水体富有营养化引起藻类和浮游植物大量繁殖,形成水华,造成水质污染,控制甚至解决水华问题不容忽视。除了生物法以及藻华防控技术等方法[1-4],学者们还构建并研究了许多浮游植物模型并取得了丰富的研究成果。文献[5]研究了物质循环和状态反馈控制下的营养-浮游植物模型,文献[6]分析了具趋化的浮游动植物模型,文献[7]探究了非退化扩散和退化扩散下的随机浮游动植物模型。本文考虑到由于营养物质和浮游植物在空间分布是不均匀的,并且会产生扩散现象,故在文献[8]已有的浮游植物模型的基础上加入扩散项,研究了带扩散的浮游植物模型,其数学模型如下所示:
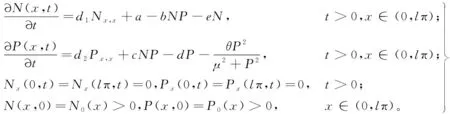
(1)
式中:x是空间变量;t是时间变量;d1和d2分别表示营养物质和浮游植物的扩散系数;Nx和Px分别表示N和P对x的一阶导数;Nx,x和Px,x分别表示N和P对x的二阶导数;N表示营养物质的浓度;P表示浮游植物的数量;a表示持续的外在营养物质的注入;b表示浮游植物对营养物质的最大吸收速率;c表示营养物质到浮游植物的最大转变速率;d表示浮游植物的平均死亡速度;e表示营养物质的平均损失率;θ表示产毒浮游植物释放有毒的化学物质的速率;μ表示半饱和常量。
1 稳定性分析
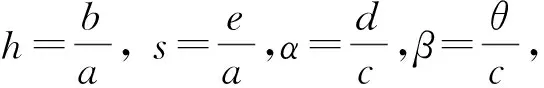
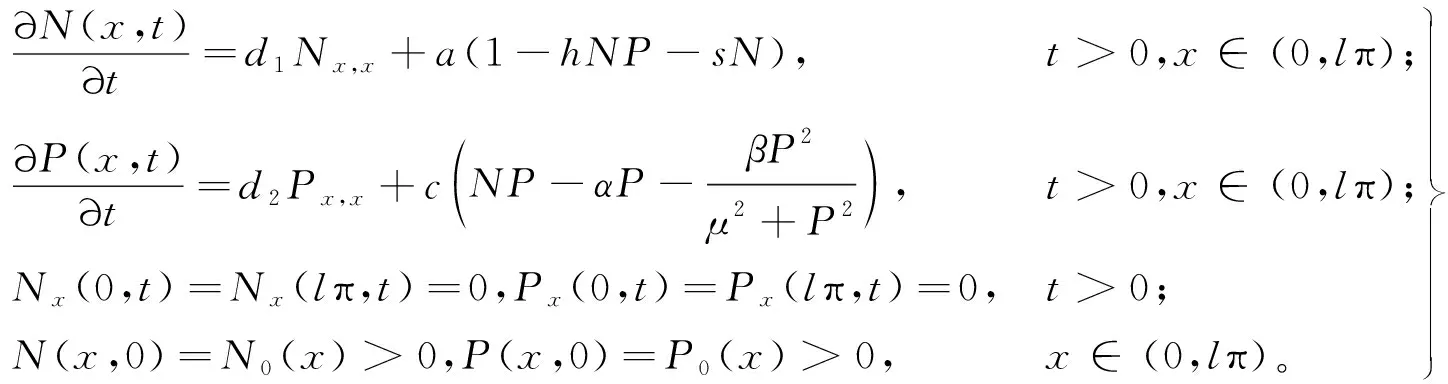
(2)
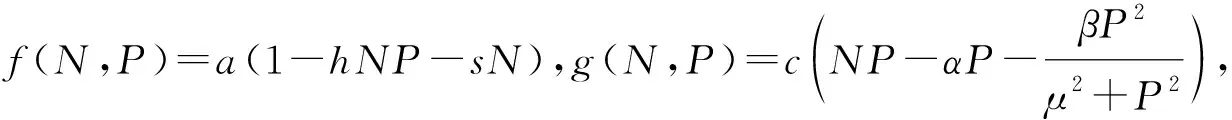
hαP3+(hβ-(1-sα))P2+(sβ+hμ2α)P-μ2(1-sα)=0。
(3)
P*为式(3)的解。
定理1 若1-sα≤0,则系统(2)没有正平衡解;若0<1-sα≤hβ,则系统只有1个正平衡解;若hβ<1-sα,则系统有1个或3个正平衡解。
系统(2)在正平衡解E*处的雅可比矩阵为

λ2-Tr(J)λ+Det(J)=0。
(4)
式中:Tr(J)=b2-a1;Det(J)=a2b1-a1b2。则当条件H1(b2-a1<0,a2b1-a1b2>0)满足时,式(4)有2个具有负实部的根,即系统(2)的正平衡解E*局部渐近稳定。
2 Turing不稳定性分析
利用反应扩散方程理论,可以得到反应扩散系统(2)在正平衡解E*处的特征方程为
令z=(n/l)2,可化为
λ2-Tnλ+Dn=0,(n=0,1,2,…)。
(5)
式中:Tn=-(d1+d2)z-a1+b2;Dn=d1d2z2+(a1d2-b2d1)z+a2b1-a1b2。
根据文献[9],若想使E*不稳定,式(5)至少有1个实部为正的特征根。

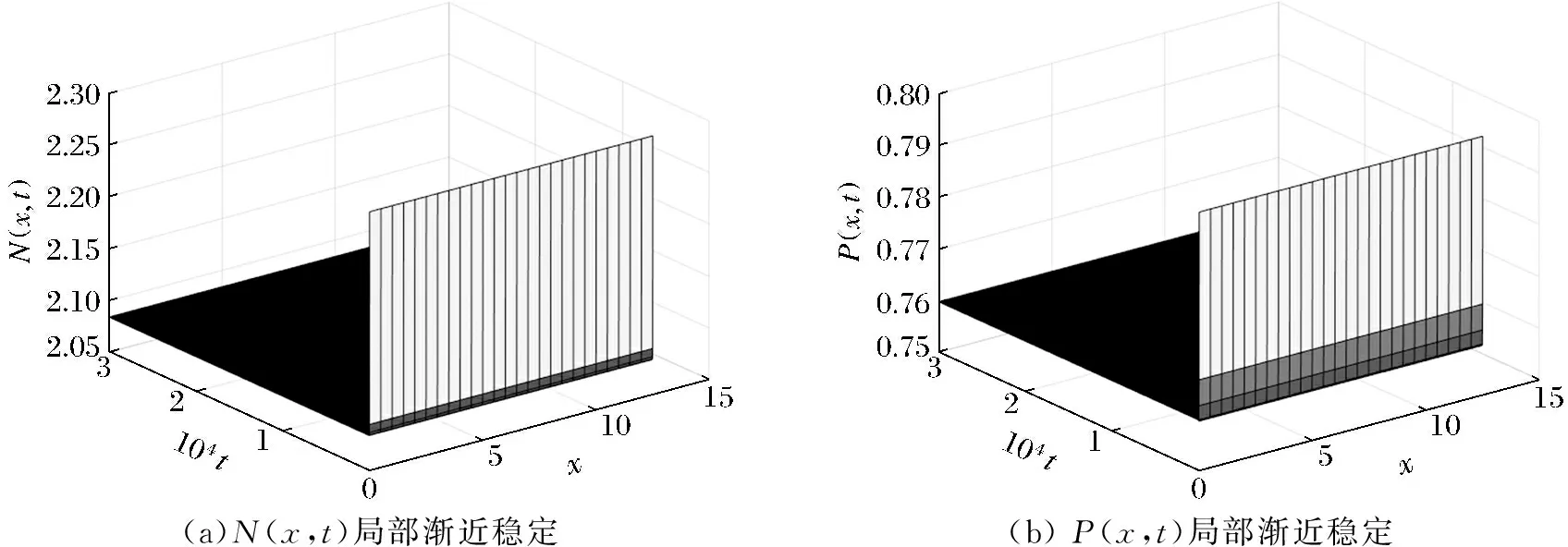
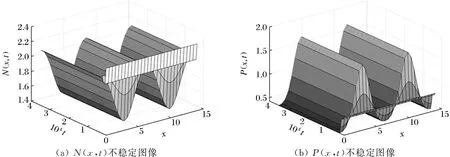
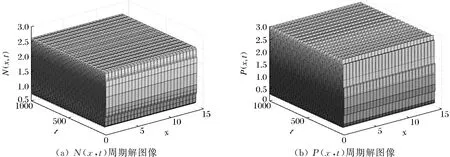
证明 令D(z)=0有2个根分别为z1,2且z1 在这一部分选取a为分支参数。部分公式来源于文献[10]。由Tn=0,得到关于参数a的一系列临界值 取条件H3(①b2d1-a1d2<0;②b2d1-a1d2>0且Δ<0;③b2d1-a1d2>0,Δ>0且z∉(z1,z2))。 引理1 当a=a(n),(n=0,1,2,…)时,Tn=0,若满足条件H3中的任意一条时,都有Dn>0,此时式(4)有1对纯虚根。 定理3 若条件H3中任意一条成立,当a=a(n)(n=0,1,2,…)时,系统(2)在E*附近产生Hopf分支。 接下来,将对Hopf分支的性质进行分析,为了方便,只给出了在a=a(0)时决定Hopf分支的性质的参数计算公式。 系统(2)在E*附近的特征方程记为L(a),L*(a)为算子L(a)的共轭算子。 可得 当a=a(0)时,可得 其中: 当Re(c1(a(0)))<0(>0)时,Hopf分支是向后的(向前的),并且分支周期解是局部渐近稳定的(不稳定的)。 令Ω=(0,4.5π),h=0.5,s=0.1,α=0.247,β=2.0,μ=0.5,c=1.0。计算得系统的正平衡解为(N*,P*)≈(2.084,0.76)。 在常微分方程系统中d1=d2=0,取a=2.098,其余参数保持一致,则有a1>b2,a2b1-a1b2=0.929>0,满足条件H1,所以系统(2)的正平衡解为局部渐近稳定,如图1所示。选取参数d1=0.004,d2=0.002,偏微分状态下系统(2)的正平衡解是局部渐近稳定的,见图2所示。 图1 系统正平衡解局部渐近稳定Fig.1 Locally asymptotically stable of the positive equilibrium solution of the system (a)N(x,t)局部渐近稳定(b) P(x,t)局部渐近稳定 重新选取参数d1=3.0,d2=0.3,解得z1=0.805,z2=1.283。取n=5时有z∈(0.805,1.283)使Dn<0。即满足产生Turing不稳定的条件,所以系统(2)在E*处产生Turing不稳定,如图3所示。 (a) N(x,t)不稳定图像(b) P(x,t)不稳定图像 选取参数d1=0.001,d2=0.004,a=0.8,其余参数保持一致。计算可得Re(c1(a(0)))=-0.052 1<0,因此系统(2)在E*处有稳定的周期解,如图4所示。 (a) N(x,t)周期解图像(b) P(x,t)周期解图像 本文研究了模型的稳定点存在的条件以及稳定点稳定性的分析。得出:当条件H1成立时,正平衡解是稳定的;当条件H1、H2同时成立时,正平衡解是Turing不稳定的;若条件H3中任意一条成立,当a=a(n)(n=0,1,2,…)时,系统(2)在E*附近产生Hopf分支。3 Hopf分支分析
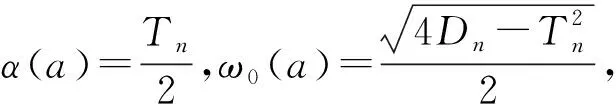

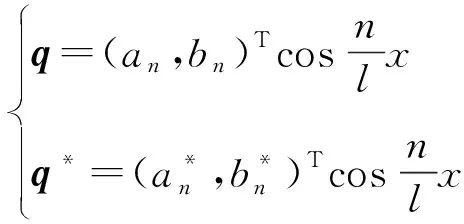
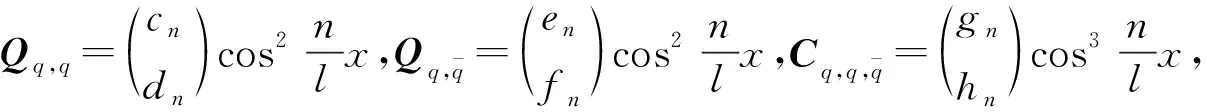
4 数值模拟
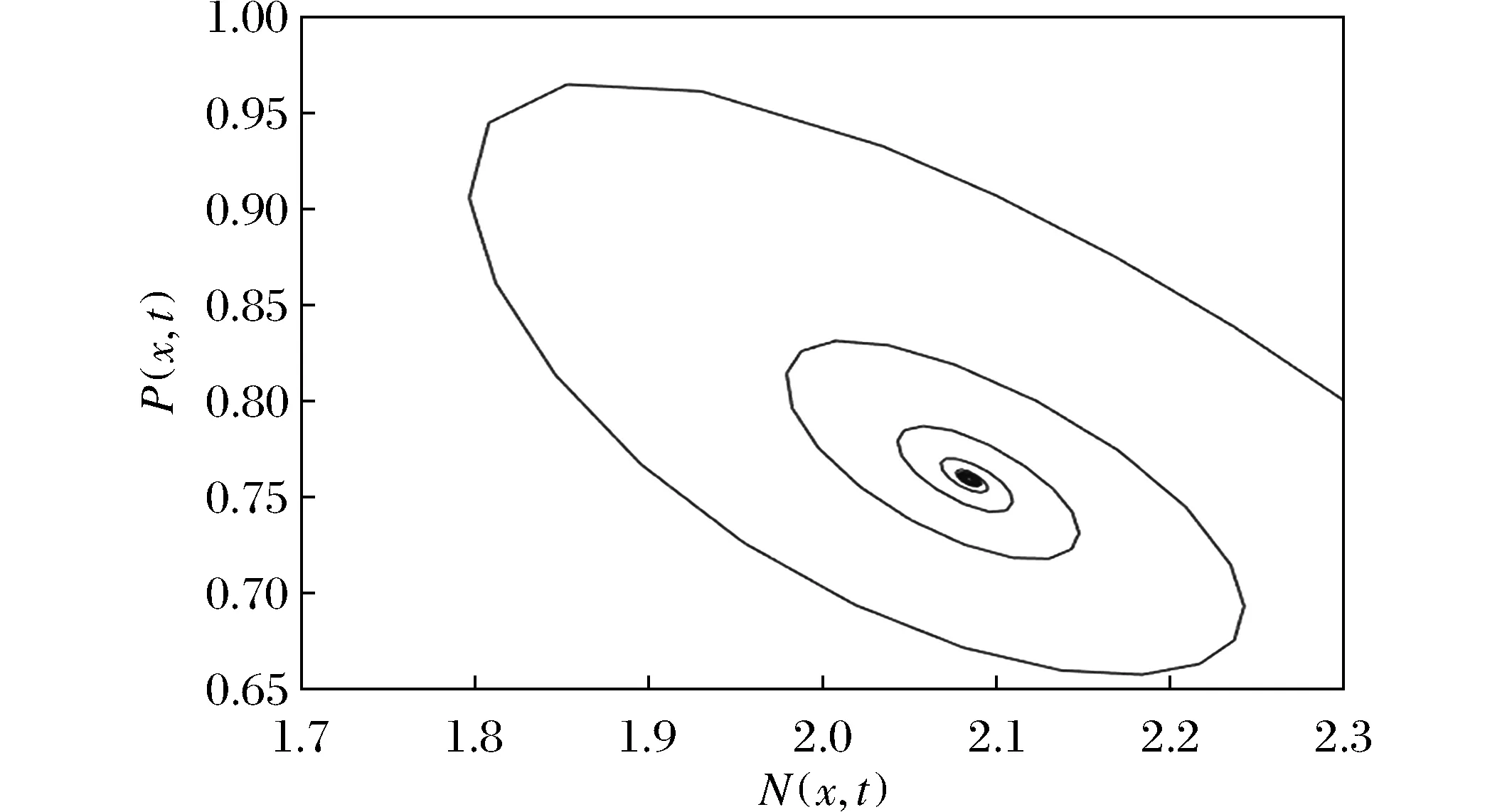
5 结 论
