改进的粗糙集双边滤波图像去噪算法

张雪峰, 万鹏程

(东北大学 理学院, 辽宁 沈阳 110819)

图像在生成和传输的过程中经常因为受到各种噪声的干扰而变质,这对后续图像的处理和图像视觉效果将产生不利影响。因此,在图像处理的过程中,首先要选择一个合适有效的去噪方法[1-2],能够在去除图像目标和背景中噪声的同时保留更多的图像细节信息。

图像滤波,即在尽可能保留图像细节特征的条件下对图像的噪声进行抑制。滤波可分为2大类:线性滤波和非线性滤波。线性滤波主要包括均值滤波、高斯滤波等,线性滤波虽然容易实现,但在去噪的同时可能会导致图像的边缘细节丢失,结果往往并不理想。非线性滤波在对图像去噪的过程中能够保留图像信号的高频细节,因此得到广泛地应用。目前学者们已提出了许多非线性滤波算法:双边滤波[3]是一种常见的非线性滤波,由Tomasi等在1998年提出,其本质是基于高斯滤波,在处理过程中同时考虑到空域信息和灰度相似性,将图像的空间域信息和灰度域信息进行非线性组合,相比于高斯滤波更能保持图像的边缘;引导滤波算法[4]是在双边滤波基础上发展而来的,其将引导图像的结构转化为滤波输出,具有保持边缘的特性;各向异性扩散[5]克服了高斯模糊的缺陷,将像素看作热流,根据当前像素和周围像素的关系,来确定是否向周围扩散,同样保留了图像的边缘。

近年来,许多相关研究人员对双边滤波器的改进做了大量研究。文献[6]提出了一种分类选优的双边滤波算法,从相邻像素集内选择类别结构最相似的像素组成新的相邻像素集,确保新的相邻像素集中用于加权平均的相邻像素尽可能相似,以提高滤波器提取图像特征的效果。文献[7]通过在传统双边滤波模板中加入了补偿函数,进而锐化图像和消除噪声,并利用Thiele型连分式逼近双边滤波器中的指数函数,使双边滤波器易于硬件实现。文献[8]根据滤波窗口内的噪声标准差自适应地调整双边滤波器中的灰度标准差,同时利用中值滤波去除判定出来的强噪声,从而保持图像的清晰度。

本文算法从对滤波器自身结构进行改变的角度出发,基于粗糙集方法,在传统双边滤波模板已有2个高斯滤波核的基础上,加入了一个新的滤波核。首先,对分割子块大小自适应,并通过结合粗糙集在图像中应用于目标和背景区域的上下近似得到优化阈值。然后通过颗粒寻找图像的边界,通过比较颗粒内像素与优化阈值的大小关系,内部大小关系不均匀的颗粒被视为包含目标的边界,再通过像素与阈值的比较对像素进行分类。最后,根据像素之间的类别关系和像素是否在边界颗粒内,分配新的滤波核中的权重,完成对滤波器的改进。本文设计的改进滤波器能够在去除噪声的同时增强图像的边缘,保留更多的纹理细节。

1 预备知识

1.1 双边滤波器

双边滤波器[9]是在高斯滤波器的基础上,考虑了滤波模板中像素灰度值上的相似性,将空间域权重和灰度域权重进行非线性组合,形成新的权重值,将新的滤波模板与噪声图像进行卷积操作得到去噪后的图像。

双边滤波器可定义如下:

式中:Ω为中心邻域内像素点的坐标集合;f(i,j)为当前像素点(i,j)的像素值;f(m,n)为中心点(m,n)的像素值;F(m,n)为滤波后中心点(m,n)的像素值;ωs和ωr别为滤波模板在(i,j)处的空间域权重和灰度域权重;σs和σr分别为空间域标准差和灰度域标准差。可以看出,双边滤波器的核函数是空间域核和像素域核的综合结果。

1.2 粗糙集方法

粗糙集由波兰学者Pawlak[10]在1982年提出,是一套用来研究不完整数据,不精确知识的表达、学习和归纳的理论。它是一种新的处理模糊和不确定性问题的数学工具,该理论能够仅依据观测数据,分析和推理一些不完整信息,发现隐含的知识,揭示数据间的潜在规律。由于粗糙集方法在处理不确定信息时,具有不需要提供任何先验信息的特点,因而在针对不确定性问题的描述和处理时较常规方法更具客观性[11]。

定义1[13]对每个属性子集A∈R,论域U的不可分辨关系IND(A)可定义为

IND(A)={(x,y)∈U×U|f(x,r)=f(y,r),∀r∈A。

(4)

式中,IND(A)是一个等价关系,它将论域U划分为U/IND(A)。

定义2[13]在知识表达系统S=〈U,R,V,F〉中,对每个样例子集X∈U(其中X={x1,x2,…,xn}),A是一个等价关系,X关于A的上近似和下近似的定义如下:

论域U被X的上下近似集划分为正域PA(X),负域NA(X)以及边界域BA(X)3个互不相交的区域。分别定义为

2 粗糙集图像分割

2.1 图像粗糙集

在对图像的研究和应用中,人们往往只对图像的某些部分感兴趣,通常称这些部分为前景,即目标对象,余下的部分被称为背景。在这里,将图像视为像素的集合,即论域U为一幅由像素集合组成的图像。以图1(a)所示的图像为例,白色的背景上包含一个黑色的不规则图形目标,对于单一阈值,图像二值化[14]后如图1(b)所示,目标O和背景B的粗糙集的上下近似集如图1(c)所示。

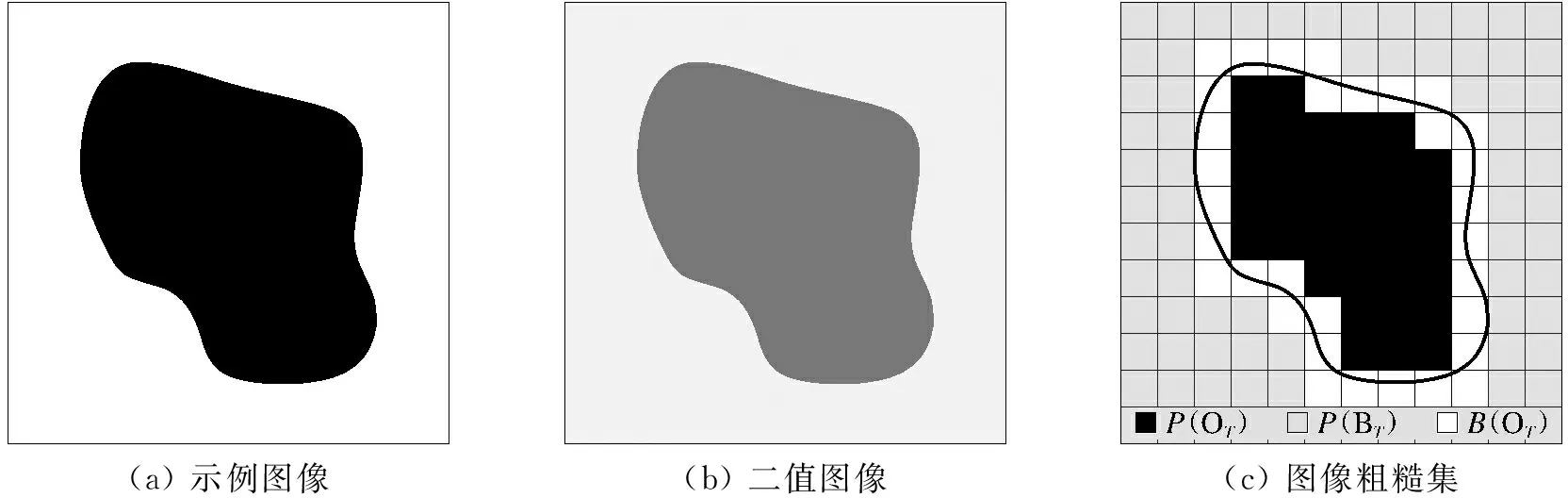
(a) 示例图像(b) 二值图像(c) 图像粗糙集

将图像分割成一个个不重叠的子块G,假定图像的目标灰度值大于背景灰度值,图像灰度级为L,即图像灰度值为{0,1,…,L-1},对于给定的灰度阈值T,背景区域和目标区域的灰度区间可以分别表示为{0,1,…,T}和{T+1,T+2,…,L-1}。论域U上的映射g:U→{0,1,…,L}是指像素P处的灰度值用g(P)表示。在这个基础上,目标和背景可看作2个集合,图像目标和背景的上下近似集表示为:

利用粗糙集的近似能力,提出了一种熵测度[15],称为粗糙熵,记为RT。通过粗糙熵来量化图像的不确定性,粗糙熵定义如下:

(14)

式中,ROT和RBT分别定义为图像的目标粗糙度和背景粗糙度。

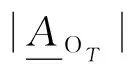
根据式(10)～式(13)的上下近似集合中图像目标和背景的关系, 图像论域U被划分成互不相交的3部分, 即正域、负域和边界域。 事实上, 任意图像的边界都具有一致性, 由图1(c)可以看出,B(OT)=B(BT), 还可以看出, 整个图像除了目标正域(下近似)和背景正域(下近似)外, 只剩下边界域的部分,即

U-P(OT)-P(BT)=B(OT)=B(BT)。

(17)

这也为本文通过粗糙集理论寻找模糊的边界提供了理论支撑。

2.2 自适应分割子块

在对图像进行分割时,每个分割子块G的大小对得到的粗糙熵的结果具有很大的影响,本文假设分割子块为h×h大小的正方形,因此如何选取h的值是一个关键问题。以往粗糙集分割图像方法需要人工指定分割大小,但在缺乏图像先验知识的情况下,即使仔细挑选,也必然会存在疑问和弊端。

局部灰度标准差(LGSD)[16]是指图像粒Gi内部所有像素灰度值的标准差,反映了图像粒Gi中灰度的对比度变化程度,灰度的对比度变化程度越高,LGSD值越大。其计算公式为

(18)

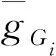
当V取得最小值时,对应的h值可作为自适应划分的最佳值。

3 本文算法

考虑到图像中目标对象之间的边界难以区分,利用粗糙集具有处理不确定性的能力,通过颗粒的计算尽可能找到实际的边界,此时粗糙集的上下近似分别对应图像颗粒的外部近似和内部近似,这使我们处理实际问题时更有意义。粗糙集的下近似的表示肯定属于目标区域的像素集合,而下近似集被上近似集所包含,2种近似值的差异为图像目标提供了一个可能的边缘区域,通过将图像颗粒化,图像中目标对象的区域得以近似化。假设颗粒大小为2×2,即每个微小颗粒中含有4个像素点,根据式(10)和式(12),可知当图像中的所有像素值都大于阈值或小于阈值时,可以认为颗粒是物体的内部近似,此时颗粒内部的大小是均匀的。否则,根据式(17),除去内部大小均匀的颗粒,余下的颗粒相连将被视作包含图像目标对象之间的边界。

表1 不同阈值个数下像素可能标记情况

单一阈值对图像二值化后只描述了一个对象,由于图像中具有多个我们感兴趣的目标对象,因此需要多个阈值对图像进行分割。比较图像中像素与每个阈值的大小,若像素值大于阈值,则像素将标记一个大写的英文字母,否则标记小写的英文字母,例如:对于第一个阈值T1,大于T1的像素将标记一个大写的英文字母A,小于T1的像素将标记小写的英文字母a,对于不同的阈值个数,像素可能存在的标记情况如表1。通过对像素的标记可将像素分类,具有相同字母标记的像素属于相同的类别。

假设(m,n)为滤波器窗口w×w内的中心位置,(i,j)在中心像素的邻域内,令新的滤波核为ρ(i,j),则新的滤波器归一化因子可表示为

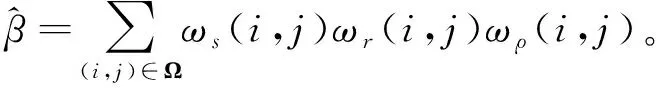
(22)

ρ的值根据滤波器窗口内中心像素点与当前像素点的关系而定。

1) 当2像素点的类别不同时,说明2像素间有边界穿过,为了降低当前像素点对中心像素点的影响,应尽量减小ρ的值,此时令ρ∈[0.1,0.3]。

2) 当2像素点的类别相同时,可分为2种情况:若当前像素点在边界处,则中心点也应在边界处,此时分配一个中等大小的ρ值给当前像素来相对保留这个边界,ρ∈[0.4,0.6];若当前像素点不在边界处,则中心像素点也不在边界处,说明此时两像素在同一个目标(背景)区域内,故应使ρ值偏大来加强两者之间的密切联系,此时ρ∈[0.7,0.9]。

图2是本文算法流程图。

首先,通过OTSU方法[17]求得多个初始阈值T。然后通过自适应图像分割子块G的大小得到最佳的分割尺寸,此时可将要处理的带噪图像划分成一个个大小相同的分割子块,对每个划分后的图像子块进行计算,将初始阈值通过粗糙集上下近似集的计算得到粗糙熵优化阈值。通过颗粒的计算将边缘像素和非边缘像素区分开来,再比较图像像素与优化阈值的大小得到像素的类别标记。最后,根据滤波器窗口内中心像素点与其邻域内像素点的关系,对新的滤波核的权重赋值得到改进的双边滤波器,用改进的滤波器对图像进行去噪,达到理想的效果。

4 结果与分析

实验在MATLAB2020A平台下完成,选取了“Lena”“Goldhill”和“Peppers”3种灰度图像进行实验,图像为BMP格式。相较于椒盐噪声等,本文算法更擅长处理高斯白噪声,通过添加不同密度的高斯噪声得到实验中的噪声图像。

4.1 算法评价指标

本文采用峰值信噪比(peak signal-to-noise ratio,PSNR)和结构相似性(structual similarity,SSIM)来客观评价算法的优劣[18-20]。PSNR公式如下:

式中:MSE表示当前图像X和参考图像Y的均方误差;H和W分别为图像的高度和宽度;n为每像素的比特效,每个像素用8位2进制表示,则n=8,每个像素的灰度级为2n-1=255,PSNR数值越大表示信噪比越高,即图像失真越小。

SSIM也是一种图像质量评价指标,公式如下:

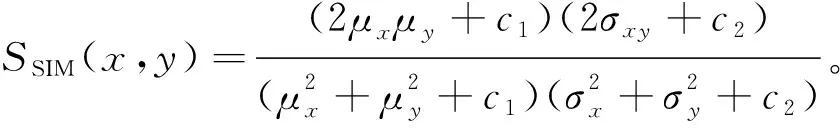
(25)

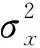
4.2 去噪结果与分析

为了验证本文算法的优越性, 以传统双边滤波、各向异性扩散算法和在双边滤波基础上发展而来的引导滤波算法作为参照, 对含有不同标准差的高斯噪声的“Lena”“Goldhill”和“Peppers”图像进行实验。 实验中各向异性扩散算法按照文献[21]设置参数; 引导滤波参数设置为γ=2,4,8;ε=0.12,0.22,0.42时的最佳指标结果。 实验结果如图3～图5所示, 表2为不同噪声标准差下的各种算法评价指标表。

(a) 原图(b) 噪声图像(c) 双边滤波(d) 各向异性扩散(e) 引导滤波(f) 本文算法

图3为“Lena”图像添加了标准差为10的高斯噪声后各算法的处理效果, 噪声强度越大, 带噪图像通过自适应子块大小得到的最佳分割子块越大, 经过计算得到的子块大小为8×8。 由于噪声标准差较小, 各算法都可以在一定程度上去除噪声, 处理后的差异并不是非常明显, 但还是可以看出,相比于其他算法的处理结果, 本文提出的算法能够更有效地去除图像噪声, 从表2中的PSNR值和SSIM值可以看出, 各向异性扩散算法与本文算法性能相似, 优于传统双边滤波和引导滤波, 但本文算法对传统双边滤波器进行了改进, 通过本文算法处理后的图像, 加强了图像纹理细节的处理, 可以保留较多的边缘特征。

图4为“Goldhill”图像的实验结果,实验中最佳分割子块大小为20×20。从实验结果对比可知,传统双边滤波滤波、各向异性扩散算法,引导滤波在处理图像的过程中,图像中房屋的细节并没有很好地体现出来。经过本文算法处理后的图像,在保留房屋纹理细节的基础上增强了图像的边缘,使图像更有层次感。

(a) 原图(b) 噪声图像(c) 双边滤波(d) 各向异性扩散(e) 引导滤波(f) 本文算法

图5为添加了标准差为30的高斯噪声后各算法的处理效果,通过自适应子块大小对含噪图像“Peppers”进行计算,得到最佳分割大小为32×32。观察实验的结果图可以发现,传统双边滤波和引导滤波的处理过度平滑了图像,前方2个物体的表面过于圆润被模糊,图像的细节特征无法完整体现,达不到理想的效果。由于噪声强度偏大,各向异性扩散算法会在一定程度上造成图像的特征模糊,不能完全滤除噪声,影响了图像的可读性,处理结果并不理想。可以看出,在噪声比较大的情况下,相比于其他算法,本文算法在有效去除噪声的同时并没有过度地平滑图像,而是保留了图像更多的细节特征。从表2同样能够看出,相比于其他3种算法,本文提出的算法在对含噪图像进行处理后,可以保持较高的峰值信噪比和结构相似性,证明了本文算法的有效性。

(a) 原图(b) 噪声图像(c) 双边滤波(d) 各向异性扩散(e) 引导滤波(f) 本文算法

通过表2各种算法的运行时间比较,可以发现,本文设计的改进滤波器需要耗费较多的时间,可见本文算法增加了时间复杂度和运算量,其实这可以从算法原理上可以得到印证:本文算法需进行阈值的优化,并通过粗糙颗粒寻找图像边界,再结合各像素点类别的判定来计算权重,并且,改进的滤波器相比于双边滤波,增加了一个新的滤波核,这注定会增加时间上的开销。比较3组图片的实验结果可以看出,本文算法通过引进粗糙集滤波核使滤波器的性能得到了提升,表2中的实验数据表明,在不同的噪声情况下,相比于其他算法,本文算法对图像的处理效果更加理想,PSNR和SSIM的值比其他3种算法更大,说明了本文算法的优越性能。

表2 不同噪声标准差下各种算法评价指标比较Table 2 Comparison of evaluation indexes of various algorithms under different noise standard deviations

5 结 论

1) 本文采用粗糙集对去噪滤波器进行改进,通过将粗糙集边界域应用于图像,通过颗粒的计算找到可能包含图像目标边界的颗粒,为滤波器提供更多边缘的信息。

2) 自适应分割子块后得到的优化阈值为下一步处理图像打下基础。

3) 实验结果显示,采用改进滤波器对含噪图像进行滤波后,图像具有最佳的指标数值。

综上所述,改进后的滤波器的性能得到了提高,能够在对噪声图像进行平滑的同时保留更多的图像细节特征,证明了去噪算法的有效性,实现了粗糙集理论在图像处理领域的应用。