卫星传输链路连通状态建模与仿真

张晨曦

（华北水利水电大学 信息工程学院，河南 郑州 450045）

0 引 言

卫星通信是通信技术、计算机技术以及航空航天技术相结合的主要产物，现如今，卫星通信已经成为有力的现代通信手段之一。卫星通信连通作为空间信息应用系统的关键环节，由于地面接收站数量和接收范围有限，卫星在轨运行期间的传输时间受到限制。

当卫星运行到不可视范围时，卫星—地面站数据传输链路无法连通，卫星星载相机采集到的有效数据无法实时传输到到地面站。目前高佳佳等人使用WorldWind 软件，仿真卫星和接收站间数据传输的动态过程，并对观测卫星过接收站的情景进行预测。Xiaobing Tang等人对卫星网络通信问题进行研究，建立了卫星与卫星之间通信网络链路可见性和连通性分析的模型。侯颖等人指出卫星与卫星之间的可见关系以及可建立星间链路的前提条件。廖希等人利用Unity 3D 建模实现了卫星通信星—地链路的三维重现和仿真运行。但对于卫星—地面站可见链路传输的建模研究暂未考虑。

本文根据卫星轨道基本特点建立了空间位置关系，通过星下点轨迹对星站位置进行几何关系判断，构建了卫星轨道空间位置和卫星—地面站连通判断的模型，对仿真实验中轨道倾角不同时的连通情况进行分析，可以协助研究人员分析或模拟卫星通信系统，具有实际和工程研究价值。

1 理论分析与建模

卫星—地面站链路连通意味着卫星—地面站在空间几何关系中相互可见，一般卫星在轨运行时，它们的可见度会不时地发生变化。要判断卫星—地面站是否连通，首先要知道卫星的位置，根据位置信息对其连通情况进行研究。

1.1 卫星空间位置模型

为了研究卫星链路的通断问题，首先必须要研究卫星的轨道特性。地球轨道卫星由六个轨道元素对卫星在空间轨道中的位置进行描述，被称为开普勒元素集。地心惯性坐标系OXYZ 下卫星轨道的示意图如图1所示。

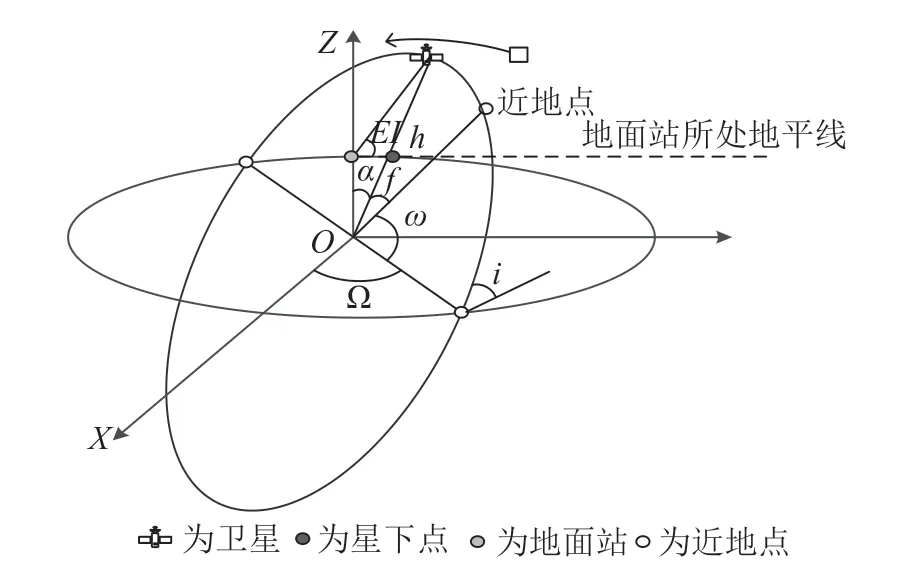
图1 地面站与卫星位置关系图

图中轨道半长轴和偏心率决定了轨道的大小和形状，轨道倾角与升交点赤经Ω 将轨道平面与地球关联起来，卫星在轨道平面的指向由近地点幅角决定，真近点角决定了卫星在轨道上的位置。假设某型号微纳卫星绕地球飞行一圈的运动轨迹为椭圆轨道，该纳卫星的飞行姿态为三轴稳定，卫星的长度、宽度和高度分别为18 cm、18 cm和22 cm，卫星质量为9.1 kg。

在对卫星整个轨道周期的连通状态进行分析建模前，需要确定卫星的实时在轨位置，通常已知卫星真近点角便可确定卫星的在轨位置。根据开普勒第二定律，可以通过确定轨道长半轴对及轨道偏心率对卫星真近点角的动态方程进行确定，计算如下：

式中为真近点角对应的卫星距地心的距离。

对于椭形轨道，取地球平均半径R为6 371 km，根据卫星距地心的距离变化可以得到卫星轨道离地面的高度，由式（3）可以得到卫星沿目标轨道的飞行周期=95.5 min。

设定卫星的初始位置，使用龙格库塔微分算法进行求解式（1）中的非线性微分方程，从而得到轨道运动仿真中卫星距地心的距离变化。

1.2 星下点轨迹建模

根据图1可知星下点为地球中心与卫星连线的交点，随着卫星的运动和地球的自转，星下点在地球表面移动连成的曲线形成了星下点轨迹。在轨道设计中，常用星下点轨迹描述卫星飞行的地面轨迹和飞经的区域，来反映卫星运动与地面的关系。

以卫星经过升交点的时间作为计算时间的零时，卫星星下点的经纬度λ与φ分别为：

式中：λ为=0 时刻的升交点经度，ω为地球自转角速度，即7.292×10rad/s；纬度幅角为近地点幅角与真近点角之和。当卫星从南向北飞时为升轨，否则为降轨。

1.3 轨道运动仿真时对数传链路通断的判断

星下点轨迹会随卫星在轨运行圈次的变化而变化，只有卫星运动到可视范围内（卫星对地面站可见），数据才可实时向地面站传输。卫星在时刻的经度和纬度计算如下。

设地面站的经纬度为（λ，φ），卫星的星下点的瞬时经纬度为（λ，φ），则星下点的瞬时经纬度与地面站的经纬度之间的夹角的计算如下。

以地面站所处的地平线为参考，由卫星轨道高度及地球平均半径R可以得到天线轴线与地面站所处地平线之间的夹角EI 为：

地面站对卫星的仰角与地面站天线最小仰角相比较，可以判断数据链路当前是否连通。若EI ＞地面站天线最小仰角，则表明当前的数传链路是连通的。

通常，地面站天线最小仰角会作为系统参数给出，受不同地形、地物以及地面噪声的影响，当仰角过低时，将不能进行有效的通信，因此国际通信卫星组织规定地面站天线最小仰角不得小于5°。

2 仿真结果及分析

根据上述模型的建立，使用计算机进行仿真，构建初始轨道仿真参数如表1所示。

表1 基本轨道参数

地面站作为卫星通信系统的重要组成部分，主要负责接收卫星向下发送的的信息，并传送给相应的地面网络用户。仿真过程中选取了部分地面站，地面站基本信息如表2所示。

表2 地面站基本信息表

为确保卫星可以经过特定的区域上方，对卫星星下点的瞬时经纬度进行计算。根据卫星轨道的建模，在地面站天线的工作仰角为5°，轨道倾角分别为60°与97°时，星下点的经纬度仿真结果以及STK 星下点经纬度的仿真结果如图2和图3所示。

图2 轨道倾角为60°时星下点经纬度仿真结果

图3 轨道倾角为97°时星下点经纬度仿真结果

经过本文仿真建模结果与STK 软件结果对比，可以看出星下点经纬度的整体趋势一致，验证了星下点模型的准确性，为后续连通性的判断奠定了基础。

在卫星运行周期内，通过数传链路连通状态判断模型的建立进行实时仿真，轨道倾角60°与97°在仿真过程中仿真圈数对应的连通地面站名称、开始连通时间、结束连通时间以及连通时长如表3和表4所示。

表3 轨道倾角60°时卫星地面站连通情况

表4 轨道倾角97°时卫星地面站连通情况

卫星沿目标轨道的飞行周期为95.5 min，设置3 个仿真周期。通过对比轨道倾角为60°与97°的连通情况，可以得到如下结论：

（1）在轨道倾角为60°时，根据卫星与各个地面站可视时间仿真的结果可知，地面站仿真3 个周期总的连通时长约为52.43 min，轨道倾角为97°时，地面站总的连通时长约为17 min。主要在于轨道倾角会影响卫星—地面站进行通信时星下点的经纬度，从而卫星过境的时间不同对应连通的地面站及连通时间不同。

（2）卫星-地面站通信时，地面站经纬度的分布不同，卫星和地面天线之间的距离不同，计算得到的数传链路的下行传输速率不同，各个地面站连通的时间不同。当卫星与各地面站同时可视时，可根据星下点与地面站位置情况，选择链路下行传输速率大或者连通地面站时间长的地面站，提升地面站接收数据的能力。

（3）根据仿真结果可知，有的地面站仿真一圈内几乎无法与卫星连通，在这时段内卫星无法进行数据传输，因此对地面站资源调度是值得进一步研究的问题。

3 结 论

数传链路连通状态是卫星进行数据传输到地面站的前提，事关卫星数据传输的使命成败。本文通过卫星空间位置对链路连通进行建模仿真，仿真结果与美国AGI 公司推出的卫星系统分析软件STK 进行对比，验证卫星星下点经纬度的准确性，能够满足卫星规划阶段对轨道精度的要求。同时对建立星地数传链路连通状态的模型进行仿真，选定了多个地面站，当卫星与地面站可见时，分析卫星地面站可视时间情况，为系统工程应用提供依据和具体方法。

卫星—地面站可以直接通过星地链路来建立通信传输渠道，当卫星与地面站不连通时，可以考虑通过中继卫星的星间链路对信息进行传输。