基于改进巴特沃斯滤波的红外图像增强算法

贾亮 邢轶博 徐善博

（沈阳航空航天大学电子信息工程学院，沈阳 辽宁 110136）

1 引言

随着红外成像技术在各个领域的广泛应用，人们对红外图像的质量也提出了更高的要求[1]。通过对图像进行增强来使其细节变得更加清晰，更有利于后期进一步的处理和使用。按照不同作用域来划分，可以在时域内或频率域中对图像进行处理[2-3]。目前，随着图像处理技术的发展，出现了针对图像增强的新算法，但是由于不同的图像性质不同，常用的传统滤波方法[2-3]都有其相对的局限性，诸如维纳滤波虽然是应用非常广泛的一种方法，但是在图像频率域上的信噪比未知的情况下不能较为准确地去噪；BM3D算法[3]是近年来较为常用的图像去噪算法，但是也存在着图像过度平滑丢失细节等问题。

针对上述问题，本文在传统巴特沃斯滤波算法[4]的基础上，用分层分别处理的方式来代替传统的只针对时域图像的单一处理方式。使用小波变换[4]对红外图像中的低频和三个方向的高频信息进行分离，分离后在频率域上使用低通滤波[7]、高通滤波[8]，以及图像增强[9-14]等方式对其进行分别处理；再通过选取适当的加权系数，对处理完的图像进行加权融合[15]；最后输出图像。经过实验验证，该方法能更有效解决传统手段处理红外图像噪声时，细节保留较差、噪声处理不明显等局限性，突出了红外图像的有用细节，提高了红外图像的空间辨识度。

2 图像分层

一般红外图像大致可以分解成基础层和细节层，在基础层中主要包含的是低频的背景信息，而在细节层中主要包含图像的高频信息。针对这种情况，可以通过一定尺度级数的小波变换将红外图像按频率的大小分解成低频部分和高频部分然后进行分布式处理。由于处理的侧重点不尽相同，所以为了能够更好地对图像进行处理，我们可以使用小波变换来对图像进行分层操作。

2.1 小波变换

小波变换是一种具有局部时域变化的函数，可以对信号在有限时间以及频率变化的情况下进行不同尺度的分析。小波变换基本原理是通过伸缩和平移基本函数来获取小波基，并使用它对输入的信号进行分解重构。通过小波变换可以将图像分解为低频部分和高频部分：

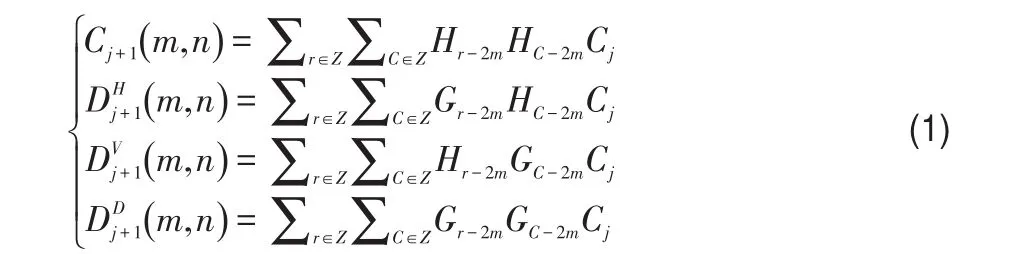
在公式(1)中Cj+1为低频信息，分别为水平方向、垂直方向及对角线上的高频信息。如图1所示，输入带噪声的原始红外图像，将其分解为低频基础图像以及3个不同方向上的高频细节层图像。从图中可以看出使用小波变换能够将图像的边缘信息和场景信息有效地分离开。

图1 分解后的高频低频图像

3 图像处理

对输入的红外图像进行分层操作后，要对低频信息和高频信息分别进行处理，低频基础层是红外图像中像素灰度值变化平缓的区域，需要对其进行去噪和增强等操作；而高频细节层是红外图像中变换较为剧烈的区域，一般包括边缘和局部纹理信息，通常一幅红外图像的噪声大部分也集中在高频部分。使用低通滤波能平滑图像噪声。但是由于图像的边缘也集中在高频部分，所以在平滑噪声的同时也会平滑图像边缘，从而造成图像不同程度上的模糊。因此，分别对红外图像的低频基础层和高频细节层进行低通滤波和高通滤波，这样可以在较好的保留边缘细节的同时去除噪声。

3.1 限制对比度自适应直方图均衡(CLAHE)

通常来说，未经处理的红外图像存在的对比度差、细节纹理不突出、灰度范围窄等问题会导致图像的整体效果过亮或者过暗，能够辨别出的图像特征相对较少。为了避免对后续的进一步处理造成不利影响，我们在对低频图像进行去噪之前，要对其灰度进行拉伸。

通过引入CLAHE算法，我们可以将低频信息的灰度值调整在一个合理的范围（图2）。该算法的主要原理是将输入图像划分成多个局部区域块，在对局部区域块进行直方图运算后，对其进行裁剪，计算裁剪幅值，即

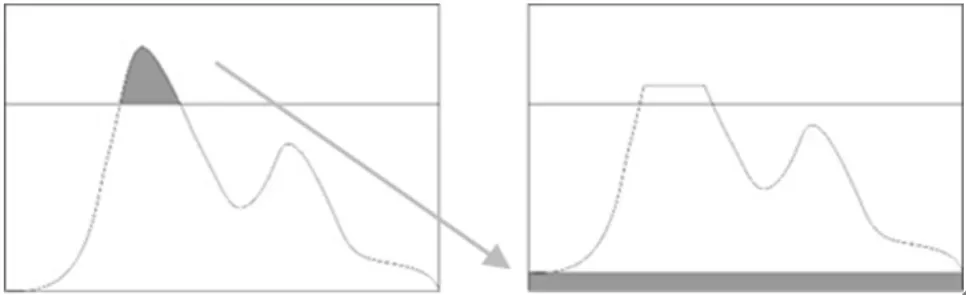
图2 像素分配原理

其中，Nclip为裁剪系数；Ux、Uy分别为x和y方向的像素个数；K为灰度级。然后将裁剪的灰度值分配到像素级上，以此在增强图像对比度和突出细节部分的同时限制噪声放大以及局部对比度的过度增强。

红外图像分离出的低频信息原图及其灰度分布直方图如图3所示，经过CLAHE算法处理后的效果以及灰度分布直方图如图4所示。

图3 原图及灰度直方图

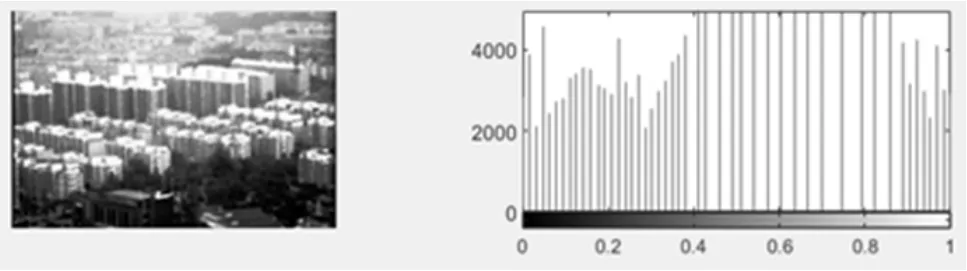
图4 经CLAHE算法处理后及灰度直方图

3.2 改进巴特沃斯滤波

巴特沃斯滤波器（Butterworth filter）是一种连续衰减的滤波器，所以也被称为最大平坦滤波器，在该滤波器不会出现太大陡峭的变化。其特点是在通频带内呈现出最大限度的平坦的频率响应曲线，没有纹波，同时在阻频带内则逐渐下降为0。其主要原理是先通过离散傅里叶变换把图像转换到频域，再进行巴特沃斯低通滤波，然后用傅里叶逆变换转换回空域，最终实现图像增强效果。其中离散傅里叶变换就是傅里叶变换在时间和频率域上均以离散的形式存在。其一维离散傅里叶变换定义为：

其中f(x)为离散序列，长度为N，u=0,1,…,N-1，则F(u)的一维离散傅里叶反变换可以定义为：

根据公式（3）和（4）可以推广出二维离散傅里叶变换，设离散函数f(x,y)，其中x=0,1,…,M-1,y=0,1,…,N-1。其定义为：

在公式（5）中，u=0,1,…,M-1，v=0,1,…,N-1。F(u,v)二维离散傅里叶反变换可以定义为：

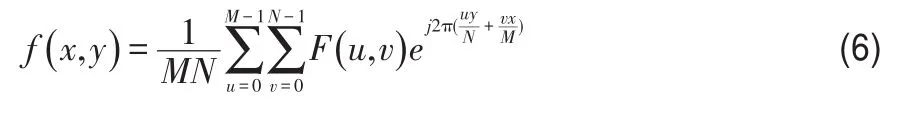
通过傅里叶变换将图像从时域转换到频域之后，就可以对其进行下一步操作，巴特沃斯低通滤波的定义如公式(7)所示：

其中D(u,v)为该点到中心点的距离，Do为截止频率，也就是振幅下降为-3分贝时的频率，Do选取的值不同其对图像的处理效果也不同。

由图5可知巴特沃斯低通滤波器在阶数相同的情况下，图像的清晰度并没有随截止频率不断增加而增强，而是先随着截止频率的增加而降低，降到一定程度后再增加。经过测试，截止频率Do在180～200之间去噪效果最好。

图5 不同截止频率下峰值信噪比的值

确定了截止频率之后，就要确定滤波器阶数n，n越大滤波器的形状越陡峭。通常取n=2，此时没有明显的振铃效应，数值更大时会有模糊效应。

在对低频分量进行处理之后，就要对高频分量进行处理，通常来说，对图像滤波降噪比较常用的是诸如高斯滤波；巴特沃斯滤波和切比雪夫滤波等基于维纳滤波器的反滤波技术。而高频图像上的一些结构边缘变化和细节，频谱系数不是那么大，往往和噪声的频谱系数差不多，甚至小于噪声的系数。这样就不能较好地对一些高频细节丰富的图像进行降噪处理，边缘会变得模糊，所以细节增强算法需要采用能够保留图像边缘信息同时去除噪声的滤波器。

改进巴特沃斯高通滤波可以在对水平、垂直、对角三个方向高频信息进行降噪处理的同时，较好地保留边缘信息。

巴特沃斯高通滤波的定义如公式(8)所示：

为了在高频率域来降噪时较好的保存边缘信息，首要工作就是要找到图像结构特征的频率带，在这些频率带上不能做过多的缩减，而在离这些频率带比较远的区域，可以增加缩减的程度。巴特沃斯响应函数在频率中心区域的半径小于D(u,v)时，函数值很接近1，变化不大；而随着距离中心点越来越远，函数值迅速减少。这一特性可以被用来进行图像降噪，考虑到要对图像进行特征的局部处理，所以定义一种改进的巴特沃斯函数：

R为进行频谱系数缩减的范围，在这个范围内，以点(a,b)为系数缩减的频率带的中心，以Da(u,v),Db(u,v)为半径的椭圆形频率带对应着图像上的条纹和细节等特征。

为了确定频谱系数缩减的范围，可以引入梯度估计的方法，在高频分量的图像中，边缘部位一般相较其他部位在频率域上有着较大的能量。点(x,y)是高频图像上某点，该点水平方向和垂直方向上的梯度分别为△x(x,y)，△y(x,y)，则可用傅立叶频谱来表示梯度：

修正巴特沃斯函数作用的范围R，一般取稍微大于梯度频谱上主要特征尺寸的固定常数，之后检测图像中的特征，即对应梯度频率中局部能量较大的区域：

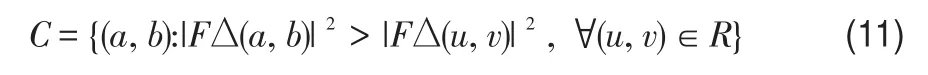
其中，C是以(a,b)为中心、半径为R的区域，设(a,b)∈C是C中的一个点，定义D1为下列集合中的最小值：

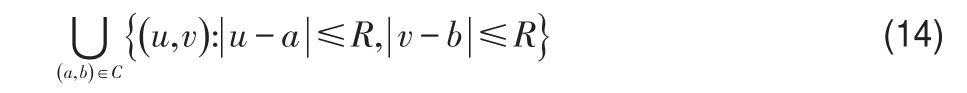
这些区域的并集给我们划定了一个图像的诸如边缘等主要特征所存在的一个频率区域，同时因为噪声频率通常覆盖了整个图像的频率域，对于在范围C之外的高频图像采用传统的巴特沃斯高通滤波，在范围内就可以使用改进的巴特沃斯高通滤波：

4 图像融合

将图像的基础层和细节层分别处理完之后，就可以按照不同比例将二者进行融合，融合公式如式(17)所示：

其中，I为经过融合后的红外图像；Id和Ih分别为低频基础层信息以及高频细节层信息；p∈(0,1)为融合参数，经过验证，当p值取0.3～0.4时最为合适，能够适应多种场景。

5 实验验证

为了验证本文改进算法的效果，通过对加噪红外图像进行处理，来对比验证算法的处理效果。实验中的红外图像，选自FLIR公开数据集，该数据集提供了带注释的热成像数据集和对应的无注释RGB图像，数据是由安装在车上的RGB相机和热成像相机获取的。

在MATLAB平台上，分别对常见的传统图像算法以及本文算法进行验证，同时使用了信息熵、峰值信噪比(PSNR)两种指标进行评价。

5.1 信息熵

信息熵是一种衡量图像内信息的丰富程度的重要指标，对于图像而言，灰度分布越广，细节更丰富，信息熵也越大。图像信息熵定义如下：

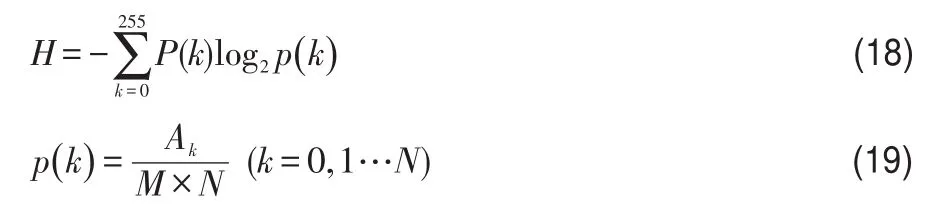
其中，p(k)表示第k个灰度级出现的概率；Ak表示第k个灰度级上的像素个数；M×N为图像大小。

5.2 PSNR

PSNR用于评价图像质量，图像峰值信噪比越大表示图像质量越好，其定义如下：

其中，m，n为图像大小；I(i,j)，K(i,j)分别为经算法处理后的图像和原始图像灰度值。算法的整体流程图如图6所示。

图6 算法整体流程图

图7为将FLIR公开数据集中选取的红外图像进行加噪处理之后，使用本文提出算法以及其余四种传统算法进行处理，由图像对比可知，本文算法相较传统算法能够显著提高红外图像的处理效果。表1为5种不同的红外增强算法在3种评价指标下得出的结果。可以看出本文提出的算法，在信噪比和细节信息的指标都相对较高，增强效果显著。

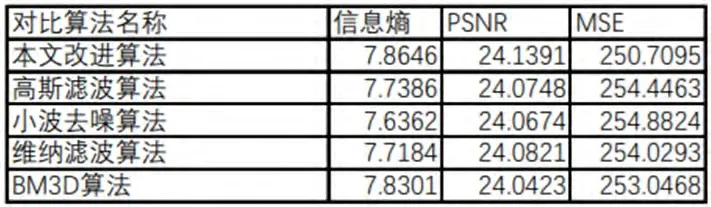
表1 不同算法客观评价结果

图7 实验结果对比

6 结语

本文提出了一种基于巴特沃斯滤波的改进红外图像去噪算法，该算法使用了分层处理的方法，将输入红外图像分解为低频基础层和高频细节层，针对低频信息使用CLAHE算法和巴特沃斯低通滤波进行处理，针对高频信息使用了改进的巴特沃斯高通滤波算法，之后再对两者进行图像融合，得到输出图像。经过试验对比验证，该算法能够较好地解决传统图像去噪算法在处理红外图像时无法较好保留边缘信息的缺点，在红外图像去噪以及细节增强方面表现较为良好。