长江中游省会城市碳足迹深度时空演变及其影响因素

胡梦姗，叶长盛，董 倩，刘 彦

东华理工大学地球科学学院，江西 南昌 330013

二氧化碳排放、全球变暖等问题严重威胁了世界各国经济及城市的可持续发展，受到社会各界的广泛关注.快速的城镇化及工业化促使能源消耗一直处于较高水平[1]，实现低碳发展是应对全球气候变暖的有效模式.制定合理有效的减排政策，需明确各区域碳排放现状与挑战.在此背景下，改变传统碳排放的量化指标，引入碳足迹深度指数并将其可视化，可直观地反映能源消耗对城市存量资本的影响程度[2]，为制定区域低碳发展的减排政策提供理论依据和决策参考.碳足迹深度是指碳生态赤字背景下吸纳1 年碳排放量理论上所需占用土地面积的倍数，代表吸纳碳排放所消耗的存量资本.碳足迹深度指数由三维碳足迹改进模型[3]计算所得，该模型通过整合碳赤字/盈余[4]，统计自然环境中资源的流量及存量，将碳足迹的广度、深度分别定义为吸纳碳排放占用的自然流量资本及存量资本.当流量资本不足以容纳年际碳排放量时，将会消耗存量资本作为补充.研究表明，武汉市、南昌市、长沙市均处于存量资本消耗阶段[5]，因此该文以碳足迹深度指数为核心进行探讨.

国内外学者对碳排放相关量化的研究主要包括以下三方面：①碳足迹的核算是国内外普遍认可的碳排放评估方法，主要有生命周期评价法[6]、IPCC 方法[7]及夜间灯光数据反演法[8]等；②碳排放影响因素包括经济发展、人口、技术、政策等，主要采用随机性环境影响评估模型[9]、拉氏指数分解模型[10]等；③对碳排放量预测提出优化方案，多运用灰色模型[11]、环境库兹涅茨曲线[12]等进行预测.就碳足迹深度的应用而言，国内学者如郑德凤等[5]研究表明，2000—2016年我国省际碳足迹深度高值区主要集中于东部沿海和中部，吸纳碳排放所占用的流量资本和存量资本存在地域互补性；曹慧博等[13]计算了我国海岸带的存量资本，发现中北部地区的存量资本消耗普遍较大，广西壮族自治区、广东省、福建省3 个省份则相对较低，且经济发展、城市规模、环境污染和区际交流是存量资本消耗的驱动因素；熊鹰等[14]在洞庭湖区以土地利用类型为切入点量化各地类的存量资本，结果表明，洞庭湖区除林地之外的其他土地利用类型均存在自然存量资本的消耗，并表现为高生态赤字.现有成果为后续研究提供了丰富的切实参考.

已有研究多从国家层面[15]或省级层面[16]展开，较少以市级尺度分析.此外，将同类型城市进行对比的相关研究尚不多见.多数学者分析了各因素对计算总量的影响，但无论是碳排放量或是碳足迹深度均是累积变化过程，单纯的线性相关会掩盖各影响因素作用的异质性，空间分位数模型能够将碳足迹深度划分为不同分位点，依次探讨各影响因素对不同分位点碳足迹深度的作用力，也可剖析各影响因素与碳足迹深度的低、中、高值间的关联性有何差异.同时，我国重点行业领域碳排放量的增长[17]会对“绿水青山就是金山银山”“‘山水林田湖草’是生命共同体”“构建人与自然和谐共生的现代化”等生态发展建设产生深远影响，因此碳足迹深度也是各行业碳排放量对生态反馈的重要表征方式.

该研究借用三维碳足迹改进模型获取长江中游省会城市的碳足迹深度指数，引入夜间灯光数据进行拟合[18]，分析比较2010—2019 年武汉市、南昌市、长沙市碳足迹深度的时空演变特征，并运用空间分位数模型深入探讨研究区不同分位点碳足迹深度各影响因素的作用水平.研究结果可为长江中游省会城市自然存量资本的耗费测算及可视化提供借鉴，同时从统计学角度实证分析碳足迹深度的影响因素，又可为长江中游省会城市碳中和目标的实现及低碳减排政策的制定提供参考依据.

1 研究区概况

在长江中游城市群中，武汉市、长沙市和南昌市3 个省会城市以“品”字型分布，是3 个都市圈的“首位城市”和“核心力量”，推动了周边区域和三省经济的高质量发展，同时也是“中部崛起”的增长极.2010—2019 年，武汉市能源消耗在研究期内达到了较高的使用水平；南昌市原煤及焦炭使用量处于增长态势，尤其焦炭使用量由117.35 ×104t 增至131.09× 104t；长沙市工业总产值不断增长，位列三市之首.在城镇建设扩张和经济快速发展的同时，土地利用结构不断变化，城市碳汇能力随之降低，因此碳排放效应对城市自然资本的掠夺性消耗，造成了十分严峻的生态压力.

2 数据来源与研究方法

2.1 数据来源及影响因素选取

能源数据、社会经济数据来源于2011—2020 年《武汉市统计年鉴》《南昌市统计年鉴》《长沙市统计年鉴》.标准煤折算系数、碳排放系数分别来源于《中国能源统计年鉴》《IPCC 国家温室气体清单指南》.林地及草地数据来源于2010—2019 年中国科学院资源环境科学与数据中心.

参考已有研究，该文选取人口密度[8]〔ln (PD)，人/km2〕、工业总产值[18]〔ln (GIOV)，万元〕、能源总量[19]〔TE，t/(104元)〕、人均碳排放(PCCE，t/人)作为碳足迹深度指数的影响因素.其中，人口密度既体现了人们对自然资源的需求，也映射了人们对生态承载力的“掠夺”.工业中的能源消耗在三大产业中占较大比重，轻工业、重工业或制造业都无法避免能源的终端消费及中间消费.能源总量是能源消耗量的直观体现，也是各类碳排放总量的数据依托.对于自然存量资本的消耗，不仅从人口、能源、工业等影响间接体现，也需要验证人均碳排放量对存量资本消耗是否存在直接影响.

2.2 研究方法

2.2.1 碳足迹深度计算

三维碳足迹改进模型[5]融合了碳盈余和碳赤字，统计了自然环境中资源的流量和存量，引入了碳足迹广度和深度(分别表示吸纳碳排放所需的流量资本和存量资本).碳足迹广度是指在碳生态承载力范围内实际占用的生态生产性土地面积，代表吸纳碳排放所占用的流量资本；碳足迹深度是指碳生态赤字背景下吸纳1 年碳排放量理论上所需占用土地面积的倍数，代表吸纳碳排放所消耗的存量资本.碳足迹广度和深度可视为圆柱体的底面和柱高(见图1)，考虑武汉市、南昌市、长沙市均处于存量资本消耗阶段[5]，因此仅探讨区域碳足迹深度的变化过程.各指标的计算公式：

式中：CEFdepth为区域碳足迹深度，反映区域存量资本的消耗程度；CEF 为能源消费的碳足迹，hm2；CEC 为能源消费的碳生态承载力，hm2；CE 为能源消费的碳排放总量，t；Qei为第i种能源的终端消费量，t；Sei为第i种能源的标准煤折算系数；Dei为第i种能源的碳排放系数，根据数据的可获取性，选取原煤(0.755 9)、焦炭(0.855 0)、燃料油(0.618 5)、汽油(0.553 8)、柴油(0.592 1)、煤油(0.571 4)、液化石油气(0.504 2)等能源；CS 为林地和草地的碳汇总量，t；Af为区域林地面积，hm2；Ag为区域草地面积，hm2；NEPf和NEPg分别为林地和草地的固碳能力，取值分别为3.809 6 和0.948 2 t/hm2[20]；Pf和Pg分别为全球林地和草地的碳汇比例，分别为82.72%和17.28%.

2.2.2 夜间灯光数据应用与处理

该研究结合DMSP_OLS V4(1992—2013 年)与VIIRS_VNL V2(2012—2020 年)原始数据，分别是第4版本DMSP 年度数据和第2 版本VIIRS 年度数据，均下载于EOG 网站(https://eogdata.mines.edu/products/vnl).将获取的DMSP 年度数据进行校正，对VIIRS 年度数据进行降噪，提取两套数据的重合年份(2012 年、2013 年)数据进行敏感度分析，选取最优拟合参数；进而根据选取的最优参数将二者合成DMSP(1992—2020 年)数据集.根据学者们总结出的共有线性、指数、多项式、对数、幂函数等5 种模型[21](见表1)，构建拟合碳估算与夜间灯光之间的函数，在此基础上选取拟合度较好的模型进行空间可视化.

表1 碳估算和夜间灯光拟合函数的模型归纳Table 1 Models of fitting function between carbon estimation and nighttime lights

经查阅，线性、多项式、对数、幂函数等形式的拟合精度更好.研究区域从县域、城市群、省域、流域等角度出发，碳相关估算值均能较好地拟合夜间灯光数据，实现空间可视化，可归纳出以下几类(见表2).

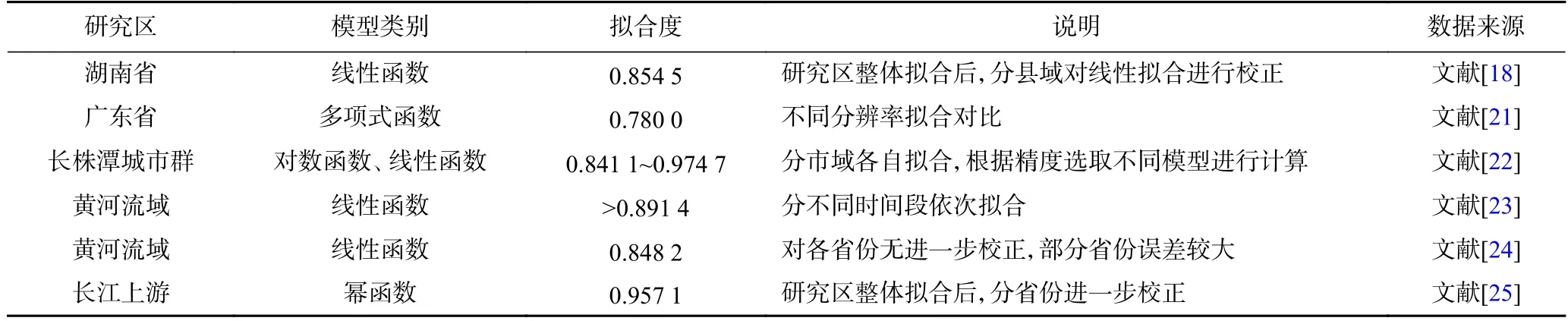
表2 国内学者应用案例归纳Table 2 Summary of domestic scholars' application cases

通过参考相关研究[18,21-25]，为使碳足迹深度指数空间可视化，同样拟合夜间灯光数据.经相关性分析发现，2010—2019 年长江中游省会城市所有区县(共310 个样本量)的实际碳足迹深度均与夜间灯光DN 值呈显著相关，拟合度为0.876 0，拟合结果在1%水平(双侧)上相关显著.初步拟合公式为

式中，y为碳足迹深度，x为夜间灯光数据的DN 值.

考虑到武汉市、南昌市、长沙市经济发展水平及资源本底存在差异，因此在参考已有研究[25]的基础上，有必要对三市的初步拟合结果依次进行修正，运用武汉市(130 个样本量)、南昌市(90 个样本量)、长沙市(90 个样本量)各自区县的碳足迹深度及相应夜间灯光DN 值依次进行拟合，通过比对线性、指数、多项式、对数、幂函数等函数结果，显示多项式函数拟合优度较高，公式分别为

式中，y1、y2、y3分别为武汉市、南昌市、长沙市的碳足迹深度，x1、x2、x3分别为武汉市、南昌市、长沙市夜间灯光数据的DN 值.通过拟合结果与实际数值比对发现，均方根误差(RMSE)为1.803 7，平均相对误差(MRE)为0.59%.因此，引入夜间灯光数据能够较好地拟合长江中游省会城市的碳足迹深度指数，通过可视化区域碳足迹深度指数，借此分析研究区存量资本消耗程度的空间分布及区域差异.

2.2.3 热点分析

Getis-Ord Gi*指数在于识别出具有统计显著性聚类的区域，反映高值要素是否能够成为具有显著统计意义的热点.利用Gi*算法对碳足迹深度的空间分布进行热点分析，设置置信度在99%以上的高值为极热团，置信度在95%～99%之间的高值区域为次热团.获取研究区碳足迹深度指数的极热团与次热团，可直观体现存量资本消耗较大区域的空间分布，将其与研究区行政区划进行匹配分析，对于存在大面积极热团与次热团的区县具有生态管控的重要警示意义.Getis-Ord Gi*指数的计算公式见文献[26].

2.2.4 空间分位数模型及指数归一化

分位数回归可以描述自变量对不同分位点因变量的影响，与普通线性最小二乘法回归相比，该模型估计值不受异常值影响，更加具有稳健性.可以不考虑同方差和正态分布假设，能够全面地反映自变量对因变量的影响趋势情况.碳足迹深度反映了区域对存量资本的“掠夺”，对生态可持续发展造成负面影响，为提出切实有效的措施建议，需要探讨研究区碳足迹深度指数增长过程中各影响因素的作用程度.该文运用空间分位数模型，分析人口密度、工业总产值、能源总量、人均碳排放量对0.1～0.9 分位点碳足迹深度的作用水平，并与线性回归结果进行对比，具体公式见文献[27].为深入剖析碳足迹深度增长累积过程中各影响因素的作用差异，有必要对区域碳足迹深度指数归一化处理，归一化公式如下：

式中，yij为第i年j地区碳足迹深度标准化后的值，xij为第i年j地区碳足迹深度实际值，maxxij为区域内碳足迹深度的最大值，minxij为区域内碳足迹深度的最小值.

3 结果与讨论

3.1 长江中游省会城市碳足迹深度时空演变

2010—2019 年，武汉市、南昌市、长沙市碳足迹深度指数均呈上升趋势(见图2)，研究结果与长江中游城市的碳压力超载状态[28]相符.2010—2019 年，武汉市归一化碳足迹深度指数由0.616 9 增至0.744 9，由主城区向外呈环状扩散，向北扩张至黄坡区及新洲区，向南蔓延至汉南区，武汉市是我国重要的工业基地，各年能源消耗量显著，区域生态系统压力较大.2010—2019 年，南昌市归一化碳足迹深度指数由0.474 0 升至0.558 2，区域归一化碳足迹深度指数以递增趋势上涨，整体分布以南昌市中心城区向四周不断扩张，并在安义县及进贤县等自然资源较为优渥的区域内呈现部分高值聚集，由于南昌市现阶段还处于化石能源为主导的能源消费结构，碳排放量与碳汇变化的不同步性加剧了碳足迹深度的增长.2010—2019 年，长沙市归一化碳足迹深度指数由0.420 8 增至0.598 4，区域碳足迹深度高值呈横向发展，由长沙市中心城区向宁乡市的北部及浏阳市的中部蔓延，碳足迹深度的剧烈增长对城市生态环境造成了不可避免的破坏.

武汉市、南昌市、长沙市各区县归一化碳足迹深度指数的变化情况见表3.结果表明，2010—2019 年武汉市各区县归一化碳足迹深度指数差异变化显著，2010 年江汉区及硚口区的归一化碳足迹深度指数高达1，发展至2019 年武汉市主城区存在6 个区域的归一化碳足迹深度指数位于高值，经董捷等[29]对武汉市各区县碳减排责任分摊的划定研究结果可知，武汉市主城区在承担着更大碳减排责任的同时也反映了其对存量资本的“掠夺”.2010—2019 年南昌市的归一化碳足迹深度高值区域为青云谱区、西湖区及东湖区，这些地区均为南昌市中心城区，区域城镇化起步较早，是早期工业园区的诞生地，并优先发展重工业，建立电力、建材等新兴工业[30]，因而碳足迹深度相对较高.2010—2019 年长沙市各区县碳足迹深度增幅有所减缓，体现了工业产业升级、能源结构优化、节能降耗持续推进的良好发展态势，其中芙蓉区、天心区及开福区归一化碳足迹深度指数较大，经过长期的建设和培育，这些地区已拥有优越的轨道交通装备产业集群[31]，在城镇化及工业化快速发展的背景下碳足迹深度指数呈现高值.

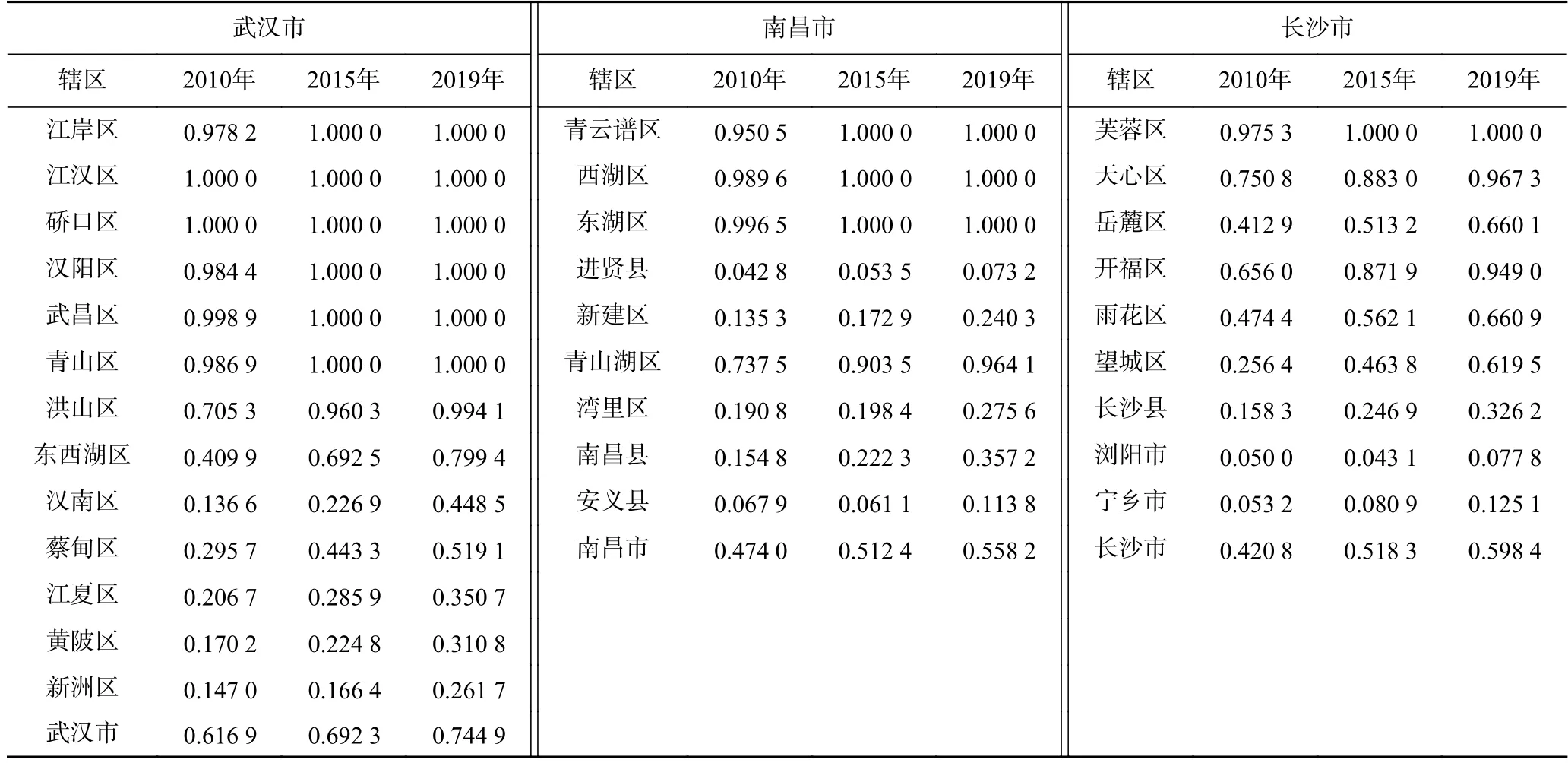
表3 武汉市、南昌市、长沙市各区县归一化碳足迹深度指数Table 3 Normalized carbon footprint depth index of each district and county in Wuhan,Nanchang and Changsha

2010 年，长江中游省会城市归一化碳足迹深度指数呈现武汉市＞南昌市＞长沙市的特征，武汉市归一化碳足迹深度指数为长沙市的1.47 倍，由于武汉市人均碳排放量比长沙市高1 t 以上，因此武汉市整体的碳足迹深度指数较高.2015 年、2019 年长江中游省会城市归一化碳足迹深度指数表现为武汉市＞长沙市＞南昌市，而长沙市在“十二五”期间通过带动大批生产性服务业发展，使二产和三产同步呼应，工业总产值再创新高，能源消耗的碳排放总量也加速涌起，自然存量资本消耗加大，碳足迹深度指数超越南昌市.

3.2 长江中游省会城市碳足迹深度空间特征

2010—2019 年，武汉市、南昌市、长沙市归一化碳足迹深度指数均在1%的显著性水平下呈现邻域分布的特征.武汉市与长沙市的正向聚集不断加强，南昌市的高值关联程度先增强后减弱(见表4).由2007 年及2012 年我国各区域各产业群的碳关联度研究可知，我国中部城市是碳关联度最大的区域，承担着我国碳减排的主要责任[32]，因此有必要获取长江中游省会城市碳足迹深度高值的位置分布(见图3).2010—2019 年，武汉市碳足迹深度极热团表现为扩张趋势，且次热团包围着极热团向四周呈地毯式蔓延，直至将武汉市主城区全面覆盖.南昌市碳足迹深度的高值于极热团集簇显著，而较高值在周边区县呈现部分聚集态势，热点团于中心城区扩张至新建区及南昌县，整体趋势向南北方向延伸.长沙市碳足迹深度极热团则以显著的“东—西”横向发展，宁乡市及浏阳市拥有丰富的碳汇能力，旅游业发展促使区域产业链逐渐完善[33]，推动了第三产业发展，使区域内呈现较小范围的极热团，在与中心城区极热团的相连区域内，次热团的衍生也体现了中心城区经济建设的发展引领.

表4 武汉市、南昌市、长沙市归一化碳足迹深度指数的全局自相关性Table 4 Autocorrelation results of normalized carbon footprint depth index in Wuhan,Nanchang and Changsha

对武汉市、南昌市、长沙市归一化碳足迹深度指数的空间趋势面进行分析，结果(见图4)表明，武汉市、南昌市、长沙市东西及南北方向均呈现“中间高、两边低”的空间分布特征.2010—2019 年，武汉市归一化碳足迹深度指数在空间分布上表现为西部高于东部、南部高于北部，且图4 中各离散点的Z轴数值不断升高.南昌市趋势线中部增长显著，而西部及南部相较于东部及北部略高，整体呈现缓慢上升趋势.长沙市归一化碳足迹深度指数在空间分布上表现为西部大于东部、南部大于北部，中心城区的Z轴高度跨度较大，归一化碳足迹指数涨幅较为明显.长江中游省会城市归一化碳足迹深度指数的整体空间分布显示，在东西方向上表现为“中间高、两边低”，而南北方向上则由“北高南低”发展为“中间低、两边高”的分布格局，且北部明显高于南部，两条趋势线均不断上升，长江中游省会城市归一化碳足迹深度指数不断增长，区域内存量资本消耗加大，长江中游省会城市生态系统正承受着巨大压力，维护生态承载力是当前的迫切问题.

3.3 碳足迹深度影响因素分析

为更好地反映长江中游省会城市碳足迹深度各影响因素的作用程度，该研究选择0.1～0.9 共9 个分位点进行回归分析.普通最小二乘法线性回归(OLS)与空间分位数回归(SQR)的拟合度(R)2均大于0.87，拟合效果较好，且各影响因素在以上两种回归结果下的相关系数存在明显差异，因此仅以线性回归反映相关性水平并不充分(见表5).空间分位数回归选用bootstrap 随机抽样，迭代400 次，获取更为精确的标准误差，分位数越大，碳足迹深度(自然存量资本消耗)数值越高.

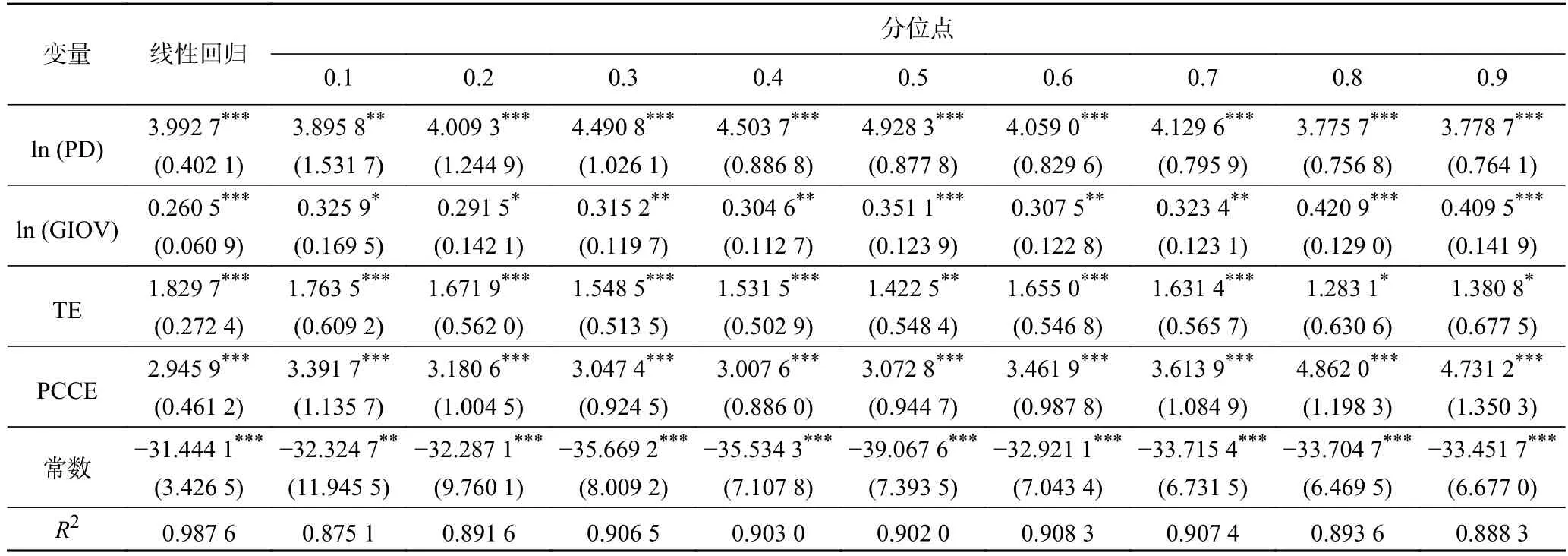
表5 空间分位数模型回归结果Table 5 Results of spatial quantile model regression

a) 对于人口密度〔ln (PD)〕，线性回归与分位数回归系数方向一致，均通过5%的显著性水平检验.在中低值区间(0.1～0.5 分位点)，人口密度对碳足迹深度的影响逐渐加强，相关系数(R)由3.895 8 增至4.928 3；而中高值区间(0.6～0.9 分位点)，随着碳足迹深度的增加，人口密度对其影响程度逐渐减弱.人口越多，对能源需求量越大，由此会显著促进碳足迹深度低值的增长；而当碳足迹深度达高值时，人口规模越大，人均资源越少，能源稀缺，将会提高城市能源利用效率[34]，减缓人口密度对碳足迹深度的促进影响.

b) 对于工业总产值〔ln (GIOV)〕，其与碳足迹深度为正向关系，均通过了10%的显著性水平.从碳足迹深度的低值(0.1～0.3 分位点)、中值(0.4～0.6 分位点)、高值(0.7～0.9 分位点)来看，随着碳足迹深度分位点的增长，工业总产值的正向影响不断加强.在各分位点中，工业总产值与0.8 分位点的碳足迹深度相关性(R=0.420 9)最强.现如今，各市工业能源消耗仍以原煤为主，且工业是碳减排经济性最高的领域[35]，因此工业产业布局的优化调整对碳减排及减缓碳足迹深度均是重要举措.

c) 对于能源总量(TE)，线性回归系数与各分位点相关系数符号同步，均位于10%的显著性水平下.能源总量对碳足迹深度中低值(0.1～0.5 分位点)的正向影响不断降低，于碳足迹深度0.6 分位点处增长后持续降至更低.在碳足迹深度0.1 分位点处，能源强度的影响最为强烈(R=1.763 5)，反映了在自然存量资本消耗初期，能源消费量的增长是存量资本耗费的重要原因，而到存量资本消耗后期，受产业结构优化调整、绿色能源使用比例上升的影响，能源总量对碳足迹深度的作用逐渐减弱.

d) 人均碳排放(PCCE)各分位点均达到1%的显著性水平，人均碳排放与碳足迹深度中低值(0.1～0.4分位点)的相关系数不断减小，对碳足迹深度中高值(0.5～0.9 分位点)的影响程度不断加剧.其中人均碳排放量对0.8 分位点碳足迹深度的影响最大(R=4.862 0)，人均碳排放量越多，对碳生态承载力造成的压力越大，进而需要更多的自然流量资本补足，而当流量资本不足以吸纳碳排放量时，对存量资本的消耗将不可避免.

该研究尚存些许不足，影响因素暂未考虑政策方面[36]，仅从人口、工业、能源消耗等角度选取，在今后的研究中将会更加完善.

4 结论

a) 2010—2019 年，武汉市、南昌市、长沙市碳足迹深度指数均呈上升趋势.2010 年，长江中游省会城市归一化碳足迹深度指数呈现武汉市＞南昌市＞长沙市的特征，2015 年及2019 年长江中游省会城市归一化碳足迹深度指数均表现为武汉市＞长沙市＞南昌市.三市的归一化碳足迹深度高值范围均以城市的中心城区向四周扩张，碳足迹深度不断增长，区域存量资本消耗严重.

b) 2010—2019 年，武汉市、南昌市、长沙市归一化碳足迹深度指数均在1%的显著性水平下呈现高值聚集的特征，极热团基本完全覆盖中心城区，次热团包围着极热团向四周蔓延.由空间趋势面分析可知，长江中游省会城市归一化碳足迹深度指数在东西方向上表现为“中间高、两边低”，而南北方向上则由“北高南低”发展为“中间低、两边高”的分布格局，且北部明显高于南部，两条趋势线均不断上升.

c) 人口密度对碳足迹深度的影响表现为先升后降，对碳足迹深度高值(0.8～0.9 分位点)的促进作用低于其余分位点；工业总产值对碳足迹深度的影响呈波动上升趋势，对存量资本高值消耗的促进作用最为显著；随着分位点的增长，能源总量的影响程度持续下降，能源总量是存量资本消耗初期的重要原因；人均碳排放对碳足迹深度的影响表现为先降后升，人均碳排放量越多，存量资本的消耗越大.

5 建议

长江中游省会城市要不断进行科技创新，提高能源利用效率，打破工业能源效率的限制空间，提升清洁能源使用比例，制定不同区域的节能减排政策.

a) 对于武汉市，能源消费过高及碳生态承载力过低是碳足迹深度较高的根本原因，工业生产普遍存在低效的生产设施和高煤炭依赖度.建议：①积极发展产业转型，将产生直接碳排放的设备装置更换为低碳乃至零碳设施，节约并循环利用化石能源，从根本上减少碳排放量；②合理优化土地利用结构，通过涵养水源、控制建设用地无序占用、设立生态保护红线等措施，有效缓解林地及草地面积的破坏及恶化，增强碳生态承载力.

b) 对于南昌市，能源利用效率不足对南昌市的碳足迹深度造成了根本的负面影响，传统的化石能源使用较为粗放，造成资源的浪费和环境污染问题日益严峻.建议：①南昌市工业园区分布较为零散，引导工业向开发区集中，产业向功能区集中，形成多循环工业体系；②为降低碳足迹深度，在减小能源消费量的同时，对符合规划、不改变途径的前提下，现有工业用地通过提高土地利用效率和增加容积率的用地，并不再增加土地价款，避免工业用地的零散分布，减少对生态用地的侵蚀.

c) 对于长沙市，依托于较好的林地面积，碳生态承载力相对充裕，但仍存在城市发展建设及工业化对碳足迹深度的影响处于难以逆转的困境.建议：①为更好地建设低碳城市，在其产业发展方面应加大力度发展绿色产业，着重投资第三产业，将低碳理念贯穿产业发展的始终；②对高产能、低能耗、高附加值的低碳产业开辟绿色通道，打造低碳技术，促进低碳空间转型发展.