基于改进差分进化算法的无人机任务规划研究

2022-10-19张荣王彬

电子制作 2022年19期

张荣，王彬

（1.武汉铁路职业技术学院，湖北武汉， 430200；2.中铁第四勘察设计院集团有限公司，湖北武汉， 430063）

0 引言

无人机在过去十年的应用越来越广泛，其技术也更加成熟。无人机在智能化战场上的出色发挥，使得无人机多任务协同的研究引起了广泛的关注。虽然多无人机协同多目标分配应用广泛，但对单无人机多任务规划的研究也尤为重要，如RQ-4、MQ-1和MQ-9等无人机的生产成本和运行维护成本高，不可能实现大规模协作[1]。单无人机多任务规划与多无人机协同多目标分配一样，都是NP难题，需要获得全局最优解。为了解决计算复杂度问题，数学算法、遗传算法(GA)[2～3]、粒子群优化算法(PSO)[4～6]、蚁群优化算法（ACO)[7]等诸多智能算法被提出并改进。近年来，差分进化（DE）算法[8～9]得到了广泛的重视和应用，尤其是在多目标分配和路径规划方面。

本文针对在复杂三维地形环境和多约束条件下，如何使无人机在任务中合理分配目标，提出了一种新的自适应差分进化算法，以解决三维环境下单无人机执行多任务的困难。在解决方案中，使用三维航次成本表达无人机和目标之间的分配关系，将动态自适应变异和交叉差分进化策略进行组合来调整在搜索算法中的平衡检测和开发从而避免陷入局部最优；同时提高了无人机任务执行的精度，适用于求解无人机大规模目标任务分配。首先，在三维环境下建立单个无人机多任务规划模型及其约束条件；其次，提出了一种基于种群迭代次数和个体适应度值的自适应进化算法来调整变异因子和交叉因子，以解决当前演化过程中存在的问题；第三，通过不同规模的仿真实验，证明了IADE算法的合理性；最后，通过与其他算法的对比实验，验证了IADE算法的优越性。

1 无人机多目标分配模型

■1.1 目标函数

无人机多任务规划是一个约束优化问题。通常，这类问题同时包含了等式约束和不等式约束[10]。根据优化理论，COP的数学描述如下：

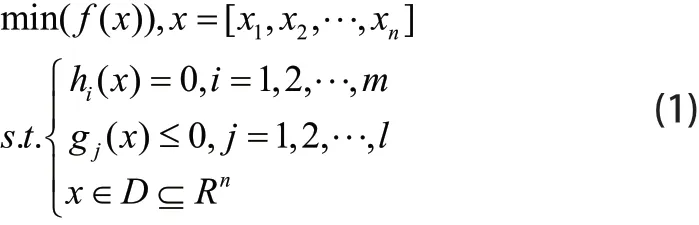
其中，x∈D表示优化问题的决策变量，f(x)为目标函数，表示待优化目标，hi(x)和g j(x)分别表示等式约束和不等式约束。

根据以上描述，结合无人机多任务分配的具体问题，可以假设单架无人机在任务空间的不同区域对多目标攻击或执行多任务。解决该问题的关键是获取攻击和执行序列，使无人机具有满足所有约束条件的最短飞行距离和最短飞行时间。

无人机多任务模型的目标函数描述如下：

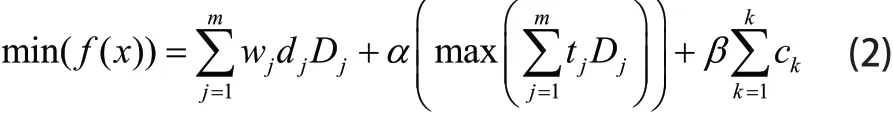
式中，dj为无人机到目标j的飞行距离，wj为j的目标权重，其取值范围为0～1，值越大优先级越高，tj为无人机到目标的飞行时间，ck为违反约束，α和β表示用于平衡目标函数多项式的比例因子，保持航次成本、飞行时间和违反约束在同一数量级，Dj表示决策变量，决定无人机的执行目标。图1显示函数的3D环境和应用场景。

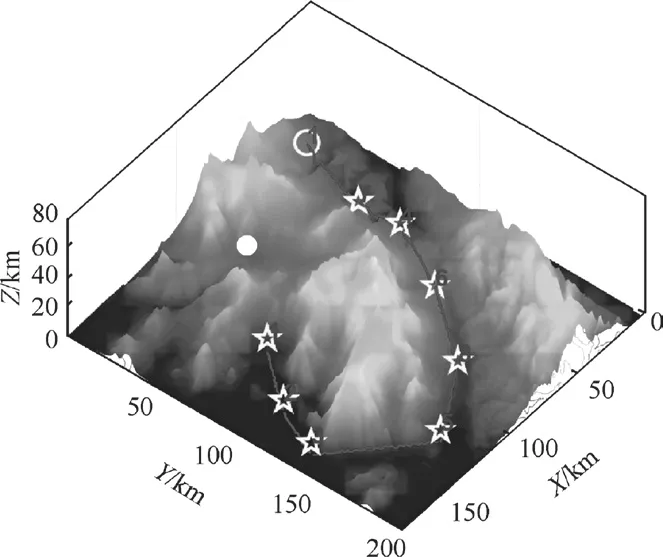
图1 三维环境的应用场景

■1.2 约束关系

（1）最大飞行距离约束

最大飞行距离约束反映无人机的性能和油耗指标，即无人机完成所有任务过程中的最大飞行距离限制。这个约束的关键是确保无人机能够完成所有的目标。约束函数表示为：

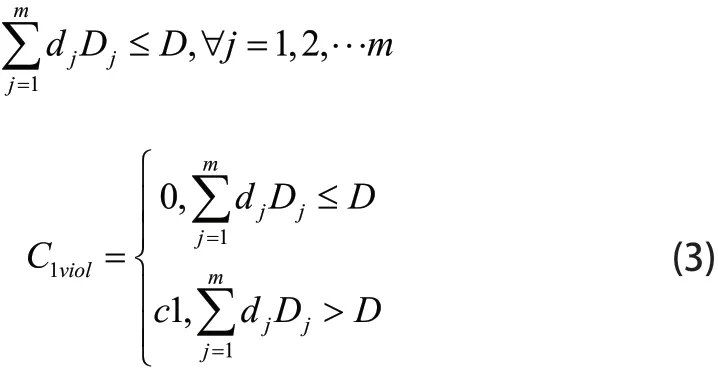
其中di为估计航程成本，D为无人机最大航程限制。C1viol表示违反约束，无人机执行第j个任务时超过最大飞行距离将受到限制。

（2）空速约束

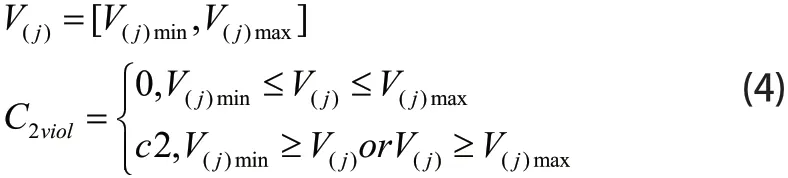
式中，V(j)max、V(j)min分别表示无人机的最大航速和最小航速；C2viol限制无人机飞行的最小和最大速度范围。

（3）最大飞行时间约束

最大飞行时间约束表示无人机完成所有任务所需的总时间。该约束的关键是确保无人机在规定的飞行时间内完成所有任务。

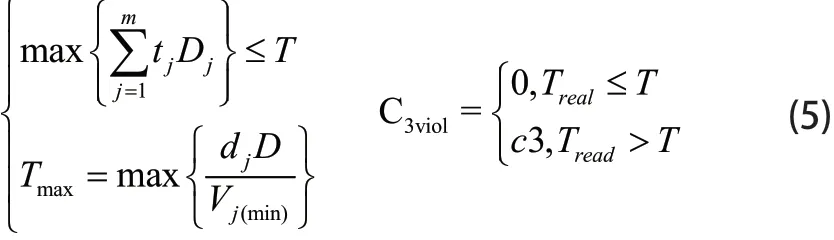
其中C3viol表示如果无人机超过最大飞行时间限制。

（4）目标点之间的时间约束

时间约束反映了目标点之间的执行顺序。重要目标点的优先级高必须优先执行，其他目标点根据约束按顺序执行。

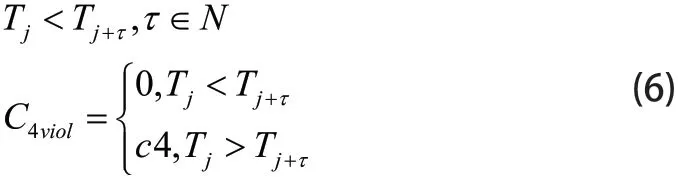
其中：Tj＜T j+τ表示目标点j必须晚于目标点j+τ执行，τ为正整数，C4viol限制目标点j后执行。

（5）最大任务数的约束

无人机执行的最大任务数由以下约束表示：

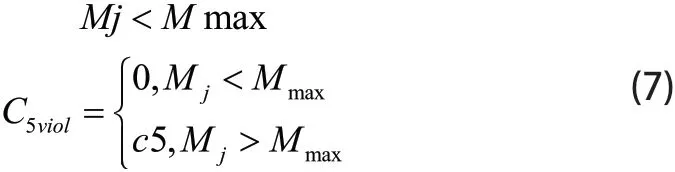
其中：Mmax表示无人机执行的任务数不超过设定执行的任务数，C5viol表示无人机任务约束。

2 改进的自适应差分进化

■2.1 标准差分进化算法

DE算法首先对种群进行初始化，然后进行变异、交叉和选择操作，不断迭代更新种群大小[11]。DE算法的步骤如下：

（1）种群初始化

DE算法在解的搜索范围的维度D内随机生成NP个体：

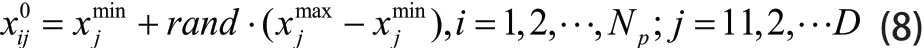
DE算法经常使用一些固定的变异策略来生成变异个体vi，以保证种群的多样性。DE算法中的确定性变异策略如下：

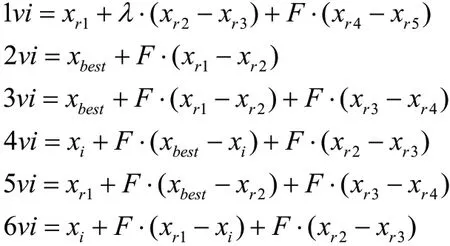
其中xbest表示最佳个体，F为比例因子，r1 r2 r3 r4 r5表示在[1,NP]上的不同随机整数，且不等于i。

（3）交叉操作

交叉运算的基本原理是将变异向量与目标向量进行参数混合，生成实验向量。具体表达式如下：

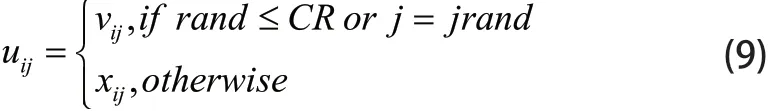
式中CR为交叉率；jrand表示在[1,D]上的一个随机整数。（4）选择操作

DE算法的主要思想是根据贪婪法则选择下一代的个体，即保留优秀的个体，剔除劣等的个体。对于优化问题，优秀个体的适应度值较小。

■2.2 JADE算法

DE/current-to-pbest作为一种新的变异策略，构成了JADE算法的基础，JADE是一种具有可选存档的自适应DE算法[12]。

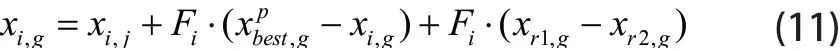
其中Fi为变异因子，与xi,g相关。的选择方法是在算法的每次迭代中，从100p%的种群中随机选择一个个体作为当前最优个体，并将其应用到变异策略中。

在JADE中，F表示为：

其中randc为柯西分布，若Fi＞1，则Fi等于1，或者重新生成Fi；若Fi≤0，初始化为0.5，更新如下：

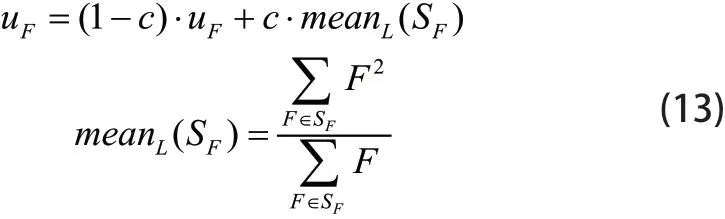
式中，c为区间(0,1)内的值，SF为所有优秀变异因子的集合。

在JADE中，CR是独立于正态分布产生的，正态分布的均值为uCR，标准差为0.1。

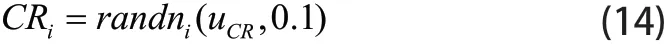
其中CiR属于[0,1]，初始化uCR为0.5，更新如下：

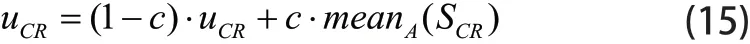
其中，meanA为平均值，S CR为所有优秀因子CRi的集合。

■2.3 PaDE算法

在整个进化过程中，PaDE算法保持k个组，并所有个体在其中进化分类。然后，uF可以根据下式更新：

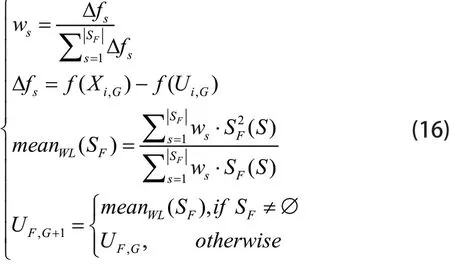
并根据以下公式更新选择概率：

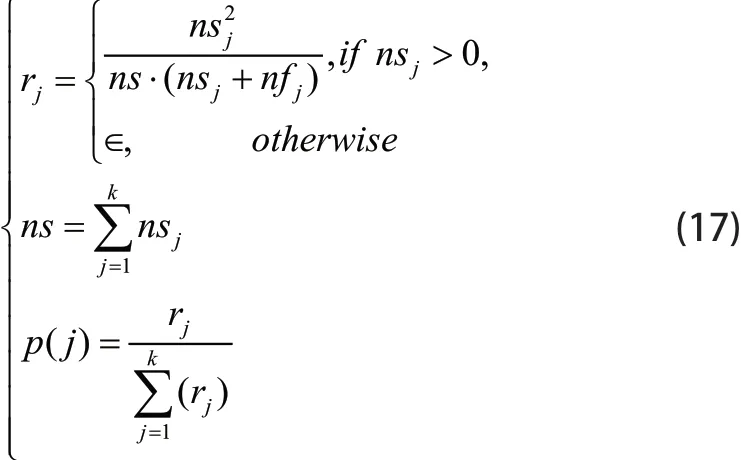
为了适应种群规模的动态变化，本文提出了一种减小抛物线种群规模的新方案。

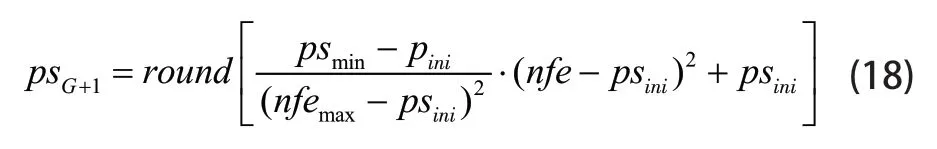
同时提出一种新的带时间戳的变异策略，可以在第一阶段初始化所有的劣等个体，然后插入到外部存档中。

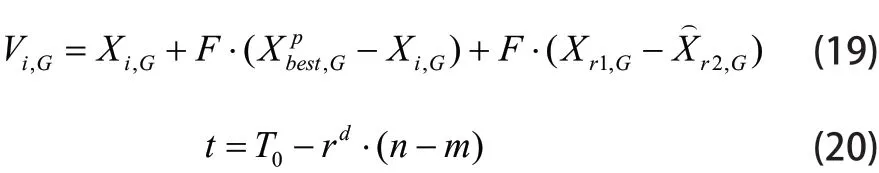
■2.4 RAM-JAPDE算法

RAM-JAPDE算法是将基于秩的变异策略自适应(RAM)和基于DE参数的联合自适应(JAPDE)相结合而产生的一种新算法[13]。RAM-JAPDE算法的主要流程及计算公式如下：

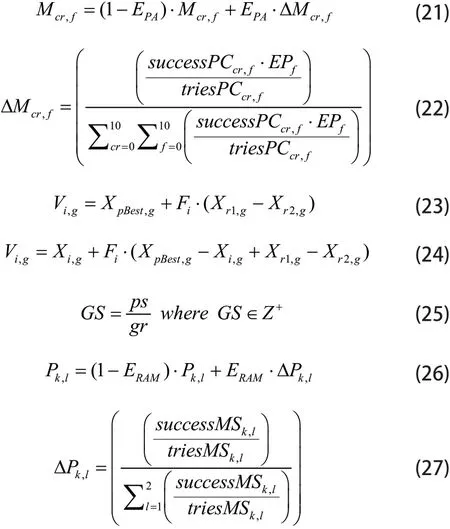
■2.5 改进机制

在众多的自适应DE算法中，变异和交叉操作是DE算法中的两个重要步骤[13]。改进主要针对F和CR，它们的值对于DE算法能否避免陷入局部最优，找到全局最优解具有重要意义。

F取值在进化的前期阶段应该尽可能大，并快速接近全局最优解，避免陷入局部最优。后期种群会聚集在全局最优解周围，因此F值应尽可能小，以提高搜索精度，找到全局最优解。CR决定了可以进入选择操作的变异个体的数量。CR值越大，可继承的信息就越少，种群更新则主要依赖于变异过程，进而丰富种群的多样性，提高了全局搜索能力。CR值较小则会缩小优化范围，但会提高收敛速度，有利于局部优化。

由于许多DE变量的F和CR值是随机生成的，不受迭代次数和个体适应度值的影响，其收敛性不如预期的好。针对这些问题，本文提出了一种改进的自适应DE算法(IADE)，同时为了使变异因子适应进化程度，提出了一种新的动态自适应变异因子。具体表达式如下：

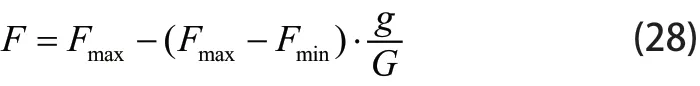
式中，g表示第g代,G为进化的总代，Fmax和Fmin分别为变异因子的最大值和最小值。

交叉因子CR控制单个参数各维度参与交叉步骤的程度，使其随个体适应度值变化，保证算法收敛的稳定性，呈现动态自适应交叉因子。具体表达式如下：

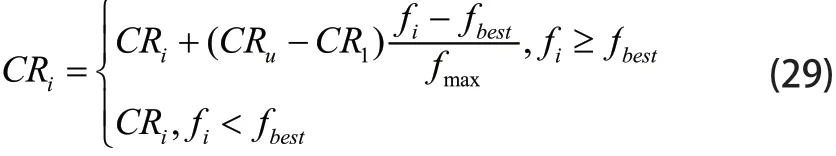
其中，CRu和CR1分别表示CR的最小和最大限制，fi为个体适应度值，fmax为最大值，fbest为最佳值。

3 实验与分析

为了验证IADE算法应用于无人机多任务规划的效果，本文进行了仿真实验，并与其他算法进行了比较。

■3.1 IADE算法的性能

为了证明算法在不陷入局部最优解的情况下找到最优解的能力的有效性，本文在不同目标数下进行了两个实验：实验1的目标尺度较小，实验2的目标尺度较大。在实验前，首先建立了三维空间地形图，并设置了无人机和目标点的初始位置，以及无人机自身的一些参数。

表1显示了初始化无人机的参数，其中Num为无人机数量，Po表示无人机的初始位置，D为无人机的飞行范围，V表示无人机的最大和最小的飞行速度，N为无人机每次飞行执行的最大任务数。

表1 无人机初始化参数

表2设置了目标点数量和位置，其中T为目标点数量。

表2 初始化目标坐标

两组实验参数设置如表3所示。其中，T为目标点，P为种群中的个体，G为进化迭代次数，Num为程序运行次数。

表3 组进化参数

图2～图3为三维环境下两组实验无人机攻击目标的最优仿真结果。黄色圆圈表示无人机的起始位置，黄色星形表示目标点的位置，红线表示无人机执行目标点任务的路径。

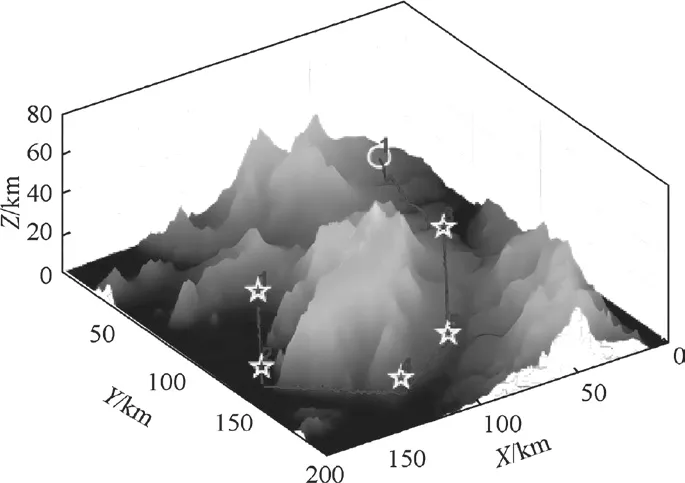
图2 实验1的仿真结果

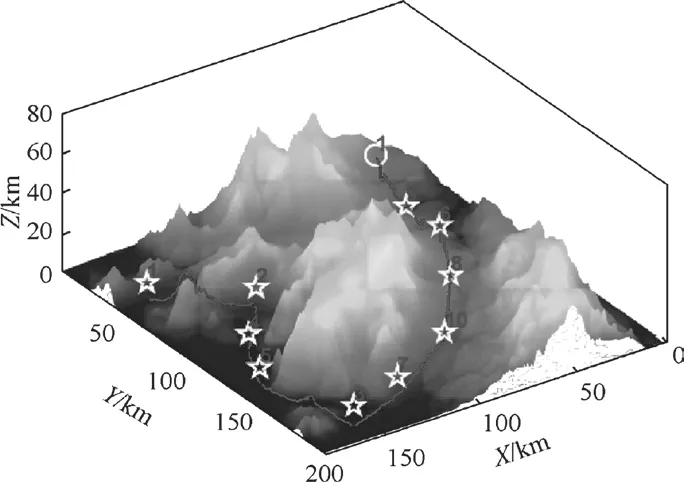
图3 实验2的仿真结果

两组实验的收敛曲线如图4～图5所示。可以看出，由于实验1中目标点数量较少，算法从进化开始到进化结束都是最优解。实验2在第50代左右收敛到最优解，说明IADE算法在进化初期具有良好的收敛性。从实验2的收敛曲线可以看出，算法执行到一半仍然收敛，这证明了在自适应变异因子和自适应交叉因子的共同作用下，算法能够有效地得到最优解。

图4 实验1的收敛曲线

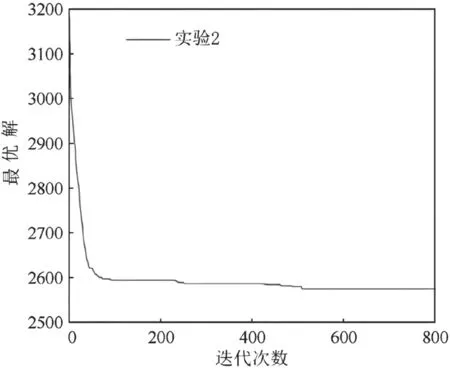
图5 实验2的收敛曲线

表4列出了两组实验结果的统计数据。其中Avgtime为算法平均执行时间，Bestcost为最优总航程成本，Avgcost为该航程的平均总航程成本，optimal为最优解比例，以百分比表示。两组实验结果表明，IADE算法能很好地解决无人机多任务问题，并能获得最优解。

表4 结果统计

通过对比两个实验的结果，虽然大规模实验2增加了无人机多任务问题的复杂性，但IADE算法仍能在有限的时间内找到最优解，最优解比例达到92.5%。实验1的规模相对较小，说明该算法能够快速得到最优解，且运行时间短，最优解比例达到97.5%。尽管实验2中的任务是实验1的两倍，但两组实验得到的最优解的平均运行时间是在同一数量级，这表明该算法适用于高效地解决不同尺度的多任务处理问题，且平均成本Avgcost接近最佳成本Bestcost。表5显示了两组实验的最优分配结果。

表5 分配结果

■3.2 IADE算法与其他算法的比较

为了进一步验证IADE算法的有效性和合理性，本文将该算法与DMDE算法和标准DE算法进行了比较。对比实验是在完全相同的仿真环境下进行的。实验结果见表6。各算法的仿真结果及收敛曲线分别如图6～图11所示。

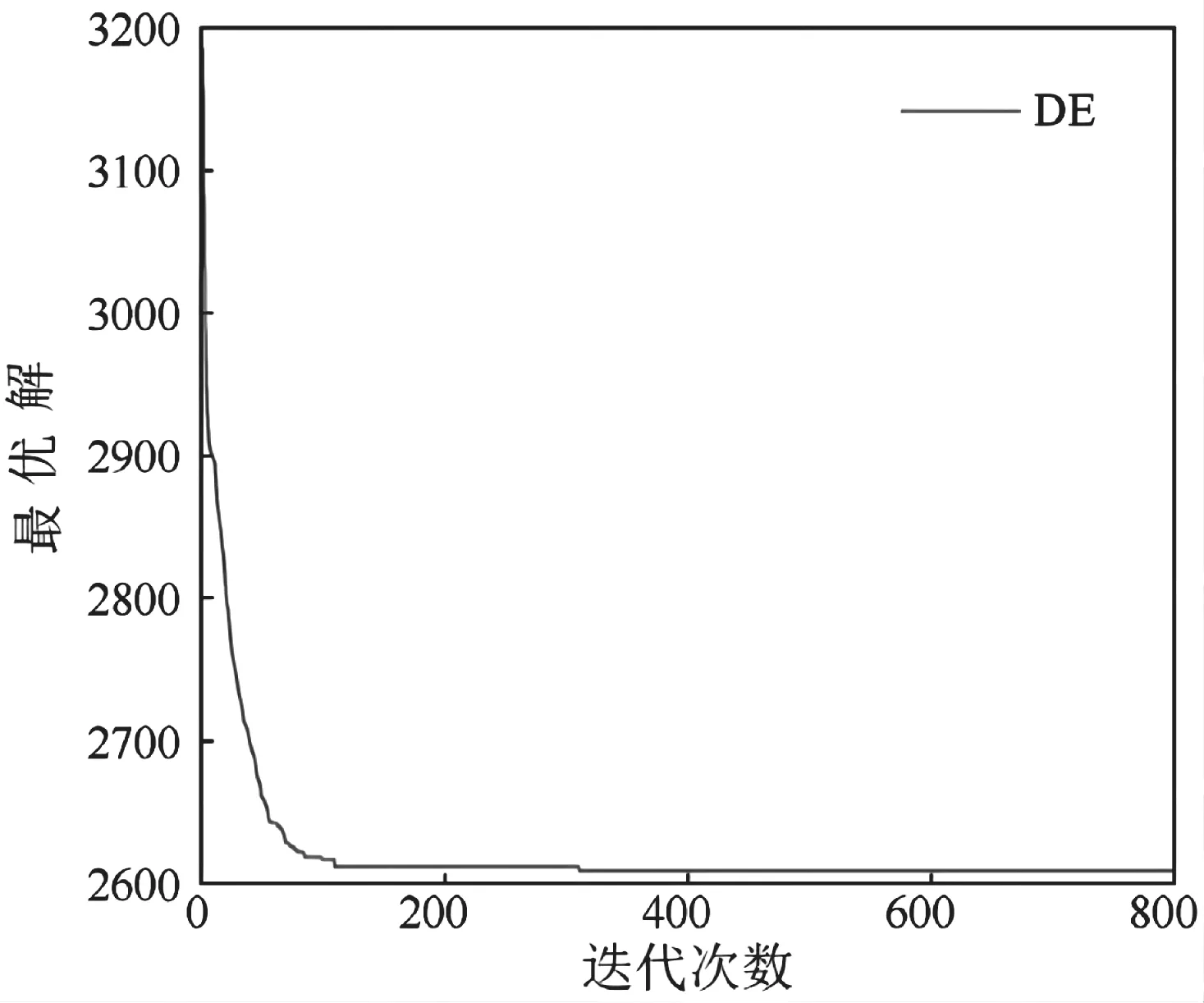
图11 DE算法的收敛曲线

表6 结果统计

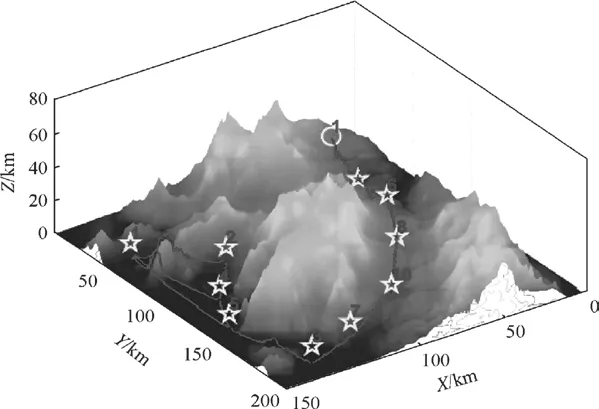
图6 IADE算法的结果

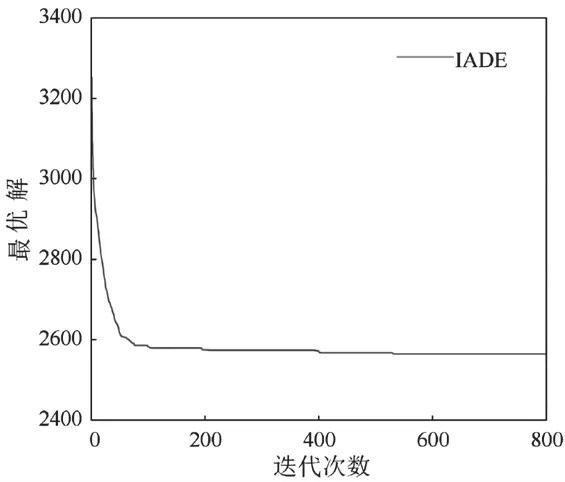
图7 IADE算法的收敛曲线

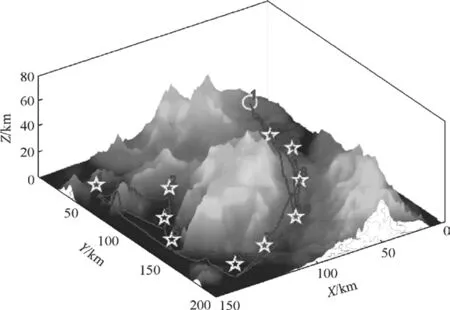
图8 DMDE算法的结果

图9 DMDE算法的收敛曲线

图10 DE算法的结果

通过对比实验可以看出，IADE算法执行时间最短，收敛速度最快，平均飞行成本最低，获得最优解的效率最高。虽然DEDM算法[14]在多无人机协同多目标分配方面表现良好，但在在任务规模较大时处理单无人机多任务时表现较差。DEDM算法运行时间最长，平均飞行成本最高，获得最优解的效率仅为30%。虽然标准DE算法优于DMDE算法，但其执行时间较IADE算法长，且得到最优解的效率为72.5%，比IADE算法低20%。