不平衡负载下独立运行双馈发电系统的矢量控制
2022-10-19张芳源景云王丹
张芳源,景云,王丹
(1.大连海事大学船舶电气工程学院,辽宁 大连 116026;2.大连海天兴业科技有限公司,辽宁 大连 116026)
近年来,新能源的利用在全世界范围内受到越来越多的关注,大力发展新能源发电技术,对于解决日益严重的能源匮乏、环境污染问题具有重大意义。双馈感应发电机(doubly-fed induction generator,DFIG)具有变换器容量低且能在不同转速下保持频率恒定的特点,使其在风力发电等领域得到广泛应用[1-3]。
独立运行是指双馈电机发出的电能直接为独立负载供电的状态。独立运行的DFIG常应用于电网未覆盖的偏远村庄、孤岛和船舶轴带发电领域[4-6]。实际上,这些负载并不总是平衡的,经常会出现瞬时负载不平衡的情况。不平衡负载将导致双馈电机发电电压不平衡,降低发电质量,而不平衡电压又进一步导致平衡负载产生不平衡电流,影响其运行性能。
为解决上述问题,文献[7-8]提出一种利用负载侧变换器消除负序定子电流来补偿定子电压负序分量的方法,然而这种方法需要提取电流的正、负序分量,导致闭环电流控制不稳定[9]。文献[9-11]采用基于双同步坐标系锁相环的电流比例积分谐振(proportional integral resonant,PIR)矢量控制方法,谐振控制器可有效控制指定频率下的交流分量,这种方法不涉及转子电流的正、负序分解,简化了控制器结构。文献[12-13]采用一种基于模型的预测电流控制方法,提高了电流控制精度,改善了暂态性能。文献[14]将比例积分重复控制方法应用于双馈电机矢量控制,利用一个控制器同时消除定子电压的不平衡和谐波分量,简化了计算过程。文献[15]提出一种不平衡负载下的直接电压控制器,该方法不需要转子电流控制器,简化了控制器结构,取得了良好的控制效果。
本文针对不平衡负载下独立运行的双馈发电系统,设计了一种基于非奇异终端滑模控制(nonsingular terminal sliding mode control,NTSMC)和改进超螺旋观测器(modified supertwisting observer,MSTO)的矢量控制方法,增强了对转子电流二倍频交流给定的跟踪性能,改善了不平衡负载条件下负序定子电压的抑制能力。这种方法不依赖于精确的电机参数,与传统控制方法相比,具有更快的动态响应和优异的稳态性能,Matlab仿真与实验结果验证了所提方法的有效性和可行性。
1 不平衡负载下DFIG数学模型
以风力发电系统为例,不平衡负载条件下独立运行的双馈发电系统框图如图1所示。风力机连接变速箱带动双馈电机转子转动,产生的电能通过DFIG定子绕组直接传递给负载;DFIG转子绕组通过两个背靠背的功率变换器连接定子绕组,包括定子侧整流器和转子侧逆变器,定子侧整流器主要用来维持电容电压稳定,转子侧逆变器为DFIG提供励磁电流,控制其独立发电运行。

图1 双馈风力发电系统框图Fig.1 Block diagram of doubly-fed wind power generation system
遵循电动机惯例,双馈电机在同步旋转坐标系下的数学模型为
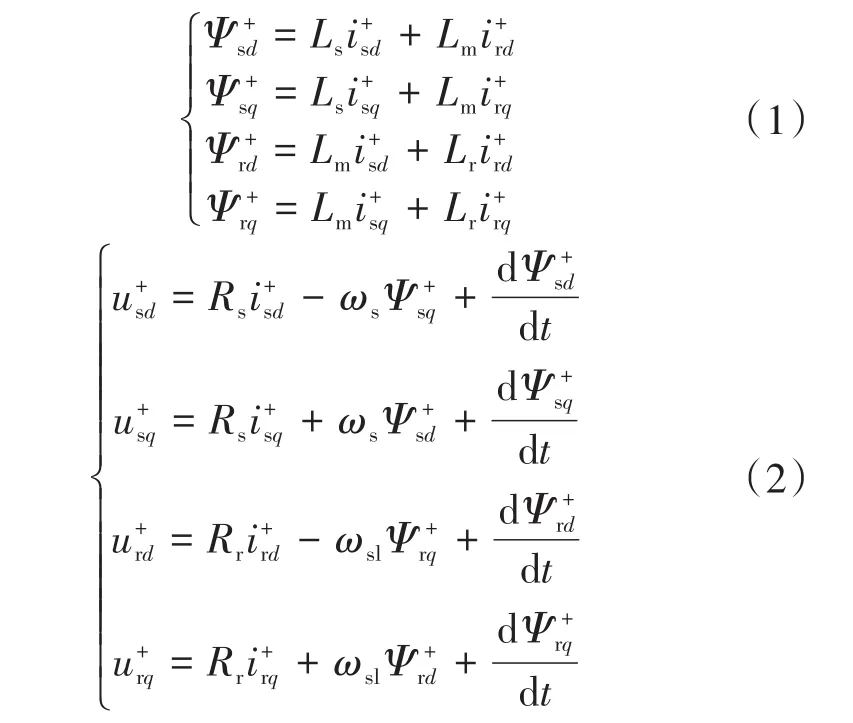
式中:u,i,Ψ分别为电压、电流和磁链;上标“+”为正同步参考系;下标d,q为同步坐标系的d,q轴;Rs,Rr分别为定子电阻和转子电阻;Ls,Lr,Lm分别为定子电感、转子电感和定转子间互感;ωs,ωsl分别为双馈电机的同步角速度和转差角速度。
独立运行的DFIG在连接不平衡负载时,会产生三相不平衡电压电流。由于三相三线制的特点,可以忽略零序电流,将电压和电流分解成正序和负序分量。在d-q坐标系中,负序分量表现为二倍频交流信号,其关系如下式所示:

式中:F代表定转子电压、电流等物理量;上标“+”,“-”分别为正、负同步参考系;下标“+”,“-”分别为正、负序分量。
正负同步旋转参考系矢量图如图2所示。由于独立运行DFIG的控制目标是定子电压平衡,所以其负序分量需要得到补偿。

图2 正负同步旋转参考系矢量图Fig.2 Vector diagram of positive and negative synchronous rotation reference system
2 控制器设计
2.1 正序分量控制
定子电压的正序分量控制采用比例积分(proportional integral,PI)控制器来实现,如图3所示,将电压幅值给定与实际值比较后送入PI控制器,来获得d轴转子电流的正序参考分量。该控制回路的目的为建立三相定子电压,同时抑制由转子速度或负载变化影响导致的定子电压幅值变化。定子电压幅值的大小由电压信号的正序分量获得,即


图3 电压正序分量控制器Fig.3 Controller of voltage positive sequence component
在定子磁链按d轴定向的前提下,忽略定子电阻的影响,结合式(1)、式(2)可以得到q轴转子电流正序参考值为

2.2 负序分量控制
为了补偿双馈电机定子的不平衡电压,使用陷波滤波器来提取负同步参考坐标系下定子电压的负序分量,并用PI控制器使其收敛到零,控制框图如图4所示。

图4 电压负序分量控制器Fig.4 Controller of voltage negative sequence component
图4中,ω0为陷波滤波器的中心频率;G0为陷波器的通带增益;ξ为陷波系数,通常取0.707。由陷波滤波器提取出的定子电压负序分量,通过参考值设置为0的比例积分控制器来获得转子电流的负序参考i-*rdq-,转子电流负序分量在负同步参考坐标系为直流分量,经坐标变换转换至正同步参考坐标系。通过电压外环的正负序控制,得到补偿不平衡电压后的转子电流总参考值如下式所示:

转子电流总参考值为直流和交流分量的总和,转子电流通过跟踪此参考值,来消除定子电压中的负序分量。但传统的控制方法(例如PI控制)无法有效跟踪交流给定,因此,需要对转子电流控制器进行改进,增强其对转子电流二倍频给定的跟踪性能。
2.3 改进转子电流控制器设计
遵循定子磁链按d轴定向的原则,结合式(1)、式(2),可得转子电流在同步旋转参考系下的一阶微分方程为

式中:λd,λq分别为系统未建模动态和外界未知扰动的影响;fd1,fq1为转子电流导数中的基频分量;fd2,fq2为不平衡负载在转子电流导数中引入的二倍频分量。
由式(7)可知,DFIG转子电流可以由转子电压控制。由于滑模控制相对于传统的比例积分控制器,具有受数学模型偏差影响小、收敛速度快、跟踪性能好等特点,采用非奇异终端滑模设计转子电流控制器。设计转子电流的非奇异滑模面为


式中:α,β为滑模面参数,且满足α,β> 0;p/q为xdβ,xqβ的指数,p,q为正奇数且满足 1<p/q< 2;xdα,xdβ,xqα,xqβ为滑模状态变量。
当系统到达稳态时,满足滑模变量及其导数收敛到0,即

结合式(7)与式(11),得到转子电流的滑模控制率为

式中:kd,kq为开关控制项系数。
滑模控制率中,开关控制部分用来补偿系统未建模动态和外界未知扰动的影响。等效控制项fd1,fq1用来跟踪转子电流给定中的基频分量;fd2,fq2用来跟踪转子电流给定中的二倍频分量,在消除负序电压分量中起了非常重要的作用。为了消除滑模控制中的抖振,用饱和函数sa(ts)来代替开关函数作为控制函数的切换控制部分。
由式(8)、式(9)可知,转子电流导数中的基频分量fd1,fq1和二倍频分量fd2,fq2的计算需要电机电感参数,会受到电机参数测量误差的影响,并且fd2,fq2的计算需要提取转子电压、电流的二倍频分量,使控制器设计更为复杂。针对以上不足,设计了一种改进超螺旋观测器,同时观测fd1,fq1,fd2,fq2的值,以d轴为例,设计的MSTO如下式所示:

式中:z1,z2,yd为观测器状态量,分别用来观测转子电流、基频分量和扰动分量(fd1+λd)及二倍频分量fd2;l1,l2,km为基频以及二倍频分量观测系数;b为参数增益,且满足b=(1/σ)Lr;e为观测器观测误差,作为z1和z2的观测稳定条件。
由于fd2在消除负序分量中起着关键作用,当系统到达滑模面并稳定时,呈二倍频正弦交流形式,所以用0-sd作为其观测稳定条件。
将MSTO观测的状态量替换式(13)中的对应量,可得MSTO-based NTSMC的转子电流控制律(以d轴为例)为

设计的d轴转子电流控制器的结构如图5所示(q轴结构相似)。
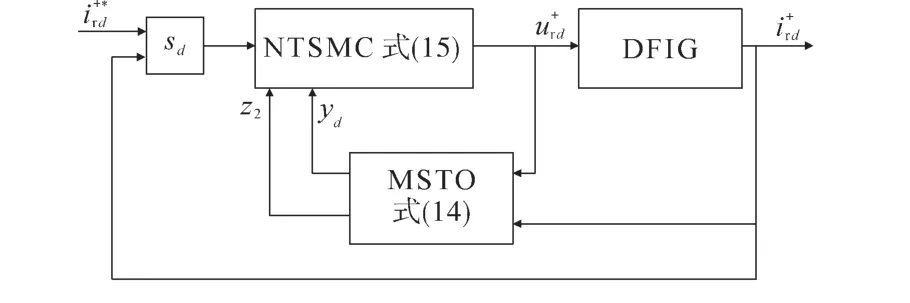
图5 MSTO-based NTSMC转子电流控制器结构框图Fig.5 Block diagram of MSTO-based NTSMC rotor current controller

2.4 稳定性证明

3 仿真验证
为了验证所提方法的有效性,利用Matlab软件中的Simulink仿真工具对系统进行仿真,仿真系统框图如图6所示。电压控制器与转子电流控制器分别应用于不平衡负载下独立运行的双馈发电系统的内外环控制器中,分别采样定子电压、定子电流、转子电流和转子位置信号,经内外环控制器后,产生SVPWM信号送给转子侧逆变器,以控制双馈发电机的独立运行。
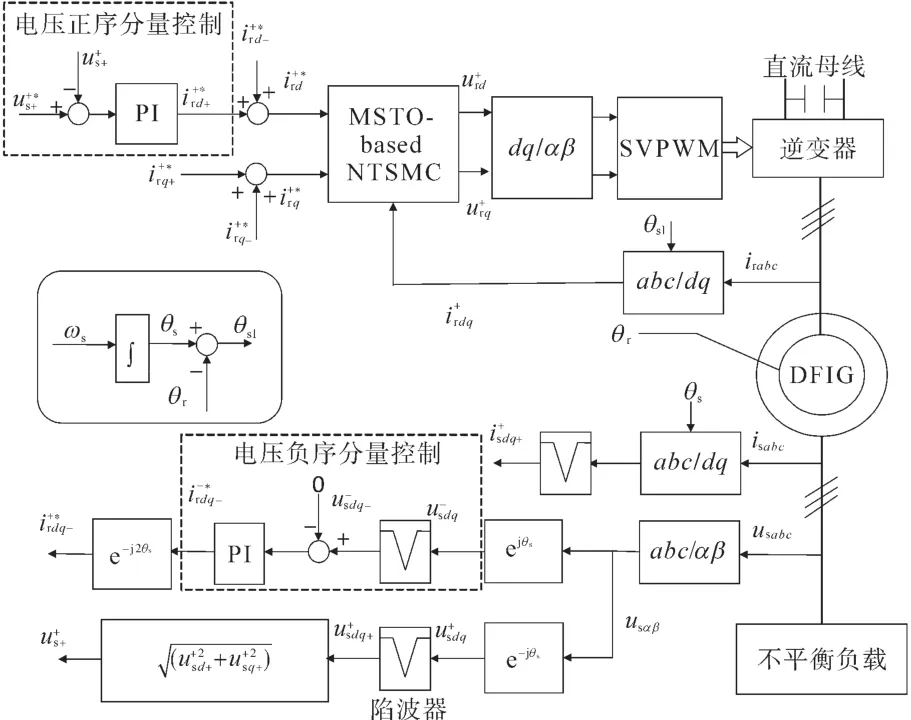
图6 不平衡负载下DFIG控制框图Fig.6 Control scheme of DFIG under unbalanced loads
本系统仿真参数的设置为:直流母线电压给定值460 V,定子电压幅值给定值155 V,角频率给定值ω*=100π rad/s;双馈电机的参数为:额定功率PN=6 kW,电机极对数2,定子电阻Rs=1.37 Ω,定子电感Ls=0.162 5 H,定转子间互感Lm=0.159 2 H,转子电阻Rr=1.65 Ω,转子电感Lr=0.163 5 H,定转子匝数比Ns/Nr=2.398。
为了验证所提算法在不平衡负载下的有效性,将本文提出的MSTO-based NTSMC控制方法,与NTSMC控制方法和PIR控制方法,在连接不平衡负载的条件下进行仿真对比。在t=0.2 s之前,DFIG定子绕组连接三相平衡负载(200 Ω,200 Ω,200 Ω);在t=0.2 s之后,切换为三相不平衡负载(50 Ω,100 Ω,200 Ω)进行测试。
本文所提方法是对转子电流控制器的改进,增强对二倍频交流信号的跟踪性能,进而改善对定子电压负序分量的抑制能力,因此对比了NTSMC控制、PIR控制和本文所提控制方法在三相不平衡负载下的q轴转子电流跟踪效果。如图7a所示,采用NTSMC控制方式时,q轴转子电流信号无法有效跟踪交流给定。如图7b所示,采用PIR控制方式时,负载变化时转子电流信号波动较大,但仍能在0.07 s之内跟踪上给定电流。如图7c所示,采用本文所提方法时,当负载变为不平衡时,转子电流的波动明显变小,过渡更加平滑,在0.04 s之内,转子电流能够迅速跟踪上给定,相对于PIR控制方法,具有更好的动态性能。

图7 不平衡负载下q轴转子电流跟踪效果Fig.7 Tracking effect of q axis rotor current under unbalanced loads
图8为不同控制方法在三相不平衡负载下定子电压幅值和电压负序分量的仿真结果。如图8a所示,在无负序抑制能力的NTSMC控制下,定子电压幅值中存在大小为22 V的二倍频波动,定子电压负序分量为usd-=3 V,usq-=20 V,电压不平衡度为5.4%。如图8b所示,采用PIR控制方式时,电压幅值波动从22 V减少为2.2 V,定子电压负序分量也削减为usd-=0.1 V,usq-=0.8 V,电压不平衡度为1.1%。如图8c所示,采用本文所提方法时,电压幅值波动得到明显改善,在0.04 s之内,定子电压负序分量被迅速削减到0。

图8 不平衡负载下电压幅值和负序分量Fig.8 Voltage amplitude and negative sequence component under unbalanced loads
为了验证所提算法在电机转速变化时的有效性,在0.4 s—0.6 s之间,将双馈电机转速从1 380 r/min逐渐上升至1 620 r/min,在三相不平衡负载下,得到的仿真波形如图9所示。其定子电流由于三相不平衡负载影响,呈不平衡状态,幅值分别为1 A,1.75 A和2.1 A,不平衡度为37.1%。定子电压在不平衡负载与转速变化双重条件下,仍为三相平衡波形,且幅值和频率仍保持不变。

图9 不平衡负载下转速变化时的仿真结果Fig.9 Simulation results when the speed changes under unbalanced loads
根据仿真结果总结可知,本文所设计的MSTO-based NTSMC转子电流控制器,相对于NTSMC控制器而言,具有良好的转子电流二倍频跟踪能力与负序电压抑制能力;相对于PIR控制器而言,在不平衡负载变化时过渡更为平滑,能够迅速跟踪给定信号,具有更好的动态性能。同时,验证了本文所提控制方法在转速变化条件下的有效性。
4 实验验证
为了进一步验证所提算法的有效性,搭建了硬件实验平台,如图10所示,并基于数字信号处理器DSP TMS320F28335编写了控制算法。采用一台功率为7.5 kW的异步电机作为原动机,异步电机与双馈发电机同轴相连,通过变频器来模拟不同转速下的DFIG运行状态。DFIG的实验参数与仿真参数相同,DSP的时钟频率设置为120 MHz。PWM的采样频率和开关频率设置为10 kHz。双馈发电机的转子电流由基于智能功率模块(IPM)PM75RL1A120的功率逆变器控制。实验数据通过CAN网以1 Mbps的速率上传到上位机,以便于状态量的观测与分析。

图10 双馈独立发电系统实验平台Fig.10 Experimental platform of stand-alone DFIG system
与仿真情形类似,在0.2 s时,DFIG定子连接的三相平衡负载(200 Ω,200 Ω,200 Ω)突变为三相不平衡负载(50 Ω,100 Ω,200 Ω),对比三种控制方法下的转子电流跟踪效果和定子电压波形分别如图11、图12所示。

图11 不平衡负载下转子电流跟踪的实验波形Fig.11 Experimental tracking effect of rotor current under unbalanced loads
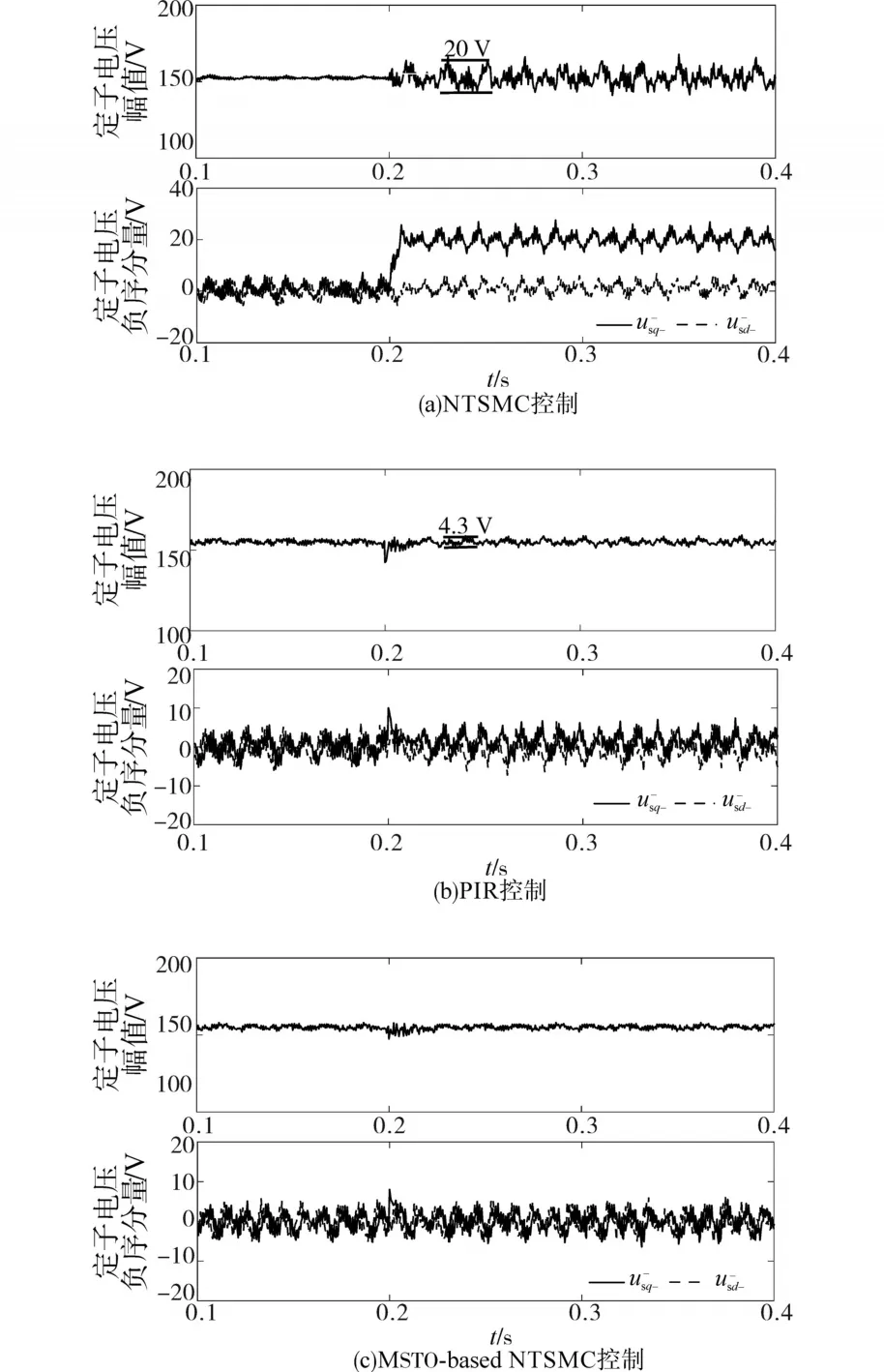
图12 不平衡负载下电压幅值和负序分量的实验波形Fig.12 Experimental waveforms of voltage amplitude and negative sequence component under unbalanced loads
以q轴转子电流为例,如图11a所示,在负载不平衡情况下,采用NTSMC控制方式,无法实现转子电流对交流给定信号的有效跟踪。对比图11b和图11c可得,PIR控制方式的调节时间是0.06 s,而MSTO-based NTSMC的调节时间是0.025 s,本文所提方法的动态响应速度要优于PIR控制,具有动态性能优异的特点。
由图12可得,在采用NTSMC控制方式时,定子电压负序分量为usd-=2 V,usq-=21 V,定子电压幅值存在大小为20 V的二倍频波动,电压不平衡度为5.1%;采用PIR控制方式时,定子电压负序分量为usd-=0.5 V,usq-=2.3 V,电压幅值波动减少为4.3 V,电压不平衡度为1.3%;采用本文所提MSTO-based NTSMC控制方法时,定子电压负序分量被削减到0,电压幅值的二倍频波动也得到有效抑制,说明本文所提方法在不平衡负载条件下的负序电压消除能力更优。
在连接三相不平衡负载条件下,采用所提算法在电机转速变化时的实验波形如图13所示,在3 s—4 s时,双馈电机转速从1 380 r/min线性上升至1 620 r/min,转子电流频率由4 Hz缓慢变为零后反相,之后再次上升至4 Hz。同时,为了保证定子电压的平衡,转子电流中引入了二倍频交流分量。进一步分析3 s—3.5 s期间的定子电压和电流波形可知,当转速发生变化时,定子电压仍为三相平衡波形,且幅值和频率保持不变,具有变速恒频的特性。定子电流的波形稳定,不受电机转速变化的影响,其幅值分别为1.1 A,1.81 A和2.2 A。实验结果表明,本文所提算法在转速变化时也具有优良的负序电压抑制性能。
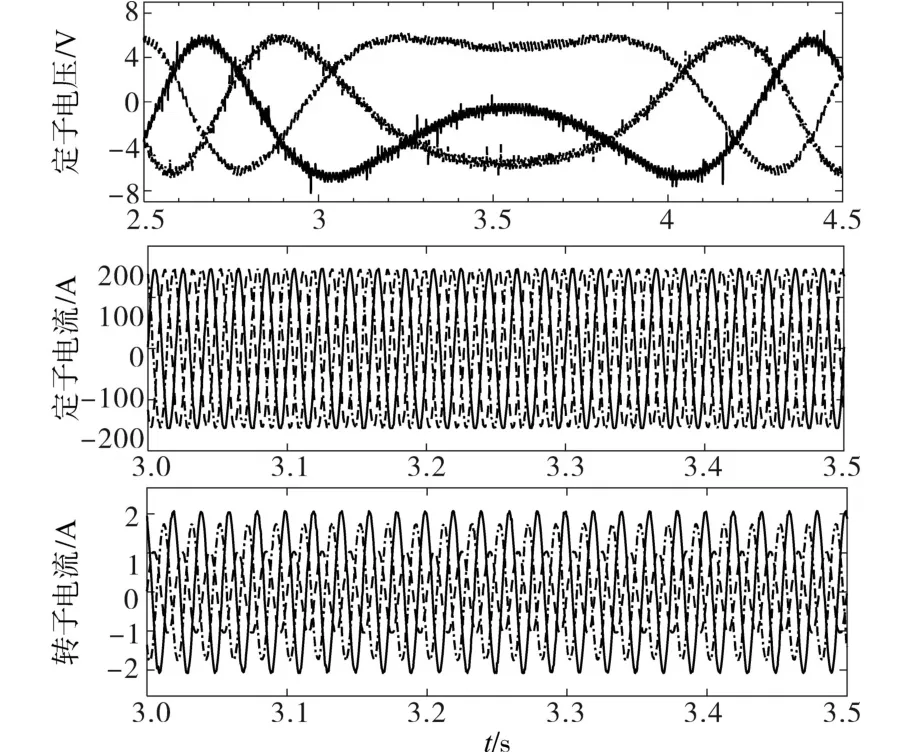
图13 不平衡负载下转速变化时的实验结果Fig.13 Experimental results when the speed changes under unbalanced loads
5 结论
本文针对不平衡负载下独立运行的双馈电机控制,提出了一种基于改进超螺旋观测器和非奇异终端滑模的矢量控制方法。通过MSTO同时观测转子电流的基频和二倍频分量,提升了系统的抗干扰能力。将MSTO-based NTSMC应用于转子电流控制,使控制器能够快速有效地跟踪转子电流二倍频给定信号,改善了对定子电压负序分量的抑制能力。所提方法与传统方法相比,减少了对电机参数的依赖,提升了系统的鲁棒性。仿真与实验结果表明,这种方法具有快速的动态响应和优异的稳态性能。
