基于重叠区域位置估计的图像拼接

秦禹杰 孙先松 李轩

摘要：针对图像拼接中特征点提取和匹配耗时长的问题，提出了一种重叠区域位置估计的图像拼接方法。首先输入图像对并进行预处理，得到二值梯度图;其次两幅图像水平向滑动，记录每次重合的区域;然后将水平向重合区域纵向滑动，计算每次重合时的方差，并取最小值作为水平向重合区域的相似度;最后在配准阶段只对相似度值最小的水平向重合区域进行特征点提取和匹配，并利用随机抽样一致（RANSAC） 算法进行单应性矩阵计算和鲁棒校验。实验结果表明，该方法不仅有助于估计图像对的重叠区域位置，而且匹配对和特征点的比值提升了0.2～5倍，显著提高了图像配准的效率。

关键词： 图像拼接; 重叠区域位置估计; 图像配准; 随机抽样一致; 鲁棒校验

中图分类号：TP391        文献标识码：A

文章编号：1009-3044（2022）25-0015-05

开放科学（资源服务） 标识码（OSID） ：

1 概述

因为相机拍摄视角的局限性，单幅图像的视野相比于人类双目视觉的视野要小，因此在需要获得大视野图像时，就得使用图像拼接技术對两幅或多幅图像进行拼接。图像拼接技术在许多领域有着应用，如全景视频[1]、虚拟现实[2]和矿物分析[3]等。

图像拼接技术主要有两个步骤，分别是图像配准和图像融合，其中图像配准是关键，直接决定了图像拼接的效率和质量。图像配准又由特征提取、特征匹配、单应性矩阵计算和图像插值与变换组成，其中特征提取和特征匹配最为耗时，一般来说至少占整个拼接计算时间的60%。特征提取算法用于获取图像的特征信息，如Harris[4]、SIFT[5]、SURF[6]等。特征匹配算法的目的是通过特征描述符距离计算找到匹配对，从而确定重叠区域的位置和图像变换的参考图像，但当非重叠区域的无效特征点较多时，不仅会降低图像配准的效率，而且会影响单应性矩阵的质量，特别是在进行大批量图像拼接的时候。

为了更有效率地获得优质匹配对，找到重叠区域，研究人员在图像配准方面做了一些工作。针对特征点提取效率问题，Qu等人[7]提出了一种基于二值子图像像素个数和方差相似度的重叠区域位置估计算法，使特征点的提取更有针对性，优点在于大量无序图像拼接时能减少较多计算时间，但没有给出估计错误的解决方案和提及准确率的问题。针对特征点匹配效率问题，Qin等人[8]提出了一种基于分割子图像和压缩的匹配算法，使用压缩了高度的10个子图像分别进行特征点匹配，优点在于可以有效利用计算平台的硬件优势，并获得更多匹配对，但子图像只包含了部分原图像的特征信息，较容易产生错误匹配对，降低了单应性矩阵的质量。

本文的主要思想是采用图像处理的方式对重叠区域位置进行估计，减少无效特征点提取和匹配的计算时间，从而提高图像配准的效率，它的优点是可以分块并行计算，且实现起来较为容易。

2 图像拼接算法

2.1 本文算法流程

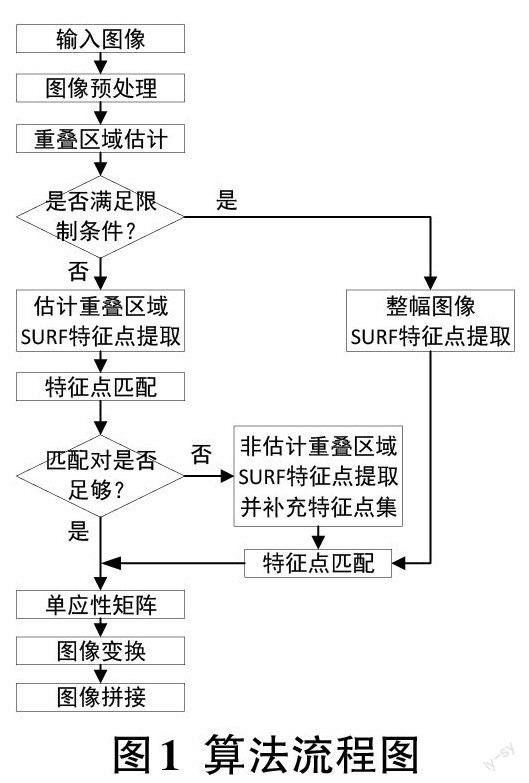
本文的图像预处理和估计限制条件是保障估计准确率的关键，图像预处理可以为后面的步骤提供有大量特征信息的图像，估计限制条件可以有效防止时间消耗，两者共同保证了本算法的可靠性，在此基础上计算水平和垂直方向滑动重合时的方差，并对估计出的重叠区域提取和匹配特征点。本文的算法流程如图1所示。

2.2 重叠区域估计

（1） 图像预处理

输入两幅图像后，首先进行灰度化，再进行双边滤波。相较于高斯滤波，双边滤波的优势在于去除图像噪声的同时能较大程度保留边缘特征信息。本文模板尺寸取15*15，空间距离权重模板方差取20，相似性权重模板方差取50。

相比于单纯的灰度二值化，梯度图更能对特征进行描述，且具有光照不变性，梯度图提取本文使用sobel算子。

使用自适应阈值算法对其二值化。阈值矩阵计算，本文选用高斯滤波模板，模板尺寸取15*15，常数项取-2。对大于阈值的点设为255（白色） ，小于则设为0（黑色） ，即可得到二值梯度图。

一般来说，得到的梯度图白色区域较细，可以对二值梯度图进行膨胀处理，本文膨胀核尺寸取5*5。为了缩短计算时间，将二值梯度图的高度压缩1/2。图像预处理效果如图2所示。

（2） 重叠区域位置估计

若事先知晓要进行图像拼接，在拍摄图像的时候，通常是以自身为旋转点，每拍摄一张图像就横向旋转一定的角度，或者是进行横向平移式的拍摄。基于此，可以针对性地对重叠区域位置进行估计。

图像分割的份数取20，垂直滑动单向次数取10，则水平滑动总重合次数为39，垂直滑动总重合次数为21，通过对符号的使用，滑动取方差估计重叠区域位置算法的步骤如下：

输入：两张大小相同的图像src1和src2。

输出：src1和src2的估计重叠区域子图像。

1） 对src1和src2进行预处理，得到高度压缩为1/2的二值梯度图img1和img2;

2） 将img1和img2按src1->width/20列的跨度进行水平滑动，每次重合的区域记录到数组hOverlap1[i]和hOverlap2[j]（i，j = 0，1，2，…，39）;

3） 取出hOverlap1[i]和hOverlap2[j]（i=j）按src1->height/200行的跨度进行垂直滑动（即在纵向1/5的区域内滑动） ，每次重合的区域记录到二维数组vOverlap1[i][k]和vOverlap2[j][l]（i， j = 0，1，2，…，39; k， l = 0，1，2，…，21）;

4） 计算|vOverlap1[i][k] - vOverlap2[j][l]|（i=j， k=l）的方差，记录到二维数组vStdDev[u][v] （u = 0，1，2，…，39; v = 0，1，2，…，21）;

5） 找出vStdDev[u][v]（u = 0，1，2，…，39）各一维数组的最小值，记录到数组hStdDev[m]（m = 0，1，2，…，39）;

6） 找出hStdDev[m]的最小值Shmin，并获得其元素序号idx;

7） 将src1和src2按src1->Width/20列的跨度进行水平滑动，每次重合的区域记录到数组overlap1[i]和overlap2[j]（i，j = 0，1，2，…，39），并将overlap1[i]和overlap2[j]（i=j=idx）作为估计重叠区域;

8） 从数组hStdDev[m]中删除最小值Shmin并计算均值M，然后计算M-Dhmin，若差值小于阈值t1则不信任估计重叠区域并退出算法，若大于阈值t1则进行下一步。

9） 若估计重叠区域面积占比小于30%，则将估计重叠区域调整为对应的30%面积区域，然后返回估计重叠区域子图像。

滑动示意图如图3所示，靠左边的图表示右滑和上滑的图像，靠右边的图表示左滑和下滑的图像，中间交叉部分表示重合的区域。

为了保证算法的效率，在滑动时只按一定跨度进行滑动。为了保证方差相似度的質量，M和Dhmin的差要大于阈值t1，以及重叠区域面积占比设置下限为30%。垂直滑动跨度取src1->High/200行，是由0.2*0.5*src1->height/20计算得来，0.5是因为高度压缩了1/2，0.2是为了能在纵向1/5的区域内搜索。为了减少计算量，可以用标准差值代替方差值表示相似度。

2.3 图像配准

相比于SIFT（Scale-invariant feature transform），SURF在抗干扰和计算速度上更有优势[9]。本文为了兼顾计算时间和特征不变性，故采用SURF。为了减少特征点提取的计算量，本文将图像分割为20份并行计算，同样也是为了配合算法1中的水平滑动跨度。图像对数量阈值设为t2。特征点匹配方面，为了提高匹配对的质量，在构建k-d树的基础上进行了比率检验和交叉检测[10]，然后使用RANSAC算法[11]得到内点。

（1） 单应矩阵与内点计算

利用齐次坐标进行变换，匹配点对有如下变换关系：

[h1h2h3h4h5h6h7h8h9uv1=u'v'1] （1）

等式左边的大矩阵是单应矩阵H，其自由度为8，即4个匹配点对就可以计算出h1～h8的数值，h9取1即可。将单应矩阵以向量形式h转换为齐次线性最小二乘问题Ah=0后，应用最小二乘法求解。

RANSAC算法的核心思想是每次抽取s个匹配对，抽多少次才能保证有一次不是外点的概率为q。基于此，对数变换后可得如下关系式：

[N=log1-qlog1-1-εs] （2）

式中，N表示迭代抽取的次数，s表示每次抽取的匹配点对个数，ε表示匹配点对总量与外点对的比例。本文中s取4，因为至少需要4个匹配点对才能计算出单应矩阵。q需要事先确定，q越大，则抽取的匹配点对为内点的可能性就越大。ε由单应矩阵的重映射误差得到，重映射误差d的计算式如下：

[dp'，Hp=||p'-Hp||]

[=u'-h1u+h2v+h3h7u+h8v+h92+v'-h4u+h5v+h6h7u+h8v+h92]

（3）

每次选取4个匹配对后，计算单应矩阵H，再利用H对所有的匹配对进行重映射误差计算。[e=i=0nd2i]，设置阈值η，若e小于该值，则认为该对匹配点是内点。得到ε后，带入式（2），更新最大迭代次数N，直到满足迭代次数或已得到最大的内点数量时，则退出迭代。

（2） 鲁棒校验

通过贝叶斯公式，计算后验概率（一对匹配点是内点的情况下图像有重叠区域的概率） 。设置阈值pmin，若后验概率大于pmin，则认为输入的两幅图像是有重叠区域的[12]。基于此，本文使用如下的置信度计算公式对估计重叠区域进行评估：

[c=ni8.0+0.3nf] （4）

式中，ni表示内点匹配对的数量，nf表示总匹配对数量。设置阈值ηc，若置信度大于ηc，则认为重叠区域估计成功。

3  实验结果与分析

为了验证本文算法的有效性和准确率，对20对图片进行了实验，实验图片组如图4所示，图像的尺寸均为1000*1000。实验程序的运行环境为i5-6300HQ（四核） 、Windows10和Visual Studio 2015，程序实现方式为C++语言和Opencv3.3.0。

3.1 估计方法有效性验证

（1） 估计成功图像对实验结果与分析

限于篇幅，表1比较了估计成功的5对不同估计重叠区域面积图像对在SIFT算法、SURF算法和本文算法特征点和匹配对个数的结果，表2为表1的计算时间比较。实验结果表明，在估计成功的情况下，随着重叠区域面积的占比降低，本文算法大大减少了特征点的提取数量以及计算时间，提升了匹配对占比，且没有降低图像配准的准确性。

以估计成功的实验图7、2和14为例，本方法位置估计的匹配和拼接结果如下图5所示，半透明区域为估计的非重叠区域。

（2） 估计失败图像对实验结果与分析

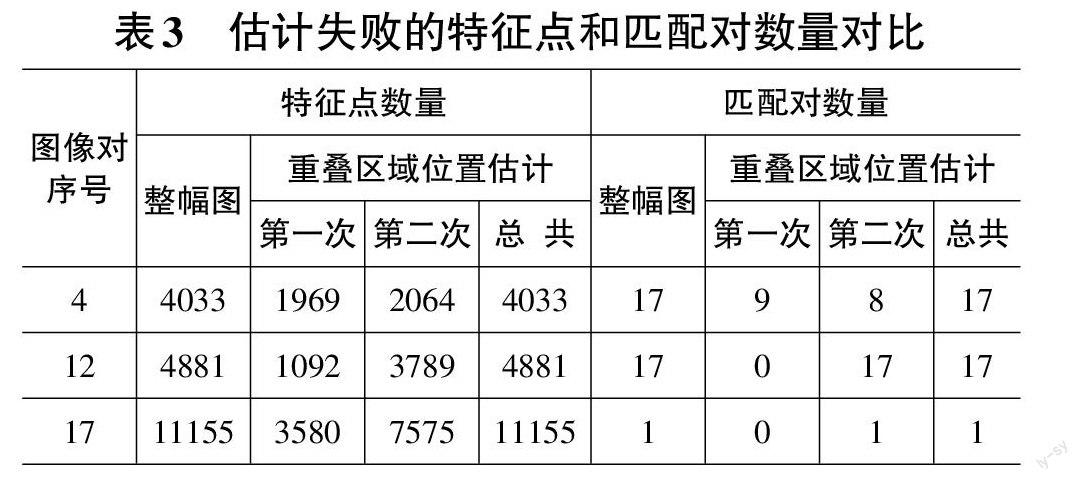
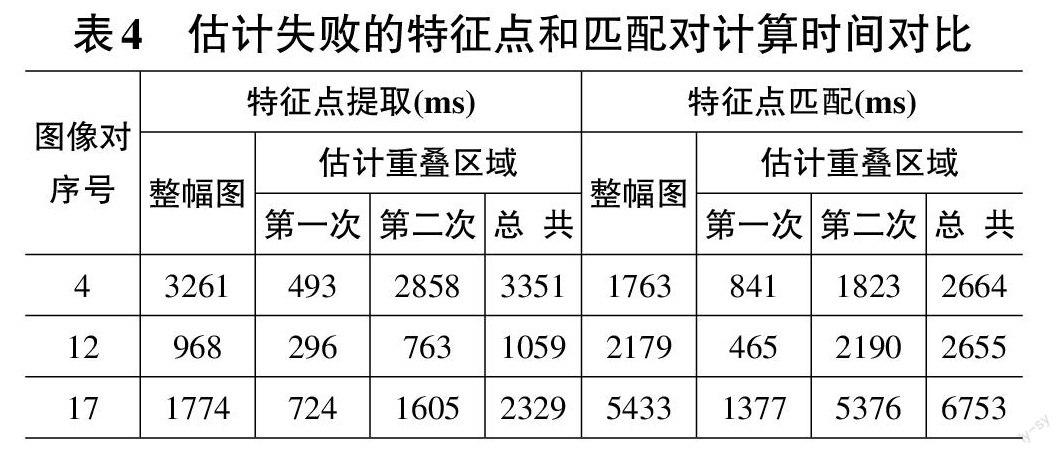
表3比较了本方法重叠区域位置估计失败的3对图像在整幅图和本文算法计算时的特征点和匹配对数量。对整幅图的计算也采用了并行计算方式。可以看出，第一次得到的匹配对数量都很低，原因是完全没有相似区域或者相似区域面积较小。表4是表3的计算时间对比，可以看出，因为多了一次对部分无效特征点的匹配，所以总的计算时间反而有所增加。

分析估计失败的原因，序号4图像对的画面内容是天空和草地，边缘特征信息较少，序号12图像对的画面内容是一座高楼，存在较明显的旋转关系，序号17图像对的画面内容是树林，边缘特征信息太多且没有区域性，即本方法在不存在旋转和透视关系、边缘特征信息较为丰富且具有左右区域差别的情况下具有较好的估计准确性。

图6对比了20对图像分别在使用穷举匹配法、Lowe的方法和本方法时的图像拼接计算时间，可以看出，在估计重叠区域失败的情况下，虽然会增加额外的计算时间，但从整体来看，本方法还是能减少大批量图像拼接的计算時间。

3.2 估计方法比较

作为同样采用图像处理方式对重叠区域进行估计，以此提高图像配准效率的方法，且无其他相同性质的估计算法情况下，本文估计方法将只与文献[7]的估计方法进行对比。据文献[7]所述，将图像预处理中的中值滤波核尺寸和自适应滤波核尺寸设置为21，其他未提及参数则与本方法的设置相同。实验样本用上述20对图像，对比估计都成功、文献[7]方法失败但本方法成功和文献[7]方法成功但本方法失败三种情况的结果，以此验证不同估计方法的差异性、准确性和有效性。估计成功的标准是，估计的重叠区域面积占比和实际的偏差不能太大，且拼接效果较好，实际占比由人工根据图像对标定。

图7对比了两种估计方法的误差，由实际占比减去估计占比得到，0处横线表示实际占比。可以看出，本文方法的准确性较好。

图8对比了两种方法的匹配对和特征点数量比值总和，能直观体现出两种估计法的有效性，且本文估计方法较好。

表5比较了文献[7]和本文的估计方法计算时间。因为本方法相较于文献[7]方法更适合并行计算，所以本方法计算时间较少。

4 结束语

本文针对图像拼接中特征点提取和匹配耗时长的问题，提出了重叠区域位置估计算法，该算法是基于含有边缘特征信息的二值预处理图像，在水平和垂直方向滑动计算方差，先估计图像对重叠区域的位置，然后只对估计区域进行特征点提取和匹配，从而提高图像配准的效率。另外，利用条件限制和鲁棒校验配合估计算法，从而提高整体图像拼接的有效性。

实验结果表明，在大批量图像拼接时，本文提出的算法能有效提高图像配准的效率，但目前该算法对左右区域边缘特征差异不明显、存在透视关系和垂直方向偏移大的图像对表现不良，故下一步将进一步优化提出的算法，以应对多种拍摄情况的图像对。

参考文献：

[1] Liu Q X，Su X Y，Zhang L，et al.Panoramic video stitching of dual cameras based on spatio-temporal seam optimization[J].Multimedia Tools and Applications，2020，79（5）：3107-3124.

[2] 任靖娟，王玖炜，曹莉.VR全景视频制作软件目标可视化三维虚拟仿真[J].计算机仿真，2020，37（9）：299-302，311.

[3] Ro S H，Kim S H.An image stitching algorithm for the mineralogical analysis[J].Minerals Engineering，2021，169：106968.

[4] Harris C G ， Stephens M J . A combined corner and edge detector[C]// Alvey vision conference. 1988.

[5] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60（2）：91-110.

[6] Bay H ， Tuytelaars T ， Gool L V . SURF： Speeded up robust features[J]. Proceedings of the 9th European conference on Computer Vision - Volume Part I， 2006.

[7] Qu Z，Li J，Bao K H，et al.An unordered image stitching method based on binary tree and estimated overlapping area[J].IEEE Transactions on Image Processing，2020，29：6734-6744.

[8] Qin Y ， Li J ， Jiang P ， et al. Image stitching by feature positioning and seam elimination[J]. Multimedia Tools and Applications， 2021（3）：1-13.

[9] 赵春江.图像局部特征检测和描述基于OpenCV源码分析的算法与实现[M].北京：人民邮电出版社，2018：78 -88.

[10] Vincent E ， Laganire R . Matching feature points in stereo pairs： A comparative study of some matching strategies[J]. Machine Graphics and Vision， 2001， 10（3）：237-259.

[11] Choi J ， Medioni G . StaRSaC： Stable random sample consensus for parameter estimation. CVPR[C]// DBLP. DBLP， 2009.

[12] 赵毅力，夏炎.无序图像自动匹配与识别[J].计算机应用与软件，2014，31（12）：262-264，310.

【通联编辑：光文玲】