Temperature prediction model for a high-speed motorized spindle based on back-propagation neural network optimized by adaptive particle swarm optimization
2022-10-18LeiChunliZhaoMingqiLiuKaiSongRuizheZhangHuqiang
Lei Chunli Zhao Mingqi Liu Kai Song Ruizhe Zhang Huqiang
(School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China)
Abstract:To predict the temperature of a motorized spindle more accurately, a novel temperature prediction model based on the back-propagation neural network optimized by adaptive particle swarm optimization (APSO-BPNN) is proposed. First, on the basis of the PSO-BPNN algorithm, the adaptive inertia weight is introduced to make the weight change with the fitness of the particle, the adaptive learning factor is used to obtain different search abilities in the early and later stages of the algorithm, the mutation operator is incorporated to increase the diversity of the population and avoid premature convergence, and the APSO-BPNN model is constructed. Then, the temperature of different measurement points of the motorized spindle is forecasted by the BPNN, PSO-BPNN, and APSO-BPNN models. The experimental results demonstrate that the APSO-BPNN model has a significant advantage over the other two methods regarding prediction precision and robustness. The presented algorithm can provide a theoretical basis for intelligently controlling temperature and developing an early warning system for high-speed motorized spindles and machine tools.
Key words:temperature prediction; high-speed motorized spindle; particle swarm optimization algorithm; back-propagation neural network; robustness
High-speed computer numerical control(CNC) machine tools are the technical foundation of the equipment manufacturing industry. As the core component of CNC machine tools, the technology and performance of the motorized spindle unit affect machine tool development. As a highly integrated spindle, the power loss of the motor and the friction heat of the bearing of a motorized spindle are the main heat sources. The thermal character directly affects the machining accuracy and service life of motorized spindles and machine tools[1]. According to statistics, the error caused by the thermal deformation of machine tools accounts for 40% to 70% of the total manufacturing error in precision machining[2]. The temperature increase is an important index for evaluating the high-speed operation of motorized spindles[3-5]. Therefore, developing motorized spindles inevitably requires accurate prediction and control of the temperature increase and thermal deformation to realize the automation and intelligence of motorized spindles[6-7]. However, because the thermal structure of spindles has complex boundary conditions and joint surfaces, large errors are obtained in the theoretical modeling and finite element analysis of their thermal design[8]. Temperature prediction is difficult because the temperature of the internal parts of a motorized spindle is not easy to obtain directly, and the temperature distribution of a motorized spindle is nonlinear and complex, resulting in the low accuracy of the predicted temperature. Therefore, the temperature increase characteristics of spindles must be obtained through a thermal balance test, and the model parameters must be checked. Zhang et al.[9]proposed a prediction model of temperature increase in high-speed and precision motorized spindles, which was combined with the calculated results of the finite element model and test data to accurately predict the temperature field of a motorized spindle under different working conditions. A comprehensive prediction model was applied to forecast the thermal-mechanical behavior of a spindle-bearing system considering various bearing surroundings[10]. Liu et al.[11]introduced a BP neural network for the thermal error prediction of a five-axis machining center. Jian et al.[12]predicted spindle thermal deformation using the BPNN. Kumar et al.[13]presented a hybrid model based on particle swarm optimization (PSO) and an emerging extreme learning machine to forecast the temperature. The BP neural network based on the PSO algorithm was applied to predict the high-speed grinding temperature of titanium matrix composites[14]. Li et al.[15]established the spindle thermal error prediction model based on the improved PSO (IPSO)-BP neural network, and IPSO was used to optimize the parameters of the BPNN based on the genetic algorithm (GA). An adaptive neuro-fuzzy inference system was used to design two thermal prediction models for thermal error compensation in machine tools[16]. These models have high accuracy in predicting a temperature increase or thermal error. However, the above mentioned neuro network models still have deficiencies, such as a lack of population diversity and an inadequate design of learning factors, weights, and other parameters.
In this paper, a BP neural network model based on the adaptive PSO (APSO-BPNN) algorithm is presented to forecast the temperature increase of a motorized spindle. To improve the generalization ability and prediction accuracy of the APSO-BPNN algorithm, the key parameters of the PSO algorithm, the inertia weight and learning factor, are optimized, and the mutation operator is integrated to enhance the diversity of the population and improve the success rate of the optimization. Further, the prediction performance of the BP model, PSO-BPNN model, and APSO-BPNN model are compared, and the results show that the APSO-BPNN model has the best prediction accuracy and generalization ability.
1 Modeling Methods for Temperature Prediction of a Motorized Spindle
1.1 Basic BP neural network model
BPNNs are trained according to the error back-propagation algorithm, and they have been applied in many fields because of their parallel processing ability, fault tolerance ability, and nonlinear mapping. According to Kolmogorov’s theorem[17], a three-layer BPNN can approach any nonlinear function in theory. The main characteristics of a BP network are signal forward transmission and error back-propagation. Therefore, a BPNN can be used to establish the nonlinear mapping relationship between the temperature of motorized spindle parts and time, ambient temperature, and coolant temperature, and the node of the output layer is the temperature of the front bearing outer ring, the temperature of the rear bearing seat, and the temperature of the stator end.
The node number in hidden layer neurons is determined by
(1)
wherem′ andn′ are the numbers of nodes in the input and output layers, respectively, anda′ is a constant within [1, 10].
According to Eq. (1), the node number in a hidden layer is determined to be 8 by experiments in this paper. The number of iterations is 100, the learning rate is 0.1, and the target error value is 1.0×10-4. The transfer functions of the hidden layer and the output layer neurons are tangent S-type transfer functions (Tansig) and linear transfer functions (purelin), respectively. Trainlm is used for network training. Therefore, the structure of the BP network is determined as 3-8-1.
1.2 BP model based on the particle swarm optimization algorithm
Although the steepest descent method is adopted in the BP network algorithm, it has problems such as a slow convergence speed and low calculation accuracy, and it easily falls into a local minimum value. However, the PSO algorithm is a swarm intelligence algorithm based on population. It can realize the optimization search through the cooperation and competition between particles to avoid falling into a local optimum. PSO has a higher convergence speed and global optimization ability. Therefore, the PSO algorithm is adopted in this paper to optimize the weights and thresholds of the BP network.
In the PSO algorithm, the particles search in the solution space by following the current optimal particle. The PSO data are initialized as a group of random particles, and then the optimal solution is found through an iteration method. In each iteration, the particle velocity is adjusted based on individual and global extrema, which are composed of an inertial part, cognitive part, and social part. When each particle finds an optimal value, it updates its own speed and position using the following equations[18]:
(2)
(3)
wherevidandpidare the velocity and position of thei-th particle in thed-th generation, respectively;tis the number of iterations;ωis the inertia weight;c1is called the cognitive learning factor;c2is the social learning factor;r1andr2are two uniformly distributed random numbers independently generated within [0,1][19], andpbest_idandgbest_idare the individual and the swarm historical best solutions at thed-th generation.
1.3 BP model based on the adaptive particle swarm optimization algorithm
The BP algorithm optimized by PSO still has disadvantages, such as low search accuracy and easy premature convergence, which reduces the predictive accuracy. This result is mainly due to the phenomenon of particle convergence and the decrease in population diversity. Therefore, a BP neural network based on the adaptive particle swarm optimization (APSO-BPNN) algorithm is proposed, which improves the inertia weight and learning factor of the PSO-BP algorithm and integrates the mutation operator of the GA to improve the prediction precision.
1.3.1 Adaptive inertia weight
The inertia weight of a particle describes its ability to maintain the previous motion state. In the early experiments, it was set to a fixed value within [0.2, 1.2]. In fact, the inertia weight decreases not only with increasing iteration times but also with decreasing distance from the global optimum. When the inertia weight is reduced, the local optimization ability of the algorithm can be enhanced. When the inertia weight is increased, the global search ability of the algorithm can be increased. Therefore, the adaptive nonlinear dynamic inertia weight can avoid the algorithm falling into a local optimum and improve the search efficiency. When the fitness value of a particle is dispersed, the inertia weight decreases. When the fitness value is near the local optimal solution, the inertia weight increases. The calculation formula is shown as follows:
(4)
whereωmaxandωminare the maximum and minimum values of the inertia weight, respectively;fis the fitness value of the particle;favgis the average fitness value;fminis the minimum fitness value.
1.3.2 Adaptive learning factor
Generally, the learning factorsc1andc2are set as fixed values in the PSO algorithm, and the self-learning ability and social learning ability of particles are considered equal. However, the search ability of particles in the early and later stages is easily affected byc1andc2. Therefore, to search in global space, an adaptive learning factor formula is proposed in this paper.
In the initial search stage of the PSO algorithm,c1is set to a larger value andc2is set to a smaller value, which makes the particles learn toward the optimal value, promotes the particles to obtain the best position in their history, and improves the local search ability of particles. In the later stage of the PSO algorithm,c1takes a smaller value andc2takes a larger value so that the particles tend to the global optimum to enhance the global search ability and the convergence speed. The improved formulas ofc1andc2are presented as follows:
(5)
(6)
wherecmaxandcminare the maximum and minimum learning factors, respectively;gis the current iteration number;Gmaxis the maximum number of evolutions.
1.3.3 Adaptive mutation operator
The GA is a computational model used to simulate the biological evolutionary mechanism of nature proposed by Holland[20]. The mutation operator can increase local random search ability and accelerate the convergence speed of the algorithm to the optimal solution. In addition, it can effectively increase the diversity of the population and prevent premature convergence. Therefore, the mutation operator is introduced into the PSO-BPNN algorithm. When the mutation operator is used, particles are reinitialized with a certain probability after each update to increase the disturbance of the algorithm and prevent it from falling into a local minimum. At the same time, the mutation operator is embedded in the PSO-BPNN algorithm to expand the population space reduced in the iterative process and search in a larger space to realize the adaptive adjustment of the operator and improve the accuracy of prediction.
Thej-th gene of thei-th individual is mutated as[21]
(7)
whereamaxandaminare the maximum and minimum bounds of geneaij;ris a random number within [0,1].
(8)
wherer2is a random number.
1.3.4 Calculation process of the back-propagation neural network optimized by adaptive particle swarm optimization model
On the basis of the PSO-BPNN algorithm, the adaptive inertia weight, adaptive learning factor, and adaptive mutation operator are introduced in the APSO-BPNN algorithm. The detailed procedure of the APSO-BPNN model is summarized as follows:
Step1Initialize the parameters of the particle swarm, including the number of iterations, population size, maximum and minimum velocities, and maximum and minimum positions. In this paper,tis initialized to 100, the population size is 30,vis within [-5,5],pis within [-10,10],c1is within [0.8,2.4],c2is within [2.4,0.8], andωis within [0.4,0.9].
Step2Substitute the initial weights and thresholds of the BP neural network into the PSO algorithm to initialize the particle velocities and positions and calculate the fitness value of the particle using
(9)
wherek′ is a coefficient;nis the training sample number of the BP neural network;yiis the actual output of thei-th node;oiis the predicted output of thei-th node.
Step3Compare the individual extremumpidand global extremumgidwith the fitness value. Iff>pid,pidwill be replaced byf; iff>gid,gidwill be replaced byf.
Step4Solve the adaptive inertia weight according to Eq. (4).
Step5Solve the adaptive learning factors according to Eqs. (5) and (6).
Step6Substitute the results of Steps 4 and 5 into Eqs. (2) and (3) and update the velocities and positions of the particles according to Eqs. (2) and (3), then update the fitness value of the particle.
Step7Carry out the mutation operation on the particles according to Eqs. (7) and (8) and update the individual and global extremum of the particle.
Step8Judge whether the termination condition is reached. If so, the optimized weight and threshold are substituted into BP neural network training. Otherwise, return to Step 4 to continue iterating.
Step9Judge whether the error between the predicted value and the actual value after training meets the termination condition. If so, the iteration will be suspended, and the prediction result will be outputted. Otherwise, return to Step 8 to retrain until the result outputs.
2 Temperature Experiments
On the basis of the test rig of a motorized spindle built by the research team, the thermocouple was embedded in the motorized spindle, and the temperatures of the front bearing outer ring, the rear bearing seat, and the stator end were measured. The temperature measuring points of the motorized spindle are shown in Fig. 1.

Fig.1 Temperature measurement points of a motorized spindle
The temperature values at three test points,the ambient temperature, and the coolant temperature of the motorized spindle at 12 000 r/min were measured. A set of data was collected every 15 s to ensure that the temperature of the motorized spindle could be recorded in detail until its running reached a steady state at this speed. A total of 340 groups of data samples were obtained after the preliminary processing of the experimental data. The temperature curves at this speed are drawn, as shown in Fig. 2. Fig. 2 shows that the motorized spindle reaches thermal balance at approximately 5 100 s. A nonlinear relationship between temperature and time is also apparent at the three

Fig.2 Temperature values of measuring points at 12 000 r/min
measuring points. Therefore, using BPNN to establish the relationship between spindle temperature and time, coolant temperature, and ambient temperature is reasonable.
3 Temperature Prediction of a Motorized Spindle
When the motorized spindle rotates at high speed, the change in its internal temperature has strong nonlinear characteristics, and an excessive temperature increase will affect the machining accuracy of the spindle and the machine tool. The temperature prediction of the spindle is of great significance for exploring the trend of temperature increase and providing effective control decisions. Therefore, the BPNN, PSO-BPNN, and APSO-BPNN algorithms are applied to the temperature prediction of the motorized spindle in this paper. All the experiments are carried out on the same machine with a 2.10 GHz Core 2 Duo CPU, 64 GB memory, and Windows 10 operating system.
3.1 Data processing
The 340 groups of experimental data are divided into two parts. First, the data are numbered; then, according to the method of sequential extraction, 1 group is taken out from every 5 groups, and 68 groups are obtained and considered testing samples. Second, the remaining data are arranged in order to form 272 groups for training samples. To eliminate the difference in the order of magnitude among all dimensional data, the data are processed using the data normalization method and transformed into a number within [0,1]. The maximum/minimum method is adopted in this paper. The formula is[22]
(10)
whereTminandTmaxare the minimum and maximum values in the data sequence, respectively; andTkis the temperature value at timek.
3.2 Temperature prediction and discussion
On the basis of the BPNN, PSO-BPNN, and APSO-BPNN models, the temperature increase in the three measurement points of the motorized spindle is predicted. The temperature increase of the front bearing is analyzed in detail, and the result is shown in Fig. 3.
Figs. 3 (a), (c) and (e) show that the predicted values of the APSO-BPNN model for the front bearing outer ring are in the best agreement with the actual values, and the temperature fluctuation is also finely predicted. From Figs. 3 (b), (d) and (f), the temperature prediction errors based on the BPNN model, the PSO-BPNN model, and the APSO-BPNN model are distributed from -0.43 to 0.49 ℃, -0.15 to 0.32 ℃, and -0.18 to 0.15 ℃,respectively. The APSO-BPNN model has the smallest errors and the highest prediction accuracy among the three models.

(a)

(b)

(c)

(d)

(e)

(f)
With the same approach, the prediction temperature and prediction error of the rear bearing seat are calculated using the three models. The temperature prediction errors based on the BP model, PSO-BP model, and APSO-BP model are distributed from -0.3 to 0.5 ℃, -0.2 to 0.25 ℃, and -0.1 to 0.2 ℃, respectively. Additionally, the prediction temperature and prediction error of the stator end by the three models are also calculated. The temperature prediction errors based on the three models are distributed from -0.4 to 0.6 ℃, -0.3 to 0.4 ℃, and -0.25 to 0.2 ℃, respectively. Therefore, it can be concluded that the prediction errors of the three temperature points forecasted by APSO-BPNN are the smallest, which proves that the APSO-BPNN model has a stronger generalization ability and higher predictive precision than the comparison algorithms.
To evaluate the prediction results more intuitively, the mean square error (MSE) function, mean absolute error (MAE) function, andR-squared are introduced. The MSE between the experimental data and prediction data is used to evaluate the change degree of data. The smaller the MSE value is, the higher the prediction accuracy of the model is. The MAE is used to reflect the actual situation of the prediction error.R2is used to reflect the fitting effect of the model. The larger the value ofR2, the better the fitting effect of the model. The calculation formulas are shown as[23]
(11)
(12)
(13)
The values of MSE, MAE, andR2by using the BP- NN, PSO-BPNN, and APSO-BPNN algorithms are calculated. The calculation results are shown in Tab. 1.
Tab. 1 shows that the MSE and MAE values of the APSO-BPNN model are the smallest among the three models, while theR2value of the APSO-BPNN model is the highest, which indicates that the APSO-BPNN model has the highest prediction accuracy and the best fitting effect.
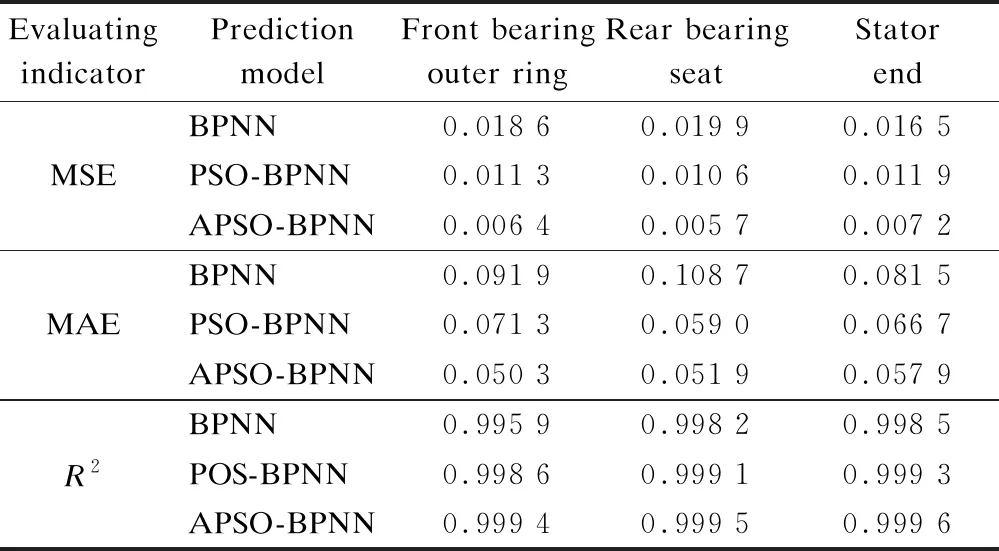
Tab.1 Evaluation of prediction models
4 Conclusions
1) The proposed temperature prediction model for a motorized spindle based on APSO-BPNN has a better prediction precision and generalization ability than those of the BPNN and PSO-BPNN models.
2) The adaptive inertia weight, the adaptive learning factor, and the mutation operator are integrated into the presented method, which improves the predictive accuracy of the method.
3) The proposed model has high prediction accuracy. However, how to feed back the prediction value to the existing control system for adjusting the parameters of the cooling and lubrication systems or early warning is future research work.
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Improved PBFT protocol based on phase voting and threshold signature
- Predictive current control system of PMSM based on LADRC
- Analysis on resonant shake table with novel variable stiffness mechanism
- BIM-based construction technologies for precast foamed lightweight concrete wallboards
- Analysis on degradation behaviors of sisal fibers at various pH conditions
- Application of polypyrrole nanofibers in the selective extraction of methotrexate and its polyglutamate metabolites from hospital effluents
