基于保证报价前提期和库存补货的供应链风险模型优化与设计*

周荣虎

(盐城工业职业技术学院，江苏 盐城 224005)

一、绪论

(一)提出问题

企业能够为客户缩短交货时间(交货时间)的能力是提高市场竞争力的有力武器。报价提前期(提价提前期)是指客户下订单时间与订单到期时间之间的间隔。不少专家强调了较短的提价提前期在吸引更多需求方面的作用。然而，客户不仅有兴趣获得更短的提价提前期，而且还有供应商重视提价提前期的能力。实际上，无论提价提前期的期限如何，如果供应商重视交货计划，企业可以有效地管理制造计划，它足以提前订购物品。但是，如果供应商并不总是能够在提价提前期内交付产品，可能会对客户有很多方面影响：缺货、制造延迟、高安全库存等。

企业重视提价提前期的能力正在成为竞争成功和生存的关键。企业必须确保每个订单的交货提前期(交货提前期)，通常定义为客户下订单和接收订单之间的经过时间，不得长于提价提前期，如果企业在供应链上没有持有库存，那么交货提前期等于总生产周期时间，即客户购买原材料，制造产品和分销产品所需的总时间。随着总生产周期时间的增加，如果供应链上没有库存则会增加交货提前期；而客户越来越需要更短的提价提前期，全球供应链必须保持相当大的库存水平以缩短交货提前期并满足交货时间约束：交货提前期≤提价提前期。在这种情况下，库存成本通常会显著增加。在复杂的供应链中，产品在不同的情况下生产，库存成本占总成本的很大比例(吴清一，2008)。因此本研究提出了以下三个问题：

第一，交货时间约束(交货提前期≤提价提前期)是否会导致重新思考并重新优化供应链的库存，或是否会影响供应链本身的设计。

第二，约束条件下，生产和分销的位置以及供应商的选择如何影响战略性的供应链决策。企业选择靠近客户区的生产区以便支持更短的交货提前期还是选择在遥远的低成本国家的生产区以便支持更低的成本。

第三，企业是选择高成本长期采购交货时间的当地供应商，还是选择远程的低成本供应商。

以上问题与许多企业都会遇到。Meixell(2005)强调，由于供应链中交货时间增加导致的成本权衡，尤其是全球化情况下使供应链决策更加复杂化。Barnes-Schuster等(2006)甚至认为，为了减少交货时间，公司更接近客户变得越来越普遍。为了研究这些问题，因研究需要将交货时间约束集成到供应链设计模型中，不考虑交货时间无法解决传统供应链设计模型问题。

(二)研究目标

为了研究交货时间对供应链设计的影响，在交货时间和库存补货约束下，开发了一种基于多级供应链设计的混合整数规划模型。模型保证重视与每个客户订单相关联的提价提前期以及在任何一对连续订单之间供应链的不同阶段中的不同库存的补充。假定一个确定性的离散需求过程，它接近企业与企业之间的许多实际情况，并假设不同情况下的库存策略。决策模型包括供应商的选择，生产和分销的位置以及供应链不同阶段库存水平，在每种情况下，不仅考虑产成品库存，还考虑原材料或半成品库存。

(三)研究意义

重要的理论价值和实践意义：①解决在同一模型中整合供应链设计的战略决策和提前期、库存相关的战术决策的问题；②考虑外部供应商的复杂多级供应链，可以在这些节点，配送中心和最终客户之间转移半成品的生产基地；③不确定情况下，涉及多个节点，在交货时间和库存补货条件下进行建模，这样复杂的供应链框架中不常见；④在现实案例研究中进行实验，以验证建模方法并获得结论，目的是了解交货时间和库存约束对供应链设计决策的影响。

(四)研究思路

Hammami和Frein(2014)开发了一种多级供应链设计模型，同时强制代表性客户订单的交货提前期必须小于或等于该订单的提价提前期，文献假设代表性订单满足交货时间约束，而不满足规划范围内的所有订单，没有明确指定该假设有效的条件。此外，Hammami和Frein(2014)仅考虑每个节点中每个产品都有一定级别的库存，而没有指定和模拟库存策略相关的假设。在实际情况下，由于诸如订单频率高，要保留的高库存水平等诸多因素，并不总是能够在两个连续订单之间补充供应链的不同阶段的库存水平。当顾客下订单时，配送中心的库存水平可能不足，这导致长交货提前期；但该模型假设配送中心总是有足够的库存，因而没有考虑这种情况。因此，模型解决方案可能不适用于某些实际情况。

通过模拟与库存补货相关的交货时间及其与提价提前期的相关性来重新审视Hammami和Frein(2014)的模型。此外，与Hammami和Frein(2014)不同，本文整合了在规划范围内按时交付所有订单的条件，明确地模拟了需求流程和采用的库存策略。建模框架中考虑了不同于Hammami和Frein(2014)使用的决策变量和约束。因此，本文的模型比Hammami和Frein(2014)的模型更现实，也更复杂。

二、文献综述

通过文献梳理发现相关文献从不同角度对定量供应链模型中的交货时间决策进行了研究。这些模型中的大多数不是处理供应链设计问题，而是假设事先给出供应链结构布局。文章首先回顾这种类型的研究，然后转向将交货时间集成到供应链设计模型中。

(一)交货时间运营管理和供应链的相关文献

Kapuscinski和Tayur(2007)在按订单生产配置下开发了交货时间报价模型，其中不能拒绝需求并且必须遵守提价提前期。随机需求在离散时间有限范围内到达，并且必须在提价提前期内满足，同时考虑可用容量。目标是尽量减少总预期成本。Pekgün，Griffin和Keskinocak(2008)将该企业的运营模拟为M/M/1排队系统，并考虑了线性交货时间和价格相关需求。通过适当的约束，确定最佳提价提前期和价格。Graves和Willems(2008)考虑了供应链在何处放置战略安全库存以最低成本为最终客户提供高水平服务的问题。他们假设每个阶段都采用定期审查基本库存，需求是有限的，并且每个阶段与其客户之间有一个保证的服务时间。Hammami和Frein(2014)在具有确定性需求的多级供应链环境中开发了库存放置模型，其中提价提前期必须得到重视，该文献假设有限的制造能力，并考虑制造订单在时间段之间的相互作用。此外，交货时间问题也是学者研究的焦点，上述论文涉及战术/运营生产计划(Spitter等(2005))和两级供应链中的采购/采购管理(Jha和Shanker 2009; Hammami和Frein 2012)。

此外，也有学者专注于研究供应链中交货时间的变异性。实际上，虽然需求不确定性是定量供应链文献中最广泛研究的内容，但管理交货时间变异性产生的不确定性也是至关重要的，特别是在全球化供应链中，其通常的特点是运输距离长、风险高、需求波动大。

Dolgui和Ould Louly(2002)在交货时间不确定性下研究了MRP方法的计划交货时间的最优值，目的是最小化预期的积压和持有成本；该模型提出了单级、多项、多期供应链问题，同时假设无限供应能力(交货时间不依赖于批量)和不断需求。Simchi-Levi和Zhao(2005)研究了具有三种网络结构的单产品多级供应链中的安全库存问题，其中每个阶段使用固定连续时间的基本库存策略来控制其库存。假设生产周期时间和运输交货时间是随机的、顺序的和外生的。Hnaien，Delorme和Dolgui(2010)开发了遗传算法来解决两级装配供应链中库存控制的多目标优化模型，其中交货时间被假定为随机离散变量。Hammami和Frein(2014)为供应商选择开发了一个优化模型，他们专注于低成本供应商的问题。

然而，当供应链是分析单位时，纳入交货时间变异性的研究相对稀少(Humair等2013; Bandaly等 2016)。Bandaly，Satir和Shanker指出，当交货时间是确定性参数时，研究交货时间对供应链性能的影响显然更为常见。Ben Ammar等审查交货时间不确定性下的供应计划和库存控制系统时得出结论，大多数具有随机交货时间的分析模型假设供应链(一个级别)和一个周期计划的简单结构。对于更复杂的过程，使用多级供应链和多个周期，分析方法将基于模拟的方法所取代。

(二)供应链设计模型中的交货时间的相关文献

本文将交货时间整合到供应链设计模型中，并解决在同一模型中将长期决策(设施位置，供应商选择)与短期/中期决策(库存放置和补货，交货提前期)相结合的难度。但是，现阶段将交货时间决策整合到供应链设计模型中的研究论文尚且不多，且多数集成交货时间的供应链设计模型都集中在配送设施的位置选址上。因此，多级供应链中不同阶段和产品之间的相互作用未充分得到考虑。特别地，他们不考虑模型决策中的外部供应商和制造设施。此外，购买的物品和中间产品也为得到充分考虑。例如，Daskin等(2002)处理了配送中心的位置，同时将目标函数中配送中心的工作库存和安全库存的成本纳入最小化。从供应商到配送中心的交货提前期被视为给定的输入参数(而不是变量)，并用于计算所需的安全库存。只有很少的文献将生产设施的位置整合到交货时间考虑的多级供应链设计模型中。其中一些包括最小化目标函数中的交货时间，而不是必须满足的服务约束。Arntzen等提供了该领域的先驱模型，主要决策变量是生产、库存和运输数量，交货提前期是供应链中每条链路上制造和运输所需天数，目标函数最小化交货提前期的总和乘以某个因子α和总成本乘以因子(1-α)，但该模型在决策和交货提前期的确定中没有考虑供应商问题。You和Grossmann(2008)在考虑生产基地和配送中心的位置的同时，为化工行业开发了供应链设计模型，但主要关注战术/运营问题(生产计划，运营计划)。该问题被制定为双标准优化模型，其目标是最大化净现值并最小化预期的交货提前期；预期交货交货时间计算为相应路径中产生的所有生产和运输交货时间的总和。在这项工作中，忽略了供应商的选择，因此忽略了与采购项目相关的交货时间。此外，在模型中仅考虑配送中心的最终产品库存。

将交货时间作为服务约束的多级供应链设计模型在文献中很少见。Funaki(2012)通过遵循Graves和Willems(2005)的网络模型方案，将战略安全库存放置模型与装配型供应链中的设施选址决策相结合。本文基于最后日期的需求并提出了有保证的服务水平，在计算服务时间时考虑了处理和运输交货时间。除了对供应链结构的限制之外，所提出的模型仅针对每个情况处理一个产品，并且假设供应链节点中的处理交货时间独立于处理的数量。

三、模型框架与假设

(一)供应链基本结构

考虑具有不同潜在外部供应商(S)、潜在制造设施(M)和潜在分销商(R)的多级供应链网络，用J表示所有潜在设施的集合(J =M∪R)。为了简化模型，考虑将单个最终产品交付给单个客户。考虑了获得最终产品所需的不同中间产品和原材料(原材料是指从外部供应商处购买的产品，中间产品是指供应链制造的产品)，所有涉及的产品的集合为P，用pf表示最终产品(pf∈P)。

制造企业j(j∈M)将一组输入产品(可以是原材料或中间产品)转换成一组输出产品。因此，j的输入产品从外部供应商获得，并且输出产品被输送到其他制造企业或配送中心。制造企业输出产品p所需的输入产品组用Я(p)表示。标量Φp′p表示每个输出产品单元p需要多少单位的输入p′。

对供应链中的梯队数量没有任何限制，上游企业可为不同的下游企业提供给定的产品。但是，假设供应链中的每个下游节点必须为每个给定的输入产品具有唯一的上游节点。显然，如果下游企业有多个输入产品，它可能会有不同的上游企业。

鉴于上述供应链结构，该模型非常适合制造型企业，例如汽车行业。实际上，制造商通常具有不同的组件和模块组装站点(半成品)。这些站点由不同的外部供应商提供，最终装配站点从企业的其他站点接收模块，并且从外部供应商处购买一些零件以组装成产品，商品最终运到配送中心。模型还可以代表电子行业中许多企业的运营，这些公司从供应商处购买零件并在运送到分销中心之前将其组装在内部。

(二)需求流程

本节通过真实业务案例，提出需求流程相关的假设。一家汽车电气线束制造商为中国的一家汽车制造商供货。每个星期五，汽车制造商都会下订单，并向供应商提供在未来4周内下达的实际订单以及8周内的需求估算。因此，在每周t的开始，供应商知道t，t+1，t+2和t+3的需求，并且可以预见到期间t+4，t+5，t+6和t+7的需求。此外，供应合同规定订单量不能大于最大值。供应商考虑此最大订单量进行长期生产计划(8周后)。汽车制造商下的每个订单必须在1周内交付。汽车制造商采用准时制，汽车制造商没有电子线束库存。不能在一周内交货对供应商而言代价非常高(如果出现延误，将支付高额罚款)。因此，供应商认为他必须满足1周的交货时间(不允许延期交货)。这种情况代表了汽车行业的一种常见情况。

在本研究中，假设客户订单是在规定范围内定期产生(例如每周一次)。用L′表示连续订单之间的时间间隔。如果订单每周放置一次，则L′= 1周。将计划范围划分为不同的持续时间段L′，在每个期间的开始处放置一个客户订单。每个客户订单都与订单大小相关联。令d表示客户下订单的最大限度，规定范围内的总需求由D表示。企业为每个订单Δ引入交货时间，假设参数L′，d，Δ和D是已知的。计划范围内的总需求将用于战略规划，而与期间相关的需求参数将用于计算交货时间和库存。需求流程如图1所示。

图1 需求流程

(三)库存策略

考虑基本库存策略，工厂j(j∈J)中给定产品p(p∈P)的相同库存水平必须在每个周期的开始(当订单下达时)可用。如果考虑给出的条件(1)和(2)，则应保证计划范围内的所有订单将按时交付，即每个订单的交货提前期≤提价提前期。

条件1：假定与最大尺寸d的顺序相关联的交货提前期必须小于或等于提价提前期。

条件2：保证每个工厂的每个产品的基础库存水平可以在每一对连续的周期之间，即在L′时间段内得到补充。

以上条件将包含在模型中，最后注意每个工厂中每个产品的基本库存水平不是事先确定的，而是由模型决定的。

(四)交货时间

确定与大小为d顺序相关的交货提前期。为了计算交货提前期，考虑了整个供应链的采购、制造和运输的不同交货时间的基础上。使用以下表示法：

将制造交货时间建模为加工数量的函数，比许多库存放置模型中假设的固定加工交货时间更现实。为了计算交货提前期，需要对供应链控制策略做一些假设。

采购订单在每个周期的开始下达。在给定的时间段内，每个(制造或分销)工厂最多可以向其上游节点发送一份采购订单。

在开始交付流程之前，工厂必须等到下游节点所需的全部产品数量可用后才开始交付。对于提供多个下游节点的工厂，假设该工厂同时释放所有下游工厂的需求。然后，根据运输交货时间，在每个下游节点接收产品。

在开始生产输出产品之前，制造工厂必须等待所有需要的输入项目数量都可以用。

(五)示例：模型决策和交货提前期

为了解释模型决策如何影响交货提前期，如图2所示。假设有两个潜在的供应商(s1和s2)，两个潜在的制造工厂(m1和m2)，两个潜在的分销工厂(d1和d2)和一个客户k。考虑1个最终产品p，假设是从购买的商品q制造的，例如Φqp=1。购买和运输交货时间在网络的不同弧线上方指示。在该说明性示例中，m1和m2中的制造交货时间等于每100个制造物品的1个时间单位。取d=100，d是最大订单大小。

图2 模型决策和交货提前期

下面讨论提价提前期的不同值的不同情况。

提价提前期=7。在这种情况下，对于任何可能的供应链配置和任何订单，总生产周期时间小于提价提前期，因此，所有订单都可以按时交货而无需持有库存。

提价提前期 = 6。例如，如果选择s1，m2和d2，那么不需要持有库存。但是，如果模型选择s1，m1和d1，那么生产周期时间将等于7。在这种情况下，如果没有库存，那么将有交货提前期> 提价提前期。可能有不同的解决方案，模型可以决定在m1中保持输入项q的100个单位。一旦收到p的订单(其数量不能大于100)，就可以在m1中以小于或等于1个时间单位制造所需的p数量，因为输入产品是可用的。然后，产品通过d1运送给客户，这需要3个时间单位。因此，交货提前期可以减少到最大值4，这保证了供应链可以满足提价提前期。

为了确保计划范围内的所有订单都能按时交付，每当下订单时(即每个期间的开头)，必须有一个100单位的m单位库存。最优库存水平由模型确定，这也确保了每两个连续期间之间的库存补充，以满足所有客户在计划范围内的订单。

提价提前期 = 1。在这种情况下，必须在d2中保留100个库存p并从d2交付客户。

显然，对于提价提前期的每个值，存在许多工厂位置或库存水平的可能性。最优解的解决方案在规划周期的供应链总成本减少到最低限度，同时确保交货提前期≤提价提前期为所有订单。

四、模型公式

根据问题情况的构建数学公式，主要的战略决策变量如下:

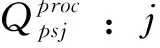
Hpj:基本库存水平(数量)的产品在工厂pj(j∈J)。这是每个时期开始时p在j中的库存水平。它还表示规划范围内j的p的平均库存水平。

该模型的目标函数最大限度地降低了计划范围内的总成本，包括设施运营成本、供应商选择成本、采购成本、制造成本、运输成本(设施之间)、交付成本(面向客户)和库存持有成本。考虑以下几点，不同成本因素的符号：

Oj：开放/运营设施j的固定成本;

Fs：选择/管理供应商的固定成本;

Upj：工厂j中产品p的单位制造成本;

Bpsj：来自供应商s的设施j的单位采购成本;

Tpjj′：从工厂j到工厂j′的产品p的单位运输成本;

Lj：从现场j到最终客户的最终产品的单位交付成本;

Ipj：在规划范围内持有工厂j中产品p的成本。

因此，目标函数由式(1)给出。

(1)

在本节的其余部分中，将介绍模型约束。通过关注与战略决策相关的约束制定交货时间和库存补货约束条件。

(一)与供应链设计相关的约束

首先将约束式(2)中给出的总需求D满足的计划范围。

(2)

约束式(3)遵守指配送中心的流量守恒条件。实际上，对于每个配送工厂，在计划范围内发送给客户的最终产品数量必须等于从中获取的制造数量。

(3)

(4)

(5)

正如建模框架部分中所解释的，强制规定每个下游节点(包括最终客户)对于每个给定的输入产品，必须有唯一的上游节点。这是由约束式(6)和式(7)保证的。

(6)

(7)

根据约束条件式(8)，选择供应商(即Ysupp= 1)，前提是且仅当供应商为一个产品提供至少一个产品时。其中，ψ指的是一个足够大的数量。

(8)

(9)

(10)

(11)

(12)

(二)交货时间和库存补充相关的约束

如前所述，为了保证所有客户订单都能在提价提前期内交付，规定与最大规模d订单相关的交货提前期必须小于或等于提价提前期，并确保基本库存每个工厂j中的每个产品p的水平(即Hpj)可以在每个连续的一期间之间补充。因此，首先需要确定生成的不同要求(对于所有工厂中的所有产品)当给定产品p和工厂j时，存在大小为d的客户订单，库存中有Hpj单位。

现在引入用于表示供应链上不同交货时间组件的符号。

λ：交货时间要求交付最终产品的数量d最终客户(λ是交货提前期对应于最大订单大小)；

图3 说明性案例

表1 交货时间变量和计算

1.由大小为d的订单触发的要求和产品流程

(13)

(14)

(15)

(16)

(17)

(18)

(19)

2.交货时间与库存补充

λ≤Δ

(20)

库存补充条件保证每个节点中每种产品的基本库存水平可以在每个期间结束之前补充。必须区分分销和制造节点的情况。实际上，只有最终产品由分销节点管理。因此，只向模型添加约束式(21)。

(21)

(22)

如果q是节点j的输入产品，则：

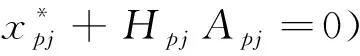
(1)如果p不是j的输出产品，则约束式(22)不起作用。

(23)

(24)

(25)

(26)

(27)

最后，在变量的域上添加约束。如式(28)所示。

(28)

(29)

五、实验设计与分析研究

实验旨在了解交货时间约束对供应链设计决策和总成本的影响。使用IBM WebSphere ILOG CPLEX软件解决模型。为了进行实验，使用某汽车公司(2015)提供的实际案例研究，同时为了研究标本具有代表性，作了一些调整。本案例研究涉及电气线束制造商(汽车行业)面临的供应链设计问题。最终产品是汽车驾驶舱线束，由不同的电线，电子元件和塑料部件组成。在总体水平上，考虑了11种购买的产品和7种中间产品。因此，产品总数为19(包括最终产品)。有4个潜在的生产基地：华北原产地和华南、华中、华东三个低成本地点。还考虑了一个潜在分销点，总共提供了四个潜在的分销节点，客户位于中国市场。这组潜在供应商可分为华东供应商、华南供应商和华中供应商，供应商总数是10，规划期内的总需求量为10000个单位。

(一)交货时间约束对供应链决策的影响

具体分析过程如表2-表4所示。

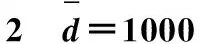
表和L′=4的解

表和L′=6的解

表和L′=8的解

(1)为了显示包含交货时间在供应链设计模型中的相关性，首先解决了模型的简化，其中删除了与交货时间和库存补货相关的约束(即只保留约束式(2)-式(12)处理供应链的常见配置。在这种情况下，获得的最佳解决方案是获得江苏制造和分销节点，并选择供应商S3、S5、S6、S8和S10。将该解决方案与使用的基本模型(表2-表5中提供的解决方案)获得的解决方案进行比较，表明交货时间约束影响供应链配置。在交货时间限制下，江苏制造和分销节点以及供应商S3、S5、S6、S8和S10的选择仅在L′= 12且Δ≥4.2的情况下是最佳的(如表5所示)。在所有其他情况下，选择不同的供应链配置。

表和L′=12的解

(2)最佳供应链设计决策不仅对提价提前期敏感，而且对客户订单频率也敏感。例如，可以看到，对于相同的Δ= 0.2，模型选择不同的制造节点L′= 6，L′= 8和L′= 12.。此外，对于相同的Δ= 4.6，模型选择相同的节点但不同L′=6和L′=8的供应商。

(3)尽管如此，虽然设计分散型的低成本供应链是可行的，但缩短提价提前期总是导致更局部的供应链。例如，在表2中L′= 4且Δ=1的情况下，该模型选择北京制造和分销节点，而不是选择其他可行的替代方案，例如从安徽制造和分销或在江苏制造和从北京分销。在这种情况下，补充库存的成本与北京地区相比不那么重要，这就解释了为什么该模型规定了这一决定。

(4)从0.25到5的整体价值，可以选择低成本的江苏制造地点并采用适当的配送节点以确保提价提前期。例如，可以看到模型在L′= 8和Δ= 0.2的情况下规定了该解决方案(如表4所示)。然而，尽管成本最低，但很少选择江苏制造基地。还可以观察到，当提价提前期变得更紧密时，所选择的分配节点变得更接近需求区。在的所有实验中都观察到了这一预期结果。

(二)交货时间约束对总成本的影响

图4 总成本的提价提前期 Δ函数

(1)当提价提前期非常紧(即Δ小)时，随着Δ的增加可导致总成本的显着降低。例如，当Δ从0.2增加到0.6时，可以观察到这种情况。因此，在这种情况下，企业可以通过引用稍长的交货时间来获得成本节约，这不太可能影响客户行为并且可以产生更高的利润。

(2)在某些情况下，不需要将提价提前期增加到一定水平以上，因为这不会产生任何成本节省。例如，在L′ = 4且L′ = 6的情况下，如果Δ增加到1.4以上，则总成本不会降低。这一结果与某汽车公司(2015)的研究结果相反。实际上，随着提价提前期值的增加，总成本总是在不断下降。然而，在模型中，与库存补货相关的现实约束可以消除较长提价提前期对降低总成本的影响。

(3)总供应链成本不仅对提价提前期敏感，而且对订单频率敏感。通过选择适当的订购频率，可以获得具有更长提价提前期的更小成本。例如，在的实验中，引用Δ=0.6，L′=4比引用Δ=1，L′=6或Δ=5，L′=8，成本更低。公司应该找到提价提前期和订单的最佳组合频率最低的成本。

在模型中考虑库存补充条件，影响了相关客户订单频率。回顾一下，L′表示两个连续订单之间的持续时间，这意味着1/L′是客户订单频率。对于不同的Δ值，在图5中最优成本的变化作为L′的函数。对图5的分析得出：

图5 总成本的L′函数

(1)与预期不同，实验表明，对于相同的提价提前期，有序频率的降低(即L′的增加)导致成本增加。结果表明，如果客户为较小数量的订单发出更频繁的订单，那么对公司来说可能会更好。

(2)当客户订单频率非常高时(此处，L′ = 2)，提价提前期不太可能影响供应链总成本。实际上，除了Δ=0.2的情况，由于必须选择北京市场成本相对较高，可以看出其他值的成本没有差别。实际上，该模型不能完全利用较长的提价提前期，因为它限制在短期内补充不同的库存。这解释了为什么在Δ=1，Δ=4.2和Δ=5的情况下获得相同的总成本。

(3)对于低频订单(此处，L′=12)，Δ=1，Δ=4.2和Δ=5的情况下总成本的差异不如预期高，这意味着提价提前期的影响不大。实际上，当连续订单之间的时间相对较长时，无论提价提前期的值如何，供应链都需要较少的中间库存。

六、结语

本研究开发了一种多级供应链设计模型，确保与每个客户订单相关联的提价提前期得到实现，同时明确地模拟供应链的不同阶段中连续订单之间的原材料，中间产品和最终产品的不同库存的补充。该模型的主要决策是：制造和分销节点的位置，供应商选择以及采购，中间和最终产品的库存定位。

使用该模型来研究提价提前期和客户订单频率对供应链设计决策和成本的影响。通过实验证明交货时间影响了供应链的最优配置，特别是关于节点位置和供应商选择的战略决策。讨论了交货时间如何在远处的低成本工厂和当地昂贵的节点之间进行权衡。例如，发现在许多情况下，交货时间限制并导致制造和分销地点靠近需求区，并选择本地供应商，尽管成本较高。实际上，选择这样的本地供应链配置所产生的额外成本被库存成本降低而获得的收益所抵消，因为当供应链不在地理上分散时，需要更少的库存来满足提价提前期并补充不同的库存。

本文解释了决策者如何使用结果向客户报出最佳交货时间并协商订单频率。例如，考虑其他库存策略(例如再订货点策略)以及将模型行为与不同库存策略进行比较将会更有意义。供应链通常受到不同类型的不确定性的影响，特别是在需求和交货时间方面。需求或交货时间波动可能影响生产计划。出于这个原因，根据客户订单的最大可能计算交货时间，这是减轻供应链中此类风险的一种方式。然而，重要的是要研究需求和交货时间的可变性，并了解它们对模型决策的影响。