渤海Y油田基于泰尔指数的纵向吸水差异性研究

2022-10-17冉兆航王传军姜立富张文俊

石油地质与工程 2022年5期

冉兆航，王传军，郑旭，姜立富，张文俊

(中海石油(中国)有限公司天津分公司，天津300459)

渤海注水开发油田一般采用多层合注合采的方式，导致层间矛盾突出，干扰现象严重[1-6]。学者们针对油井纵向产出不均衡进行了研究，定义层间干扰系数，用于评价产能并指导油田分层系开发[7-11]。油田开发表明，注入水的纵向差异对油田开发影响较大，评价并减缓吸水差异性可以从根本上降低层间矛盾。陈永生等人应用室内实验和现场试验资料分析了注水井层间干扰对油田开发的影响[12-14]；李明军等人建立了注水井纵向非均质储层吸水量之比的关系式，分析了纵向渗透率级差对高渗层及低渗层吸水能力的影响[15]；以上方法均无法实现定量评价，仅能应用于较为简单的储层类型，对于多层注水开发油田，应用效果较差。

渤海Y油田是典型的海上大型多层砂岩油藏，含油层位为新近系馆陶组，储层岩性为河流相陆源碎屑岩，油层厚度为63～151 m，油气分布及压力系统较复杂，纵向上存在多套油水系统，为构造型层状油藏。根据储层特征，将Y油田储层划分为三类，其中Ⅰ类储层厚度较大(大于5 m)，物性和连续性好，泥质含量低；Ⅱ类储层厚度为2～5 m，连续性中等；Ⅲ类储层厚度小于2 m，多为孤立薄层。Y油田生产资料表明，Ⅰ类储层物性好、厚度大，因而吸水比例高，油井端含水率较高(大于90%)，部分层存在水窜现象；Ⅱ类储层吸水、产出比例居中，含水率为60%～80%；Ⅲ类储层物性差、厚度薄，吸水比例低，因此水驱程度低，含水率较低(小于60%)。为了更好地开展精细注水工作，需要对目前的吸水差异性进行评价。

1 常用方法

石油行业常用于评价差异性的方法主要为级差、变异系数和洛伦兹曲线。为衡量注水差异性，表现出局限性，以厚度为1，3，7，10 m四层合采为例，分别对小层吸水量为10，30，70，90 m3和10，70，30，90 m3两种情况进行计算，结果如下：

(1)级差(吸水量)为最大吸水量与最小吸水量的比值。两种情况对应的吸水量级差相同，无法反映3 m和7 m两个小层吸水存在的不均衡性。

(2)变异系数为标准偏差与平均值的比值，其中标准偏差的计算公式为：

(1)

四个小层平均吸水量为50 m3，分别计算两种情况对应的变异系数，结果均为2。

(3)洛伦兹曲线是将各小层厚度占总厚度比例作为横坐标、各小层吸水量占总吸水量比例作为纵坐标，把对应的样本点投在图上并绘制曲线，曲线与直线C之间的面积占三角形OHL面积的比例代表不均衡系数，其中直线C代表完全均衡程度(图1)。曲线A和C之间的面积与曲线B与C之间的面积相等，表示计算的不均衡系数相同。事实上，曲线A中，薄层吸水比例偏高，厚层比例偏低；曲线B中，薄层吸水比例低，厚层吸水比例高，因此前半段，曲线A高于曲线B，后半段曲线B高于曲线A，表现出两种完全不同的吸水差异性，但计算得出的不均衡系数仍相同。

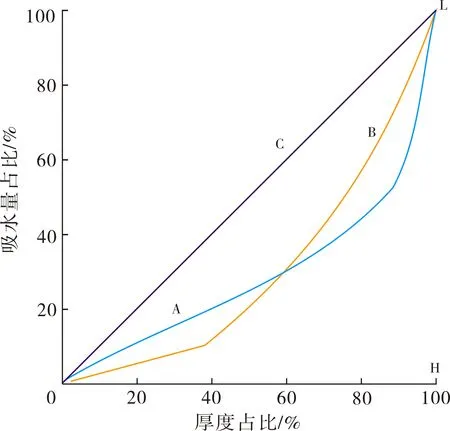
图1 两种吸水状况下洛伦兹曲线

以上几种方法只能从整体上表征多层吸水的不均衡性，为了更好地实现精细注水，并找出差异来源，需要寻找新的评价方法。

2 研究方法

荷兰经济学家Theil在1960年提出泰尔指数，以衡量个人之间或者地区间收入不平等，这一指数在经济学领域被广泛使用。泰尔指数[16-17]的计算公式为：

(2)

式中：D为总区域；c为区域的范围；Ec为某一区域对应的收入；Fc为某一区域对应的变量指数，如工业产值、人口等；E、F为总体值。泰尔指数越大，代表贫富差距越大。

纵向吸水差异性的泰尔指数计算公式如下：

(3)

式中：i为小层；N为小层总数；Qi表示小层吸水量；X表示要研究与吸水量对应关系的变量，文中代表渗透率K、吸水厚度H等。

①当X为某一变量时，T越大，表明纵向吸水差异越大；

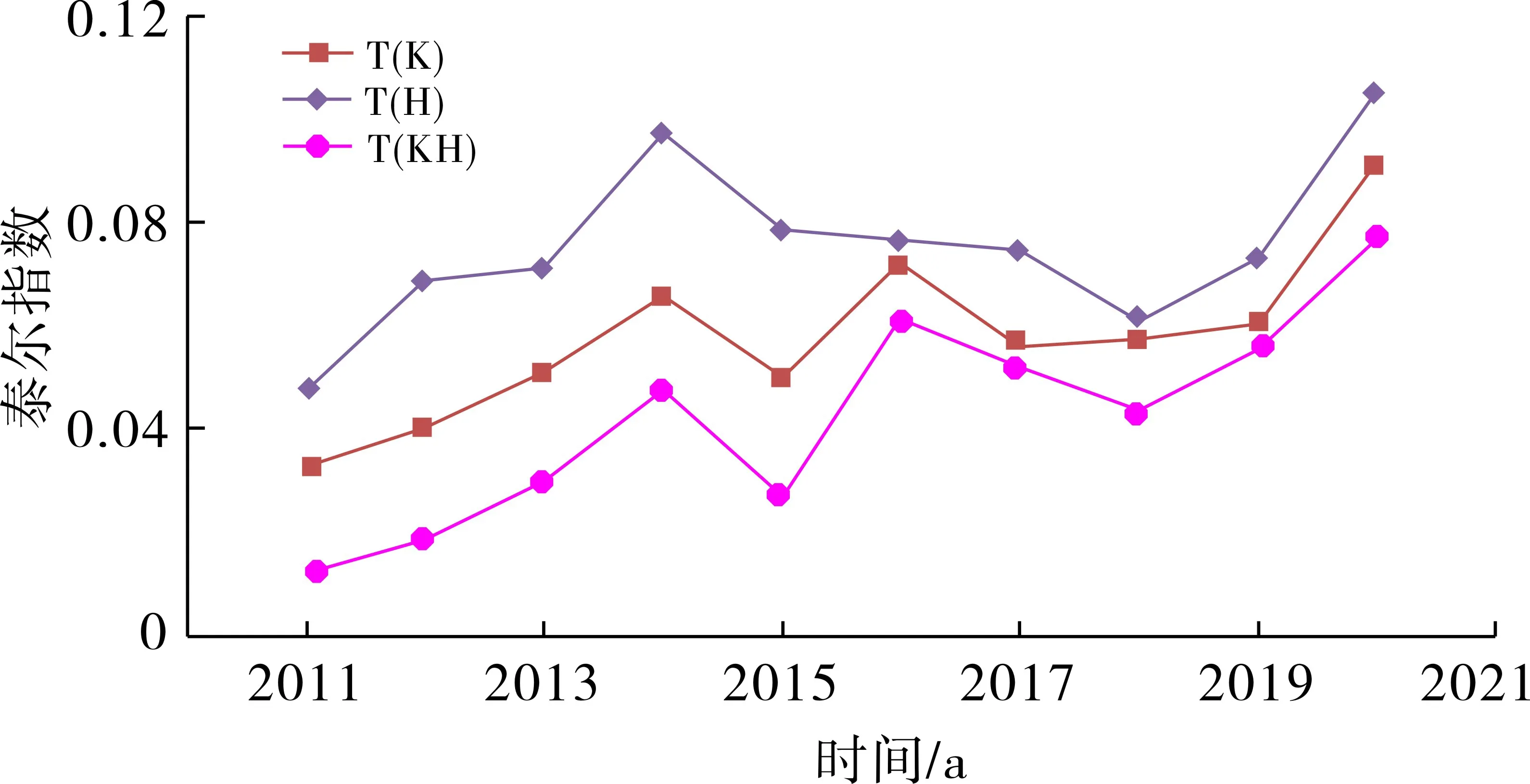
②当X为不同变量时，以T(K)、T(H)为例，T(K)表示变量为渗透率下计算的泰尔指数，T(H)表示变量为吸水厚度下计算的泰尔指数，若T(K)

③泰尔指数T可以分解为Tw和Tb，即T=Tw+Tb。

(4)

(5)

式中：Tw和Tb分别为某类储层内部和不同类型储层间的泰尔指数；j表示小层类型；Nj表示第j类储层总数；M表示储层类型总数；Twj表示第j类储层的泰尔指数；Q表示所有小层总吸水量；Qi表示第i小层的吸水量；Qj表示第j类储层的吸水量；Qij表示第j类储层中第i小层的吸水量；X表示变量的总量；Xi表示第i小层的变量；Xj表示第j类储层变量的总量；Xij表示第j类储层中第i类小层的变量。

④泰尔指数还可以进行不同类型储层间的贡献率(Wb)和某类储层内的贡献率(Ww)对总吸水差异的影响程度分析，Wb为储层间吸水差异对总差异的贡献程度；Ww为储层内差异对总差异的贡献程度。

Wb=Tb/T

(6)

Ww=Tw/T

(7)

此外，也可分析各类储层差异性对总差异的贡献率Wj，公式为：

Wj=(Qj/Q)×Twj/T

(8)

3 应用结果分析

3.1 差异性匹配关系研究

静态上，各小层渗透率(K)、吸水厚度(H)、地层系数(KH)均存在差异，利用泰尔指数，可计算吸水差异性与不同静态参数差异性的匹配关系。

针对Y油田69口注水井，通过参数K、H、KH计算注水井平均泰尔指数(图2)，结果表明，油田注水井吸水差异性逐渐增大，其中，2014年及2017—2018年大规模开展分层调配工作，一定程度上控制了吸水差异性。通过对比分析T(KH)

图2 不同静态参数下纵向吸水量泰尔指数对比

3.2 不同类型储层吸水差异性评价

为了找出Ⅰ类、Ⅱ类、Ⅲ类储层吸水差异性的主要来源，对泰尔指数进行分解，根据公式(4)、(5)可以计算某类储层内部的泰尔指数Tw，同时，也可得到三类储层间的泰尔指数Tb。

(9)

(10)

式中：T1、T2、T3分别为Y油田Ⅰ类、Ⅱ类、Ⅲ类储层的吸水量泰尔指数；Tw为三类储层内部泰尔指数总和；Tb为不同类型储层间的泰尔指数；X为K、H或KH。

从图3可以看出，Ⅰ类储层泰尔指数上升较明显，Ⅱ类储层泰尔指数下降较缓，Ⅲ类储层泰尔指数呈一定上升趋势。主要原因有以下几个方面：①油田早期以开采Ⅰ类储层为主，随着注水开发的深入，Ⅰ类储层水驱程度较高，地层经过长期冲刷，形成大孔道，水窜问题比较严重，个别主力小层吸水量大幅增加，造成Ⅰ类储层吸水差异性增大，泰尔指数逐年上升；②Ⅱ类储层物性、砂体厚度较为接近，且具有一定的注采连通性，因此泰尔指数相对平稳，呈一定下降趋势；③Ⅲ类储层注采连通性较差，油井端受效性也较差，因此，部分储层初期吸水多，后期吸水量持续降低，造成Ⅲ类储层吸水差异性增大，泰尔指数呈上升趋势。

图3 不同类型储层吸水量泰尔指数对比

从图4可以看出，不同类型储层间的泰尔指数总体呈逐年上升的趋势。Y油田目前已进入中高含水期(含水率为84.2%)，Ⅰ类储层形成大孔道，水窜问题越来越严重，吸水量大幅增加，而Ⅲ类储层注采连通性相对较差，吸水量持续减少，造成Ⅰ类、Ⅱ类、Ⅲ类储层间的吸水差异性逐渐增大。

图4 不同类型储层间泰尔指数对比

3.3 差异性贡献率分析

为了定量表征不同类型储层间吸水差异性对总吸水差异性的影响，利用公式(5)、(6)、(7)，可得到Y油田各类储层内及储层间吸水差异性对总差异性的贡献率。

Ⅰ类储层内部差异贡献率：

W1=(Q1/Q)×T1/T

(11)

Ⅱ类储层内部差异贡献率：

W2=(Q2/Q)×T2/T

(12)

Ⅲ类储层内部差异贡献率：

(13)

三类储层间贡献率：

Wb=Tb/T

(14)

W1+W2+W3+Wb=1

(15)

式中：W1、W2、W3分别为Y油田Ⅰ类、Ⅱ类、Ⅲ类储层吸水量泰尔指数贡献率；Wb表示不同类型储层间的泰尔指数贡献率。

由表1可以看出，Y油田吸水的总体差异主要是各类储层内(Ⅰ类、Ⅱ类、Ⅲ类)的差异带来的，储层间的差异占比相对较小，从2011年至2020年，储层间的差异贡献率逐年增加。在储层内差异中，Ⅰ类储层差异占比最大，Ⅱ类储层居中，Ⅲ类储层占比最小，从2011年至2020年，Ⅰ类储层内部吸水差异的贡献率逐年增加，Ⅱ类储层吸水差异的贡献率逐年下降，下降幅度较大，Ⅲ类储层吸水差异的贡献率逐年呈一定的下降趋势，目前已接近Ⅱ类储层的贡献率。通过分析可以得出以下结论：Y油田吸水差异性主要是由储层内差异引起的，而储层内的差异又主要来自Ⅰ类储层，同时，储层间的吸水差异也在逐年增加。