河套灌区渠系优化配水模型应用研究

韩宇， 邵梦璇，李彤姝，郭珊珊，孙志鹏，张明武

（1. 中国农业大学水利与土木工程学院，北京 100083；2. 北京师范大学水科学研究院，北京 100875；3. 清华大学土木水利学院，北京 100084；4. 黄河水利科学研究院，河南 郑州 450003）

中国现有灌溉面积达到了7 500.00万hm2，耕地灌溉面积达6 866.67万hm2[1]，农业作为中国的用水大户，其用水量达到了全国用水总量的62.1%[2]，其中，灌区农业用水主要来自渠系供水，但是由于存在灌排设施老化、灌溉水平落后等问题使得农业节水势在必行[3].当前许多灌区管理部门仍依据经验编制用水计划，往往造成渠系输水时间较长、渗漏量较大以及输水量较小等问题，灌溉用水效率因此无法得到提高[4].

当前，对于灌区管理水平的提高，尤其是调度管理水平的提升可大大激发节水灌溉潜力[5-6]的观点已达成共识.渠系配水是灌区调度管理的重要组成部分，通过模型优化等手段可以实现科学有效地输配灌溉用水，对灌区管理部门编制配水方案具有借鉴意义.

实现科学合理的配水过程可以减少渠道渗漏损失、提高灌区调度管理效率，对于缓解水资源短缺的压力、提高灌区水资源利用效率、改善灌区配水管理能力和实现农业的高效节水有着重要的意义[7-8].

各国研究人员针对渠系配水展开了大量研究，研究初期以人工规划方法为主：HALL等[9]以经济效益最大化为优化目标，提出动态规划模型为各用水部门提供水量配置决策方案.RECA等[10]建立了非充分灌溉下的水资源优化配置模型，但主观的相关规划没有统一的标准，并因掺杂了规划者主观因素，导致求解效率不高.人工智能的快速发展为求解复杂的水资源优化配置模型指明了新的方向.现如今，智能算法相较于传统的线性规划法、动态规划法等在计算精度与计算效率方面更加具有优势，成为一种新趋势.WARDLAW等[11]描述了一种基于遗传算法的优化方法用于灌溉水的实时分配，可以利用二次规划方法对目标函数进行求解.LIU等[12]为了优化渠道配水模型，建立了一种基于粒子群优化的自定义算法，可以克服典型启发式算法常陷入局部最优的问题.YAO等[13]基于遗传算法的优化模型提供了合理的渠道配水时间和流量安排，减少了水运损失.

之前的研究往往以配水时间或者配水过程中水量损失作为优化目标来建构渠系优化配水模型,并通过不同的智能算法求解，即单目标优化.随着算法的不断改进，优化配水模型逐渐向多目标优化发展：NIXON等[14]同时以闸门调节次数最少和上级配水渠道流量波动最小为目标建立优化模型,利用遗传算法求解.PENG等[15]将上级渠道流速波动变化最小以及上级渠道和分水渠渗漏损失最小作为优化目标，提出了一种在分水渠流量不相等的情况下简化渠系调度的多目标遗传算法优化模型.JIANG等[16]建立了基于过程的区域经济优化两级模型，将灌溉水利用效率最大和灌区经济效益最大作为优化目标.

回溯搜索算法、多目标粒子群算法以及向量评估遗传算法等算法在优化渠系配水过程方面得到了广泛的应用.目前灌区优化配水目标主要有两大类，一是以效益为主体，包括实现作物增产增收、增加农民经济收益[17]，或者是使管理部门供水成本最少、收取水费最多[18]；二是以渠系本身运行情况为主体，包括配水时间最短[19]、输水量最少[20]、输水损耗最低[21]、闸门开度适宜[22]等方面.为了提高河套灌区灌溉水利用效率、提升灌区相关部门调度管理水平，同时更加贴合灌区渠系配水实际情况，文中以河套灌区总干渠及其干渠为研究对象，以水流过渡平稳、渠系水渗漏量最小作为双优化目标，利用回溯搜索算法、多目标粒子群算法以及向量评估遗传算法优化渠系配水过程，最终得到各条干渠的配水时间分布，将3种算法的求解结果进行对比分析，选择较优的配水模型.

1 研究区域概况

河套灌区位于黄河中上游的冲积平原，是中国3个特大型灌区之一[23].灌区总面积为111.95万hm2，其中有效灌溉面积57.44万hm2，约占灌区总土地面积的51.2%[24].灌区年平均降雨量140 mm，年平均蒸发量2 000～2 500 mm，年平均温度为6～8 ℃，年平均日照时数为3 200 h.河套灌区总干渠下包括一干渠、乌拉河干渠等13条干渠, 现状渠系水利用系数0.58，渠床土壤透水指数为0.5，轮灌周期为30 d[25].河套灌区的灌溉时间为4—11月，期间包含夏灌期（4—6月）、秋灌期（7—9月）以及秋浇期（10—11月）.2020年总干渠引水时间从4月11日渠首放口开始，至11月21日关口结束.目前，总干渠以续灌为主；各干渠以轮灌为主，采取大轮灌小续灌、轮续结合的方式[26-27].总干渠及干渠设计参数如表1所示，表中Qd为设计流量，W为需水量，A为灌溉面积，Ld为长度.

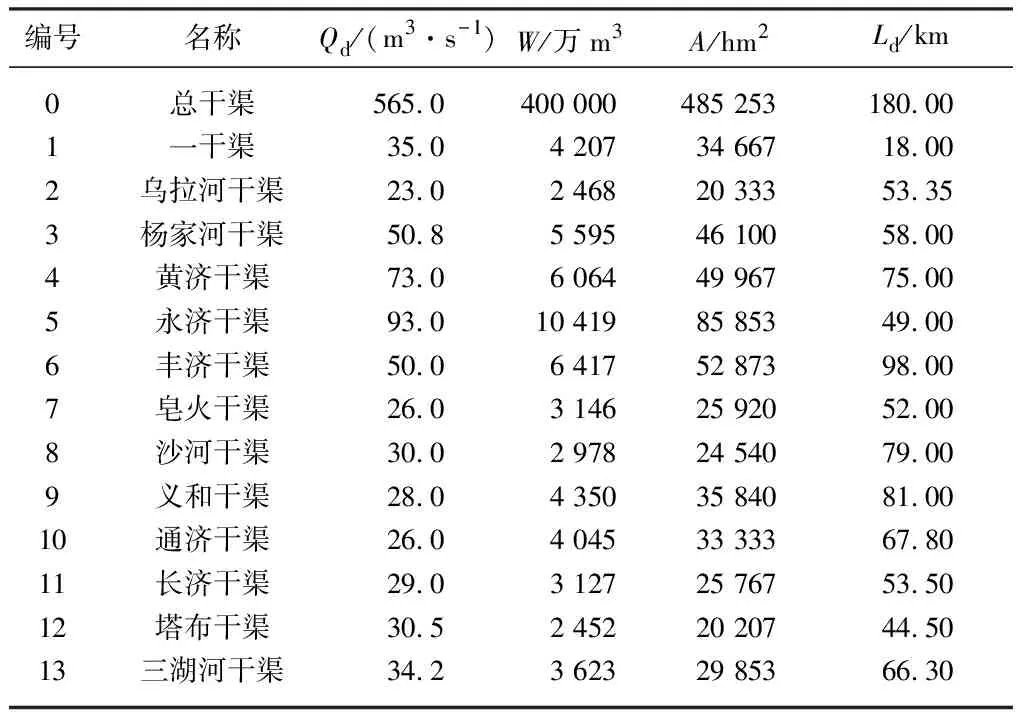
表1 河套灌区总干渠及干渠参数

2 研究方法

2.1 多目标多变量渠系优化配水模型

为使渠系优化配水模型更符合实际渠道输水情况，文中拟考虑水流过渡平稳、渠道渗漏量达到最小为优化目标，将配水时间作为决策变量，以此建立模型.目标函数如式（1），（2）所示.

（1）

（2）

约束条件为

1） 流量约束：

αdjQdj≤Q′j≤αujQdj,

（3）

γdqdu≤q′u≤γuqdu,

（4）

式中：qdu,Qdj为上、下级渠道设计流量,m3/s；q′u为上级渠道输水毛流量，m3/s；γd,αdj分别为上、下级渠道最小流量折减系数；γu,αuj分别为上、下级渠道加大流量系数;Au为上级渠床土壤透水系数.

2） 时间约束：

0≤t′j≤t″j≤T.

（5）

3） 水量约束：

（6）

Qj（t″j-t′j）≥MjSj,

（7）

（8）

式中：Wmax为允许可供水量,m3；Mj为下级渠道控制区域作物的灌溉定额,万m3/hm2；Sj为下级渠道控制区域作物面积,hm2.

（9）

模型中渠系渗漏计算采用经验公式，对于渠道最小流量与加大流量的约束系数采用经验系数，公式与系数参照《农田水利学》[28].

2.2 渠系配水优化模型求解

文中采用回溯搜索算法、多目标粒子群优化算法、向量评估遗传算法对渠系配水模型进行求解.

2.2.1 回溯搜索算法（BSA）

回溯搜索算法是Civicioglu在2013年提出的启发式优化算法，它根据最佳条件向前搜索以达到目标.BSA算法优点是结构简单、易于编程，仅预定义了1个参数，可依据历史信息引导种群进化， 但该算法的局部搜索能力较弱.具体步骤分为初始化、首选、突变、交叉、复选.

在进行渠系优化配水时，若Q为灌区总干渠总流量；α为渠道水利用系数，共有J条干渠，Qj为各干渠设计流量，Vj为用水量，不考虑渠道水损失，tj为各干渠灌溉时间，txm为第m次回溯后某干渠完成灌溉任务所需最短时间；第m次回溯后剩余流量Q′m，共进行M次回溯，总供水量为G；Rm为每次回溯后弃水量，R为总弃水量.

不考虑渠道水损失理想条件下，水量关系为

（10）

（11）

每次回溯后弃水量为

Rm=Q′mtxm,

（12）

总弃水R为

（13）

BSA优化配水思想：总干渠设计流量恒定条件下，求解干渠阀门开启情况，保持干渠以恒定流量连续稳定供水，当某干渠达到田间灌溉所需水量时关闭阀门，保证其余干渠流量连续恒定条件下再次运用BSA选择干渠，以此循环至所有干渠达到灌溉要求.R趋向于0，即代表可实现最佳配水.

2.2.2 多目标粒子群优化算法（MOPSO）

粒子群优化算法（PSO）是一种新型全局优化进化算法，它是源于对鸟群捕食行为的研究[29].PSO算法始于随机解，通过迭代发现最优解，并追随当前搜索到的最优值寻找全局最优.在一片区域内分布着大大小小不同的食物源，为了最终寻找到最大的食物源，即全局最优解，鸟群可以通过自身经验和群体之间相互传递的位置信息来不断地调整探索路径，使得整个鸟群都聚集在食物源周围.搜索到最适合觅食的地方就意味着找到了问题的最优解，问题收敛.MOPSO是基于PSO算法提出来的，高效便捷、初始化随机、求解速度快、全局搜索能力强.

2.2.3 向量评估遗传算法（VEGA）

向量评估遗传算法（VEGA）是第1个用于寻找1组非劣解的多目标进化算法[30].VEGA的主要思想是根据目标个数将每一代种群均分为数个子种群，子种群会根据不同的目标函数分配到1个适用值，子种群使用内部的选择算子进行筛选，交叉、变异得到新一代的种群[31].VEGA方法简单、容易操作，但得到的优化结果可能会有2个极端，一个是第一目标最优，第二目标尽可能优化，另一个则与之相反.因此应在模型求解中选择第1类的子代群体作为新一代种群进行迭代计算.

3 研究结果

3.1 模型参数

根据上述渠系模型，结合《农田水利学》[28]相关公式，确定模型系数，取值:上级、下级渠道最小流量系数分别为0.4，0.6；上级、下级渠道加大流量系数都为1.2，防渗措施折减系数为0.5；渠床土壤透水系数为3.4、渠床土壤透水指数为0.5.

河套灌区总干渠共有13条下级干渠，MOPSO和VEGA对应干渠将灌水起、止时间与配水毛流量设置为模型决策自变量，共39个决策变量；BSA对应下级干渠将灌水起、止时间设置为模型决策自变量，共26个决策变量；VEGA设置最大遗传代数为100.MOPSO选取包含1万个自变量定义域内随机初始点在内的初始点集，惯性权重定义为0.8，自我、群体学习因子定义为0.9.根据上述模型的约束分别设定灌水持续时间限制、配水毛流量区间和粒子更新速度的变化区间，进行模型的综合求解.

3.2 求解结果

文中通过综合算法参数以及《农田水利学》[28]相关参数，分别使用BSA，MOPSO和VEGA算法求解渠系模型，生成渠系分时灌水结果图.结果表明，BSA算法得到的灌溉时间为30.96 d，小范围超出规定值30.00 d，见图1a，图中B为干渠编号.MOPSO算法得到的灌水时间为11.65 d，相较于原来30.00 d的灌水周期均可以明显缩短配水时间，使配水效率得到提高，见图1b；VEGA算法计算得到的渠系灌溉时间为29.96 d，与原来灌水时间相近，但未能做到缩短配水时间，见图1c.

MOPSO和VEGA算法可以得到各干渠的毛流量，图2对比了2种算法下毛流量与设计流量结果.可见MOPSO算法所得毛流量相较于VEGA更接近于设计流量.

4 讨论与分析

4.1 基于模型求解结果的算法优越性分析

文中要求的灌溉时间为30.00 d，BSA，MOPSO和VEGA 3种算法得到的灌溉时间分别为30.96,11.65，29.96 d.BSA所得结果超出规定时间约1.00 d，MOPSO和VEGA均满足灌溉时间要求.BSA没有考虑到人工调度、阀门开度、渠系流量到达恒定流量的过程，在0时刻开始配水.因此文中以1.00 d作为流量变化的时间修正系数，使BSA所得结果向右平移1个单位.修正后，BSA配水时间为31.96 d，超出设定的轮灌周期，因此不建议采用BSA模型进行河套灌区优化配水过程模拟.MOPSO能够以最短时间11.65 d对渠系进行优化配水，从配水时间角度而言该算法最优.VEGA配水流量较小且配水时间较长，其原因可能是因为算法将保证渠系水流平稳作为了第一目标，但降低了渠道的整体运行效率, 相较于MOPSO算法不能明显缩短灌溉时间.另外，VEGA是一种随机搜索算法，参数设置大多凭借经验，并且没有清晰的收敛规则，可能导致在某一代时群体的适应度值已经不再变化，从而无法得到全局最优解.

MOPSO和VEGA算法均可以得出各干渠的毛流量，与设计流量相比，MOPSO比VEGA更接近设计流量.VEGA的毛流量小于MOPSO的毛流量，意味着VEGA流量小，配水时间长，说明这种配水方式更容易造成渗漏损失.这是因为在一定的时段内，渠道的衬砌情况和地下水水位可以视为不变，若下级渠道采用小流量长历时的配水方式，必定会增加上级渠道的输水时间[32]，造成水量损失增多.因此，从渗漏损失角度考虑，河套灌区更宜采用MOPSO算法得到的大流量短历时的优化结果.

4.2 基于统计参数的算法稳定性分析

目前灌区渠道阀门开启和闭合的自动化程度低、阀门开启对渠道水流稳定性影响较大，因此为保证灌溉期间水流输送的稳定性，阀门开闭时间应尽量集中.文中利用变差系数Cv、偏态系数Cs分析渠道配水过程中阀门开启和关闭的集中程度，进而探讨不同优化算法下水流的稳定性问题.

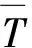
表2 各干渠阀门开启、关闭时间点偏离程度

4.3 基于水位变动影响的算法适用性分析

BSA算法采用“定流量、控开启”的原则，而MOPSO采用的是“定流量、变历时”，2种原则的不同之处在于各个干渠配水时间是否固定.BSA采用往年的灌水经验，给出了各干渠的总的配水时间，求解得到阀门开启时间点即可确定配水结束时间点；MOPSO没有给定固定的配水时间，配水历时可以改变，故各个干渠的配水时间以及开始、结束时间点的各次求解结果不同.由于黄河水位季节性变化，渠首引水量和各干渠引水时间往往会受到限制.四月中下旬至六月上旬是河套灌区作物需水量较大的时期，但是此时黄河上游地区干旱少雨，处于非汛期[33]，因此可能造成黄河流量变小，总干渠引水量可能相对减少.当引水量减少时，为保证配水过程中“有水可引、引水够用”，此时应该采用以往同时期的经验数据，固定配水时间，采用BSA进行优化；当某时段引水量充足时，此时建议采用MOPSO算法求解.

4.4 基于管理效率的算法合理性分析

由于技术限制等问题，目前阀门启闭仍主要依赖灌区管理人员控制.河套灌区面积大、渠道多，因此分区管理对于提升效率具有重要意义.根据配水时间集中程度以及干渠的地理位置分布情况对干渠实行分区，进行集中管理，有利于增强管理人员的可操作性，整体提升灌区的管理效率.BSA可以分为3区：1，2，4—7号干渠配水时间集中在前15 d，设为一区；3号干渠独立设为二区；8—13号干渠配水均开始于9 d以后，设为三区.同理，MOPSO可分为2区：1—6号干渠配水时间集中在前7 d，设为一区； 7—13号干渠配水时间集中在4—12 d，设为二区.VEGA不能明显看出分区结果.综上，针对BSA和MOPSO的优化结果可以进行分区管理，有利于提高整体管理效率；VEGA优化结果依据配水时间集中程度和干渠地理位置进行区域划分的界限不明显，不能得到较为理想的分区结果.通过算法优化手段获得的配水方案以及分区结果可作为参考方案提供给当地管理部门，但在实际的配水调度管理过程中，需综合考虑多方面因素的影响进行适时适量的调整，影响因素包括引水量年际变化、农民种植实际用水需求变化、管理部门人员部署调整等方面.

5 结 论

1） 以水流过渡平稳和渠系渗漏量最小作为2个优化目标，建立多目标渠系优化模型，同时以河套灌区作为研究对象，利用回溯搜索算法、多目标粒子群算法和向量评估遗传3种算法求解.求解结果表明： MOPSO配水时间为11.65 d，缩减为原要求灌溉天数的38.8%，大大提高了配水效率；VEGA优化效果不佳，不能明显缩短配水时间；BSA得到的灌溉时间超过要求的轮灌周期，并不建议采用此模型应用于河套灌区.

2） 基于同一渠系模型，以各干渠阀门开启集中程度作为评价水流稳定性的标准，并利用Cv,Cs进行衡量.3种算法结果进行对比分析，MOPSO和VEGA能更好地控制渠系配水过程中阀门相对集中开启，因此可以保证灌溉水在渠道运输中的稳定性.

3） 考虑渠首水位变化等因素，针对配水时间是否固定的问题对MOPSO和BSA算法优化结果进行了适用性分析，结果表明当渠首引水量较少时，需固定配水时间，采用BSA进行优化；当渠首引水量充足时，配水时间可不必固定，此时建议采用MOPSO算法求解.

4） 根据配水时间集中程度以及干渠的地理位置分布情况对3种算法优化结果进行管理区域划分，结果表明BSA和MOPSO算法优化结果便于实施分区管理措施，而VEGA优化结果不能得到较为理想的分区结果.