基于BP神经网络算法的路面结冰时间预测

朱强，徐强，付立

（1.交通运输部科学研究院，北京 100029；2.交科院公路工程科技（北京）有限公司，北京100013）3.山东高速青岛发展有限公司，山东 青岛 266114）

0 引言

近年来极端气候造成道路事故频发、路网瘫痪的情况日益突出和严峻。冰雪会导致路面抗滑能力大幅降低，削弱了道路的通行能力，容易产生恶性交通事故，使人们的生活和生产无法正常进行。对道路结冰进行预测预警，提前采取处置措施是保障冬季道路安全的重要措施。

国内外学者对使用神经网络算法预测是否达到结冰状态做了广泛研究。Kreutz 等基于SCADA系统采集的数据，使用神经网络对北欧等寒冷地区的风力发电涡轮是否处于结冰状态进行了预测[1]。He 等使用神经网络预测输电线路的结冰厚度，将结冰厚度分为多个层次，建立了卷积神经网络模型[2]。邱欣等使用SVM 方法，结合降水条件对不同路域是否结冰进行了预测[3]。魏扬等使用神经网络算法预测了飞机结冰[4]。赖军杰等使用神经网络对机场跑道是否处在结冰状态进行了预测，将机场跑道划分为结冰域、临界域和非结冰域三部分[5]，但并未预测跑道结冰的时间。池昊等基于SCADA 系统采集的风机叶片数据通过神经网络进行结冰预测，根据叶片运行状态判断是否到达结冰状态，准确率达到了95%[6]。杨鹏飞等采用粒子群算法、交叉验证算法和遗传算法对道路结冰进行了预测，经对比得出遗传算法优化后预测模型的通用性和准确度更高[7]。刘洪兰等通过BP 神经网络模型对静止水域和流动水域的结冰厚度进行预测，准确率达到80%左右[8]。李大中等使用优化的深度全连接神经网络模型，通过小批量的梯度优化算法Adam 识别风机叶片是否处在结冰状态[9]。熊竹等将降水量和温度作为基本条件模拟结冰形成的速度和结冰量，并通过BP 神经网络算法对结冰量进行了预测，但是没有对距离结冰的时间进行预测[10]。舒斯等对湖北地区高速公路多个监控点近2 年的结冰数据进行建模，计算每个监控点的结冰拐点值，当温度小于拐点值并发生降雨时，即认为路面已经结冰并进行报警[11]。综上可以看出，目前的研究使用BP 神经网络算法针对结冰预测开展了一些工作，说明BP 神经网络在相关领域有了初步应用，但还缺乏使用BP 神经网络对道路结冰时间的研究。事实上，基于道路的环境、地理因素和气象数据变化特点，建立预测模型并使用自学习的方法不断优化调整模型计算未来结冰时间，可在合适的时间采取措施避免结冰，不但能保障道路安全，还能节约人力、材料等养护成本，具有一定的经济意义。

鉴于此，本文基于BP 神经网络算法，将安装在路面的传感器每5min获取的路面信息作为历史数据，包括冰点温度、滑湿系数、含冰比例、路面状态、路面温度、含盐量、水膜厚度、时间等8 种特征信息。使用Pearson 方法对特征值进行特征选择，将历史数据分为两部分，一部分用来进行模型训练；另一部分作为验证数据，在训练完成后根据模型对训练结果进行验证和优化，并给出模型的测试效果。通过使用神经网络算法，综合运用多种气象、路面数据，为准确预测结冰提供一定的支持。

1 路面结冰数据预处理

1.1 结冰数据简介

近几年我国高速公路气象信息化越来越受到重视，多个地区的高速养护部门已经安装了路面传感器、路侧气象站等设备采集气象信息。安装在路面的传感器（见图1）可同时采集多种特征数据，包括：冰点温度、滑湿系数、含冰比例、路面状态、路面温度、含盐量、水膜厚度、采集时间、设备ID、地理坐标等（见表1）。其中“路面状态”包含多种情况：结冰、积雪、干燥、潮湿等，可根据其值判断当前道路为哪一种状态、是否结冰。取监测点结冰前一段时间除设备ID、地理坐标以外的8 种特征数据进行神经网络建模，以“路面状态”首次出现结冰的时间为“结冰时间点”，输入其他特征值进行模型训练，计算其距离“结冰时间点”的时延。

表1 路面结冰预警数据字段说明

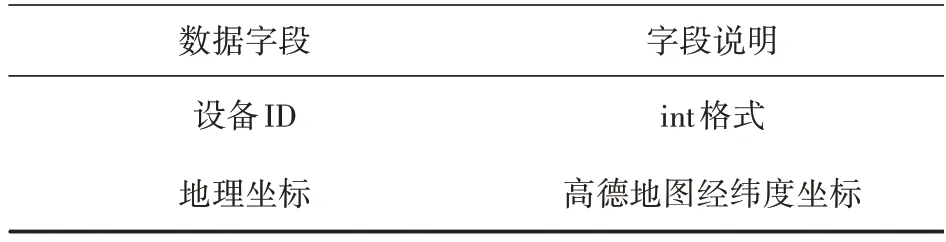
表1 （续）

冬季我国不同地区的道路结冰特点并不一致。北方地区冬季干燥、气温低，因此湿度成为结冰的关键因素；南方地区湿度大，路面气温是结冰的关键因素。本文以我国南方地区和北方地区多个监测点：青岛胶州湾大桥、山东青兰高速、内蒙古G6 高速、兰州西固黄河大桥、南京宁杭高速、贵州观风海大桥等安装的路面传感器近5 年采集的路面气象数据作为依据，进行神经网络模型训练和验证。

1.2 异常数据处理

传感器采集数据后上传至系统存储的过程中，存在系统存储故障、数据传输失败、数据传输异常等现象，从而导致原始数据中可能存在噪声数据[12]。如果直接使用会造成计算结果偏差，因此需对原始数据进行预处理。本文主要采用剔除异常数据和均值插值的方法处理噪声数据。

根据路面结冰时的数据采集时间，取出前5h之内该采集点的数据，对异常数据进行筛查。由于传感器数据为时间序列变量，故以特征值某时点前后10min 的平均值作为基准数据，计算该时点数据与均值的偏差，偏差大于均值0.5 倍的数据会被剔除，然后采用均值插值。导致异常数据的原因主要有：采集数据缺失、路面状态数据不准确、路面温度变化异常。

（1）数据采集存在明显缺失

传感器每5min采集一次数据，当发现数据存在某段时间范围内缺失或存储时间不连续的情况，如图2 中，从19:20 开始到19:50 存在数据缺失的情况，则需对该样本数据进行处理。

（2）路面状态数据不准确

根据路面传感器采集的数据，路面状态在一段时间内应该为干燥、潮湿、结冰、积雪中的一种，如果存在频繁变化的情况，即认为该段时间的路面状态数据不准确，可将此类数据剔除。

（3）路面温度变化异常

路面温度会随着时间变化而变化，通常情况下中午路面温度要比早晚温度高，基本趋于线性变化的趋势。如果某段时间温度有忽上忽下的大范围波动，可认为该段数据异常。如图3 所示，19:40 和20:10 有两次明显的数据抖动，需进行均值插值处理。

1.3 数据相关性处理

通过对数据进行筛选，选取50个监测点2016—2022 年的数据，对数据进行统一分析处理。本文对数据的处理分两步进行：第一步，进行特征选择，剔除强相关的数据项，减少数据维度，为以后的神经网络训练降低计算复杂度，减少模型的训练时间；第二步，进行归一化处理，使用min-max 标准化方法，提升模型的收敛速度和精度。

采用过滤法（Filter）中的相关系数法进行特征选择，本文采用Pearson相关系数法，该方法具有消减误差比例的作用，是认可度最高的用于刻画变量相关性系数的方法。Pearson 计算公式如下[13]:

式（1）中：r为相关系数；Xi,Yi为计算相关性的两个样本点，为样本的平均值。计算8 个变量间的相关系数，见表2 。从表2 中可知，含盐量与冰点温度的Pearson 相关系数r为-0.951，故这两项数据为强相关。

表2 数据项间相关系数计算结果

经Pearson相关性系数计算后，再对冰点温度和含盐量做散点图进一步验证其相关性（见图4）。从图4 可知，含盐量与冰点温度呈线性关系，进一步验证了其强相关性，故舍弃冰点温度这一特征，以降低神经网络的复杂度，减少训练时间。

1.4 数据归一化

将BP 神经网络算法应用于凝冰预警中，需将凝冰数据作为算法输入项。根据神经网络算法的特点，若将其直接输入网络，则加权后通过累加，各种数据间的差别将变得非常大，从而导致网络难以收敛。因此，为消除数据属性值之间的差别，平滑数据样本值，需对输入的凝冰数据进行归一化处理。目前主要使用min-max 标准化法，将数据按比例缩放，使之落入一个小的特定区间，如果直接用原始指标值进行分析，就会突出数值较高的指标在神经网络模型中的作用，而削弱特征值水平较低指标的作用，因此将凝冰数据转化为无量纲的纯数值，便于不同单位量级的指标进行比较和加权。本文使用min-max 标准化法[9]对原始数据进行线性变换，使自变量映射到(0,1)之间，转换公式如下：

式（2）中：x'为变换后的数据；x为样本数据；xmin为样本集最小值；xmax为样本集最大值。以2022 年1 月17 日采集的一段结冰前的数据为例，路面初始数据和归一化后数据如表3所示。

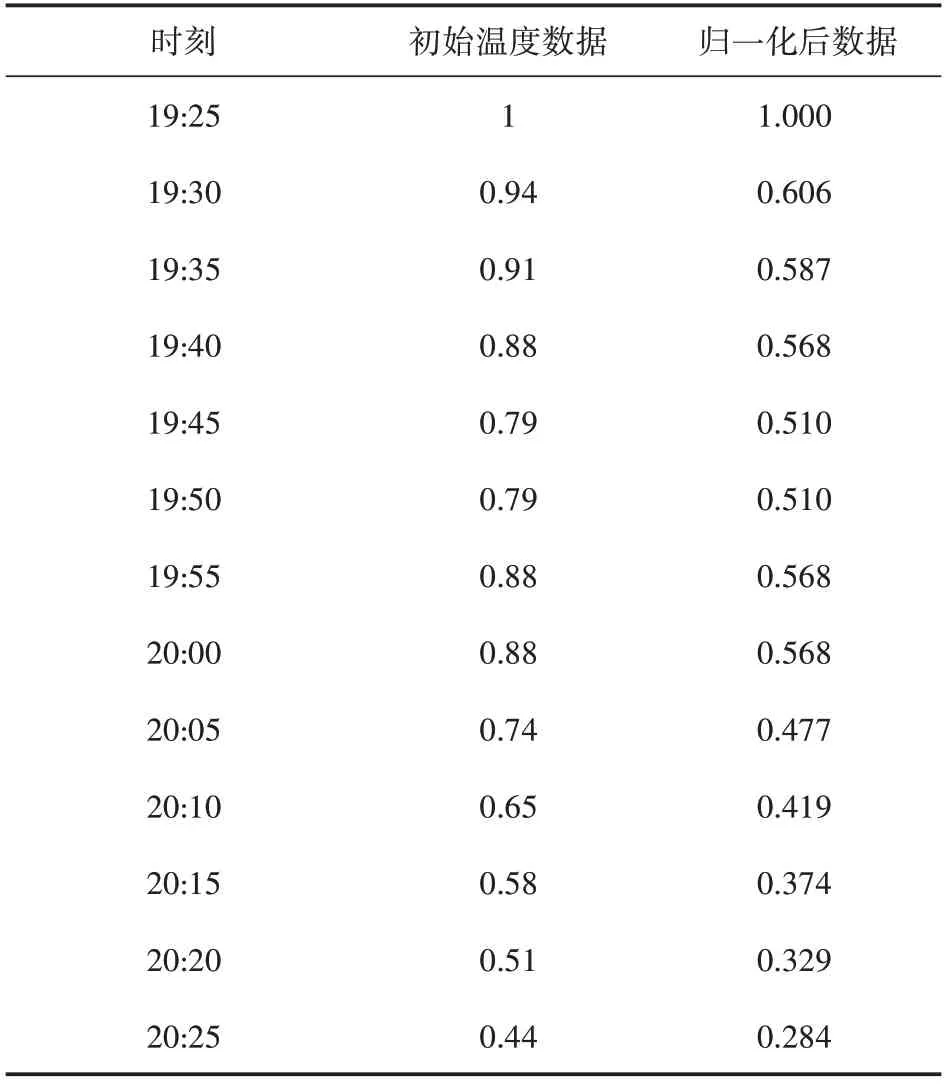
表3 路面温度归一化处理后数据

2 预测模型构建

2.1 算法基本思想

本文采用BP 神经网络算法，其原理是输入学习样本，通过反向传播算法对网络的偏差和权值进行反复训练，使最终得到的输出值尽可能与期望值接近。首先构建神经网络，设置输入层和输出层的数量，然后根据凝冰数据的特点选择合理的激活函数和防止过拟合的方法，最后进行模型训练。训练数据选取2016—2022 年山东、内蒙古、贵州等多地30 个监测点的路面、气象数据。该数据通过气象站和路面传感器每分钟采集一次后存储在云服务器中，包含本文第1 小节所列出的所有路面凝冰数据。

2.1.1 模型构建

模型构建第一步是确定神经网络的拓扑结构。BP神经网络包含三层：输入层、隐藏层、输出层。据上节可知本文凝冰特征变量有6 类，且都为时序变量，故选取tn-6,tn-5,tn-4,…,tn时刻的所有特征值作为输入层，输出层为距离凝冰的时间Y，则输入层为36×1，输出层为1×1。神经网络结构如图5所示。

建立模型时无法确定模型隐藏层的层数以及每层的神经元数，为此，采用网格搜索法（如图6 所示），在所有候选的参数中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的选择结果。

2.1.2 激活函数选择

目前激活函数的种类主要有Sigmoid、Tanh、Relu等[14]。Sigmoid 函数是将取值为(-∞,+∞)的数值映射到(0,1)之间。Sigmoid函数如下：

式（3）中：z为需要映射的值。

Sigmoid饱和区域较广，容易出现梯度消失的问题。通过式（4）可知，当z非常大时，会导致该节点权重g(z)的梯度将接近于0，使得梯度更新十分缓慢，即梯度消失。

式（4）中：g'(z)为g(z)的求导，表示g(z)的梯度。

Tanh 函数相较于Sigmoid 函数要常见一些，该函数是将取值为(-∞,+∞)的数映射到(-1,1)之间，其公式如下：

Tanh 函数在0 附近很短一段区域内可看作为线性。由于Tanh 函数均值为0，因此弥补了Sigmoid 函数均值为0.5 的缺点，但是Tanh 函数和Sigmoid 一样也容易出现梯度消失问题。当z很大或很小时，g'(z)接近于0，如式（6）所示，会导致梯度很小，权重更新非常缓慢，出现梯度消失问题。

Relu 是一种分段线性函数，弥补了Sigmoid函数以及Tanh函数的梯度消失问题。Relu函数的表达式如下：

式（7）中：x为样本值。

Relu 没有饱和区，不存在梯度消失问题（如图7 所示）。

本文的数据多为正数，只有路面温度可能为负数，输入为正数的时候，不存在梯度消失问题。Relu 函数只有线性关系，计算简单，而Sigmod 和Tanh要计算指数，计算速度较慢，因此Relu函数不管是前向传播还是反向传播，都比Sigmod 和Tanh快，故本文选择使用Relu为激活函数。

2.1.3 防止过拟合

为防止模型训练中的过拟合现象，本文采用在每一个全连接层后添加批归一化BN(Batch Normalization)层或Dropout 层，或者在损失函数中添加正则化项等方法[15]。

Dropout通过在前向传播时，让某些神经元停止工作（如图8所示），可以减少过拟合、提升模型的泛化能力。

2.2 神经网络模型的训练过程

如上所述，完成模型输入输出、激活函数选择和防止过拟合等构建工作后，本节对神经网络模型进行训练，过程如下：

第一步：数据集划分。本文将数据集按9∶1划分为训练集和验证集。为防止模型训练中的过拟合现象，采用在每一个全连接层后添加BN 层或Dropout 层，以及在Loss 函数中添加正则化项两种方法。

第二步：前向传播后计算输出值y和真实值z之间的误差δ=z-y，用误差反向传递给前面的各层来调整网络的参数，如图9所示。

将要传播的误差δ返回分配给所有神经元，从而得到每个神经元的各自误差δ5,δ4,…,δ1（如图10所示）。

每个神经元的误差都计算完后，其权重也会更新，如图11展示了4号神经元的更新过程。

向前传播更新权重的计算公式如下：

式（8）：W46为上次的旧权重；为更新后的权重；η为学习率；为误差梯度。训练过程为：首先通过误差反向传播，获得每个神经元的误差值，再根据误差值和激活函数的导数来更新权重，最终达到对整个网络的修正。

第三步：模型训练。采用交叉验证法，一个单独的子样本被保留作为验证模型的数据，其他K-1 个样本用来训练。交叉验证重复K次，每个子样本验证一次，平均K次的结果或使用其他结合方式，最终得到一个单一估测集。交叉验证法的优势在于同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10 折交叉验证是最常用的[16]。

训练集采用K折交叉验证法，将数据集按9∶1 划分为训练集和测试集，轮流将其中9 份作训练数据，将剩下的1 份作测试数据，10 次结果的均值作为对算法精度的估计。K折交叉验证法如图12所示。

第一个训练集进行训练得到的结果如图13所示。从图13 中可以看出，在距离结冰120min 内测试的30 组数据中，第0～5 和18～22 的数据区间预测值和实际值偏差较大。由于第一次训练学习的数据比较少，模型的成熟度不够，所以预测值与实际值差别比较大。

根据第一组的建模预测结果调整神经网络内部各节点权值，继续进行其余几组数据的模型训练。10 组全部训练完毕后，将所有数据进行乱序，检测模型的准确度。经10组数据训练完毕后对预测结果进行对比（如图14 所示）。预测结果在120min 内接近实际值，趋势和真实结果基本吻合。

3 预测模型验证

3.1 评价标准

采用平均绝对误差（Mean Absolute Error,MAE）、均方误差（Mean Square Error,MSE）两项评价指标对预测模型精度进行对比分析。平均绝对误差是目标值与预测值之差绝对值的平均，表示预测值的平均误差幅度，而不需要考虑误差的方向。本文预测结冰的时间比实际结冰时间或大或小，综合考虑时间的差距，使用MAE能反映预测时间的偏差程度。MAE计算方法如下：

式（9）中：h(xi)为预测的距离结冰的时间；yi为实际值；m为计算的数据集个数。

MSE 是反映估计量与被估计量之间差异程度的一种度量。t为根据算法预测的凝冰时间值，θ是实际凝冰时间值，(θ-t)2的数学期望称为预测值t的均方误差。MSE 能反映预测结冰时间与实际结冰时间之间的差异程度，差异越小越好，其计算方法如下：

3.2 案例验证

为验证模型的预测效果，本文使用预测模型对全国30 个监测站2019—2022 年的结冰时间进行了预测，并对预测结果进行对比分析和数据可视化。

使用贵州观风海大桥2022年1月17日路面传感器监测到的路面结冰时间数据，将预测时间与实际结冰时间对比，如图15 所示。从图15 可以看出，系统预测的时间在120min 前呈波动的状态，与实际数据相差较大。该监测站点当天19:25—22:25 的监测数据如表4 所示，因采集数据量很大，本文中只展示每5min 的数据。从表4 中可以看出，该监测点22:25 产生结冰现象。在结冰前3h 即19:25—20:25 的时间段中，也就是预测时间相对不准确的范围内，温度在19:40—20:00 有多次下降、上升的情况。温度上升意味着结冰的可能性减小，所以模型对该段时间的预测产生了偏差，结冰前120～180min的预测数据存在波动且与实际不符。随着20:25 后各项数据表明趋向结冰状态越来明确，模型调整了自己的预测时间并和实际结冰时间越来越吻合，结冰前0.5h 内预测时间基本与实际时间一致。由表4 可知，21:10 时温度已经下降到0℃以下，路面存在积水（水膜厚度为199.7μm），已经到达结冰条件，但需要一定的时间才会有一定量的冰产生。1h 后，22:25 路面传感器检测到了结冰。本文的模型训练过程中都是以路面传感器第一次监测到路面有冰的状态为路面结冰时间，而不是以路面温度下降到0℃为结冰时间点。

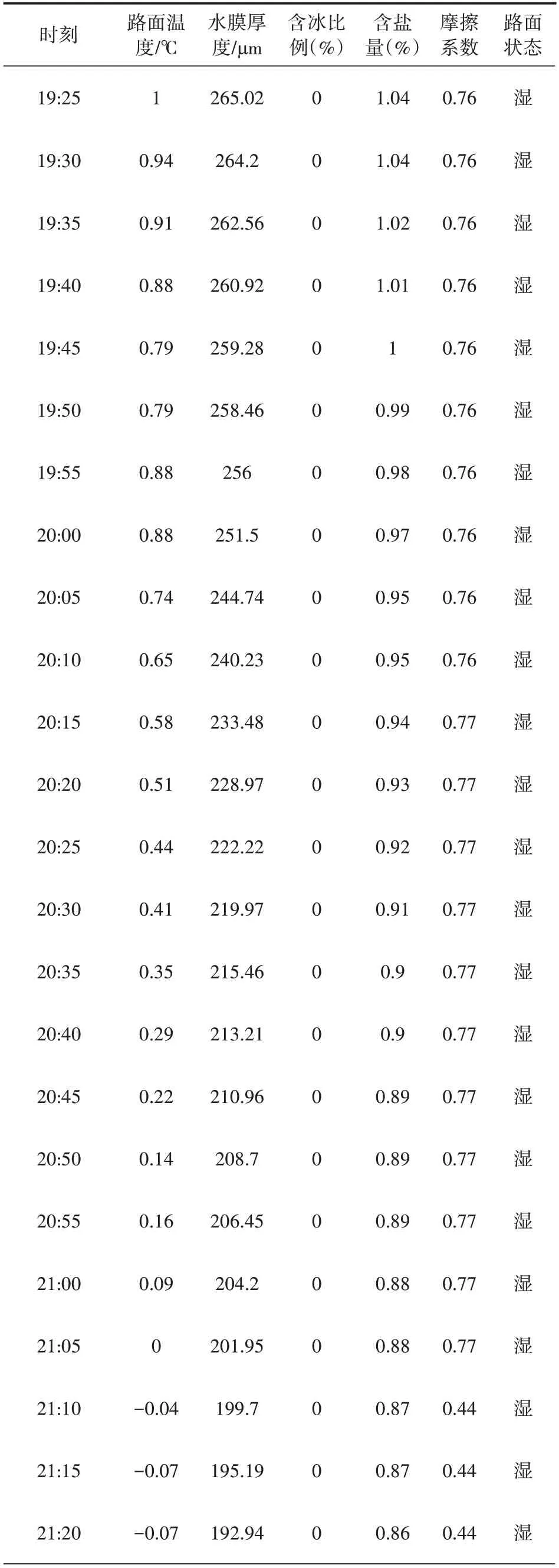
表4 贵州观风海大桥路面状态变化情况（2022年1月17日）

表4 （续）

对所有结冰数据进行验证，经计算平均绝对误差（MAE）为9min，均方误差（MSE）为174。并且2h之内预测模型对越接近结冰点的时间预测越准确，从统计结果可看出60min 之内的预测数据和实际数据几乎完全一致，说明神经网络计算模型对结冰前2h内的时间预测较准确，能反映出结冰时延。

4 结语

本文提出了使用神经网络进行道路结冰时间预测的方法，以胶州湾大桥、青兰高速、内蒙古G6 等数个监测点5 年的道路气象数据作为数据集进行预测模型训练和验证。首先选取结冰前一段时间的数据进行预处理并剔除相关性较强的特征数据，然后基于BP 神经网络算法构建结冰预测模型，使用数据集进行模型训练，经过训练后对模型进行验证。验证结果表明距离结冰2h内的预测平均误差为9min，使用BP 神经网络算法能较准确预测距离结冰的时间。该方法丰富了目前预测结冰时延的手段，能为高速公路养护部门提前采取除冰措施提供参考。但因目前采集的路面传感器数据只有近5 年的数据，如果能使用更大量的数据和更丰富的数据种类，预测的精准度将更高。本文在模型计算过程使用的激活函数和防止过拟合方法较单一，没有对其他方法进行试验，尚未考虑使用其他方法对准确性的影响，有待进一步深入研究。