基于雷达与相机融合的行人轨迹跟踪
2022-10-17李宏晖张昊宇
李宏晖,张昊宇
(1.浙江海洋大学 海洋工程装备学院,浙江 舟山 316000; 2.浙江海洋大学 信息工程学院,浙江 舟山 316000)
0 引 言
目前,大多数实时多目标跟踪算法是基于相机传感器设计的,但相机在一帧中可以捕捉到的像素数量是固定的,目标与传感器之间的距离会对跟踪精度产生很大的影响。事实上,代表同一目标的像素量将随着传感器和目标之间距离的增加而呈平方递减。然而,毫米波雷达能够通过目标与雷达的距离信息来区分不同的目标,且毫米波雷达的一个重要优势是不易受环境条件的影响,如雨、灰尘、烟雾、雾或霜[1]。但与激光雷达相比,毫米波雷达角分辨率太低。激光雷达分辨率高、抗干扰能力强,但也存在数据交换量大, 软、硬件成本高等问题。
基于上述原因,研究人员开始探索异类传感器融合在目标跟踪领域的应用。Heuer等使用24 GHz雷达和先跟踪后探测的方法来实现目标跟踪。他们的方法是基于一个粒子滤波器[2],其权重受人体行走引起的多普勒信号的影响。但该系统仅限于跟踪单个目标,而不考虑轨迹的创建和终止等事件。Gruyer等提出了一种基于激光雷达和相机的融合方法。但该方法不执行任何类型的对象分类,并且依赖基于检测区域大小和运动模型的假设。Yenkanchi等[3]提出了一种基于雷达和相机的协同测距成像探测器,用于道路障碍物检测。作者使用试探法将矩形遮罩应用于各种对象,如汽车、卡车、行人等。得到的图像遮罩在视觉上与图像内容相匹配。然而,还不清楚这些遮罩如何用于对特定目标进行分类,以及是否有性能改进。
综合考虑上述方法出现的问题,本文设计了一种先检测后跟踪的算法。基于Felix等[4]的研究,利用CRFNet神经网络代替传统纯图像网络对目标进行检测。借鉴Martin等[5]和Alessio等论文中描述的结构,采取在特征层对雷达数据与图像进行融合的方法,并受到Michael等[6]工作的启发,通过粒子滤波算法处理这些融合信息最终实现对行人多目标的精确跟踪。
1 算法流程图
本文的跟踪算法采用先检测后跟踪的工作模式,先借助CRFNet神经网络对图片进行检测得到目标边界框,再根据针孔模型估计目标在地平面上的位置坐标。接着利用目标的位置坐标对雷达点云进行修正与筛选,并根据处理后得到的点云数据设计了一种改进的粒子滤波算法。算法流程如图1所示。
2 基于传感器融合的目标检测
2.1 雷达点云与图像融合
本文所使用的CRFNet网络通过对图像和雷达信号进行融合以提高网络的目标检测性能,其融合方法如下。
雷达传感器的输出包括三维点云和相关的目标参数,如速度、信号强度等。考虑到雷达点云的高度并不能反映物体的实际高度,所以首先将雷达点云高度置为0,然后将雷达数据从三维空间中映射到图像平面。根据欧盟的数据,人类的平均身高为1.7 m,因此我们将雷达投影由投影点向上、下延伸为1.8 m长的线段,使雷达投影尽可能完全覆盖行人目标。
雷达点云的投影以像素值的形式存储在融合图像中。在无雷达回波的图像像素位置,将投影雷达通道值置为0。图像由红、绿、蓝3个通道组成,在此基础上,我们将雷达通道与图像通道相连作为神经网络的输入,如图2所示。
分别对毫米波雷达与相机进行空间标定,得到旋转矩阵R与平移矩阵T。再通过张正友标定法对相机进行内参标定,得到图像空间坐标系到像素坐标系的转换矩阵。最后将投影以投影点为中心,往竖直方向上、下分别延伸0.9 m,生成一个1.8 m长的竖线。图3(a)为雷达测得的三维点云图,图3(b)为将点云投影到图片上的效果图。
2.2 基于传感器融合的神经网络架构
CRFNet(如图4所示)神经网络架构建立在RetinaNet[7]上,并以VGG16为基础网络。网络的输出端分别为边界框回归子网络和目标分类子网络。如文献[7]中所建议的,网络使用聚焦损失(focal loss)作为目标分类的损失函数,并使用smooth L1作为边界框回归的损失函数。
融合网络的主干为图4中特征提取子网络的第二列,由VGG16模块组成。相机数据流和雷达数据流通过连接器连接,并在第一层输入VGG16的模块1。网络的这一分支通过VGG16层处理相机和雷达的融合数据。在左边的分支中,原始雷达数据通过最大池化以相应的比例输入到网络的更深层,同时与VGG16层的输出相连接。
接下来再在输出端引入特征金字塔网络(FPN)[8]由模块P3到P7表示,通过在每个级别上的级联来额外地融合雷达通道。FPN模块的输出连接了两个子网络,分别是边界框回归子网络和目标分类子网络。
2.3 数据关联与针孔模型
借助CRFNet网络检测到行人目标后,需进行以下两步操作,为后续粒子滤波算法提供必要数据:一是借助KM算法实现前、后帧目标的数据关联,并得到目标a、b之间的色差Cola,b; 二是借助针孔模型计算行人在地平面上的位置坐标。
(1)根据匈牙利算法的改进算法KM算法对相机前、后帧检测出的目标进行关联。KM算法即是在一个二分图内,每一组左右连接有权值ωab, 求一种匹配使得所有ωab的和最小。本实验中,设定ωab为前一帧目标a与后一帧目标b之间的颜色差值Cola,b。 为了减小背景对算法的干扰,取目标边界框的中间部分(水平方向为[1/3,2/3],竖直方向为[1/5,7/10])作为目标的颜色取样区间。分别对目标a、b的颜色取样区间中的所有像素的红(r)、绿(g)、蓝(b)这3个颜色通道取平均值 [ra,ga,ba]、 [rb,gb,bb], 且已知每个像素的通道颜色的取值范围为1~256。Cola,b如式(1)所示
(1)
(2)“针孔模型”首先为目标的实际高度设置一个估计值H,再借助目标边界框的位置和大小来估计目标在地平面上的位置坐标。
针孔模型如图5所示,通过一个代表相机镜头的点,将三维世界映射到图像平面。其中,左部分人像表示行人在图片平面上的投影,右部分表示人在三维空间的位置。f表示相机焦距,D表示行人的中心位置到相机的距离,h表示目标边界框的宽度,H表示行人身高的估计值,d表示目标边界框中心到相机镜头的距离,c表示边界框中心到相机镜头在图片上垂直投影的距离,F表示行人到相机的距离。边界框中心点在图像平面上的位置可表示为 (px,py)。 则行人在地平面上的位置坐标 (x,y) 为
(2)
(x,y)=(D·sin(θx),D·cos(θx))
(3)
3 基于传感器融合的粒子滤波
3.1 传感器误差
本节对相机传感器与雷达传感器的测量误差做简要介绍,为后续雷达点云的预处理提供必要参数。
(1)目标距离误差:
借助针孔模型可以得到行人在地平面上的位置,但其中有两步操作会产生误差:①用目标边界框的高度h来近似行人在图片中的高度;②在针孔模型中将行人的身高统一假设为H。经过多次实验发现第一类误差很小可忽略不计。针对第二类误差,先假设行人真实身高为γH, 如图6所示。
再由针孔模型可得
f=dcos(θx)
(4)
(5)
根据欧盟的数据人类的平均身高为1.7 m,因此本文设定H=1.7m。考虑到多数行人的身高区间为[1.5m,1.9m],根据公式可得目标距离误差ΔD最大为d/5hm。
(2)雷达点云的切向误差:
根据本实验所使用毫米波雷达的参数说明书,本款雷达的角分辨率为1.4°,因此雷达点云点相对于雷达的切向误差最大约为1/40Dm。
3.2 雷达点云预处理
本文设计的粒子滤波算法使用雷达点云的相关参数对粒子的权值进行更新。雷达点云含有大量噪声,本文设计了一种算法,借助上一节介绍的参数对雷达点云进行校正、筛选。
相机传感器具有很好的角度分辨率,但距离分辨率较差。而雷达传感器正好相反,距离分辨率优良角度分辨率较差。为融合二者优点本文采取以下融合方法:
(1)借助针孔模型得到行人位置坐标。
(2)(考虑到相机有很高的角分辨率,因此本文以相机检测到的目标方位角作为基准,对雷达点云进行筛选)以相机为坐标原点,向行人位置坐标射出一条射线。
(3)由前文可知目标距离误差最大为d/5hm, 雷达点云切向误差最大为1/40Dm。因此以预估的目标位置为中心建立一个长为2d/5hm、宽为1/20Dm的方框作为采样区间,并将方框所覆盖的点云点映射到第2步确定的射线上(点云点与雷达的距离保持不变),其余的点云点丢弃。
(4)将第3步所得的点云点作为本次迭代的观测值。以上操作如图7所示。
3.3 从运动模型采样
粒子滤波分为3步:采样、权值更新、重采样。
假设粒子在每次检测间隔ΔT内速度恒定,即粒子速度等于粒子在ΔT内运动的距离除以ΔT。然而这种运动模型存在误差,因此引入高斯噪声εi。εi的协方差定义如式(8)所示,这样设计有两个原因:①基于恒速假设得到的速度与实际速度有误差,可以借助参数α进行部分补偿;②粒子有加速度,所以检测间隔ΔT越短,误差越小。
εi的均值为粒子以当前速度在ΔT内的运动距离。定义了所有参数后,位置预测公式如下

(6)
(7)
(8)
3.4 通过观测模型修正粒子的权值
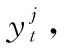
(9)
μj=[xj,yj]
(10)
(11)
其中,M表示当前雷达点云的点的个数。μj=[xj,yj] 表示当前帧第j个点云点的坐标。Ij为第j个点云点的信号强度。Cola,b为不同目标间的颜色差值。参数δ=28。
4 实验结果和分析
4.1 实验设备和参数
本实验使用的设备是TI公司的MMWCAS-RF-EVM 4D毫米波雷达,该款雷达由4块AWR2243毫米波雷达芯片级联而成,具有高穿透特性、高信噪比和高角分辨率的特点。其拥有192个信道是普通毫米波雷达的16倍,并且可在140°水平、60°纵向的宽视场中提供0.8°水平、1.4°纵向的角分辨率。雷达的优异性能大大提高了本文算法的跟踪精度。此外,该款雷达能探测距离超过350 m的大型物体(例如汽车和卡车),距离分辨率为35 cm;人体RCS可探测物体能在150 m的距离内被探测到。雷达有波束成形和MIMO两种工作模式,本实验主要在MIMO模式下进行。
本实验使用的视觉传感器型号为PointGrey Blackfly S USB3.0,采集分辨率为2048×2048像素,RGB模式下帧频率为25帧/s。
本实验控制平台配置如下:Intel(R)Core(TM)i5-10210U CPU@1.60 GHz,16 G内存,Ubuntu 16.04操作系统。目标检测程序运行环境如下:Python版本为3.5,Anaconda版本为4.2.0。训练神经网络选用的数据集为nuscenes[9]。粒子滤波程序运行环境为matlab。
4.2 参数优化
对式(8)中的参数α和式(11)中的参数δ进行优化。取滤波的结果与真实运动轨迹的均方根误差(RMSE)作为评价标准,RMSE反映了滤波器粒子在跟踪过程中偏离真实轨迹的程度。
为了平衡不同运动场景对参数的影响,为参数优化选取4个典型运动场景:①单个行人做直线运动;②单个行人做圆周运动;③两个行人做十字交叉运动;④两个行人做相向运动。为了防止过拟合,将4个测试场景中得到的4个RMSE的平均值作为最终值。
经过多次测试,发现当α被设置为大于4的值时,粒子不会收敛到任何目标上,因此设置α测试区间为[0,4],结果如图8(a)所示。观察图8(a)发现当α设置为较小的值时能得到更好的结果,因此修改测试区间为[0,0.5]再次进行实验。
在实验场地测试得到的雷达信号强度的变化范围为[20,50],所以设置δ的测试区间为[1,100],使得测试的标准偏差区间为[0.14 m,2.24 m]在可接受范围内。
最终实验结果如图8(b)、图8(c)所示,可得当α=0.1、δ=28时对应的均方根误差最小。
4.3 算法测试结果与对比

为验证本文算法在行人目标被遮挡情况下的检测性能,在实验场地对算法进行测试,并与Martin[10]开发的最新的融合算法结果作对比。此外,为提高测试样本多样性,选取nuscenes数据集中存在行人目标被遮挡情况的样本集进行测试。考虑到雷达采样频率为10帧/s,相机采样频率为25帧/s,本实验首先通过时间配准将雷达和相机的采样频率同步为10帧/s。单次实验的雷达采样数设置为400帧,粒子滤波器的粒子总数设置为5000。测试结果如下:
图9~图12为4种不同场景中行人目标被遮挡情况下的测试结果,其中每幅图的图(a)、图(c)为Martin算法的检测和跟踪结果,图(b)、图(d)为本文算法的检测和跟踪结果。图9为室内场景中的测试结果对比,可以看到图9(a)中被部分遮挡的目标没有被检测出来,导致图9(c)中的跟踪轨迹出现了明显的间断,并且当被遮挡的目标再次被检测到时,Martin算法将其错误判断成新出现的目标。从图9(b)、图9(d)中可发现本文设计的跟踪算法能在目标被部分遮挡时,仍然对目标精确跟踪。图10为道路场景中的测试结果对比,可以发现Martin算法错误的将3个距离很近的目标识别为同一目标,而本文的算法能够准确区分每个目标。图11为夜间场景中的测试结果对比,可以发现相机传感器几乎看不到两个行人,因此仅通过图像无法检测到他们,但基于融合数据的网络能够检测到它们。图12为雨天场景中的测试结果对比,与夜晚的场景类似两个行人只能被雷达探测到,Martin算法只能在目标距离较近时正确检测,当目标距离较远时跟踪失败,但本文算法始终能成功检测并跟踪目标。
为了进一步验证本文算法的优势,采取对照实验,将本文提出的跟踪算法分别与Martin等[10]、吴宪等[11]、刘志强等[12]开发的融合算法进行对比。在实验场地通过改变行人的个数和行人与传感器的距离进行了多组实验,实验包括4种运动模式:①实验1和实验2为单个行人做圆周运动;②实验3和实验4为两个行人做十字交叉运动;③实验5和实验6为3个行人做“川”字运动,其中最外围的两个行人与中间行人的运动方向相反;④实验7和实验8为4个行人做“丰”字运动,其中横向运动的三人各自的运动方向与相邻的行人相反。对比跟踪结果与真实运动轨迹的均方根误差(RMSE)得到表1。我们发现虽然4种方法的跟踪精度都随距离的增加而降低,但本文算法的平均RMSE达到了1.2 m,相比之下,Martin跟踪算法的平均RMSE为1.38 m,吴的为1.33 m,刘的为1.39 m。显然,本文提出的融合算法对目标的跟踪效果更精确,RMSE提高了超过10%。相较于其它算法,本文的算法使用CRFNet作为检测网络,大大降低了光线等外部条件对算法的干扰,提高了跟踪精度。此外,本文的融合算法借助相机测量结果对点云数据进行了矫正,并能够在相机丢失目标时利用雷达点云继续对目标进行跟踪,最终使精度提高了约10%。
最后对本文、Martin、吴和刘的算法在时间延迟和丢失率上进行了定量比较,结果见表2。刘的算法相比于Martin、吴的算法在时间延迟方面有了很大改善,但在丢失率方面改进不大。本文算法相比于Martin、吴和刘的算法在目标丢失率方面大大改善,并将时间延迟缩短至4 ms,满足了系统对实时性的要求。
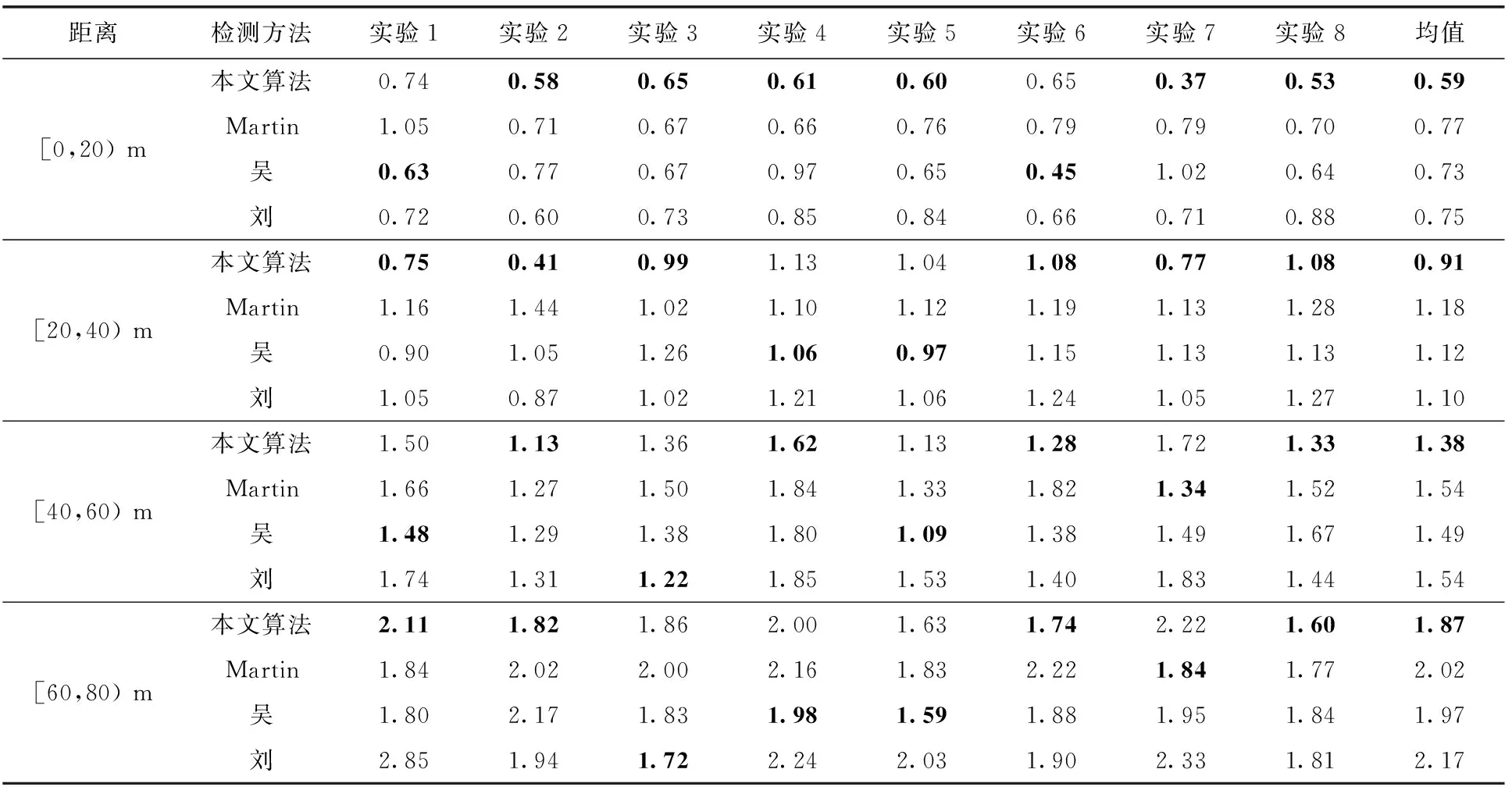
表1 对照实验的均方根误差

表2 各检测方法性能对比
5 结束语
本文利用CRFNet神经网络对相机和雷达信号进行融合,提高了算法在复杂光线与恶劣气候条件下的跟踪精度,增强了系统的鲁棒性。设计了一种基于针孔模型与传感器误差参数的融合算法,大大降低了雷达噪声与传感器误差对跟踪结果的影响。此外,本文还设计了一种改进的粒子滤波算法,在相机丢失目标时仍能借助雷达数据继续跟踪目标。
与传统融合跟踪算法相比精度上提高了10%,并一定程度上解决了Martin等融合跟踪算法在目标被遮挡情况下易跟踪失败的问题。
