考虑低资源损耗的云平台虚拟机放置策略
2022-10-17李少旭李雷孝王永生
李少旭,李雷孝+,邓 丹,林 浩,高 静,王永生
(1.内蒙古工业大学 数据科学与应用学院,内蒙古 呼和浩特 010080;2.内蒙古自治区科学技术厅 内蒙古自治区基于大数据的软件服务工程技术研究中心,内蒙古 呼和浩特 010080; 3.内蒙古农业大学 计算机与信息工程学院,内蒙古 呼和浩特 010011)
0 引 言
云计算作为继分布式计算、并行计算、网格计算以来新的计算模式,以其成本低廉、安全可靠、可按需分配的资源池机制的特点,已经在全球范围内得到了快速发展[1]。随着云数据中心的规模不断扩大,资源损耗严重与低利用率的问题日益突出[2-4]。虚拟机迁移机制是云平台提高资源利用率、降低能耗的重要手段。虚拟机放置是虚拟机迁移的一个重要环节,虚拟机放置位置的优劣影响着数据中心的资源分配状况[5]。如果数据中心资源损耗严重,必然需要开启更多的物理机来放置虚拟机。这将会造成资源浪费、增加运营成本[6]。
本文以最小化资源损耗为优化目标,以物理机上可用的CPU、内存、网络带宽和磁盘资源作为约束条件构建了虚拟机放置模型。在模拟放置阶段将虚拟机放置问题转化为多维装箱问题,结合粒子群算法(particle swarm optimization,PSO)解决最优化问题的思想方法,提出一种基于正余弦扰动和反向学习的自适应粒子群算法(based on sine and cosine perturbation and reverse learning adaptive particle swarm optimization,SCRLPSO)的虚拟机放置策略。首先对数据中心资源结构进行分析,建立最小化资源损耗目标的虚拟机放置模型;然后对物理机和虚拟机的映射关系进行编码,使用反向学习策略进行种群初始化。在种群寻优的过程中,通过正余弦扰动避免种群陷入局部最优解,使用开口向下的权重更新策略增强种群的全局搜索能力。实验结果表明,和标准的粒子群算法、传统的首次适应法、最佳适应法相比,基于SCRLPSO算法的虚拟机放置策略更能降低数据中心的资源损耗程度。
1 相关工作
解决虚拟机放置问题的传统方案是基于贪婪思想的启发式算法,如首次适应法(first fit,FF)[7]、最佳适应法(best fit,BF)[8]等,目的是尽可能减少数据中心处于活动状态的物理机的数量来减少能耗,提高资源利用率。但是这种基于贪婪思想的虚拟机放置策略在异构集群中可能会导致某些物理机负载过高,这会导致运行在其上的虚拟机服务质量的降低。而有些物理机可能会处于低载状态,物理机资源没有得到充分利用。因此这种基于贪婪思想的虚拟机放置策略可能会导致负载失衡。
近年来,一些基于机器学习的方法被用于求解虚拟机放置问题。卢海峰等[9]提出了一种强化学习下的虚拟机放置策略,该策略以能耗为优化目标,从状态聚合和时间信度两个方面对Q-Learning(λ)算法进行优化,可以有效降低数据中心的能耗。郭曙杰等[10]提出一种基于模糊隶属度的虚拟机放置策略,借助模糊聚类的思想,计算虚拟机与物理机的隶属度矩阵,在矩阵中局部搜索得到最优的放置方案。
元启发式算法也广泛应用于虚拟机放置问题。何利文等[11]提出了一种基于权值适应度粒子群优化算法,以通讯时延、服务器负载以及CPU的处理时延作为虚拟机放置的依据,对PSO算法的权重因子ω重新编写,能更好地降低应用的执行时间。Gharehpasha等[12]提出一种混合正弦余弦算法和樽海鞘群算法的虚拟机放置策略,该策略通过最小化活动物理机的数量来降低能耗。Ragmani等[13]提出一种用于虚拟机调度的混合模糊蚁群优化算法,以响应时间、处理时间和负载均衡为优化目标,根据历史信息计算信息素值,为虚拟机选择合适的物理机。
传统的PSO算法存在容易陷入局部最优解、收敛速度慢等缺点。目前国内外很多专家学者在改进PSO算法上做了相关的研究工作。宁维迪[14]针对粒子群算法容易陷入局部最优解的不足,将正弦余弦算法应用于粒子群算法的学习率更新,使粒子群算法具有较好的全局搜索能力。张继荣等[15]将正弦余弦策略应用于粒子群算法权重更新中,使算法在运行初期具有良好的全局搜索能力,后期快速逼近全局最优解。张志宇[16]对粒子群算法提出改进,使用三角函数来调整粒子群算法的权重,使用指数变化的学习因子来调整粒子向自身学习和向种群学习的能力,在算法运行前期快速搜索到局部最优解,在后期加强全局搜索能力,向全局最优解靠近。
上述对虚拟机放置问题的研究缺乏对资源损耗和服务等级(service level agreement,SLA)的权衡,同时考虑上述对PSO算法改进策略,本文提出一种基于正余弦扰动和反向学习的自适应粒子群算法的虚拟机放置策略。在尽可能降低云平台资源损耗的同时,保障用户的服务质量。
2 虚拟机放置的约束优化目标模型
2.1 数据中心模型描述
数据中心是支撑云服务的基础环境,其通过对大量闲置的计算机系统资源进行虚拟化,构成一个可以按需分配、动态扩展的虚拟资源池。虚拟机是数据中心对用户进行资源分配的基本单位。虚拟机放置问题[17],是指按照一定的放置策略,在满足资源约束的情况下,为虚拟机选择一个合适的物理宿主机,从而达到减少资源损耗、节约运营成本、提高运行效率等目的。
图1描述了用户向数据中心提出资源请求,数据中心将资源请求分配到物理机上的工作场景。s个用户向数据中心请求创建n台异构的虚拟机 {vmi,i=1,2,…,n}, 数据中心现有m台物理机 {pmj,j=1,2,…,m}, 要将这些虚拟机合理地放置在m台物理机上。一台物理机能够放置多台虚拟机,而一台虚拟机只能被放置在一台物理机上。
数据中心提供的物理资源主要包括CPU、内存、网络带宽、磁盘。物理机pmj能形式化描述成式(1)
pmj={idj,cpuj,memj,bwj,diskj,alivej}
(1)
在式(1)中,idj表示第j台物理机在数据中心的唯一标识,cpuj表示第j台物理机的CPU核心数,memj表示第j台物理机的内存大小,bwj表示第j台物理机的带宽大小,diskj表示第j台物理机的磁盘大小,alivej∈{0, 1} 表示第j台物理机是否处于活跃状态。
数据中心的虚拟机vmi的资源需求描述可以形式化描述成式(2)
vmi={idi,cpui,memi,bwi,diski}
(2)
其中,idi表示第i台虚拟机在数据中心的编号,cpui表示第i台虚拟机的CPU核心数,memi表示第i台虚拟机的内存大小,bwi表示第i台虚拟机的带宽大小,diski表示第i台虚拟机的磁盘大小。
2.2 资源损耗模型
由于同一台物理机上往往运行着数台异构的虚拟机,不同规格的虚拟机对计算机资源的占用率不同,这有可能会导致物理机某一维度的资源利用率过高,而其它维度的资源未能充分利用,造成计算资源的极大损耗。不合理的虚拟机放置位置,会导致数据中心的负载失衡。
图2为在仅考虑CPU、内存资源时数据中心的资源损耗案例。某一台物理机上先放置了3台异构的虚拟机,剩余可用资源为20%的CPU和30%的内存。若此时用户请求一台资源需求为30%的CPU和30%的内存的虚拟机,数据中心将由于这台物理机的CPU资源不足,开启一台新的物理机来处理该虚拟机创建请求,造成更大的资源浪费和系统能耗。
在考虑数据中心资源损耗时,物理机具有的资源维度和虚拟机请求的资源维度是相同的。假设物理机pmj上运行着k台虚拟机,R={cpu,mem,bw,disk} 为物理机的资源集合,r∈R,rj表示物理机pmj的r类资源配置量,ri表示部署在物理机pmj上的虚拟机vmi(i=1,2,…,k) 的r类资源配置量。物理机pmj的r类资源利用率可以表示为式(3)
(3)
将数据中心中各类资源的利用率的均值作为数据中心的平均资源利用率。用Uavg表示数据中心总的平均资源利用率,其计算方式如式(4)所示
(4)
使用标准差来衡量数据中心资源分配的偏离程度Lose,Lose的计算过程能形式化描述为式(5)
(5)
将Lose作为数据中心资源损耗优化目标函数,Lose值越小表示数据中心负载越均衡,即资源损耗越少。
2.3 虚拟机放置的约束优化模型
假设物理机pmj上放置着k台虚拟机,θ为物理机在保障用户服务质量情况下所能提供最大资源的比例。由此得到一个虚拟机放置约束优化模型,可形式化描述为式(6)
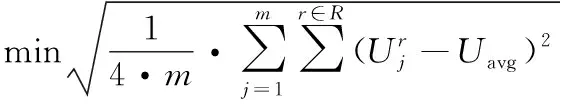
(6)
其中,式(6)中的第一个约束条件表示部署在一台物理机上所有虚拟机请求的资源总和不能超过物理机在保证服务质量情况下所能提供的资源。式(6)中的第二个约束条件表示数据中心中所有虚拟机请求的资源总和不能超过数据中心在保证服务质量情况下所能提供的资源。
3 SCRLPSO算法
在标准PSO算法[18]中,每个粒子代表一个解空间的解。种群中的每个粒子通过速度-位置计算模型进行种群迭代,每次迭代根据自己的当前位置、速度、全局最优解和个体历史最优解来更新自己的位置和速度[19,20]。
虚拟机放置问题是一个典型的离散型问题。传统的PSO算法在解决离散型问题时,存在编码解码复杂、容易陷入局部最优解、收敛速度慢和不能动态调整全局搜索和局部搜索的关系等问题。为此,在传统的PSO算法的基础上,使用连续整数编码方式替换传统的二进制编码方式,结合反向学习策略来提高种群的收敛速度,采用开口向下的抛物线的权重更新策略在运行中动态调整搜索权重,通过正余弦扰动来避免陷入局部最优解,提出了一种SCRLPSO算法。
设种群规模为N,维度为D,最大迭代次数为T,第i个粒子的位置为xi=(xi1,xi2,…,xiD), (i=1,2,…,N), 速度为vi=(vi1,vi2,…,viD), 第i个粒子迄今为止搜索到的最优位置为pi=(pi1,pi2,…,piD), 种群今为止搜索到的最优位置为g=(g1,g2,…,gD)。 标准粒子群算法利用式(7)、式(8)来更新粒子速度和位置
vij(t+1)=ω·vij(t)+c1r1(t)[pij(t)-xij(t)]+c2r2(t)[gj(t)-xij(t)]
(7)
xij(t+1)=xij(t)+vij(t+1)
(8)
其中,t表示当前迭代次数,xij(t) 表示t时刻粒子i的第j维的位置,vij(t) 表示t时刻粒子i的第j维的速度,ω为保持原有速度的权重,c1和c2称为学习因子,r1和r2为[0,1]之间的均匀随机数。
3.1 编 码
标准PSO算法适合于连续型问题的寻优,针对离散型问题需要对问题进行编码。常用的二进制编码方式在对虚拟机放置问题进行编码时,一个n×m的01矩阵代表一个解,第i行代表第i台虚拟机的放置位置。由于虚拟机的不可分割性,每台虚拟机仅能放置在一台物理机上,故每一行仅能有一个数字为1。如图3所示,图3左侧是一个4×3 的01矩阵,描述的是将4台虚拟机放置到3台物理机上的一个放置方案的编码。图3右侧表示每一台虚拟机放置的实际物理机序号。计算编码所对应的n个虚拟机放置位置,需要一个解码的时间。此外,使用二进制编码在位置更新时,要求考虑每个虚拟机仅能放置在一台物理机上的约束。必须在位置-速度计算模型添加额外的模块来保证约束的实现,造成不必要的计算资源浪费。
针对上述二进制编码的不足,本文采用一种连续整数编码方式。根据虚拟机和物理主机的映射关系,以虚拟机为单位,每个虚拟机仅能放置到一个物理主机,使用一个m维向量表示解的编码,向量中的每个属性为物理机编号,如x={x1,x2,…,xn},xi∈{1,2,…,m},i∈{1,2,…,n}。 向量xi的维度为n,每个维度的取值为[1,m]之间的整数。例如,xi=q, 表示第i台虚拟机放置在第q台物理机。采用连续整数编码的方式,可以很好地适用于位置-速度计算模型。并且编码即位置,编码和位置保持高度的一致性,节省了编码解码的时间,提高算法的运行效率和求解精度。
3.2 种群初始化策略
种群收敛速度在一定程度上受个体距离最优解的距离的影响。如果种群中每个个体都距离最优解较近,那一定程度上能提高种群收敛速度。考虑每个个体和它的反向个体,有更高的几率接近最优解[21]。在初始化种群时,生成种群的反向种群。将种群中个体和它的反向个体进行比较,选择Lose更小的个体作为种群的初始个体,构成初始种群。
对于反向解,它的值为解的位置的每一位的反向取值。对于种群中第i个个体xi=(xi1,xi2,…,xiD), 它的反向解定义为
xi-=(m+1-xi1,m+1-xi2,…,m+1-xiD)
(9)
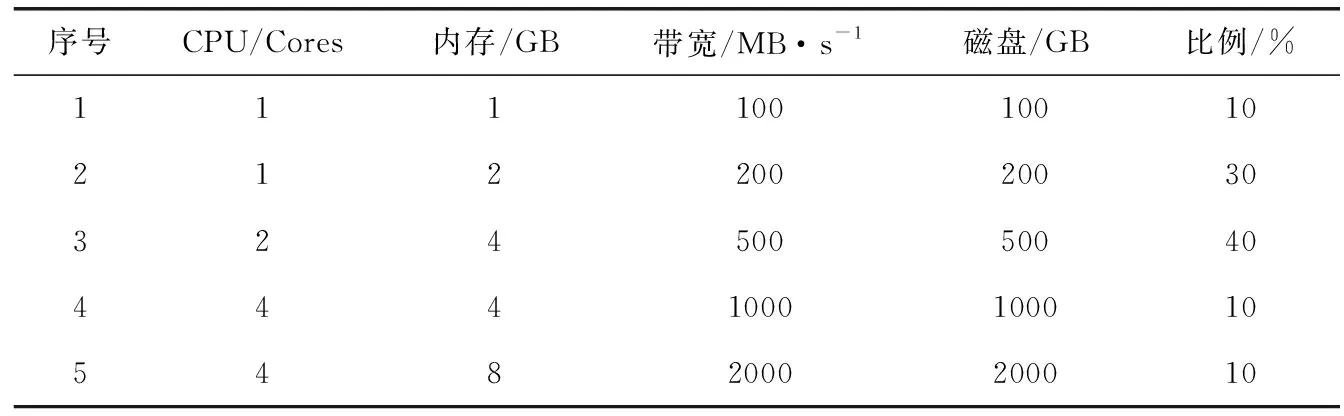
SCRLPSO算法将初始种群作为反向学习个体,增加了初始解的多样性,使初始种群更加接近最优解。使用式(9)来生成xi的反向解xi-,若Lose(xi) PSO算法在寻优的过程中,可以分为局部挖掘和全局搜索两类,也称为开发和探索。这两个部分相互促进又相互矛盾,全局搜索用于快速定位最优解的范围,而局部挖掘用于寻找最优解。全局搜索过多的时候,收敛速度会变慢,求解精度降低;局部挖掘过多的时候,就容易陷入局部最优解。在种群迭代的过程中必须权衡二者的关系。PSO算法使用权重系数ω来处理开发和探索的关系,常用的惯性权重策略有线性递减权值策略和指数曲线、开口向下抛物线、开口向上抛物线等非线性权重策略。 标准PSO算法使用线性递减权值策略,ω随着迭代次数线性递减。当大量的虚拟机部署在云平台上时,采用线性递减权值策略使算法全局搜索能力强,但后期收敛速度慢,求解精度低。所以本文采用自适应权重开口向下曲线来动态调节开发和探索的能力,如式(10)所示。保证算法在前中期保持较强的全局搜索能力,后期权重快速下降,具有较强的局部搜索能力。ωmax、ωmin为最大权重和最小权重 (10) 传统的粒子群优化算法具有较好的全局搜索能力,但是后期局部搜索能力不足,求解精度低。针对粒子群优化算法局部搜索时的随机性,本文以概率rc采用正余弦扰动对粒子进行位置更新。采取当前可能不好的解,有利于跳出局部最优解,增强算法的全局寻优能力。正弦余弦算法是一种新型元启发式算法[22],通过非线性方式调整参数来提高算法的搜索能力。本文结合正余弦策略,使用式(11)~式(14)来更新粒子速度和位置。 r为在[0,1]之间均匀随机取值,若r>rc vi(t+1)=ω(t)·vi(t)+c1r1[pi(t)-xi(t)]+c2r2[g(t)-xi(t)] (11) (12) 否则 vi(t+1)=vi(t) (13) (14) 其中,rc为扰动概率,若r>rc,使用PSO算法的位置-速度计算模型来更新粒子的速度和位置,否则使用正余弦扰动来更新粒子。在式(12)~式(14)中,将位置的浮点型数值转化为整型,并约束在[1,m]之间,表示物理机的序号。t表示当前迭代次数,xi(t)表示t时刻粒子i的位置,vi(t)表示t时刻粒子i的速度,ω(t)为t时刻保持原有速度的权重因子,c1为个体向自身学习能力因子,c2为个体向种群学习能力因子,r1和r2为[0,1]之间的均匀随机数,ω(t)为粒子第t代的惯性因子,r3取值为[0,2π]均匀分布的随机数,r4为[0,2]之间均匀分布的随机数,控制和当前全局最优解之间的距离,r5为取值为[0,1]的随机数,控制正弦和余弦的转换概率。 最终设计出SCRLPSO算法如算法1所示。 算法1:基于正余弦扰动和反向学习的自适应粒子群优化算法 输入参数:pms:数据中心物理机资源列表 vms:数据中心虚拟机请求列表 xbound:粒子位置范围 vbound:粒子速度范围 ωbound:权重范围 T:终止进化的代数 M:种群规模 输出参数:g:最优方案 (1)t←1; (2)ProcedureSCRLPSO(pms,vms,xbound,vbound,ωbound,T) (3)foriinM (4)X(t)[i]←Code(pms,vms,xbound,vbound); (5)endfor (6)forxinX(t)do (7)x-←reverse_learning(x); (8)ifLose(x-) (9)x←x-; (10)endif (11)endfor (12)while(t<=T)do (13)weight=getweight(t); (14)fori=1toMdo (15)X(t)[i]←updatexv(wright,t,X(t)[i]); (16)endfor (17)X(t+1)←X(t); (18)t←t+1; (19)g←updateglobalbest(); (20)fori=1toMdo (21)p[i]←updatehistorybest(wright,t,p[i]); (22)endfor (23)endwhile (24)endProcedure 其中,X(t) 表示t时刻种群的所有个体,包含个体的位置和速度,第(3)行~第(10)行表示种群初始化操作,第(13)行更新当前代数种群的权重,第(14)行~第(16)行更新种群中个体的位置和速度,第(19)行~第(22)行更新种群全局最优解和个体历史最优解。 本文采用Python语言对算法进行了实现,通过和标准PSO算法、最佳适应法、首次适应法进行对比分析来验证SCRLPSO算法在虚拟机放置问题上降低资源损耗的有效性。实验模拟了50台同构的物理机组成云平台,物理机的配置为36核CPU、95 GB内存、10 000 MB带宽和10 TB磁盘。 实验中,最佳适应算法依次选择所有处于活跃状态的物理机中能满足虚拟机需求的,且剩余资源最小的物理机来进行放置。以内存利用率为指标对物理机升序排序,依次判断物理机是否满足虚拟机要求,直到某个物理机能够放置虚拟机,此时选择的物理机就是最优选择。若检查到最后一台物理机仍不能放置,则要求唤醒新的物理机进行放置。 首次适应算法根据物理机序号依次判断能否放置虚拟机,若能放置则将虚拟机放置在这台物理机上,否则判断下一个物理机。直到检查完所有物理机,若仍不能放置,则要求唤醒新的物理机进行放置。 根据OpenStack的flavor套餐提供的虚拟机参数规格,同时对虚拟机进行带宽限制,虚拟机具体的参数规格见表1。 表1 虚拟机规格 SCRLPSO算法主要的参数见表2。 [xmin,xmax] 为粒子位置范围, [vmin,vmax] 为粒子速度范围,用来约束粒子,以免越界或速度过快错过最优解。rc正余弦策略的扰动概率,用来切换位置更新公式,θ为保障服务质量的情况下所能提供的最大资源利用率。 表2 SCRLPSO算法参数 (1)资源损耗分析 本文以资源损耗为评价指标,在相同数量和规模的虚拟机请求下,比较各个放置策略的资源损耗度,根据式(5)得到每种策略的最优放置方案的资源损耗度。由于资源利用率取值区间为[0,1],计算Lose时得到的数据偏小,所以对资源利用率做去掉百分号处理,每种策略执行20次取其均值作为结果。 图4描述的是SCRLPSO算法、PSO算法、BF算法、FF算法在4组虚拟机请求的资源损耗情况。从图中可以看出,在相同的虚拟机请求数量下,SCRLPSO算法的资源损耗度相较于BF算法、FF算法、PSO算法更小。实验结果表明,数据中心资源损耗并不随着虚拟机数量而线性变化,而是针对云平台资源分布情况。如果当前的数据中心资源不足以放置所有的虚拟机,则数据中心需要开启新的物理机来承载虚拟机的资源请求。经过本文的优化策略后,虚拟机被均匀分配到各个物理机上,使得数据中心资源分配相对均匀,减少了资源损耗。 (2)SLA违背率分析 服务质量是评价云服务的重要指标之一,通常SLA和物理机的资源利用率相关。当物理机的资源利用率提高时,服务质量快速下降。本文将数据中心的SLA违背率定义为 fSLA=ln(2+Uavg-θ) (15) 图5描述的是SCRLPSO算法、PSO算法、FF算法、BF算法随着虚拟机请求数量的增加,数据中心的服务质量的变化情况。SCRLPSO算法相对于传统的FF算法,SLA违背率平均降低了7%,比BF算法的SLA违背率降低了6%,比标准PSO算法的SLA违背率降低了1%。故SCRLPSO算法更能保证用户的服务质量。传统的BF算法、FF算法等基于贪婪策略的启发式算法,主要目标是尽可能减少处于活跃状态的物理机的数量来提高资源利用率,与尽可能提高服务质量的目标冲突,很可能会导致服务质量的下降。本文提出的虚拟机放置策略,能在尽可能减少资源损耗的同时,保障用户的服务质量。 (3)收敛速度对比 图6描述的是SCRLPSO算法和PSO算法在不同虚拟机请求下的平均收敛速度。SCRLPSO算法的收敛速度比PSO算法提高了50%。这是因为SCRLPSO算法融合了反向学习策略,使得初始解更接近最优解。在权重更新策略上采用开口向下抛物线,同时使用正弦余弦算法来扰动粒子更新过程,增强种群的全局搜索能力,提高搜索精度。故SCRLPSO算法相较于标准PSO算法具有更快的收敛速度。 本文提出了基于SCRLPSO算法的虚拟机放置策略。该策略考虑CPU、内存、网络带宽和磁盘4种计算机系统资源,针对云平台中普遍存在的资源损耗进行分析,提出了最小化资源损耗的优化目标函数模型,在标准的粒子群算法的基础上对编码和权重进行改进,使其更适合于求解虚拟机放置问题。混合正弦余弦算法,能够有效地避免陷入局部最优解,提升求解精度。同时结合基于反向学习的种群初始化策略,能够加快种群收敛速度。仿真实验的结果表明,在数据中心资源配置和虚拟机请求一定的情况下,本文方法相对于标准粒子群算法、最佳适应法、首次适应法更能减少数据中心资源损耗,进而降低能耗,减少数据中心运营成本。下一步将对虚拟机调度问题进行多目标优化,进一步提高云平台的综合性能。3.3 自适应权重
3.4 位置更新模型

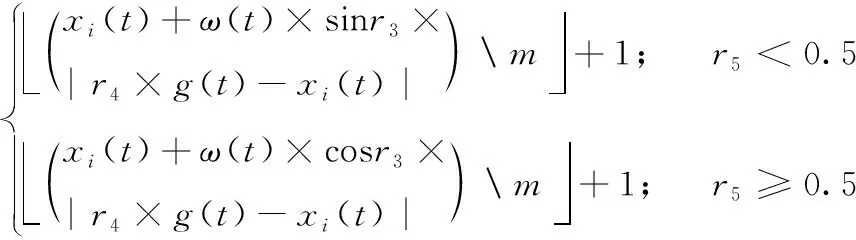
4 实验设计与结果分析

5 结束语
