考虑电力系统静态稳定增强的海上多端直流系统规划优化
2022-10-17黄玲玲王启国应飞祥魏书荣
黄玲玲,王启国,符 杨,应飞祥,魏书荣,刘 阳
(上海电力大学电气工程学院,上海市 200090)
0 引言
海上风电作为近年来发展最迅速的可再生能源形式之一,已成为绿色能源领域发展与研究的热点[1-2]。规模化、集群化、深远海化海上风电发电的经济输送与安全并网已成为中国新时期“双碳”战略目标下海上风电大规模开发亟待解决的关键问题之一。多端柔性直流输电方式由于具备柔性直流输电在远距离、大容量功率传输中优良的经济性、可控性等优势,在海上风电集群并网中获得越来越多的关注。其中,多端直流(MTDC)输电技术被认为是解决中国新能源并网与消纳的有效技术手段之一[3]。
国内外针对MTDC 系统应用于解决大规模风电并网问题的方式方法进行了广泛且深入的研究。在网络拓扑结构方面,MTDC 系统具有包含辐射状、环形、混合结构等多种形式的网络拓扑结构[4-5]。在运行性能方面,系统的网络拓扑、控制策略及控制参数等均可能在不同方面对系统的运行性能产生不同程度影响[6-8]。小信号模型分析是MTDC 系统稳定性分析的基础,文献[9-10]针对MTDC 系统换流站不同的控制方式,结合风电机组接入等因素构建了MTDC 系统小信号模型,研究了含风电场的MTDC 系统小信号稳定性。但是,现有的MTDC系统小信号稳定性研究大多是基于给定的直流网络拓扑展开的。而对于大规模海上风电场集群经MTDC 系统并网的电气系统规划设计来说,MTDC系统网络拓扑不仅影响系统的运行性能,还与MTDC 系统的规划投资经济性息息相关,基于单一网络拓扑的MTDC 系统小信号模型不能满足系统规划对不同方案的经济成本、并网性能等多方面指标进行综合评价的需求。因此,有必要结合MTDC 系统灵活的网络结构形式,构建一种适用于优化规划的考虑可变网络拓扑的MTDC 系统小信号模型。
当MTDC 系统接入陆上交流电网时,馈入交流电网的电力电子设备数量的增多和容量的增大,将对陆上电网的稳定运行产生不同程度的影响[11]。为了评估大容量直流系统接入对交流电网的影响,国际大电网组织(CIGRE)提出了一种基于多馈入相互作用因子的多馈入短路比指标[12]。为了进一步明确交流系统强弱的影响,文献[13]从特征根角度提出了一种广义短路比(generalized short-circuit ratio,gSCR)指标,文献[14-15]在gSCR 指标的基础上,提出了一种临界gSCR 的计算方法。但是,上述研究大多采用固定的单电源等值方式对陆上交流系统进行简化与等效。然而,对于大规模海上风电场集群经MTDC 系统多点并网的系统规划问题来说,考虑到MTDC 系统内部潮流的大小和方向具备一定的可控性,为了更好地适应陆上交流电网运行的需要,有必要充分利用海上风电场集群在广阔空间上分布带来的多个待选公共连接点(PCC)并网的优势,优选陆上并网点。这需要进一步对PCC 变化条件下的gSCR 计算方法进行研究。
针对上述问题,本文围绕海上风电集群经MTDC 系统接入交流电网的优化规划问题,充分考虑MTDC 系统灵活多变的网络拓扑结构、MTDC系统与陆上交流电网并网点一定范围内可优化的特性,构建了一种兼顾经济性与并网稳定性指标的海上风电场MTDC 系统优化模型。算例结果分析表明,本文构建的综合目标优化模型,能够在保证规划方案投资成本的情况下明显改善系统稳定性,可为海上风电经MTDC 系统并网的工程设计提供参考。
1 问题描述及思路框架
1.1 问题思路与研究框架
对于海上风电功率经MTDC 系统接入电网的规划问题来说,主要目标是确定海上换流站的数量、位置、容量,陆上换流站的数量、位置、容量,以及海上、陆上换流站之间的网络拓扑与网络参数。通常来说,海上换流站的数量、位置和容量主要取决于海上风电场集群的容量、地理分布以及汇集多个海上风电场交流升压站的传输功率,其选址定容需在海上风电场内部交流系统与高压直流输电系统成本之间选取最佳平衡点,其优化方法与交流系统规划具有较大的相似性。为了突出本文的主要工作,关于海上换流站的选址定容优化部分,将借鉴文献[16]中的方法并进行简化。因此,在本文中将不做重点阐述,即默认海上换流站位置和容量为已优化的结果。而陆上换流站的选址、容量优化不仅受限于海上换流站的位置与容量,进而影响MTDC 系统网络的拓扑结构,还可能显著影响接入的陆上交流电网的稳定运行水平,这是本文研究的主要内容。
考虑到海上风电集群经MTDC 系统并网规划是一个需要兼顾投资经济性与大规模海上风电功率并网稳定性的综合优化问题,本文基于MTDC 系统可变拓扑结构的小信号模型与相应网络下的MTDC 系统成本计算,提出了单位稳定裕度成本指标,并构建了考虑单位稳定裕度成本与PCC 可变条件下gSCR 的综合优化模型。最后,采用传统的遗传算法进行优化求解。综合指标的构建思路如图1所示。

图1 模型构建思路Fig.1 Model construction idea
1.2 MTDC 系统网络拓扑矩阵
在MTDC 系统中,直流海缆将不同数量的海上/陆上换流站以不同的方式相互连接,形成简单或复杂的海上直流网络,以满足不同规模、不同离岸距离的海上风电场的并网需求。MTDC 系统的网络结构复杂多变,但概括来说,大致可以分为包含环形结构的网络拓扑形式与不包含环形结构的网络拓扑形式2 种,具体示意图见附录A 图A1。
考虑到海上直流网络拓扑是影响MTDC 系统投资经济性与系统稳定性的关键环节,为了直观地描述海上直流网络拓扑对海上风电经MTDC 系统并网规划方案的影响,本文提出了一种MTDC 系统网络拓扑连接矩阵的定义方法。为了便于进行MTDC 系统小信号建模,对于一个具有n个换流站、m条直流电缆的MTDC 系统来说,定义其网络拓扑连接矩阵PT为:

式中:PT为m×n矩阵,pT,ab为其元素。pT,ab=0 表示第a条线路与节点b不相连;pT,ab=1 表示第a条线路与节点b相连且支路电流方向为流出该节点;若pT,ab=-1,表示第a条线路与节点b相连且支路电流方向为流入该节点。
基于上述定义,可以得到任意MTDC 系统网络拓扑条件下的直流海缆投资成本Ccable,即

式中:cij为换流站i与换流站j之间的单位海缆成本,取决于网络潮流分布;Lij为换流站i与换流站j之间的海缆长度;Hij为换流站连接矩阵H中的元素,Hij=1 表示换流站i与换流站j相连接,Hij=0 表示换流站i与换流站j不连接。H矩阵可由网络拓扑连接矩阵PT得到,具体表达式见式(3)。

式中:Hii为H矩阵中的对角元素。
2 稳定性指标推导
大规模海上风电功率经MTDC 系统接入陆上交流电网,一方面,陆上交流电网的结构和参数将对PCC 的接入功率产生限制;另一方面,不同的MTDC 系统并网方案也对陆上交流电网表现出不同程度的影响。为了定量评估不同MTDC 系统规划方案对MTDC 系统自身运行稳定性与接入的陆上交流电网运行稳定性的影响,本文构建了2 个静态稳定性指标:MTDC 系统稳定裕度与gSCR。前者主要基于可变网络拓扑的MTDC 系统的小信号模型,后者主要基于可变PCC 交直流系统gSCR 分析。
2.1 MTDC 系统稳定裕度指标
1)换流站线性化模型

国内外许多专家和学者对电压源换流器(VSC)系统换流站的小信号模型进行了充分深入的研究[7-10,17-20]。为了简化说明,基于文献[17-20]的研究,构建的VSC 系统换流站的小信号模型如式(4)所示。其中,换流站中的换流器与交流系统结构如附录A 图A2 所示,控制系统如图A3 所示,锁相环如图A4 所示,输电线路如图A5 所示。式中:id和iq分别为换流站交流侧d、q轴电流;t为时间;upq为PCC 处电压up在q轴的分量;ucd和ucq分别为换流站出口处电压uc在d、q轴的分量;usd和usq分别为交流电网等效电压源us在d、q轴的分量,需要由锁相环(PLL)的参考角度得到;ω为系统的角频率;udc为换流站直流电压;iline为直流线路上的电流;Ls和Rs分别为换流器与PCC 之间的电感和电阻;Ln和Rn分别为交流系统或风电场侧的等效电感和电阻;C为直流滤波电容;θpll为PLL 控制器输出的相角;Tδ为开关周期;、、、、、为比例-积分(PI)控制器参数;z1、z2、z3、z4为外环电压、内环电流积分器输出值;Sd为有功类控制中间变量;Sq为无功类控制中间变量;xpll为积分环节输出信号;和为内环控制参考值;u和u分别为控制器输出调制信号在d、q轴的分量;上标o 表示对应变量的稳态值;Δ 表示对应变量的扰动量。
2)基于网络拓扑矩阵PT的直流线路线性化模型
一条直流线路可以采用π 形等值电路。海缆线路分布电容可以与换流器端口电容进行合并,即可得到直流线路等效电路,如附录A 图A5 所示。因此,一条直流线路的数学模型可以表示为:
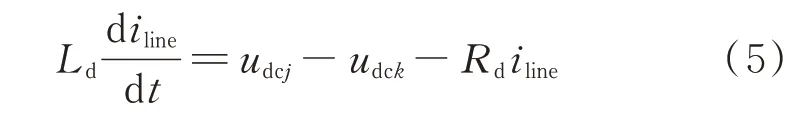
式中:Ld和Rd分别为直流线路的电感和电阻;udcj和udck分别为换流站j和k的直流母线电压。
对式(5)线性化处理,得到直流输电线路小信号模型为:

当考虑MTDC 系统具有复杂多变的网络拓扑结构时,可以在式(6)的基础上进行拓展与修正,进而得到任意拓扑结构PT下的直流输电线路小信号模型为:
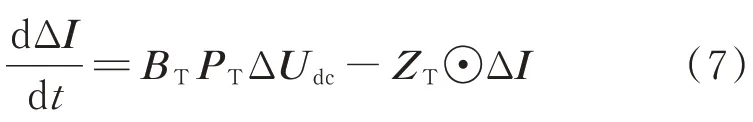
式中:ΔI=[Δi1,Δi2,…,Δim]T为直流线路电流变化量矩阵;ΔUdc=[Δudc1,Δudc2,…,Δudcn]T为换流站直流电压变化量矩阵;BT和ZT为系数矩阵,具体表达式为:BT=diag [1/Ld,1,1/Ld,2,…,1/Ld,m],ZT=[Rd,1/Ld,1,Rd,2/Ld,2,…,Rd,m/Ld,m]T,其中,Ld,m和Rd,m分别为第m条直流线路的电感和电阻;⊙表示矩阵的Hadamard 积。
3)全局小信号模型
将换流器、控制系统、直流线路等线性化模型进行联立,可以得到多端柔性直流输电系统小信号模型。其全局模型可以表示为:

式中:ΔX为状态变量;Δu为输入变量;Asys为状态特征矩阵,考虑到可变网络拓扑的影响,Asys是一个11Non+7Noff+m阶方阵(Noff为海上换流站数量,Non为陆上换流站数量);Bsys为系统状态空间方程输入矩阵。
4)稳定裕度指标
根据劳斯判据中稳定裕度的定义[21]:一个稳定系统的特征方程的根落在复平面虚轴左半部,而虚轴是系统的临界稳定边界,因此,以特征方程最靠近虚轴的根和虚轴的距离表示系统的稳定裕度。据此,针对MTDC 系统小信号稳定模型,构建MTDC系统的稳定裕度指标,即

式中:σ为MTDC 系统稳定裕度;λ(·)表示求特征值;Re(λ)表示对特征值λ取实部。当存在实部大于0的特征根时系统不稳定,因此,针对稳定条件,即特征根均落在复平面虚轴左半部的条件取稳定裕度,σ越大,系统越稳定。
2.2 交流系统稳定裕度指标
上述分析主要是从MTDC 系统的角度对系统的稳定裕度进行了分析与定义。对于大规模海上风电经MTDC 系统接入陆上电网的规划问题来说,当海上风电功率从不同的PCC 以不同的容量接入时,也将对陆上交流电网的稳定水平产生显著的影响。考虑到海上风电集群空间分布较广,电网运行与规划部门能够结合陆上电网的实际情况,提供多个待选PCC,因此有必要在多个待选PCC 中优选最佳的PCC 及其接入容量。本文基于文献[14]构建的gSCR 指标,进一步考虑PCC 变化对gSCR 指标的影响,提出了一种基于戴维南等效原理的可变多PCC 的gSCR 计算方法。
为了对可变多PCC 的gSCR 计算方法和过程进行详细阐述,结合一个14 节点的交流系统(见附录A 图A6(a),其中红色节点为交流电网给出的待选PCC)进行说明。首先,根据多端戴维南等效原理,对图A6(a)所示复杂网络进行等效,得到如图A6(b)所示的从D个待选PCC 看到的等效交流系统简化模型。然后,考虑PCC 的动态优化过程,当某一场景下,实际优选的PCC 为任意给定的G(G≤D)个PCC 时,则该交流网络将进一步等效为图A6(c)所示的包含G个等值电压源的系统网络。
初始网络与等效网络转化过程中的等效参数计算方法如下(推导过程见附录B):
1)将D个待选PCC 从1 开始进行编号。从D个待选节点中选取给定的G(G≤D)个PCC,该选定的PCC 集合记为Γ(如Γ={1,2,3}表示选取编号1、2、3 的节点为PCC)。
2)根据PCC 端口电压特性,对G个PCC 连接阻抗进行等效,得到:

式中:yh0为等效前h节点与等效交流电源之间的导纳;yhe为等效前h节点和e节点间的导纳;y′h0为等效后h节点与等效交流电源之间的导纳;khe为导纳折算系数,表示e消去节点对h节点的导纳折算系数;ue和uh分别为e节点电压和h节点电压;uN为交流系统额定电压;Λ为消去节点集合。
3)根据交流潮流计算得到待选PCC 节点电压u1,u2,…,uD。
4)根据等效后的G个PCC 交流网络列写等效阻抗矩阵B(G×G)。
由此,可以得到不同PCC 接入条件下的gSCR(RgSCR):

式中:SB为换流站额定容量矩阵。根据文献[14]可知,矩阵-S-1BB是一个实对称矩阵,所以特征值均为实数,且RgSCR≥0 时,系统稳定,gSCR 越大,系统越稳定。
3 综合优化模型
3.1 目标函数
通过上述分析可以看出,MTDC 系统中换流站的容量、网络拓扑不仅直接决定系统的投资成本,同时也直接影响MTDC 系统的稳定裕度与并网交流系统的gSCR,三者表现出明显的耦合关系。因此,为了对MTDC 系统进行全面优化,本文采用归一化的方法,构建了包含单位稳定裕度成本和gSCR 的综合目标函数,如式(12)所示。考虑到对于海上MTDC 系统来说,换流站故障是海上直流系统停运的主要原因,而海缆故障率较低且多为外力破坏所致[22-24],因此,本文在建模过程忽略了海缆可靠性因素的影响。
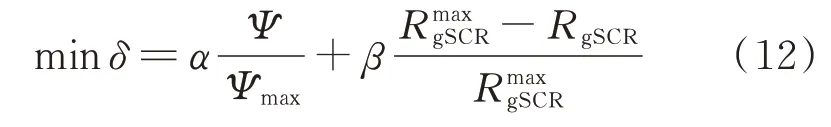
式中:δ为反映综合指标的目标函数;Ψ为单位稳定裕度成本,同时反映MTDC 系统设备参数、网络拓扑变化对投资成本及稳定裕度σ的影响,具体定义如式(13)所示;Ψmax为单位稳定裕度成本最大值;RmaxgSCR为gSCR 最大值;α和β分别为单位裕度投资成本与gSCR 的权重系数。

式中:Ctotal为系统总投资成本,主要包括换流站建设成本Cconverter与直流海缆成本Ccable,具体表达式如下。

换流站的成本主要考虑换流阀的设备成本、平台的建设安装成本以及换流站配套电气设备与控保装置等费用。其中,海上换流站由于平台与建设成本高昂,这里也单独计入,即

式中:C和C分别为海上换流站与陆上换流站的建设总成本;C和C分别为第i个海上换流站换流阀与陆上换流站换流阀的设备成本,两者主要取决于换流阀类型和待优化变量——换流站额定容量,具体计算方法可以依据文献[25]得到;C,i为第i个海上换流站的海上平台造价(含建设成本);为第i个海上换流站配套电气设备与控保装置等费用;为第i个陆上换流站配套电气设备与控保装置费用。
3.2 约束条件
约束条件主要包含2 个方面:1)直流系统的运行约束;2)海上风电功率的并网约束。其中,直流系统运行约束为:

式中:Ia第a条线路实际电流;Imaxa为线路允许的最大电流;Ub为节点b的实际电压;Umaxb和Uminb分别为系统中节点b允许的最大、最小电压。
海上风电功率的并网约束是指规划方案必须满足在额定条件下海上风电功率能够经MTDC 系统全部接入陆上电网的要求。因此,在考虑陆上换流站N-1 约束条件下,主站的额定容量PMN需要留有一定的裕度,即PMN能够平衡因从站退出而产生的不平衡功率,因此,主站的额定容量可以表示为主站正常运行时的容量与从站的最大额定容量之和,即

式中:P={P1,P2,…,Pi,…,PNon}表示陆上换流站i额定功率Pi的集合;O为陆上换流站主站的额定功率集合;max {PO}表示除去陆上换流站主站额定功率的陆上换流站额定功率集合中的最大额定功率;Ptotal为海上风电总功率。
海上风电功率并网还应满足相关的稳定性约束,即

可以看出,上述模型是一个典型的多离散变量的非线性优化问题。考虑到一定规模的海上风电场集群中MTDC 系统换流站的数量通常是有限的并且数量相对较少,本文采用传统的遗传算法对上述模型进行优化求解,具体过程见文献[26-27],这里不再赘述。
4 算例分析
4.1 算例介绍
为了对本文提出的模型与方法进行详细说明,构建了如附录A 图A7 所示的海上风电集群并网系统。其中,海上风电集群额定功率为1 600 MW。根据文献[16]优化方法,事先确定了2 个海上换流站的位置与容量;根据图A6 所示交流网络等效方法,陆上交流电网给出了4 个待选的PCC 节点,如图A7 所示,相应的PCC 短路容量数据如表A1 所示。换流站及相关交流电网的主要参数如表A2 所示。换流站相关成本计算方法见文献[25],直流海缆数据由设计单位提供。
4.2 小信号模型验证
为了验证本文所提出的小信号模型的正确性,在Simulink 中搭建了一个三端MTDC 系统的仿真模型。其中,换流站1 采用定直流电压控制,换流站2、3 采用定功率控制,具体见附录A 图A8。
仿真过程中,设置在t=1 s 时,换流站2 有功功率发生0.1 p.u.的功率增量变化,依据上文构建的小信号模型计算得到换流站2 的直流电压、交流侧d、q轴电流波形与Simulink 仿真结果的对比如附录A 图A9 至图A11 所示。从小信号模型计算结果与仿真波形对比来看,本文推导的小信号模型计算结果较好地吻合了仿真结果,说明了本文所构建的小信号模型的正确性。此外,基于可变拓扑矩阵的小信号模型计算速度较快,能够满足规划过程中多次迭代计算的需要。
4.3 最优方案
采用本文所提模型与方法对算例进行优化求解,得到综合指标最优的MTDC 系统连接方案(α=0.5,β=0.5)如下:MTDC 系统包含2 个海上换流站与3 个陆上换流站,其中,换流站1 为主换流站,容量为1 100 MW,其他换流站容量为500 MW;换流站分别从待选的节点2、3、4 接入;MTDC 系统及其与陆上交流电网的连接拓扑如图2 所示。其中,红色点表示待选PCC,黑色虚线表示直流电缆。

图2 最优拓扑连接方案Fig.2 Optimal topology connection scheme
4.4 结果分析
由式(12)可知,上述优化结果由综合评价指标δ决定,而综合评价指标的大小取决于系统总投资成本Ctotal、直流系统稳定裕度σ和gSCR。为了研究MTDC 系统稳定裕度指标对规划结果的影响,分别对比了考虑MTDC 系统稳定裕度指标的最优规划方案(记为方案A)与不考虑MTDC 系统稳定裕度指标的最优规划方案(记为方案B)2 种结果的系统投资成本、系统稳定裕度以及综合评价指标。附录A 图A12 给出了2 种方案的最优拓扑。为了便于显示与分析,这里分别以方案B 的相关结果为基准(即该值取100%),以百分比的形式显示2 种方案的相关指标对比情况,结果如图3 所示。
结合图3 和附录A 图A12 可以看出,海上风电经MTDC 系统规划过程中考虑稳定性因素的影响,将导致规划方案的成本有一定程度提高,在本算例之中,方案A 的成本较方案B 约高14%。分析其原因,主要是由于方案A 中换流站与直流线路的数量增加所导致。但是,结合指标Ψ与gSCR 的差异,可以看出:1)考虑单位稳定裕度成本能够有效兼顾规划成本与稳定水平;2)在MTDC 系统规划过程中考虑MTDC 系统的小信号稳定水平,有益于MTDC系统接入交流电网的稳定性。附录C 中对本文提出的计及稳定性因素影响的海上风电经MTDC 系统接入规划进行了更详细的论证与说明。
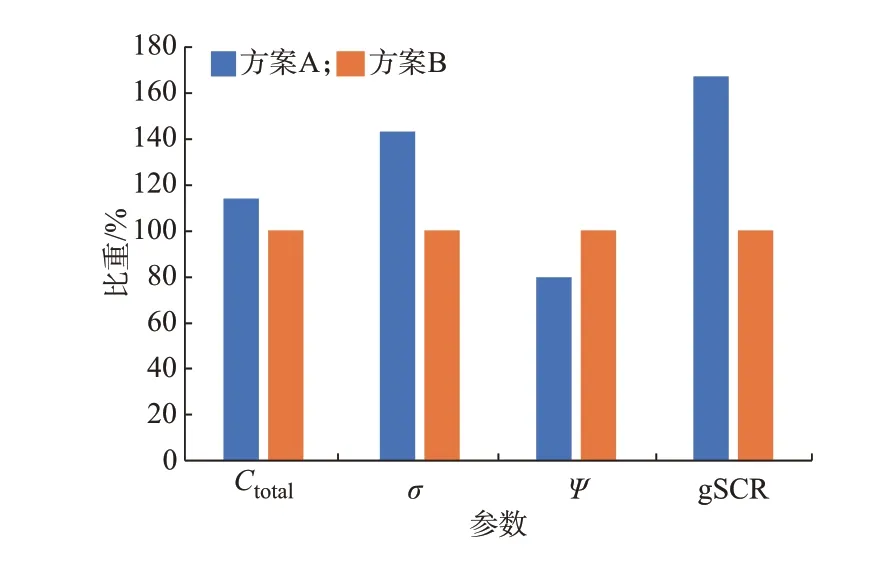
图3 方案A 和方案B 对比Fig.3 Comparison of scheme A and scheme B
为了进一步对影响MTDC 优化方案的主要因素进行分析,下面主要针对直流海缆选型、MTDC系统网络拓扑以及PCC 选择等方面分别进行讨论。
1)直流海缆选型的影响
网络拓扑和直流海缆阻抗变化将直接影响MTDC 系统的潮流分布。对于不同网络拓扑来说,一条直流线路的最小载流量受到与之连接在同一换流站的其他直流线路、换流站额定容量以及整个系统网络拓扑的影响。因此,在海上换流站容量和MTDC 网络拓扑给定的条件下,某一条直流海缆的选型不仅影响自身的载流量,同时也直接影响系统中其他直流海缆的载流量。为了分析直流海缆选型对规划结果的影响,以五端MTDC 系统(见附录A图A13)为例,分析直流海缆选型不同导致阻抗变化对直流输电系统稳定裕度的影响。
附录A 图A14 所示为当图A13 中相关的海上直流电缆的截面,在直流海缆潮流不越限的条件下,由2 500 mm2逐渐缩小时系统稳定裕度的变化趋势。从图A14 可以看出,当直流电缆横截面逐渐减小时,由于直流电缆的阻抗的增加,系统的特征值向左偏移,系统稳定裕度逐步增大。即优化MTDC 系统网络拓扑与线路选型,不仅有助于提高MTDC 系统的经济性,也有助于提高系统的稳定性。
2)MTDC 系统网络拓扑的影响
同样针对五端MTDC 系统,附录A 图A15 罗列了8 种典型的拓扑连接。图中,拓扑PT1、PT2、PT3、PT4为含环形网络的拓扑,拓扑PT5、PT6、PT7、PT8为不含环形网络的拓扑。针对不同网络拓扑变化的影响,分别对额定条件下的MTDC 系统稳定裕度和系统投资成本进行了计算,不同拓扑投资成本及相应拓扑下的稳定裕度如图4 所示。

图4 不同拓扑的系统稳定裕度及投资成本Fig.4 System stability margins and investment costs of different topologies
结合图4 和附录A 图A15 可以看出,MTDC 系统采用含有环形结构的网络拓扑相比不含环形结构的网络拓扑,整体具有更高的稳定水平。分析其原因,主要是由于含环形的网络拓扑中有更多的冗余线路,线路中潮流功率更加均匀,有利于系统的稳定。
3)不同PCC 的影响
海上风电功率经不同数量、位置的PCC 以不同容量接入陆上电网时,将对gSCR 呈现不同程度的影响。而陆上电网结构与参数变化也同样影响gSCR 水平。在给定节点2、3 与4 为PCC 且相应的陆上换流站容量取最优方案结果的条件下,对不同条件下的投资成本及gSCR 指标的影响进行分析。
附录A 表A3 所示为不同PCC 接入条件下的14 种组合,计算每种组合下的gSCR 指标和系统总投资成本Ccost如图5 所示。图5 中,分别以计算结果中最大的gSCR 结果与Ccost结果为基准(该值取100%)。

图5 不同PCC 接入条件下的Ccost及gSCRFig.5 Ccost and gSCR under different PCC access conditions
结合附录A 表A3 与图5 可以看出:1)PCC 的数量与位置不同,将对MTDC 系统并网方案的投资成本及运行稳定性产生显著的影响;2)整体上来看,从减少MTDC 系统并网投资成本的角度,应尽量减少PCC 的数量;从提高并网稳定性的角度,应适当增加PCC 的数量。
为了进一步分析PCC 对gSCR 指标的影响,对不同电网参数下的gSCR 指标结果进行对比。为了便于说明,将2 个PCC 之间的阻抗称为直接连接阻抗;非PCC 节点与PCC 之间的阻抗称为间接连接阻抗。当直接连接阻抗与间接连接阻抗发生变化时,计算得到的gSCR 如图6 所示。
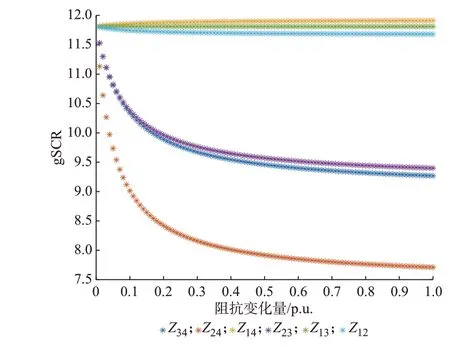
图6 gSCR 随着交流系统阻抗增加的变化Fig.6 Variation of gSCR with AC system impedance increasement
从图6 可以看出:1)直接连接阻抗(Z23、Z24与Z34)的变化对gSCR 影响显著,而间接连接阻抗(Z12、Z13、Z14)的变化对gSCR 几乎无影响;2)随着直接连接阻抗的增加,gSCR 明显降低。这说明MTDC 系统经多个PCC 接入陆上系统时,从提升交流系统稳定运行的角度,倾向于在待选的PCC 中选取电气联系更紧密的节点作为并网PCC。
5 结语
本文针对海上风电经MTDC 系统接入交流电网的优化规划问题,提出了一种兼顾MTDC 系统投资经济性及海上MTDC 系统与陆上交流电网运行稳定性影响的综合优化模型。相关分析与计算得到的主要结论如下:
1)基于海上MTDC 系统灵活多变的网络形式,提出了一种MTDC 系统拓扑连接矩阵,有助于直观地用于MTDC 系统的小信号模型构建及MTDC 系统直流海缆成本计算,对进行海上风电经MTDC 系统接入交流电网的多方案优化具有有效性;
2)本文构建的包含MTDC 系统单位稳定裕度成本和gSCR 的综合目标指标及其计算方法,有助于在海上风电经MTDC 系统并网规划中保证投资经济性的同时,提高MTDC 系统接入交流电网的静态稳定水平;
3)MTDC 规划过程中,优选包含环形结构的网络拓扑,综合陆上电网条件优化PCC 数量与位置,能够有效改善系统的静态稳定水平。
本文仅考虑了主从控制策略下的海上MTDC系统规划问题,后续研究可结合下垂控制策略,进一步探讨不同运行场景下、不同控制策略的转换对海上风电经MTDC 系统并网规划的影响。
本文在研究过程中得到上海绿色能源并网工程技术研究中心帮助,特此感谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
