钠钾流量计在流致振动作用下的疲劳寿命分析
2022-10-17张振国吴菱艳李小畅田瑞峰
姜 超 张振国吴菱艳 李小畅 田瑞峰
(1.中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610000;2.黑龙江省核动力装置性能与设备重点实验室,黑龙江 哈尔滨 150001)
0 引言
从20世纪中叶开始,各国的学者对流体绕流诱发的流致振动现象就展开大规模研究工作,已有大量研究成果。随着反应堆运行堆年数的增加,流致振动问题在核电领域受到越来越广泛的关注。钠冷快堆以液态钠为冷却剂,堆内结构长期处于流致振动的交变载荷下,会引起结构材料的疲劳损伤,进而可能造成严重核事故,因此对反应堆堆内结构进行“流致振动—寿命分析”在核工程领域,有着重要的意义和应用前景。
1 疲劳和疲劳寿命分析理论
1.1 基本概念
“疲劳”是指材料在循环载荷作用下的损伤和破坏。“疲劳寿命”是指结构材料直至破坏所作用的循环载荷的次数或时间。
本文在给定的计算工况下,流致振动对流量计产生的载荷为等幅循环载荷,而且结构的应力应变数值较小,最大振幅数量级为10mm,可以将材料的塑性应变忽略。故本文采用单向流固耦合方法进行数值计算,采用名义应力法来估算流致振动对流量计疲劳寿命的影响。
1.2 S-N曲线
为了估算疲劳寿命,需建立载荷与寿命之间的数值关系,即S-N曲线,如图1所示。
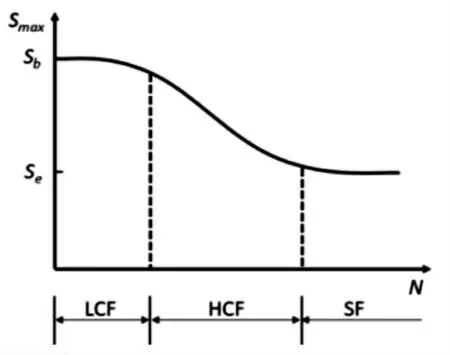
图1 典型S-N曲线
研究人员进行大量研究,提出诸多S-N曲线模型,其中最基本的形式是幂函数公式:

式中,α和C为材料常数。
本文主要关注钠钾流量计流致振动所造成的循环载荷对流量计产生的疲劳影响,预测其疲劳寿命。由于载荷的循环次数较高,循环载荷数值较低,所以本文将主要采用S-N曲线上HCF和SF区段。目前,有很多研究给出了描述材料S-N曲线的数学模型,这些模型在应力循环次数范围内能够反映材料的疲劳寿命,但大多数模型无法对高周疲劳寿命和超高周疲劳寿命(亚疲劳寿命)进行估算。
王明珠参考吴富强的全寿命曲线模型,提出了一种新的疲劳寿命曲线模型,如图2所示。

图2 王明珠提出的S-N曲线模型
当应力等于抗拉强度S时,循环应力作用1/4个周期时就会发生疲劳损伤,疲劳寿命N=1/4;当应力小于理论疲劳极限S时,疲劳寿命N=∞,材料不发生疲劳损伤。该寿命曲线模型可表示为:
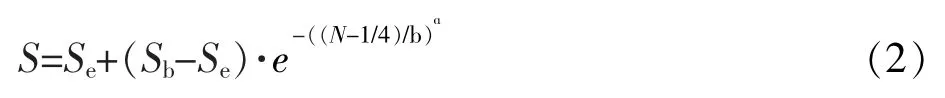
式中,S为理论疲劳极限;S为极限抗拉强度;a和b为材料常数。
根据50钢的金属疲劳试验结果,本文采用非线性参数拟合方法得到S-N曲线模型参数,如表1所示。

表1 50#钢的S-N曲线模型参数
1.3 疲劳累积损伤理论
本文所采用的疲劳累积损伤理论的数学表达形式如下:
(1)n个循环载荷造成的损伤:

式中,N为当前载荷水平S下的疲劳寿命。
(2)临界疲劳损伤D:
当累积疲劳损伤值D=1时,可认为疲劳破坏发生,即D=1。
2 流固耦合方程
流固耦合问题是计算流体力学(CFD)与计算固体力学(CSM)交叉产生的一门学科分支。
固体控制方程式为:


应力τ、位移d守恒方程式为:


3 物理模型
3.1 几何模型
根据流量计整体结构示意图以及流量计结构的相关尺寸,在SolidWorks软件中建立相应的固体域物理模型,如图3所示。

图3 固体结构示意图
敏感体组件由中间的圆柱段和两端的圆锥体组成,敏感体组件直径为31mm,长为146.5mm;支撑件是连接敏感体与管道壳体的结构件,其直径为20mm;壳体组件是内径为50mm的空心圆管,管壁厚1.5mm。流量计的安装方式有两种:水平安装和垂直安装。其对应的重力方向也不同,会对结构力学计算产生影响。因此,本文设置了两种不同的重力方向分别进行疲劳计算。
3.2 网格模型
分别对流体域和固体域划分网格,并对流体域近壁面区域和固体域支撑件结构处的网格进行加密。经网格无关性验证计算,最终流体域网格数量约73万,网格质量总体在0.36g以上;固体域网格数量约15万,网格质量总体在0.54g以上,满足计算要求。
4 流致振动及疲劳寿命计算
流量计的入口流速为1.863m/s。工作条件下液态NaK-78合金的密度为820.3kg/m,动力黏度为2×10kg/(m·s)。
4.1 时间步长的选取
流量计敏感体组件在工质流动中,其下游会出现漩涡,这些漩涡周期性地交替脱落,并对敏感体组件及其支撑件产生交变作用力,形成交变负荷。应力的频率与漩涡脱落频率f一致:

式中,Sr为斯特劳哈尔数。
罗斯柯(A.Roshko)1954年的实验结果表明,当Re大于1 000时,Sr可近似等于0.21。
在本研究中,流场雷诺数Re的取值范围为3.8×105~5.2×10,因此斯特劳哈尔数Sr取0.21。根据公式(7)可估算得漩涡脱落的频率f约为13Hz,即周期T为0.077s。Sr与Re关系曲线如图4所示。
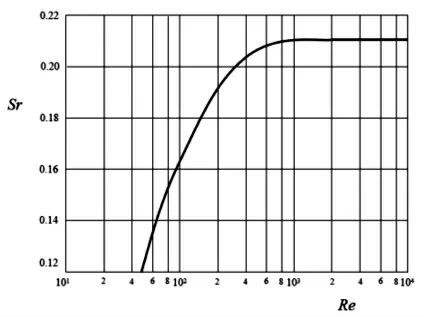
图4 Sr与Re的关系曲线
在瞬态流场的计算中,时间步长Δt取0.001s,瞬态时间步数为2 000步,耦合计算的物理时间为2s。
4.2 结构应力计算
固体结构力学计算可得到应力分布、应力幅以及应力循环周期。在疲劳寿命分析中,将可能产生较大应力的点称为“热点”,“热点”处的交变应力称为“热点应力”。在本研究中,结构关于xOy平面对称,因此选取了如图5所示的6个“热点”进行应力分析。

图5 “热点”的位置分布
本文在ANSYS Workbench平台上进行流固耦合计算,通过流固耦合面将流场的压力计算结果导入Transient Structural模块进行结构力学计算,并对确定的六个“热点”进行瞬态应力分析,可得到如图6所示的在不同安装方式下各个“热点”在1.3~2.0s区间的应力谱,可知其应力的交变频率f为11 Hz。从各应力谱曲线中提取的各个“热点”的应力参量如表2所示。
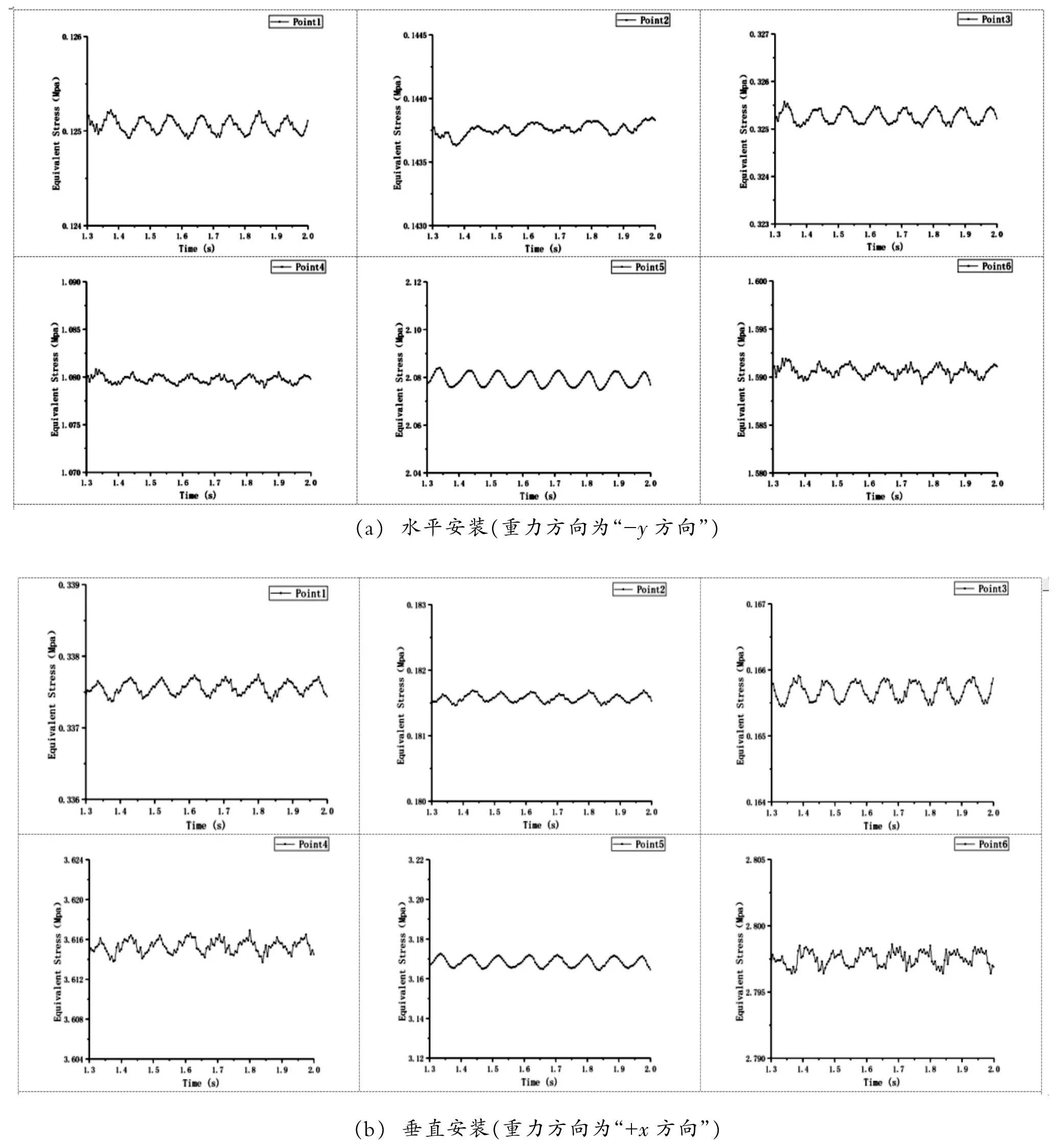
图6 各个“热点”在1.3~2.0s区间的应力谱

表2 各个“热点”的应力参数和疲劳寿命模拟结果
4.3 疲劳寿命计算
疲劳按应力循环作用周期分为高周疲劳和低周疲劳。高周疲劳可用应力疲劳分析法。低周疲劳通常伴随材料的塑性变形,一般采用应变疲劳分析法。考虑到本研究仅涉及高周疲劳问题,故采用应力疲劳分析。
考虑到偶然因素对疲劳寿命的影响,极限寿命一般为使用寿命的倍数,这个倍数被称为疲劳设计安全系数DFF,公式表示为:

式中,Life为极限寿命;Life为使用寿命。
疲劳寿命的计算采用如下公式:

式中,Life为设计寿命;D为设计寿命下的疲劳损伤;DFF为疲劳设计安全系数。
本文研究的流致振动造成的振动载荷是恒定振幅循环载荷,因此在计算中将忽略冲击过载对结构疲劳寿命的影响。根据美国船级社《近海结构物疲劳分析规范》中的内容,可将DFF取值为2。
设计寿命N可按下式计算:

式中,f为应力循环频率;Life为设计寿命。
借助ANSYS Workbench平台开展静力学分析,并采用Gerber平均应力修正法得到各个“热点”在设计寿命N下累积的设计疲劳损伤值D,再由公式(10)计算得到各点的疲劳寿命Life,如表2所示。两种安装方式下流量计的疲劳寿命分析结果对比如图7所示。
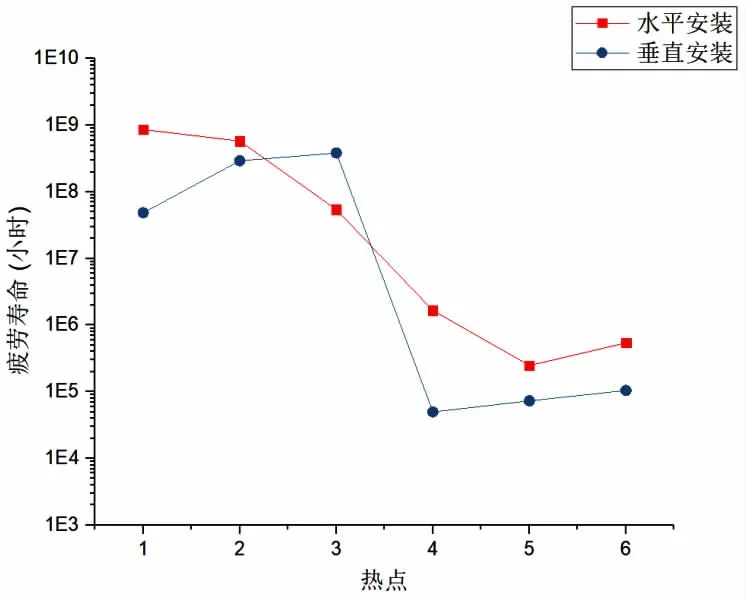
图7 两种安装方式下疲劳寿命值的比较
5 结语
本文的研究方法可以用于流固耦合作用导致的结构及装置振动的疲劳寿命预测,适用于流致振动作用下的高周疲劳计算。本文采用单向流固耦合的方法进行求解,对钠钾流量计在流致振动作用下的疲劳寿命进行了数值分析,结论如下:
(1)流量计水平安装时,疲劳薄弱点为“热点5”,其疲劳寿命为2.48×10h;流量计垂直安装时,疲劳薄弱点为“热点4”,其疲劳寿命为4.98×10h,均满足3×10h疲劳寿命的要求。
(2)在与流场力的耦合作用下,不同方向的静态载荷(重力)会对结构的应力分布产生显著影响,最大交变应力出现的位置也不同,对应其疲劳薄弱点也会出现在流量计不同位置。
(3)流量计在水平安装方式下的疲劳寿命比在垂直安装方式下更大,流量计水平安装有利于延长流量计的疲劳寿命。
(4)在两种安装方式下,流量计的疲劳薄弱部位均在流量计支撑件与壳体相连处。
