放手让学生自主探究打造高品质生本课堂——以“无理方程的解法”的复习为例

苏灿强

福建省安溪第一中学 362400

复习“无理方程的解法”时，某教师精心挑选了两道典型例题，与学生共同探讨解题方法，取得了较好的教学效果，现将教学过程呈现给大家，供借鉴！

教学片段

例1求方程=xy的实数解.

师：不计算，先猜一猜方程的根是什么.

生1：x=y=2.

师：还有其他根吗？

生1：这个猜不出来，应该要计算了.

师：确实，猜出来的结果也不具有说服力，那么例1该如何求解呢？

接下来教师鼓励学生独立完成计算，几分钟后，学生依然一筹莫展，于是教师只好将自己的解题过程讲授给学生.

教师给出答案后，并没有继续探究，而是预留时间让学生理解、消化.几分钟后，教师准备探究后面的问题时，有学生兴奋地说道：“老师，我有了新解法.”

师：说一说，你是如何求解的呢？

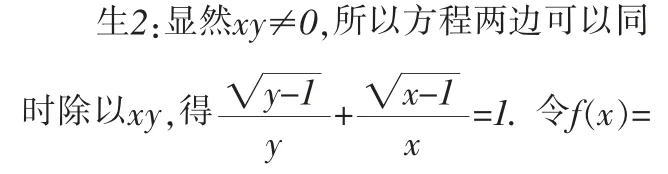
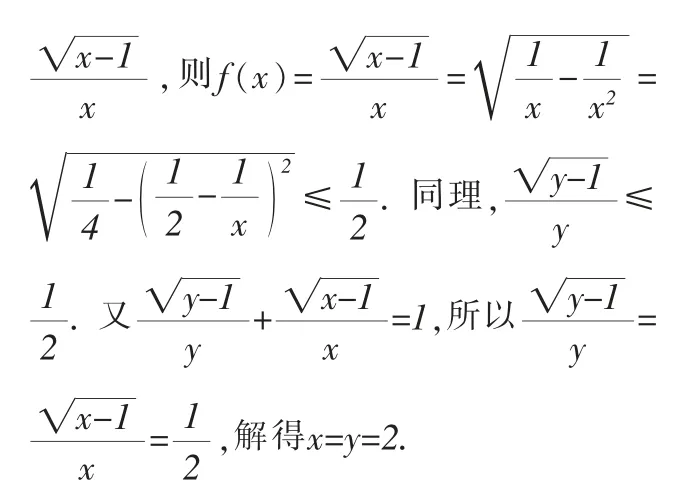
师：不错，非常漂亮的解法，你是怎么想到的呢？

生2：最初我也尝试通过解方程的思路来求解，但是计算量太大，所以就没有继续做下去.我又观察了原式，从结构特点出发，同时除以xy，得到=1，对两个变量分开研究，得到了最后的答案.

师：敢于尝试、勇于探索，非常好.解题时，大家要有打破常规的精神，勇于实践，这样你会收获更多.

生3：我也发现了新解法.由于根号里的表达式为x-1和y-1，联想到sec2α-1=tan2α，可进行如下变换：令x=sec2α，y=sec2β，其中0＜α，β＜，从而x-1=tan2α，y-1=tan2β，有sinβcosβ+sinαcosα=1，即sin2β+sin2α=2，从而sin2β=1，sin2α=1，α=β=，因此x=y=2.

师：结合无理方程的对称性，想到了三角换元，从而将代数方程转化为了三角函数问题，跨领域联想，非常有创意.

点评：在解题过程中，教师预留了充足的时间让学生独立思考，基于大多数学生没有找到有效的解题策略，教师按照预设给出了答案.答案给出后，教师没有急于进行后面问题的讲解，而是预留时间让学生反思回顾，以此促进知识内化.另外，当学生提出解决问题的其他方法时，教师给予机会和时间让学生展示，并及时给出点评，有效地提升了学生的解题信心.

例2解方程：

师：这个是最终的结果吗？是否有其他的解呢？如何进一步说明呢？

师：确实，通过构造函数的方法来求解有一定难度，还有其他解决方案吗？

生5：应该可以通过移项、平方的思路来化简，之前推导椭圆标准方程时就是这样化简的.

师：是一个思路，大家顺着试一试，看看能否求出α呢.

学生积极计算，给出了以下解题方法：

师：很好，这样通过移项、平方的方式将无理方程转化为有理方程，这是解决无理方程的通法.还有其他方法吗？（生不语）

师：联想根式对应的几何意义，你有什么发现吗？（教师预留时间让学生独立思考）

图1

师：这么漂亮的解法你是怎么想到的？

生6的话音刚落，又有学生提出了新想法.

图2

师：非常好.生6和生7充分挖掘了等式中所蕴含的几何背景，把等式中的数量关系巧妙地与直观几何图形联系在了一起，展示了非凡的创造能力.

师：现在回到生4的方案，大家有没有兴趣与我一起将其进行到底呢？调递增.因为x∈，所以当且仅当时，f（x）=4.

图3

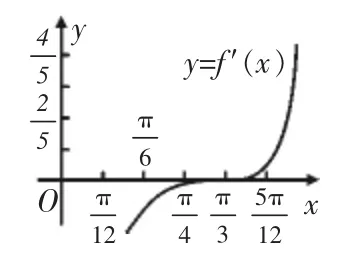
图4

点评：在例2的解决过程中，利用通性通法解决问题后，教师又给学生提供了一定的时间和空间探索其他的解法，以此拓宽学生的视野.然后教师引导学生从二次根式的几何意义出发，创造性地解决了问题.在此过程中，教师为学生搭建了自我展示的舞台，充分暴露了学生的思维过程，让学生在交流展示中丰富了认知，培养了学生良好的思考习惯.另外，教师利用信息技术将学生之前给出的探究方案进行到底，以此通过对比分析让学生理解各种方法的优缺，进一步提高学生的解题能力.

教学思考

众所周知，学生学习能力和思维能力的培养是无法靠灌输实现的，因此，教师将课堂还给了学生，鼓励学生尝试从不同角度思考问题、解决问题.同时，教师要通过适时的启发和引导让学生在自主探究中有所发现、有所收获，以此提高学习能力，落实数学核心素养.现结合教学过程谈几点教学体会：

数学学习是学生自我发现、自我完善的过程.数学学习是学生对数量关系和结构的认识，而这种认识是需要学生自主去发现、去探究、去感悟的，是通过学生自主活动实现的.解题时，教师鼓励学生猜一猜，借助直觉思维理解不同的材料，获得相应的感性认识.接下来，从已有认知和已有经验出发，对相应的数量关系或结构进行逻辑推演，找到了多种解题路径.从以上解题过程可以看出，对数量关系的演绎推理不是短时间内可以完成的，因此需要教师给予足够的时间让学生去探索，鼓励学生用自己的方式解决问题，这样才能展示学生的聪明才智，让学生的学习能力、学习兴趣、学习信心等方面获得较大的提升.教学中，教师只有放手让学生去探索，才能激发学生的参与热情，从而打造出一个生动的、富有活力的数学课堂.

因为学生的经验背景等存在差异，所以学生解题时往往有着不同的表现.在教学过程中，教师要尊重这种差异，因为正是差异的存在，才能使不同的思维在碰撞中迸发出火花，才能呈现出一个丰富多彩的高品质课堂.如从以上两个教学活动可以看出，有的学生利用通性通法求解；有的学生通过构造函数求解；有的学生通过构造三角函数求解；还有的学生通过建构距离模型求解，等等.多样的解题方法呈现出了学生的知识水平、建模能力和思维习惯.这些差异是宝贵的课堂生成性资源，值得去挖掘、去展示.当然，在解题过程中，也会出现一些模糊不清，甚至错误的想法，教师要鼓励学生去追踪溯源，找到问题的症结，以此通过有效启发和指导让学生找到最优的解题方案，以此优化学生认知，发展学生的思维能力.

数学解题教学要摒弃就题论题式的讲解，要从培养创造性人才的角度出发，鼓励学生去发现、去创造.在解题教学中，教师必须深入理解问题，尝试从不同角度去分析和理解问题，以此充分发挥教学的主导功能，引导学生从不同角度审视问题，以此不断进行解题方案的优化与完善，切实提高学生的解题能力，将对学生思维能力的培养落到实处.

总之，在解题教学中，教师要为学生提供一个轻松的“再创造、再发现”的学习环境，鼓励学生去发现、去创造，以此提高学生的学习能力，打造出一个充满激情与灵性的高效数学课堂.