巧借“微专题”提升高三数学二轮复习品质

方丽娜

安徽省亳州市利辛县第七中学 236700

教学现状

经过高三一轮复习后，学生的“双基”得到了巩固和强化，学生的知识网络和方法体系已经基本形成.二轮复习时，部分教师将教学重点放在做题上，片面地认为只有多做题才能提升学生的解题效率和数学成绩.于是，二轮复习时，大多数学生容易沉迷于“题海”，机械地进行模仿和复制，这样不仅浪费了宝贵的复习时间，而且因为重复做题形成了思维定式，遇到问题不去思考，而是机械地套用概念、公式、定理，使思维缺乏灵活性和变通性，学生分析和解决问题的能力未能得到提高，继而影响到二轮复习的效果.另外，二轮复习时为了追求大容量、高速度，部分课堂仍以教师为主导，表面上课堂容量大、方法多、速度快，但是因缺乏学生的思维过程，忽视学生数学思维的训练，使得看上去热热闹闹的课堂变成了教师的“独角戏”，学生的思维能力和解题能力并没有得到明显的提升.

教学分析

纵观历届高考，虽然题目复杂多变，然仔细分析不难发现，其考查的是学生灵活应用基础知识和方法解决问题的能力，考查的是学生的数学核心素养和数学能力.然在二轮复习中，不乏有些师生为了追求新、追求难，使教学发生了偏移，影响了教学效果.为了保证二轮复习的效果，笔者认为，教学中可以选择适当的微专题进行教学，这样既能突出数学本质，又能发展学生的思维.当然，教学中也要改变教学方式和学习方式，充分发挥学生的主体地位，引导学生学会思考、学会学习，从而让学生可以更好地理解数学、应用数学.

笔者通过“以正切为背景的最值问题”这一微专题为例，阐述了自己对二轮复习的几点认识，供参考.

教学片段

片段1：探究实例，夯实基础

师：思考一下，如何求解例1？（教师用PPT给出例1，并让学生独立思考）

例1在斜△ABC中，求证：tanA+tanB+tanC=tanAtanBtanC.

生1：由A+B+C=π，得tanA=tan［π-（B+C）］=-，展开得tanA+tanB+tanC=tanAtanBtanC.

设计意图：例1为教材习题，这样以学生熟悉的习题为引例，让学生更有亲切感，更易于激发学生的参与积极性.本题求解时利用“A+B+C=π”这一等量关系，通过两角和的正切公式探究tanA，tanB，tanC三者的等量关系式，便于学生理解和接受.

师：例1求解大家都完成得非常好，现在我们一起来看一下例2.（教师继续给出问题）

例2在锐角三角形ABC中，已知sinC=4cosAcosB，求tanAtanB的最大值.

同样，例2求解依然以生为主，教师引导学生将已知转化为三个角的正切关系.

生2：由sinC=4cosAcosB 得sin（A+B）=4cosAcosB，即sinAcosB+cosAsinB=4cosAcosB.由C∈（0，π），可知sinC≠0，则cosAcosB≠0.于是上述等式左、右两边同时除以cosAcosB，得tanA+tanB=4.又△ABC为锐角三角形，故tanA ＞0，tanB＞0，则tanA+tanB≥，所以当tanA=tanB=2时，tanAtanB取得最大值4，此时tanC=，符合题意.

设计意图：借助简单的、易于理解的问题帮助学生回顾三角形内角的正弦、余弦转化为正切的基本思路，以及二元求最值的基本方法.

师：在例2的条件下，能否转化为其他的最值问题呢？（生深思）

生3：求tanA+tanB+tanC的最小值.

教师让学生独立求解，并展示了求解过程，最终求得tanA+tanB+tanC的最小值为

师：还有其他变式吗？

学生探究的过程这里就不再详细展示了.这样让学生自己尝试变式，目的是让学生明确消元是求三角形内角A，B，C正切表达式最值的基本思路，即通过消元将原问题转化为一元函数求最值问题或转化为二元不等式求最值问题.

师：刚刚研究了三角形中角的正切，接下来还能研究什么呢？

生齐声答：正弦、余弦.

师：很好，三者密不可分，可以相互转化.如何将正切转化为正弦、余弦呢？

师：若是正弦、余弦转化为正切呢？

生7：若已知中是关于正弦、余弦的分式，且分子和分母为齐次式，这样只要分子和分母同时除以角的余弦即可完成转化.

师：说得很好，若是关于正弦、余弦的等式呢？

生齐声答：等式两边同时除以角的余弦.

师：试求sin2A+sin2B的最大值.

设计意图：教师先是强调正弦、余弦、正切三者之间的联系，接下来又让学生回顾如何实现相互转化，为接下来的探究指明了方向.同时，经历以上过程，不仅巩固了知识，而且完成了数学思想的渗透，有利于学生数学学习能力的提升.

片段2：数形结合，深化理解

师：我们知道“数”“形”一家，刚刚的已知条件都是用“数”来表示的，现在我们从“形”出发，又该如何转化呢？（教师用PPT展示例3）

例3如图1所示，在锐角三角形ABC中，CD⊥AB，垂足为D，且AD∶DB=3∶1，求（1）tanA+tanB+tanC的最小值；（2）sin2A+sin2B的最大值.

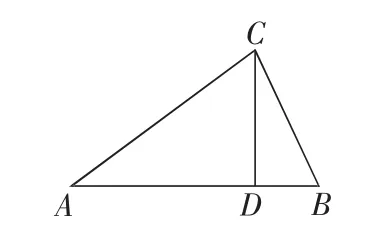
图1

设计意图：转换思路，为后期的拓展延伸做铺垫.学生通过探究可以发现，已知条件AD∶DB=3∶1可以转化为tanB=3tanA，这样通过以上解题思路可以轻松求解.

片段3：有效拓展，抽象方法

师：在三角形中，还有哪些量是值得我们研究的呢？

生8：三角形的边、高、周长、面积等.

师：很好，由例3的已知条件AD∶DB=3∶1，我们可以知道什么呢？

生齐声答：tanB=3tanA.

师：此时三角形的面积是否有最值呢？（生交流）

生8：我认为没有最值，仅已知角的关系式，三角形之间是相似关系，这样只能确定三角形相应的形状，无法确定边、面积、周长等大小.

师：说得非常好，看来如果要探寻三角形面积的最值需要添加一个条件，你们觉得添加什么条件比较合理呢？

生9：可以确定一条边.

师：给出你的完整设计.

生9：在△ABC中，已知tanB=3tanA，且b=1，求S△ABC的最值.

师：很好！大家看一下，添加条件后是否能够求最值了呢？（教师让学生独立思考后，交流展示）

师：很好，运算简单，思路清晰.是否还有其他解题方法呢？

生12：还可以通过建系，将问题转化成点的轨迹问题.

师：具体说一说.

生12：如图2所示，以点A为原点，AB所在直线为x轴建立平面直角坐标系，则点B的坐标为（c，0）.设直线AC为y=kx（k＞0），根据tanB=3tanA，得BC为y=-3k（xc），联立方程后消去k可得x=c.所以点C的轨迹为直线x=c（去除与x轴的交点）.接下来通过设点，结合已知，利用三角形面积公式和基本不等式，求得△ABC面积的最大值为

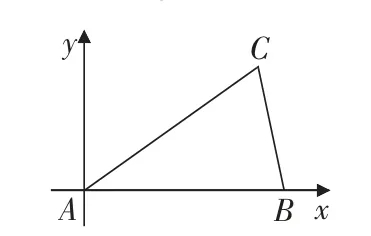
图2

在生12的基础上，学生又给出了不同的建系方法，如以C为原点，CA所在的直线为x轴，建立平面直角坐标系，同样可以求得△ABC面积的最大值.

设计意图：鼓励学生根据已有经验进行多角度探究，并总结归纳出将三角形的正切关系转化为边的关系的常用策略（如将正切转化为正弦、余弦，实现边角关系的转化；构造直角三角形；建立坐标系，转化为点的轨迹问题）.以此既发散了思维，丰富了学生认知，又总结了解决问题的常见策略，有利于学生解题能力的提升.同时，在求最值的过程中，对消元、整体代换、基本不等式、数形结合等数学思想方法的应用，提升了学生数学运算能力.

片段4：更换条件，内化知识

接下来，学生又尝试了不同的情况，如更换为a=1，求得当m2=时，△ABC面积的最大值为1；更换为c=1，此时点C的轨迹为直线x=，△ABC的面积无最值.

师：若在△ABC中，已知tanB=3tanA，且b=1，则△ABC的面积存在最大值.那么在此条件下，△ABC的周长是否存在最大值呢？

生14：还可以用方程的思路求解，令△ABC的周长t=a+c+1，得a=t-c-1，代入2a2+c2=2，这样问题就可以转化为了关于c的方程有正实数解的问题.

设计意图：这样借助“变”进一步深化认知，突出求二元最值的方法，让学生能够灵活应用所学知识和方法解决不同问题.

片段5：自主改编，强化理解

师：刚刚题目中的已知条件为tanB=3tanA，题设信息比较直白，如果换一个方式，转换一个角度，你认为可以如何改编已知条件？

生15：将“tanB=3tanA”改编为“2a2+c2=2b2”.

生16：将“tanB=3tanA”改编为“2sin2A+sin2C=2sin2B”.

师：很好，这些内容刚刚我们已经探究过，是大家熟悉的内容，如果从正弦、余弦定理的角度去改编，你认为可以怎样更换已知条件呢？

生17：a2=b2+c2-2bccosA，代入2a2+c2=2b2，整理得3c=4bcosA.

师：太棒了，还有吗？

生18：还可以从sinBcosA=3sinAcosB入手，转化为sinC=4sinAcosB或c=4acosB.

师：很好，这样转化后问题变得更加新颖别致了.类比上面的方法，是否能够为目标中的“变个身”呢？

师：刚刚我们为已知和目标都找到了许多“新分身”，如果将其重新组合可以得到许多新题，谁来尝试“变一变”？

生19：在△ABC中，已知tanB=3tanA，△ABC的面积等于，求边b的最小值.

师：很好，将已知与目标互换得到了新的问题.还有吗？

师：解题时只要我们把握了数学的本质，就能以不变应万变.

设计意图：这样通过变式改编，将一道题转化为了一类题，不仅让学生理解了解决问题的基本思路和基本策略，而且帮助学生跳出了茫茫的“题海”，有效地提升了教学效率.同时，在转化、类比、总结归纳的过程中，有效提升了学生提出问题、分析问题、解决问题的能力，发展了学生的数学思维.

教学思考

高三数学二轮复习对学生的成绩提升至关重要，教师切勿急于求成而将学生带入“题海”.在二轮复习中，教师设计微专题时可以选择一些切口小、思维宽的问题为切入点，通过由浅入深的逐层深入，挖掘数学本质，探究数学方法，达到“会一题通一类”的效果.微专题的题材可以选择易错点、教学重难点、高考热点等，通过对典型问题的探究更易于学生认识问题的本源，提升其解题能力.

教师在微专题的设计上应注意以下几点：

1.要有明晰的知识和方法框架

为了帮助学生建立完善的认知结构，教师可以通过对关键词的解读和问题的解决帮助学生提炼出解决问题的基本方法，建构知识网络.例如，本专题的教学中，以三角形的正切为背景，将正弦定理、余弦定理、消元、整体代换、函数单调性、基本不等式、数形结合等相关知识与方法串联在了一起，形成了一条巨大的知识脉络，这样通过知识的迁移和拓展有助于学生综合能力的提升.

2.要改变教师的教学方式

在传统教学中，常常以教师为主导，致使教学效率低下.在新课堂上，教师应重视引导、提炼，关注学生的主体地位，引导学生主动揭开问题的面纱，使学生由被动“接受”转化为主动“建构”，领悟数学的本质，形成数学品质和数学能力.

教学中，教师要跳出“一节一知识”的束缚，学会从整体上把握数学课程，突出教学主线，同时通过引导和追问让学生将分散的知识点串联起来，构建和完善认知.另外，要引导学生从多角度去分析和解决问题，感悟解决问题的策略与方法，体验基本方法的应用，感受知识的价值，提升学生数学学习的信心.

3.要改变学生的学习方式

在传统教学模式的影响下，很多学生已经习惯了“听”和“记”，缺乏独立思考和主动建构的能力，因此学习中显得被动、消极.为了改变这一现状，课堂上应多为学生创造一些机会去探究、去发现、去归纳总结，从而在探究的过程中发现并提出问题，在发现的过程中学会分析，在归纳总结中学会抽象，以此优化认知，提升实际解决问题的能力.

在本节微专题教学中，学生是课堂的主角，整个过程关注学生自主探究能力的提升.例如，解决了三个角正切值有关的问题后，教师并没有引入新的问题进行“题海”强化，而是转换角度，引导学生探究三角形的其他元素（如面积、周长）等，通过添加不同条件，应用不同方法揭示问题的本质，不仅深化了学生认知，而且拓展了学生的知识面，拓宽了学生的视野，让学生的数学分析、数学运算等素养得到了真正的发展.

总之，二轮复习时教师不仅要关注学生解决问题能力的提升，还要关注学生自主探究能力的发展.可借助一题多变、一题多解揭示数学的本质，发展学生的数学思维，提升学生的数学素养.