借助“推理”助力数学应用意识的养成
——以“草原上的蒙古包”的教学为例
2022-10-16李冰文菊
李 冰 文 菊
四川省宜宾市教育科学研究所 644000 四川省宜宾市人民路小学校 644000
数学课程标准指出:“初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识。”基于此,教师在日常教学中需要帮助学生认识到现实生活中蕴藏着大量的数学信息、数学在现实世界中有着广泛的应用;面对实际问题时,能主动尝试从数学的角度运用所学知识和方法寻求解决问题的策略。我们选用《数学文化读本》上的内容,在教学过程中借助推理来探究真相,助力学生应用意识的养成。
“草原上的蒙古包”是《数学文化读本》六年级的教学内容。本课需要学生探究蒙古包的设计原理,并了解圆柱形物体的特征。同时学生通过推理、分析,将数学知识与生活实际相联系,感受数学知识在建筑中的广泛运用,逐步养成应用意识。本课看似简单却蕴含着许多数学知识,如何取舍本课知识点,确定教学重难点,需要教师把握住小学阶段对“图形与几何”这一板块知识的具体要求。我们将本课教学重点确定为:探究体积相同的立体图形中表面积最小、容积最大的圆柱。同时,立足作为《国家课程》相关知识点的延伸和补充这一要求,本课侧重于小学数学核心素养中推理能力以及应用意识的培养。我们创编故事情节,使学生在这个过程中学会自主地用数学眼光和数学思维去分析生活中的实际问题,进而培养学生的应用意识和应用能力。
一、巧用数学文化,发掘实际问题
数学文化主要是指通过人们实际参与各种数学活动,包括数学研究与数学学习,逐步形成的一些特殊的行为方式、思维方法与价值观念,而《数学文化读本》从数学文化的角度引入的“草原上的蒙古包”这一教学内容,就是将生活实际与数学应用相结合。
片段一:
出示故事人物:博士、天天、波波、妮妮和万事通,以及大草原的美丽图片。
师:欢迎同学们加入有趣的数学文化之旅,今天我们将和其他小伙伴一起跟随博士开启一段探寻内蒙古大草原的旅程。
师:一路上,大家都沉醉在大草原的辽阔美景之中,忽然妮妮指着远方小小的白点问,这是什么啊?
生1:蒙古包。
师:什么是蒙古包?
生2:蒙古包就是蒙古族人民居住的房子。
师:那关于蒙古族,你们有什么了解呢?
……
师:大家对蒙古族的了解真不少,这节课我们就一起走近草原上的蒙古包。
数学文化的建设是一个潜移默化的过程,教师传授给学生的不仅是知识和技能,更重要的是在教学中体现思维,给人一定的智慧。这里开门见山地交代故事起因和故事人物。通过学生对蒙古族的民族特点及文化特色的介绍,来了解蒙古包建筑的文化背景,也为后面探究实际问题埋下伏笔。
二、经历自主推理,养成应用意识
数学应用意识的培养要求教师在教学的过程中向学生强调数学的存在价值。通过教师提出有价值的问题,或引导学生发现问题,改变学生在数学知识学习中的被动状态,激励学生更加积极主动地思考和学习。故事情节环环相扣,学生不自觉地跟随情节经历一次又一次的合情推理,在潜移默化中养成应用意识。
设计流程:

图1
(一)推理一:探究底面周长一定,圆柱体空间最大。
片段二:
1.引导学生提出问题。
课件展示一个蒙古包。
师:面对蒙古包,你有什么疑问吗?
生3:我想知道为什么蒙古包会是这样的形状呢?
师:是什么形状?
生4:就是一个圆柱和一个圆锥。
教师根据学生回答画出由一个圆柱和一个圆锥组成的简易蒙古包。
2.探究计算。
根据情节,播放幻灯片。
师:跟大家一样,天天也在问博士为什么蒙古包要建成这种形状。
博士神秘一笑,说道:这样吧,今天我们就在这里安营扎寨,住下来慢慢了解。妮妮一听要自己动手搭房子,特别兴奋地说:好耶,我要住宽敞的大房子。博士说:好啊,你们先设计,我到旁边部落去找点材料。
师:我们和小伙伴们一起设计吧!妮妮想要住最宽敞的房子,你能给她什么建议呢?
生5:肯定是圆柱体啊!
师:为什么?
生5:因为蒙古包都是圆柱体的。
师:如果从数学的角度来思考,为什么必须是圆柱体的蒙古包呢?
师:温馨提示,大家可以分底面和侧面两个部分来分析。
生6:哦,我知道了。看底面,如果是周长一样的长方形、正方形和圆形,那么圆形的面积最大。
师:认同他的观点吗?同意他的观点的举手……
可妮妮却半信半疑,怎么办?
师:其实在数学上,最具说服力的还是数据,这样,我们来填表(见表1),用里面的数据说明你的观点。
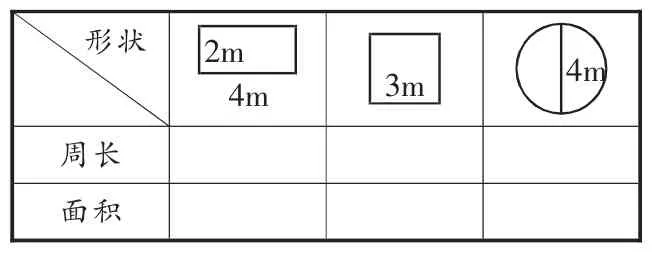
表1
学生完成表格,并说明观点。
妮妮却说:面积大又不能代表空间大!
生7:我们得算体积才知道。
师:体积怎么算?
生7:底面积×高。
师:好,现在我们就把这几个长方形、正方形和圆形作为底面来围,如果材料高3 米,它们的体积分别是多少?
学生独立完成,并指明回答。
师:结合这些数据,你准备怎么说服妮妮?
生8:周长一定时,圆的面积最大;底面周长和高一定时,圆柱体的体积最大。
教师引导学生自主提出问题,并围绕问题,跟随故事情节,“逼”出圆柱体。用帮助故事人物的情境,迫使学生去计算探究“周长一定,圆形面积最大”“底面周长和高一定,圆柱体体积最大”。
(二)推理二:探究底面积和高一定,圆柱侧面积最小。
片段三:
妮妮听了大家的结论,说:好,12m2够我们5 个人住了,我们就搭圆柱形。
波波不满地说:你倒是宽敞了,需要的材料不就多了吗?这个部落那么小,博士能找到的材料肯定不多。
妮妮委屈地说:难道围成圆柱体需要的材料就最多吗?
师:同学们,你们认为呢?
生……
生9:我觉得材料都一样多。
生10:我觉得底面是正方形的用的材料少一点。
生11:哦,这就是刚才我们还没讨论的侧面的问题。
师:是的。但,看样子大家都不太确定。怎么办?
生11:去算一算就知道了!
师:算什么?
生11:算侧面积啊!
师:好难算啊!一定要算出侧面积才能比出材料多少吗?
……
师:侧面积是怎么算的?
生11:底面周长×高。
师:对的,这里材料高度都一样,那么我们就只需要算什么?
生(齐):底面周长。
师:好,那我们分头行动,分组去算长方形、正方形和圆形的周长吧!
小组合作学习(如图2)。

图2
学生汇报。
分组展示每种形状的周长。
生12:r2=12÷3=4,r=2m,C=2×2×3=12m。
生13:12=1×12=2×6=3×4,①(1+12)×2=26m,②(2+6)×2=16m,③(3+4)×2=14m。
生14:12=a×a,①3×3=9m2,②4×4=16m2,③3.5×3.5=12.25m2,3.5×4=14m。
师:你为什么先去找 了32、42,最后确定3.52呢?
生14:我不知道哪个数的平方是12,但知道32比12 小,42比12 大,所以就取了3.52。
师:真棒,为你点赞,开平方是中学的内容,现在你们能推导出3.52,已经很棒了!
听了大家的意见,波波嘀咕道:周长少,又不是材料少!
师:看来还是得算一算侧面积。
全班一起计算侧面积。
师:通过刚才两次计算,我们来梳理一下发现,好说服波波。
生15:面积一定时,圆的周长最小;底面积和高一定时,圆柱体的侧面积最小。
此处是本课的教学难点,也是重点,根据学生的认知基础,他们是无法通过面积计算出正方形的边长的,而且长方形的情况也有多种,于是我们将难度进行了三次分解:一是将三种形状分给几个组,每个组只计算一种情况;二是将直接计算侧面积分解成先算底面周长,然后计算侧面积;三是将长方形的多种情况确定在整数范围,同时引导学生不直接计算正方形的边长,而是用已经知道的平方数推导出近似值。分解的目的是让学生在能力范围内去自主探究出结论,而不是教师直接讲解。
(三)推理三:类比推理生活中其他的圆柱形物体。
片段四:
小伙伴们正讨论激烈,博士找到材料回来了,问:你们设计好了吗?
学生告知了博士他们总结出的圆柱体的特征:空间大、用材少。
博士会心地笑了。
波波恍然大悟道:我知道,原来生活中的水管就是利用圆柱体这个特征设计的物品。(这样的物品还有吗?)
生16:水桶。
生17:笔筒。
博士满意地点点头,说道:其实不仅人类有这样的智慧,植物也同样有……看课件。(介绍植物的枝干、根茎)
通过计算、分析得到蒙古包主体搭建成圆柱体的缘由后,接着让学生用迁移推理的方法去探究蒙古包圆锥形顶部的原理,也就水到渠成了。
(四)推理四:探究蒙古包圆锥形顶部的原理。
片段五:
师:接下来,博士就带着小伙伴们动起手来,不一会就将蒙古包主体搭建好了。
天天又问道:顶部该怎么搭呢?有什么好的建议吗?
同桌交流推理顶部构造的理由,并汇报。(不积雨雪、牢固)
通过对蒙古包外形特征的总结,让学生感受数学知识在生活中的广泛运用。而将圆柱体的特征延伸到生活中,目的在于让学生知道生活中是如何运用这些特征的,通过寻找数学与生活的联系,培养学生的应用意识。
推理全过程中,学生会计算正方形、长方形、圆形的周长、面积,正方体、长方体和圆柱的体积,并进行多次比较。在这一过程中,学生经历了一次次的推理,进行了层次分明、目的明确的练习;巧妙地突破了本课的重难点,培养了推理能力,认识到现实生活中蕴藏着大量的数学信息,养成了应用意识。
三、拓宽观察视野,提出延伸问题
问题是引发学生思考的根本,通过引导学生提出新的实际问题,既是让知识走向深入,更是促使学生主动尝试从数学的角度,运用所学知识和方法寻求解决问题的策略,同时也是养成学生应用意识的有效策略。
片段六:
听完介绍,当大家唏嘘不已时,万事通也感叹:这趟草原之行收获可真不少!你有收获吗?
博士又问:那你们还有什么疑问吗?
生(齐):为什么我们这些地方的房子不修成圆柱形呢?
师:没关系,我们的草原之行还没有结束,带着你的疑问我们下节课继续旅程。
本节课中,教师从学生已有的知识经验出发,精心组织教学内容,设计故事情节和丰富数学活动,让学生在故事情节中提出猜想,经过一次又一次的推理去验证自己的猜想,积累了数学活动经验,养成了数学应用意识。
