决策蕴涵与可变决策蕴涵上的推理规则研究

薛东前，翟岩慧,2+，张少霞，李德玉,2，徐伟华

1.山西大学 计算机与信息技术学院，太原030006

2.山西大学 计算智能与中文信息处理教育部重点实验室，太原030006

3.西南大学 人工智能学院，重庆400715

形式概念分析（formal concept analysis）是德国Wille 教授1982 年提出的从形式背景建立概念格来进行数据分析的有效数学工具，其核心概念为形式背景、形式概念与概念格。形式概念分析通过概念格所展现出的概念之间的特化与泛化关系，揭示了数据表的内在结构，发现了对象与属性之间的依赖关系。目前，形式概念分析已被广泛地研究，并应用到关联分析、推荐系统、属性约简以及基于概念的认知学习等相关领域中。

形式概念分析对知识获取的研究就是对蕴涵的研究。由于形式背景中得到的蕴涵数量往往很庞大，Qu等提出了决策蕴涵。决策蕴涵是在决策情形下的蕴涵，反映了条件属性和决策属性间的决策关系。Zhai等从语义方面给出了决策蕴涵的闭包、一致闭包等相关概念，并对-推理规则的完备性进行了讨论；提出了合并推理规则，证明了扩增推理规则与合并推理规则相对于决策蕴涵语义层面的完备性，即给定一个完备集，可以通过扩增推理规则和合并推理规则从完备集中推导出对应的封闭集。在此基础上，贾楠等提出了新的推理规则：合并推理规则。相比于合并推理规则，合并推理规则形式上更加简洁，并证明了合并推理规则是合理的，并且该推理规则与扩增推理规则组成的推理规则集是完备且无冗余的。

上文研究仅仅考虑了确定条件下属性蕴涵，针对不确定条件的情况，Zaki等研究了关联规则的语义，Balcázar提出了标准冗余、普通冗余和基于闭包冗余等概念，并且在此基础上提出了基于普通冗余的推理规则以及基于闭包冗余的推理规则。基于这些研究，Zhai等在不精确条件下对决策蕴涵进行了拓展，提出了可变决策蕴涵，从逻辑层面研究了可变决策蕴涵的语义和语构特征。在语构方面，文献[22]提出了四条推理规则，并且证明了其中三条推理规则“有效度收缩推理规则”“有效度提升推理规则”和“置空推理规则”相对于可变决策蕴涵的语义是合理的和完备的。另外，Zhang等考虑了其他知识表示形式，如概念规则和粒规则，讨论了这些知识表示形式与决策蕴涵之间的关系。Zhai等进一步研究了模糊决策蕴涵，从逻辑角度研究了模糊决策蕴涵的语义特征和语构特征。

虽然不同框架提出了不同类型的决策蕴涵，但是并没有对不同类型的决策蕴涵进行比较性的研究。本文基于可变决策蕴涵，提出了受限可变决策蕴涵，并从语构层面研究了受限可变决策蕴涵和决策蕴涵在推理规则上的关系，并从语义层面为语构上的区别提供了解释，同时对受限可变决策蕴涵和决策蕴涵在知识推理能力强弱等方面进行了探讨。

1 基本概念及性质

1.1 决策蕴涵逻辑

决策蕴涵主要分为数据层面与逻辑层面上的研究。本节主要介绍了决策蕴涵逻辑层面上的研究，分为语义研究和语构研究。

决策蕴涵的语构方面主要研究推理规则的合理性、完备性和无冗余性。文献[17]提出两条推理规则。

扩增推理规则：

合并推理规则：

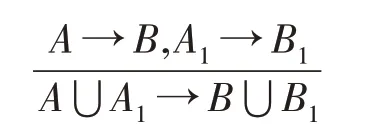
文献[17]进一步证明了扩增推理规则和合并推理规则的合理性、完备性以及无冗余性。

1.2 可变决策蕴涵逻辑

设为完备格，可变决策蕴涵的形式为(→,)，其中(→)为决策蕴涵，∈称为决策蕴涵的有效度。

设为完备格，⊆(⋃)。定义可变决策蕴涵函数为α:2×2→，满足对于任意,∈2，若⊆，则α(,)≥α(,)。

几种可变决策蕴涵函数定义如下。

令=(,,,)为决策背景T={g⋃g|∈}⊆(⋃)，⊆，⊆。

（1）设=[0,1]，则置信度是可变决策蕴涵函数：

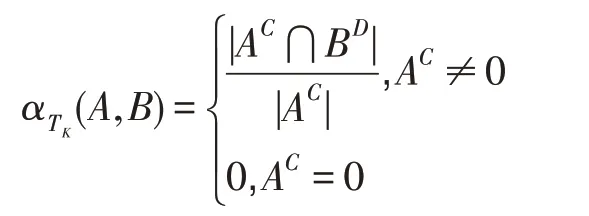
（2）设=[0,1]，则支持度是可变决策蕴涵函数：

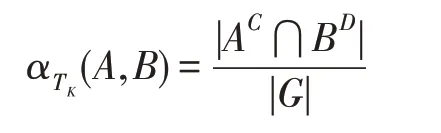
（3）设=[0,1]×[0,1]，则置信度和支持度是可变决策蕴涵函数：

设L为可变决策蕴涵集，定义可变决策蕴涵函数(,)=∨{y|(→B,y)∈L且⊆B}。

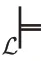
设L为可变决策蕴涵集，定义：

可变决策蕴涵的语构方面主要是研究推理规则的合理性、完备性和无冗余性。文献[22]提出四条推理规则。

有效度收缩推理规则：

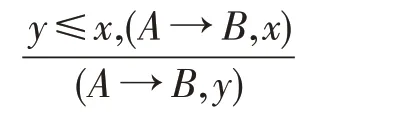
有效度提升推理规则：

置空推理规则：

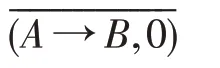
后件收缩推理规则：

文献[22]证明了有效度收缩推理规则、有效度提升推理规则和置空推理规则的合理性、完备性以及无冗余性。

2 受限可变决策蕴涵

2.1 受限可变决策蕴涵的语义

需要将可变决策蕴涵的不确定性剥离，才能对可变决策蕴涵和决策蕴涵进行比较，为此，本文首先将有效度限制到集合={0,1}。

令={0,1}，∈，称可变决策蕴涵(→,)为受限可变决策蕴涵。

由定义9 可知，若有效度为1，可变决策蕴涵(→,1) 成立；若有效度为0，可变决策蕴涵(→,0)不成立。为了防止混淆，将受限可变决策蕴涵集记为L。

根据定义5，受限可变决策蕴涵函数定义为：

需要注意的是，命题3 仅仅在剥离不确定性情况下成立，对于一般的可变决策蕴涵不成立，如例2所示。

令L={(→,(1,0.5)),(→,(0.5,1))}，=[0,1]×[0,1]。应用有效度提升推理规则到L可得(→,(1,1))，即有L⊢(→,(1,1))。然而，L中并不存在{}⊆′满足(→′,(1,1))⊆L。

由例2 可以看出，命题3 对于可变决策蕴涵不成立是源于真值结构的不可比性或非链性。换句话说，若为链，则命题3 对可变决策蕴涵成立。

令=[0,1]，L 为可变决策蕴涵，则L⊢(→,1)当且仅当存在⊆′满足(→′,1)∈L。

2.2 受限可变决策蕴涵的语构

本节将可变决策蕴涵上的推理规则应用于受限可变决策蕴涵。

通过分析可知，应用有效度收缩推理规则到(→,1)只能推导出(→,1)，因此该推理规则对于受限可变决策蕴涵失效。应用有效度提升推理规则可得到以下推理规则。

有效度提升推理规则1：

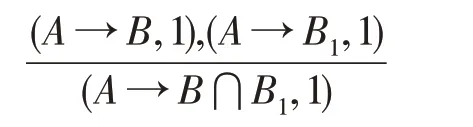
有效度提升推理规则2：

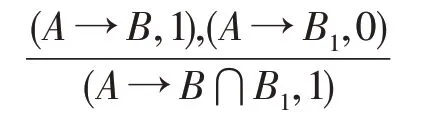
对于(→,0)和(→,0)，应用有效度提升推理规则只能得到(→⋂,0)，因此，有效度提升推理规则在这种情况失效。当可变决策蕴涵的有效度为0 时，该可变决策蕴涵不成立，因此不是有效的决策知识。

可以看出，有效度提升推理规则1 的作用是缩减成立的可变决策蕴涵(→,1)或(→,1)的后件为⋂；有效度提升推理规则2 的作用是缩减(→,1)的后件。由有效度提升推理规则1 和有效度提升推理规则2 可知，无论(→,1)的有效度等于1 还是0 都可以得出(→⋂,1)，因此，可变决策蕴涵(→⋂,1)的成立与(→,1)的有效度没有关系；换句话说，有效度提升推理规则1 和有效度提升推理规则2 可以合并为一条推理规则——-有效度提升推理规则：

最后，应用后件收缩推理规则可得-后件收缩推理规则：

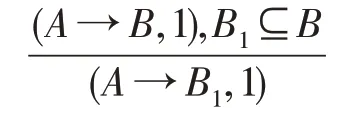
命题5 说明-有效度提升推理规则和-后件收缩推理规则是等价的。

-有效度提升推理规则和-后件收缩推理规则等价。

首先证明-有效度提升推理规则能够推出-后件收缩推理规则的推理结果。当(→,1)成立且⊆时，有⋂=，应用-有效度提升推理规则有(→⋂,1)=(→,1)。反过来，当(→,1)成立且⊆时，由⋂⊆和-后件收缩推理规则有(→⋂,1)。

与其他推理规则不同，虽然置空推理规则只能推导出不成立的可变决策蕴涵，然而，该推理规则对于受限可变决策蕴涵的完备性是必要的。其原因在于：首先，无论对于决策蕴涵还是可变决策蕴涵（或模糊决策蕴涵），推理过程都是一个动态的过程，是将某条决策蕴涵为真的程度提升的过程。对于决策蕴涵，推理过程是推导出成立的决策蕴涵的过程，也是将该决策蕴涵为真的程度由0 提升为1 的过程；对于可变决策蕴涵，推理过程是将可变决策蕴涵的有效度提升的过程。因此，对于受限可变决策蕴涵来说，类似于决策蕴涵，推理过程是该受限可变决策蕴涵的有效度由0 提升为1 的过程。其次，由受限可变决策蕴涵的语义可知，任意有效度为0 的可变决策蕴涵均可由任意受限可变决策蕴涵集语义推出，因此包含在该受限可变决策蕴涵集导出的封闭集中。因此，为了满足该语义要求，需要使用置空推理规则导出这些受限可变决策蕴涵。换句话说，对于有效度为1 的受限可变决策蕴涵来说，置空推理规则提供了推理的起点；对于有效度为0 的受限可变决策蕴涵来说，置空推理规则提供了推理的终点。

因此，在剥离不确定性后，可变决策蕴涵上只有置空推理规则和-后件收缩推理规则两条推理规则。

定理1 验证了上述分析的正确性。

令={0,1}，L为封闭的受限可变决策蕴涵，则置空推理规则和-后件收缩推理规则相对于受限可变决策蕴涵的语义是完备的，即对L的完备集D⊆L，(→,)∈L当且仅当(→,)可以使用置空推理规则和-后件收缩推理规则从D推出。

充分性。由置空推理规则和-后件收缩推理规则的合理性可知结论成立。

必要性。若(→,0)∈L，则该受限可变决策蕴涵可由置空推理规则得到。若(→,1)∈L，由D是L的完备集可知，D⊢L，因此D⊢(→,1)。此时，由命题3 可知，存在′满足⊆′，(→′,1)∈D，应用-后件收缩推理规则到(→′,1)即可得到(→,1)。

由定理1 可以看出，受限可变决策蕴涵上的推理规则仅仅是决策蕴涵上推理规则的特殊情形。具体来说，-后件收缩推理规则仅仅是扩增推理规则的一个特例；而从推理过程来看，置空推理规则也是决策蕴涵上的推理规则。事实上，如果只关注有效度为1 的可变决策蕴涵，-后件收缩推理规则也可以保证推出所有可以语义导出的有效度为1 的受限可变决策蕴涵。

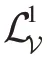
3 受限可变决策蕴涵和决策蕴涵关系研究

可变决策蕴涵是处理有效度为[0,1] 的决策类型，决策蕴涵是处理经典情形{0,1}的决策类型。从处理类型看，似乎可以得出决策蕴涵是可变决策蕴涵的特例，但从语构角度看，受限可变决策蕴涵上的推理规则仅仅是决策蕴涵上扩增推理规则的一个特例。因此，决策蕴涵并不是可变决策蕴涵的特例，相反，受限可变决策蕴涵的推理规则仅仅是决策蕴涵推理规则的特殊情形。下面将从语义的角度论述该结论产生的原因。

下面的定理说明，如果受限可变决策蕴涵集L可以语义导出某些受限可变决策蕴涵，则该受限可变决策蕴涵对应的决策蕴涵也可以被相应的决策蕴涵集L语义导出。

令={0,1}，L为受限可变决策蕴涵集，L为L对应的决策蕴涵集。若L⊢(→,1)，则L⊢→。

由L⊢(→,1)和命题3可知，存在⊆′满足(→′,1)∈L，因此有→′∈L；再由定义3可知L⊢→′。此时，假设╞L，则╞→′，因此当⊆⋂时有′⊆⋂；再由⊆′可知，当⊆⋂时有⊆′⊆⋂，因此╞→，从而L⊢→。

需要注意的是，定理2的逆并不成立，如例3所示。

假设受限可变决策蕴涵集及其相应的决策蕴涵集为：

应用扩增推理规则到→有→⊢→。显然，此时并不存在{⊆′满足(→′,1)∈L，由命题3可知(→,1)并不能由L语义导出。

例3 说明，可以由决策蕴涵集L推导出的决策蕴涵不一定可以由L推导出来；换句话说，在受限的情况下，可变决策蕴涵的推理能力弱于决策蕴涵。该结论事实上验证了语构推理的正确性，即受限可变决策蕴涵的推理规则一方面仅能推导出后件缩小的可变决策蕴涵(如→)，推导不出前件扩大的可变决策蕴涵(如→)；另一方面，受限可变决策蕴涵的推理规则仅能应用于单个可变决策蕴涵，无法像合并推理规则一样应用于两个或两个以上的可变决策蕴涵，因此难以推导出合并推理规则可以推导出的决策知识。例如，在例3中，应用合并推理规则到L可以推导出决策蕴涵→，但该决策蕴涵无法由置空推理规则和-后件收缩推理规则推出。

在语义方面，受限可变决策蕴涵较弱的推理能力会导致难以生成更为紧凑的决策知识集。

令={0,1}，L为受限可变决策蕴涵集，L 为对应的决策蕴涵集。若L是冗余的，则L 必是冗余的。

假设L是冗余的，则存在(→,1)满足L∖(→,1)⊢(→,1)。由命题3 可知，必存在⊂′满足(→′,1)∈L∖(→,1)。显然有→′∈L∖→。由定义3可知L∖→⊢→′。假设╞L∖→，则╞→′，因此当⊆⋂时有′⊆⋂，再由⊂′可知，当⊆⋂时有⊂′⊆⋂，因此╞→，从而L∖→⊢→，L必是冗余的。

定理3 的逆命题并不成立，如例4 所示。

假设受限可变决策蕴涵集：

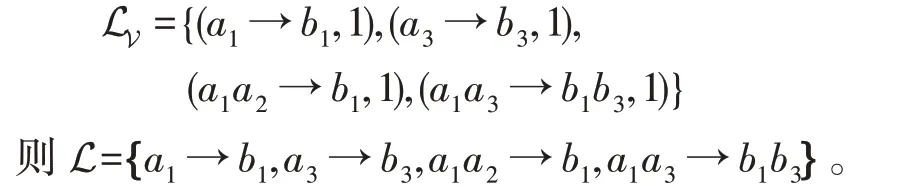
可验证，对任意(→,1)∈L，都有L∖(→,1)⊬(→,1)，因此L是无冗余的。对于L，→可由→应用扩增推理规则推出，→可由→和→应用合并推理规则推出。

定理3 和例4 说明，若L是冗余的，则L必是冗余的；换句话说，若L是无冗余的，则L必是无冗余的。因此，L比L更容易冗余，因而更需要简化，也可以更加紧凑。同样以例4 为例，因为决策蕴涵→和→在L中是冗余的，所以可以简化，即L′={→,→} 可以保持L的所有决策知识，但比L更加精简。相比较而言，在受限可变决策蕴涵框架下，L是无冗余的，因此不可以进一步精简；在决策蕴涵框架下，其中的受限可变决策蕴涵(→,1)和(→,1)事实上是可以精简的。

4 结束语

本文基于已有的决策蕴涵和可变决策蕴涵知识表示框架，分析了受限可变决策蕴涵的语义特征和语构特征，并将不确定性剥离后的可变决策蕴涵与决策蕴涵进行了比较研究。研究结果表明：（1）受限可变决策蕴涵上的推理规则只存在置空推理规则和-后件收缩推理规则两条推理规则，其中置空推理规则并无实际价值，-后件收缩推理规则只是扩增推理规则的一个特例；（2）受限可变决策蕴涵的知识推理能力弱于决策蕴涵；（3）相对于受限可变决策蕴涵，决策蕴涵的知识表示形式更加精简。

虽然受限可变决策蕴涵只是可变决策蕴涵的特例，但无论在语义上还是在语构上都有其独特的特征。主要体现在：（1）语义上，受限可变决策蕴涵不仅允许取值为1，而且允许取值为格中的最大元（如(1,1)），因此受限可变决策蕴涵的语义更为宽泛；（2）语构上，受限可变决策蕴涵上的推理规则为决策蕴涵的特例，但这些推理规则值得进一步研究。一方面，这种研究可以进一步揭示推理规则间的联系，对决策蕴涵来说，有助于发现最优的推理规则；另一方面，受限可变决策蕴涵上的推理规则为决策蕴涵的特例事实上说明这些推理规则更为简洁，因此，基于受限可变决策蕴涵的推理会更为高效。

另外，当前的研究还缺少对决策蕴涵、模糊决策蕴涵和可变决策蕴涵的知识表示和推理能力的比较性研究。接下来将对以上决策类型进行比较性研究。