面向GPU 的直方图统计图像增强并行算法
2022-10-16肖汉孙陆鹏李彩林周清雷
肖汉,孙陆鹏,李彩林,周清雷
1.郑州师范学院 信息科学与技术学院,郑州450044
2.山东理工大学 建筑工程学院,山东 淄博255000
3.郑州大学 计算机与人工智能学院,郑州450001
随着计算机技术的发展,数字图像处理系统应用在安全监控、智能识别和航天遥感等众多领域。由于图像采集容易受到光照以及设备质量等因素的影响,有些图像会存在例如,图像对比度较低、模糊等质量问题。这些质量较差的图像灰度动态范围窄,不能很好展现图像的细节。图像增强技术可以通过对图像信息分布规律的再调整以改善图像质量。传统的直方图均衡方法是一种典型的基于统计学的图像增强技术。该方法数学原理简单,计算方便,理论基础清晰。但是它存在噪声大、细节损失严重等不足,在处理过程中还易出现饱和失真等问题。在充分考虑信息分布与人眼一致性的前提下,各种改进的直方图统计局部增强方法可以对图像信息实现较好的合理分配。图像局部增强可以达到提高图像细节的清晰度,突出图像中需要的信息,改善图像的视觉效果,有利于对图像做进一步的处理。然而,随着图像规模的增加,在不改变算法复杂度的情况下,算法的时间成本将会成倍增长,已无法满足大数据时代下快速处理的需求。
近些年来,CPU虽然有了很大的发展,但还是显示出了其处理性能在功耗墙、存储墙、频率墙和过低的指令级并行等方面的限制。图形处理器(graphics processing units,GPU)在数据并行上具有强大的浮点运算能力和存 储带宽。2020 年5 月NVIDIA发布的基于最新一代GPU 架构“Ampere”的Tesla A100,单精度和双精度浮点计算能力分别可以达到19.5 TFLOPS和9.7 TFLOPS,带宽1 555 GB/s。GPU 作为一种新型的高性能科学计算设备开始进入人们的视野。与CPU 相比,GPU 具有突出的性能优势。
因此,本文将GPU 并行计算和直方图统计算法相结合,着重研究在CPU+GPU 协同计算模型下,局部增强算法如何利用GPU 并行计算资源完成大像幅图像的实时处理,从而验证在该协同计算结构下图像处理算法对于大规模图像的运行效率。该文的主要贡献是通过分析算法的执行特征,根据图像数据的邻接结构,设计了一种基于统一计算设备架构(compute unified device architecture,CUDA)的直方图统计图像增强并行算法,并实现了直方图统计算法在CUDA 计算平台上的naive 版本。基于GPU 的直方图统计并行算法相比单线程CPU 直方图统计算法获得的加速比达到了261.35倍。
1 相关基础与算法分析
1.1 研究现状
王化喆等采用基于直方图统计的局部图像增强算法,取得了较好的图像处理质量。Lei等通过对边缘可靠度的直方图统计,提出了一种快速可靠的二维相位图展开算法,可以达到准实时性能。Yang等提出了一种多属性统计直方图用于图像的自动配准,对噪声和变化的网格分辨率具有鲁棒性。Chu等利用直方图统计方法构造了一个完整的纹理描述符,用于合成孔径雷达图像的分类,在斑点噪声和极低的信噪比方面更具鲁棒性。王勇等通过将亮度控制和直方图分区域均衡进行结合,实现了改进的直方图统计算法,具有良好的视觉效果。Ye等通过在全局方式的对比度差异的约束下进行局部增强,提出了一种用于在线鱼类行为监测的自动图像增强方法,避免了假阳性检测。Zhu等运用连通域的直方图统计量来识别和统计储粮中的昆虫,实现了昆虫识别计数方法。周启双等利用直方图原理,实现了基于标准差改进和局部均值的自适应直方图统计算法,影像局部对比度增强。He等采用texton 聚类和直方图统计等策略,提出了一种新的用于合成孔径雷达图像分类的统计分布纹理特征。吕新正等提出了一种改进的脉冲分选算法,算法采用直方图统计和PRI(pulse repetition interval)变换相结合的方法,采用多DSP(digital signal processor)并行处理的方法提高了运算速度。Yang等提出了一种结合强度梯度和强度统计直方图的标记边缘检测器,提高了道路标记检测的平均召回率和准确率。胡英帅通过将极坐标直方图统计在CUDA 平台上进行并行化,Shape Context算法的速度得到很大提高。Karbowiak通过使用图像直方图实现了图像锐化和更改颜色强度的变换,在GPU 上实现了自动图像标签算法并提高了效率。Gocho等提出了一种基于GPU 的高效SAR 图像变化检测分析器,用于对子图像进行直方图分析以实现SAR 图像的变化检测,获得了57.5 倍加速比。裴浩等提出了基于GPU 的直方图并行算法,算法用于实现三维空间数据距离的计算,获得了18 倍的性能提升。陈坤等利用现场可编程门阵列(field programmable gate array,FPGA)设计了图像直方图统计算法,提高了数据处理能力和处理速度。
目前国内外大多数研究工作集中在将传统的或改进的直方图统计算法应用到各种专业领域中,从而改善了图像增强效果,增强了图像对比度。有部分研究成果利用GPU实现了直方图统计算法,在应用系统中取得了几十倍的性能提高。还有部分学者基于FPGA平台提出了直方图统计并行算法,提高了算法处理速度。总体来看,在提高直方图统计局部增强算法运算效率方面的研究成果很少,速度的提升也不高。
1.2 CUDA 并行计算平台
CUDA 的应用系统是GPU 和CPU 的混合代码系统。在执行CUDA 系统时,主机端执行的二进制代码在调用核函数时需要将设备端代码通过CUDA API传给设备端。GPU 传给CUDA API 的设备端代码不一定是二进制代码CUBIN,也可能是运行于JIT 动态编译器上的汇编形式的PTX(parallel thread execution)代码。最后传到设备上的是适合具体GPU 的二进制代码,其中的信息多于PTX 或者CUBIN,这是因为CUBIN 或者PTX 只包含了线程块一级的信息,而不包括整个网格的信息。目前,在GPU 上可以运行的指令长度仍然有限制,不能超过两百万条PTX指令。GPU 端二进制代码主要包括网格的维度和线程块的维度,每个线程块使用的资源数量,要运行的指令以及常数存储器中的数据。
执行内核的线程可以访问与线程的生存期相同的高性能线程寄存器。每个线程块都有一个共享存储器(对该块的所有线程可见),具有该块的生存期。只要同一块的线程没有冲突访问,共享存储器就与寄存器一样快。所有线程都可以随机访问具有应用程序生命周期的全局存储器,即数据驻留在全局存储器中,用于多次内核启动。通常,全局存储器比访问寄存器或共享存储器慢得多。当相同halfwarp 的线程同时访问全局存储器时,如果被访问的存储器位于相同的全局存储器段中,则可以将访问合并为单个存储器事务。如果不是,则同时访问导致多个顺序存储器传输。
1.3 直方图统计关键技术原理
设为在区间[0,-1]内代表灰度值的一个离散随机变量,并设(r)表示对应于r值的归一化直方图分量。关于图像均值的阶矩定义为:

其中,是的全局均值,即图像中像素点的平均灰度。
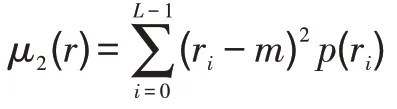
令(,) 表示给定图像中任意像素的坐标,S表示规定大小的以(,)为中心的邻域。该邻域中像素的均值为:

邻域像素的方差为:
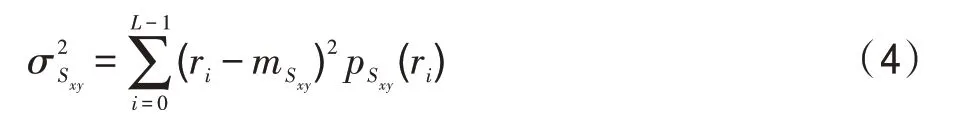

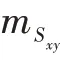
令(,)表示在图像分辨率为×的像素点(,)处的灰度值,(,)表示增强后的图像灰度值。对于=0,1,…,-1和=0,1,…,-1,有:其中,、、是小于1的正常数,是灰度放大系数。
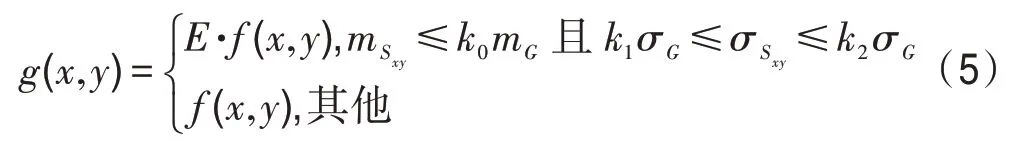
使用模板参与计算,这在图像处理的算法中有大量应用。这些算法有一个相同的运算特征:在对某个像素点进行处理时,需要其模板覆盖范围下的邻域像素点的信息。因此,算法在执行时,需要依据模板大小遍历模板范围内的图像像素。在图像的边界区域运用模板遍历图像时,判断的情况尤为复杂。此时,模板覆盖的图像区域可能已经越过了图像边界。
核函数的逻辑简洁,避免使用逻辑分支控制语句和循环体较短的循环语句,这是并行计算系统性能优化的一个准则。因此,对边界的处理采用传统的判断边界处理法将严重影响系统性能。根据模板的信息,并行算法采用显式扩充边界法来处理图像。图像在完成边界扩充后,模板只需在原图像大小范围内遍历。此时,在扩充图像中不会发生遍历越界问题。核函数的处理逻辑可实现归一化,无需判断边界。直方图统计并行算法采用偶拓展的显式扩边方式进行图像扩充,即第0列被复制到左拓展的第1 列,第1 列被复制到向左拓展的第2 列,以此类推进行四条边界上的拓展。采用边缘像素点附近的点对原图像边界进行扩充,由于像素点邻近,其相似度很高。并且使用图像自身的像素点,既很好地解决了边缘像素点的计算问题,也没有违背图像增强算法的理念。

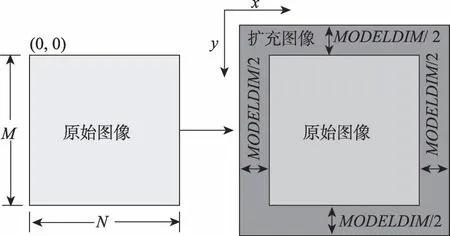
图1 图像拓展示意图Fig.1 Schematic diagram of image expansion
1.4 算法并行分析
对于总灰度级数为的图像进行的直方图统计算法主要包括以下模块:(1)初始化直方图统计图像。该操作需要对整体图像中所有像素点都执行一次,其时间复杂度为(×)。(2)灰度级概率估计计算。要将图像中所有像素点的灰度值分配到某一个灰度级中进行累加,需要执行×次,其时间复杂度为(×)。然后求出每个灰度级的概率估计,其时间复杂度为()。因此,本步骤的时间复杂度为(×+)。(3)图像均值求解。要求计算整体图像的灰度均值和滤波窗口覆盖下的子图像块的灰度均值,其时间复杂度为()。(4)图像方差求解。要求计算整体图像的灰度方差值和滤波窗口覆盖下的子图像块的灰度方差值,其时间复杂度为()。(5)图像扩充。由于需要分别进行原图像左右拓展、上下拓展和保留原图像区域,该步骤的时间复杂度为(×++×/2+×/2)。(6)局部直方图统计计算。需要对×个像素点逐个判断是否进行灰度增强,其时间复杂度为(×)。同时计算某个像素点的局部均值和方差,其时间复杂度为(××(/4+2))。由此可得,直方图统计算法的时间复杂度为(××),步骤(6)是该算法的核心环节。表1 为图像直方图统计算法主要步骤在相同条件下的运算时间。
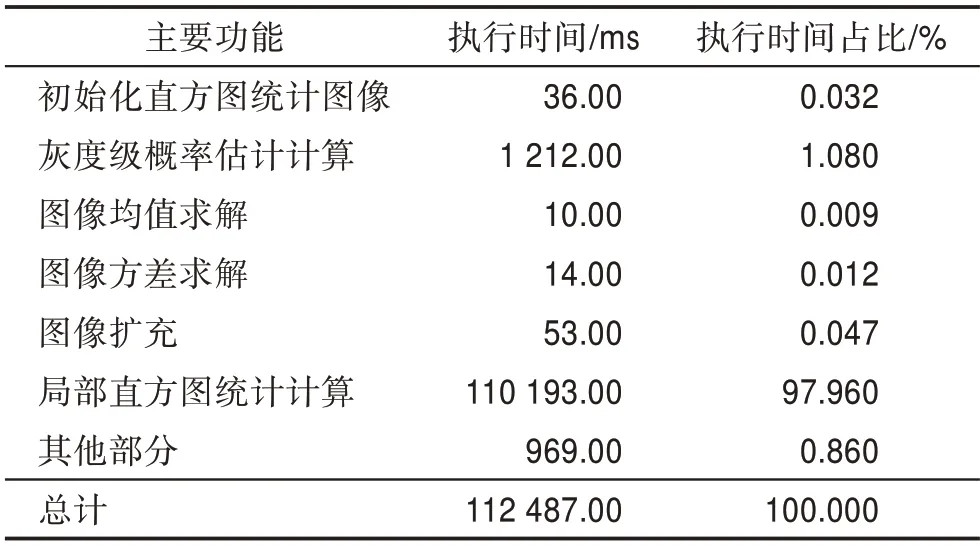
表1 直方图统计算法主要功能运行时间占比Table 1 Proportion of running time of main functions of histogram statistical algorithm
由表1 可见,局部直方图统计计算功能是算法中复杂度最高、最耗时的部分,该模块占用了系统97%以上的资源。显著降低直方图统计算法复杂度的关键是采用高效的快速局部直方图统计方法。因此,对局部直方图统计计算功能结构的优化设计对直方图统计并行算法的实现有着举足轻重的意义。
1.5 直方图统计算法的并行提取
算法的可并行性大小与算法自身存在的任务依赖性有关。任务之间的关联性越低,并行性效果越好,反之则效果越差。通过上面的算法分析,可以得出直方图统计算法具有良好的并行性。具体来说,该算法包含三级并行性:
(1)像素点级并行:为了对图像中包含的隐含特征进行局部增强,需要将图像进行直方图统计,对每一幅图像的每一个像素点的处理是相互独立的,可以并行执行。
(2)均值和方差值级并行:每个像素点的局部均值和局部方差的计算是相互独立的,可以并行执行。
(3)窗口级并行:每个局部统计窗口的处理是相互独立的,可以并行处理。
直方图统计算法的并行性如图2 所示。图2(1)中灰色区域为原始待处理图像区域,进行局部处理时的邻域大小为3×3,白色区域为图像扩充区域。每个方块代表一个像素点。在局部直方图统计计算步骤中,先对像素点进行处理,即求出子图像块1 中的均值和方差,并进行是否增强暗区的判断等一系列操作。然后依次对,,…,,像素点进行处理。子图像块1…子图像块一系列子图像块之间没有相互依赖性,因此,局部直方图统计计算功能可进行并行化处理。
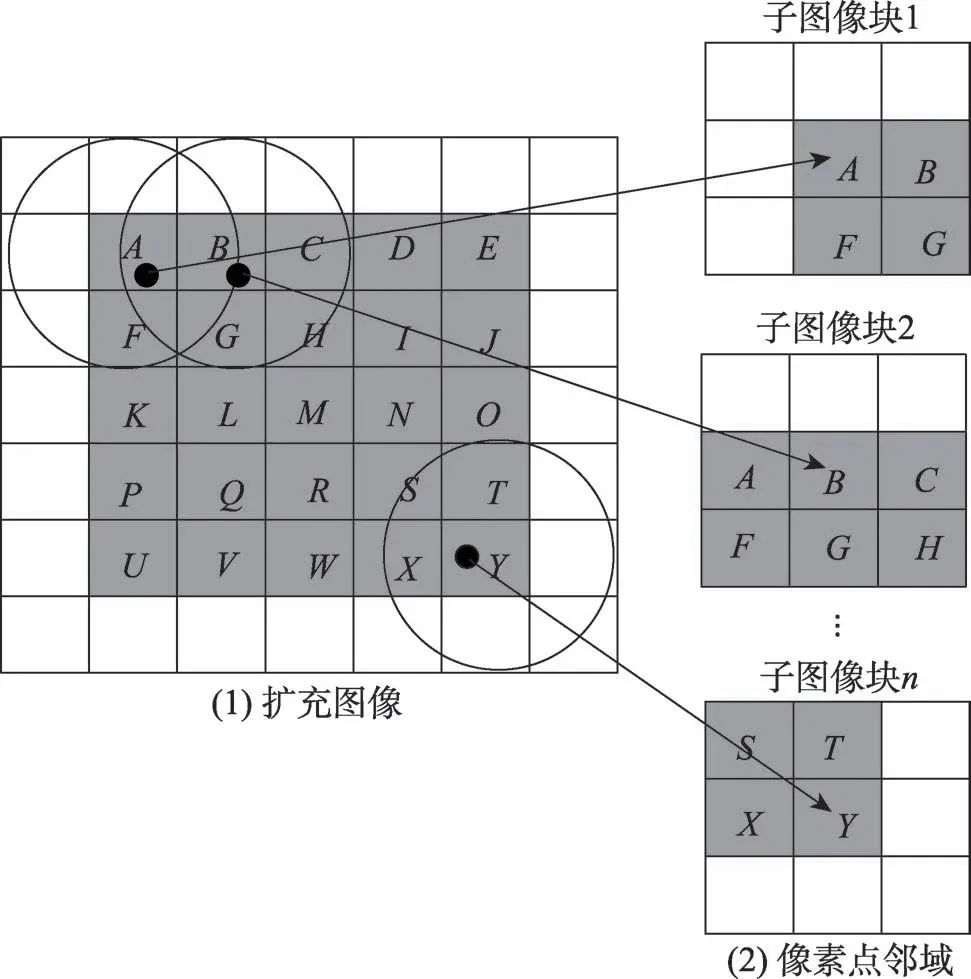
图2 局部直方图统计的并行性示意图Fig.2 Parallelism diagram of local histogram statistics
由此可见,直方图统计算法的计算量非常大并且具备良好的并行性。因此,算法特性非常适合GPU 计算平台大规模并行的架构特点。同时,根据1.1 节对有关研究成果的分析,本文试图采用CUDA平台来解决在异构计算设备上利用直方图统计图像增强算法对海量图像实时处理的问题。实验数据表明,基于GPU 的直方图统计图像增强并行算法在保持算法精度的同时,取得了两个数量级的性能提高。
2 基于GPU 的直方图统计并行映射模型
2.1 并行算法描述
根据CUDA 架构的特点,设在单指令多线程(single instruction multiple thread,SIMT)模型中启动×个线程,每一个线程只负责处理一个像素的局部直方图统计计算,然后把灰度增强值存储到对应的像素点位置。具体直方图统计并行算法形式描述如下。
SIMT 模型上的直方图统计并行算法

假设图像像幅为×,采用GPU 的多线程对局部直方图统计计算部分进行并行计算,一个线程负责处理一个像素点,算法的计算时间复杂度降为()。若在一次内核函数中没有处理完所有像素点,那么每个线程需要执行内核函数至少(×)/次,其中是活动线程的数量。此时,直方图统计图像增强并行算法时间复杂度为((×)/×)。需要注意的是,一般GPU 中可保持的活动线程量很大,即是一个很大的值。因此,存在直方图统计图像增强并行算法时间复杂度((×)/×)≪(××)。
2.2 计算过程
直方图统计并行算法的执行流程如图3 所示。
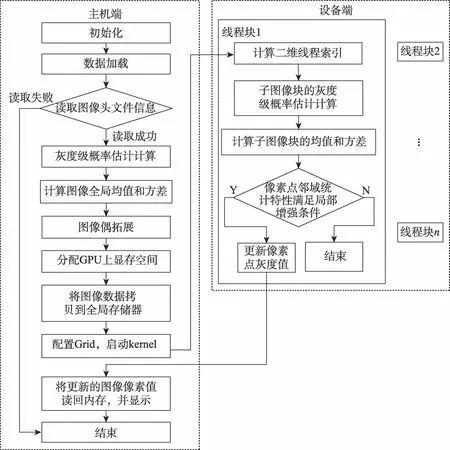
图3 直方图统计并行算法执行模式Fig.3 Execution mode of histogram statistical parallel algorithm
直方图统计并行运算主要实现步骤如下:
(1)获取设备信息和初始化设备。在当前机器上获得支持CUDA 的设备数量,枚举设备信息等,并设置工作设备。
(2)图像预处理。将图像从文件读入主机内存。将文件头结构、信息头和位图信息读入特定的数据结构体中,从而获得图像的高度、宽度和大小等数据。
(3)计算级灰度级的概率密度函数,计算图像整体统计指标全局均值和方差。
(4)图像数据扩展和传输。直方图统计算法在遍历计算到图像边界时,会发生图像数据数组越界寻址的问题,程序中可能会出现空指针异常,从而导致意想不到的错误。因此,采用图像数据扩展方式避免异常发生。
系统将存储在主存中的图像数据传输到GPU 全局存储器中。由于带宽的限制,制约系统整体性能提升的最大瓶颈是主存与显存之间的数据通信。因此,并行算法中采用了整体数据传输,而非多次分块传送。根据图像像幅大小在设备上申请分配存储空间,用于存放由GPU 计算出来的更新灰度值数据。
(5)系统调度内核函数执行直方图统计计算。主要执行下面几个步骤:
①确定内核函数的执行配置。根据图像规模大小,设置网格维度和线程块维度。
②分解图像数据。每个线程块完成所包含的线程需要计算的相关像素点对应点子图像块的有关计算。
③发起kernel,进行线程间的并行计算。每个线程完成与之相应的像素点的有关计算。
(6)更新数据读出并显示图像增强结果。GPU运算结束后,还需将更新后的像素灰度值从GPU 传回CPU。
2.3 算法的加速策略
设计内核函数kernel<<
(1)内核函数参数block 的维度为(T,T),grid 的维度为((+T-1)/T,(+T-1)/T)。、分别是图像的高和宽,每个线程块处理一个子图像块,块内每个线程处理一个像素及其邻域。系统开启线程总数满足((+T-1)/T×(+T-1)/T×T×T)>(×)。
(2)每个线程依据索引地址计算相应像素邻域的灰度级概率密度函数,根据邻域的灰度级概率密度函数计算出像素的局部均值和局部方差。根据像素点邻域的局部统计特性数据判断其是否满足灰度值局部增强条件,并将相应更新的灰度值数据写入主存空间的像素值,如图4 所示。为了实现每个线程对像素点邻域的局部统计特性的计算,在GPU 设备函数中设计了局部均值计算函数和局部方差计算函数。__device__函数是一种设备端的子函数,是由GPU 中一个线程调用的函数。
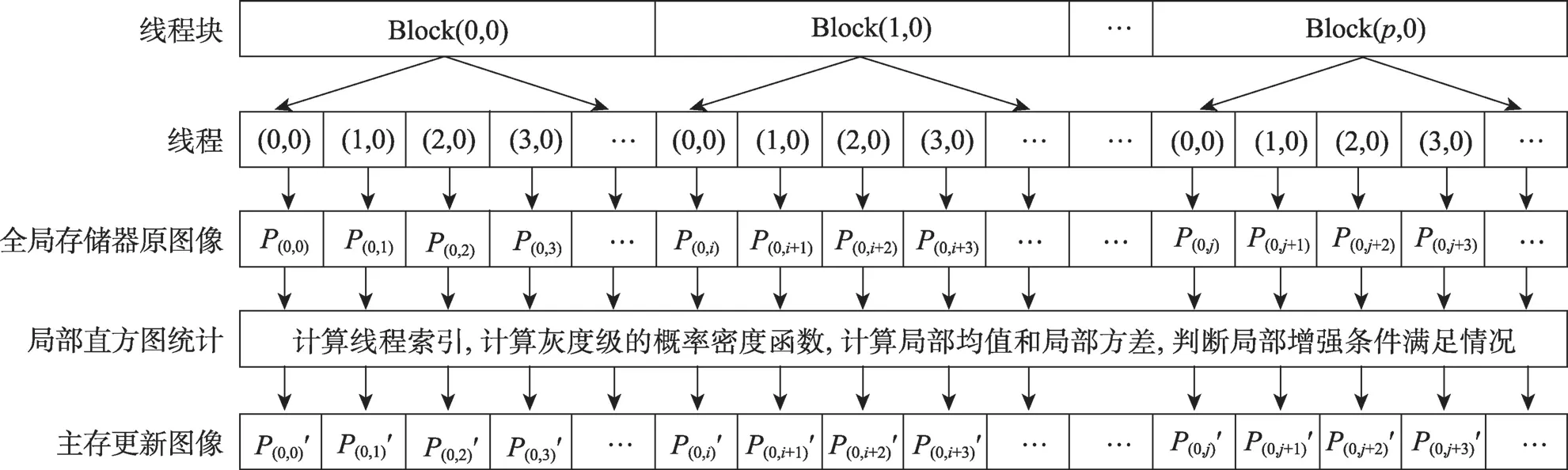
图4 直方图统计划分Fig.4 Histogram statistical segmentation
在CUDA 的执行模型中,需要满足以下三方面的限制:(1)一个流多处理器(streaming multiprocessor,SM)所能并行运行的线程总数的限制;(2)一个SM 所能并行运行的线程块总数的限制;(3)一个线程块所能并行运行的线程总数的限制。一个SM 所能并行运行的线程总数是确定的,为了获得图像直方图统计算法最大的并行计算效率,合理地设计线程块中所包含的线程数目是关键。在对图像直方图统计算法进行GPU 实现的过程中,GPU 中每个SM最多可以激活的线程数目为2 048。由于一个warp一次调度32 个线程,为了提高并行计算效率,一个线程块所包含的线程数应该是32 的倍数。同时考虑线程块中寄存器等资源的限制,设计线程块的尺寸为16×16=256,小于线程块中的最大线程数1 024 的限制。每个SM 运行2 048/256=8 个线程块,小于每个SM 上最多可以激活的线程块数32 的限制。因此,GPU 中的所有线程块和线程都可以同时处于并行计算的状态。
在图像增强中进行局部直方图处理时,由于设置的线程数量大于图像像素的数量,每个线程和处于、平面中的像素成一一对应关系。以式(6)计算得到的线程索引作为相应像素的、维坐标,就可实现线程坐标向像素坐标的转换。即在GPU 上进行图像空间的像素坐标变换计算如式(6)所示。
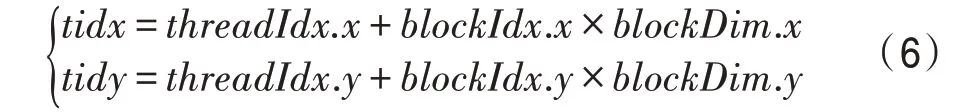
其中,和为某个线程块中的线程分别在和方向的索引,.和.为某个线程块在网格中的和方向的索引,grid在和方向的维度分别为.=(+T-1)/T,.=(+T-1)/T。
2.4 优化设计
在CUDA 上实现直方图统计并行算法的关键是减少数据在主机和设备之间的数据传输。由于主机与设备间的数据传输带宽远低于设备和设备之间的数据传输显存带宽,如果主机和设备之间数据传输次数过多,就会进入传输瓶颈而不能充分发挥GPU的并行运算能力,造成计算效率下降。为了减少数据的传输过程,充分利用GPU 的计算能力,把局部直方图统计计算功能中的全部计算过程全部映射到GPU 上,减少了中间数据在主机和设备之间的换入换出操作,并把图像增强前后的数据一次性在主机和设备之间进行传输。这样就大大减少了传输次数,充分利用了GPU 的计算能力,提高了计算密集度。
在CUDA 计算模型中,系统为了最大限度利用SM 的计算资源,将会定期从一个warp 切换到另一个warp 进行调度线程。由于同一个warp 中的32 个线程是被绑定在一起执行同一指令,应以32 的整数倍设置每个线程块中线程数量,并根据任务的具体情况确认线程块每个维度上的大小。表2 中显示了图像像幅大小为4 357×4 872 时,在线程块中设置不同数量线程时的系统运行时间。从中可以看出,当线程块维度为16×16 时,系统性能最优。

表2 线程块维度对运算速度的影响Table 2 Influence of thread block dimension on computing speed
3 性能评测和分析
3.1 实验条件
硬件平台配置如表3 所示。
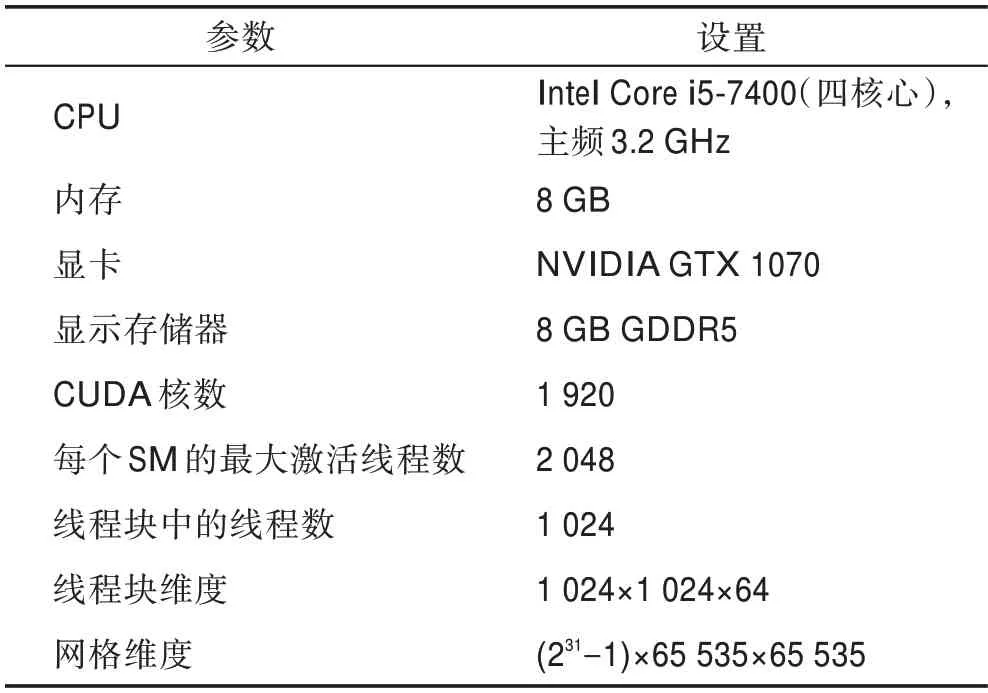
表3 实验环境配置Table 3 Experimental environment configuration
软件平台中操作系统为Microsoft Windows 10 64 bit;MATLAB R2008b;集成开发环境IDE 为Microsoft Visual Studio 2013;多核处理器支持环境OpenMP 3.0;环境支持为CUDA Toolkit 10。
3.2 实验数据与实验描述
串行算法使用的是C 语言实现的图像直方图统计图像增强系统。直方图统计并行算法是采用CPU多核多线程和GPU 众核分别实现的OpenMP 并行系统和CUDA 并行系统。每种算法共执行7 组图像,像幅分别为547×754、1 246×1 652、2 341×2 684、3 241×3 685、4 357×4 872、6 471×6 832 和8 856×8 476。图5分别给出了不同像幅大小的直方图统计算法串行执行与并行执行的图像增强结果。
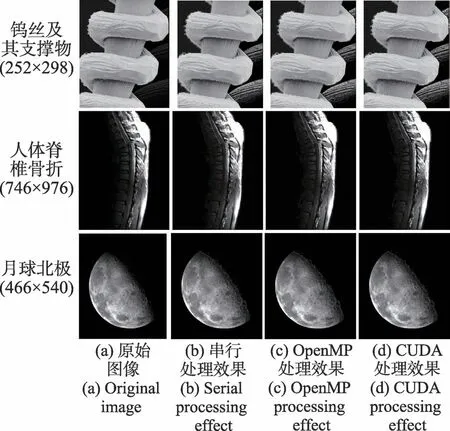
图5 直方图统计图像增强效果Fig.5 Histogram statistics image enhancement effect
表4 给出了直方图统计算法CPU 串行和并行执行时间的统计数据。GPU 并行执行时间分为三部分:初始化、计算和结束。因此,系统总运行时间可以用这三部分时间之和来表示,即=++。其中,是指系统初始化、读取图像数据到内存、为数据分配显存空间和将数据从主存加载到GPU 等的执行时间,是指GPU 计算以及CPUGPU 间数据传输时间,是指把计算得到的结果写回到指定位置的时间。
加速比是指CPU 执行串行算法的总运算时间与并行系统执行并行算法总运算时间的比值。加速比反映了相应并行计算架构下并行算法相比CPU 串行算法整体提升效率情况,可用于对实际系统速度方面的客观评价,如表5 所示。根据表4 和加速比的定义,由表4 中第二列数据与第三列相应数据的比值可得表5 中基于OpenMP 的直方图统计并行算法的加速比。由表4 中第二列数据与第四列相应数据的比值可得表5 中基于CUDA 的直方图统计并行算法的加速比。
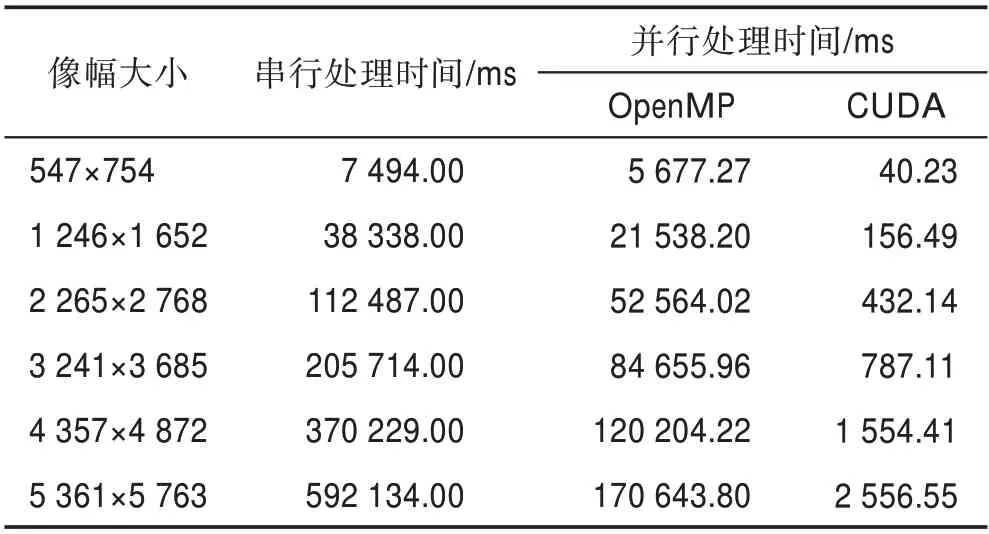
表4 直方图统计算法运行时间对比Table 4 Comparison of running time of histogram statistical algorithm

表5 直方图统计算法性能对比Table 5 Performance comparison of histogram statistical algorithm
3.3 验证并行算法结果
图像直方图统计并行处理的目的是缩短图像处理时间,获得更高局部图像增强速度。然而,如果以损失图像质量为前提,就没有了并行化处理的作用。下面以三组实验图像数据为例进行局部图像增强效果分析。
如图5 可见,原始钨丝图像中部的钨丝和支架都很清楚并且容易分析。图像右侧即暗区域,有部分比较细微的图像几乎看不见。原始图像经过串行/并行直方图统计图像增强处理后,在图像右侧的钨丝,甚至钨丝上的纹路都清晰可见。原始人体脊椎骨折图像左部存在大片的暗淡区域,在经过串行/并行直方图统计图像增强处理后,在图像左部显示出了更多的人骨表面细节。原始月球北极图像右上部存在大片的模糊区域,在经过串行/并行直方图统计图像增强处理后,在图像右上部显示出了更多的月球表面细节。
以上可以看出,原始图像经过串行/并行直方图统计处理后增强了其暗色区域,亮灰度区域被完整地保留,串行/并行处理后的图像展示效果完全一致。
从微观层面上看,将串行系统和并行系统处理三组实验图像数据得到的图像灰度值用直方图表示,如图6 所示。经过分析对比,各组串/并行处理后的图像直方图均相同。
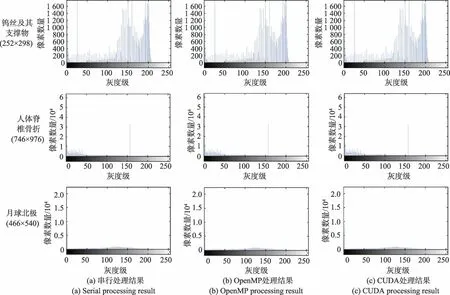
图6 串/并行算法直方图对比Fig.6 Histogram comparison of series/parallel algorithm
由此可以看出,无论是从宏观层面还是微观层面来看,直方图统计串行算法和并行算法虽然在方法设计和运行时间上不同,但是在图像处理的结果上保持一致,从而验证了算法的正确性和可行性。
3.4 讨论实验结果
在直方图统计并行算法的处理过程中,需要原始图像数据的×次存储器读取,直方图统计图像增强数据的×次存储器写入操作。设图像数据大小×=3 241×3 685,每个像素值分配存储空间大小是2 Byte,因此,存储器存取数据总量约为0.048 GB。除以kernel实际执行的时间0.000 22 s,得到的带宽数值是218.18 GB/s,这已经接近GeForce GTX 1070 显示存储器的256 GB/s 带宽了。因此,可以看出,基于CUDA 架构的直方图统计并行算法的效率受限于全局存储器带宽。
从表5 可以看出,GPU 加速的直方图统计算法性能提升明显,但GPU并行算法的加速比随着图像大小的增加呈现缓慢下降的趋势。主要原因是在CUDA并行算法实现中,CPU 负责读取和输出图像数据,而这一过程并没有加速。随着被处理图像大小的增加,读取和输出图像数据所花费的时间也在增加。因此,CUDA 架构下的直方图统计并行算法的性能瓶颈是显存带宽和主存与显存之间数据传输的带宽。
从图7 中可以看出,同样的算法,当计算规模较小时,CUDA 并行计算方式加速效果较为明显,甚至出现260 倍的加速比效果。如图像数据计算规模为3 241×3 685 时,串行算法计算时间为205 714.00 ms,OpenMP 算法计算时间为84 655.96 ms,CUDA 并行算法计算时间为787.11 ms,CUDA 并行方式计算时间远小于传统串行方式和OpenMP 并行方式计算时间。当图像规模较大时,串行算法耗时呈现近直线上升趋势,OpenMP 算法耗时也是一种缓慢上升势头,而CUDA 并行算法耗时只是出现了十分平缓的上升。虽然CUDA 加速效果有所放缓,但仍旧保持了两个数量级的加速。
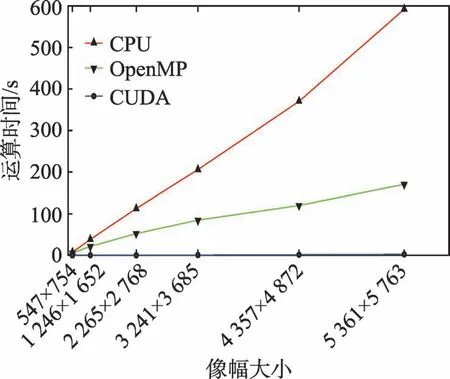
图7 不同架构下直方图统计算法运算时间对比Fig.7 Comparison of running time of histogram statistical algorithm under different architectures
产生该现象的原因是,主机内存和GPU 存储器之间数据交互需要一定的时间开销,图像规模不大时这部分开销对最终的计算时间影响较小,而当图像数据规模很大时,数据交互时间所占比例有所提高,GPU 计算时间不足以抵过传输延迟带来的时间开销,CUDA 加速的效果才出现减缓的趋势。
从图8 可以看出,当图像像幅大小在1 246×1 652以内时,OpenMP 并行方式的加速比曲线斜率变化不大,而CUDA 并行方式的加速比曲线斜率变得较为陡峭;当像幅大小从1 246×1 652 扩展到3 241×3 685时,OpenMP并行方式曲线斜率变化仍不明显,CUDA并行方式的加速比曲线斜率则出现一种缓慢上升的特点;当像幅大小从3 241×3 685 扩展到5 361×5 763时,OpenMP 并行方式曲线斜率仍保持着非常平稳的上升态势,而CUDA 并行方式的加速比曲线则呈现出一种缓慢下降的趋势。因此,从图8中可见,随着像幅规模的增加,CUDA 曲线斜率的变化都大于OpenMP方式曲线斜率变化。
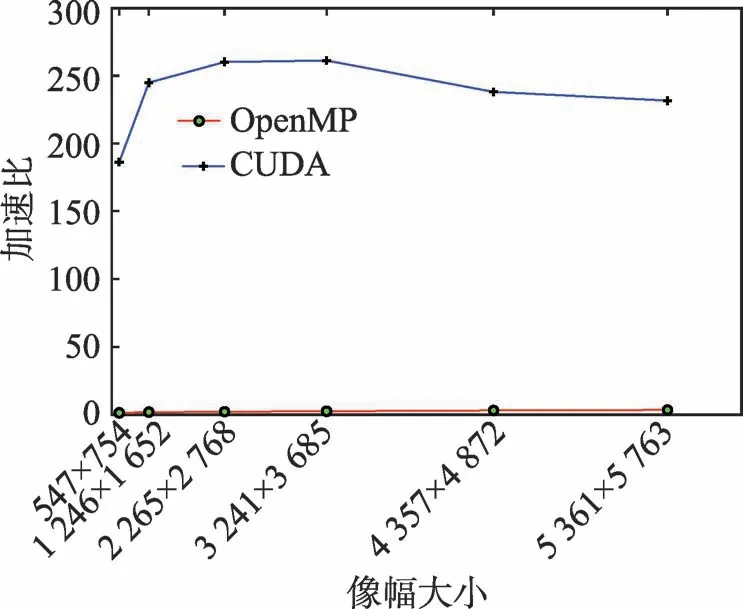
图8 直方图统计并行算法加速比趋势Fig.8 Speedup trend of histogram statistical parallel algorithm
曲线斜率的大小,在一定程度上可反映出数据计算规模与计算时间的关系,即在相同的计算规模下,曲线斜率越大,说明该并行计算方式的时间消耗变化越剧烈。当曲线正斜率较大时,数据计算规模稍微扩大,仅能够导致计算时间的平稳增加,这时计算规模与消耗时间的性价比极高,形成了计算效率的高峰期,但扩展性较差。
根据上述分析,可以看出CUDA 并行计算方式的扩展性不如OpenMP 方式,CUDA 方式更容易形成计算瓶颈。但是,由于CUDA 并行计算方式带来的巨大的加速比优势,在图像像幅大小不断扩大的趋势下,仍然具有OpenMP 传统并行计算方式无法企及的加速效果,因此,CUDA 并行计算方式仍更有优势。
由图8 还可以看出,使用在CUDA 架构上进行GPU 计算,速度远高于基于OpenMP 传统模式的CPU 计算,且随着图像像幅的不断增大,这个速度差距始终保持。这是由于CPU 核心数的限制,CPU 处于满载状态时,很难有较大的性能提升,同时还存在线程创建和调度的额外开销。而在一定的计算量范围之内,GPU 中每个线程的计算时间大致相同,计算时间的增加仅仅由于更多的线程和线程块与硬件之间交互造成的必要时间开销。
4 结束语
本文提出了一种基于CPU+GPU 协同计算的直方图统计的图像增强并行算法。首先进行核函数基本配置设计和任务划分映射,使该并行算法在GPU上可执行。然后通过优化数据传输和优化线程块资源配置,进一步将并行算法的执行效率提高。实验结果表明,在NVIDIA GTX 1070和Intel Core i5-7400 CPU组成的实验平台上,使用并行算法进行了三组直方图统计图像增强实验,相比单线程CPU 算法最大加速比达到了261.35 倍,可以满足大数据图像的实时处理需求。此外,将经过本文方法与传统CPU 串行算法处理后的图像采用直方图计算比较,二者在宏观和微观层面结果均保持一致,验证了方法的正确性。文中采用的并行优化方法,对其他图像处理算法在GPU 计算架构下的实现和优化也具有很好的指导意义和参考价值。
本文所完成的工作还有进一步优化的空间,还有待做更深入的研究:数字图像本质上就是一个二维数组,每个像素的处理过程是相互独立并且完全一样的计算过程。因此,可以在GPU 集群上采用MPI 和CUDA 相结合的技术,由MPI 完成更大图像块之间的并行,由每个节点上的GPU 完成图像块内的并行,通过GPU 集群可以使处理速度更快,争取在更短的时间内完成更大尺寸的图像处理工作。
