重载列车机械传动系统轴承振动信号分析与故障研究

■ 文/袁 媛

机械传动系统轴承在重载列车安全运行中发挥着极为重要的作用，相关研究表明，重载列车机械传动系统故障30%以上是由轴承引起，加强传动系统轴承状态监测及故障识别、诊断成为该领域管理人员关注的问题。随着科技的进步与发展，我国在机械传动系统信号处理方面取得了一定的进展，但基于振动信号的复杂性，尚不能完全对振动信号特征做出正确的分析，基于此，研究引入EEMD 算法与BP 神经网络算法，对其振动信号分析及故障诊断问题进行探讨，以期为相关领域提供借鉴。

1 重载列车机械传动系统轴承的特征

1.1 机械传动系统轴承结构

机械传动系统轴承结构如图1所示，主要部件包括内环、外环及传动体等，外环与轴承座紧密结合在一起，一般不会出现振动位移；内环与机械、设备传动装置等相连接，跟随传动装置转动。传动体为轴承的核心部件，通过将滑动摩擦转变为滚动摩擦，降低机械设备损耗率与故障率。目前，重载列车常用轴承主要为球形与圆柱形，在内外环均有凹槽滚道设计，能够对轴承轴向移动起到限制作用，减少接触应力。

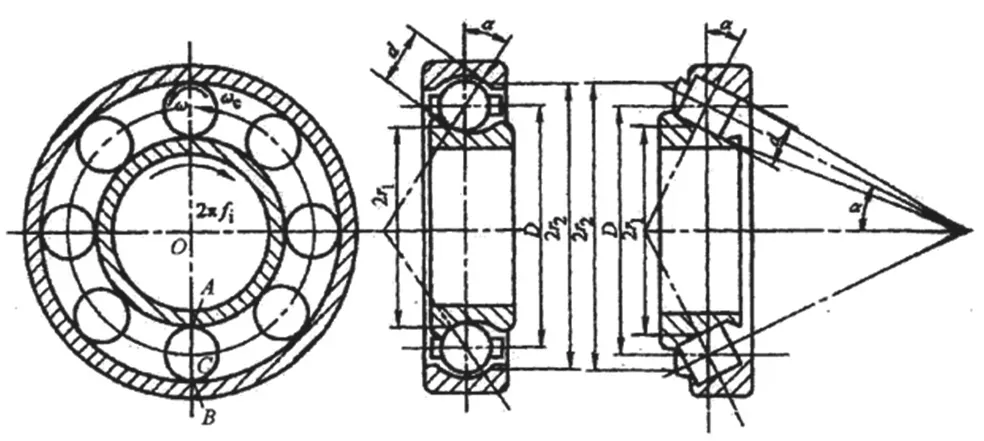
图1 滚动轴承基本结构图

1.2 机械传动系统轴承故障常见形式

机械传动轴承故障与安装、载荷、异物侵入等多种因素有关，且随着长时间的运转，轴承关键部位会出现不同程度疲劳、磨损，导致无法进行正常工作。常见的轴承故障包括以下几种：①磨损。当轴承处于正常运转状态下，其内外环伴随滑动状态，接触面上容易受到磨损。另外，氧化物、金属粉末等侵入会破坏轴承封闭性，造成磨损。轴承零件的接触面磨损常与润滑不良有关。磨损直接影响着轴承使用寿命，进而影响重载列车运行安全性。②疲劳。轴承内外环在运转过程中不仅要承受载荷，而且存在相对滚动状态，容易在接触面形成裂纹，进而引起剥落，这一现象的根本原因为疲劳。研究报道，当滚道疲劳剥落坑大于0.5mm2提示轴承寿命终结。③压痕。轴承在过载或偏载情况下运转，或受到冲击、密封损坏，会导致轴承内外环或滚道面出现压痕，引起轴承故障。④腐蚀。与润滑油脂、轴电流与轴结合程度密切相关，当含有水分或酸类的润滑油与轴承表面金属发生反应会产生化学腐蚀。电流击穿油膜，在内外环滚道出现凹坑为电蚀。

1.3 机械传动系统轴承振动信号特征

重载列车机械轴承结构简单，但运转过程较为复杂，其振动信号特征可以从如下3 个方面进行分析：①磨损引起的振动。轴承出现磨损后，轴会以轴承外环为中心进行振摆，振动频率显著高于滚动体的公转频率，若转动一周触发的振动数增大，提示轴承存在严重故障。且振动信号峰值、方根会随着磨损程度的加剧而升高。②点蚀引起的振动。轴承的压痕、剥落等损伤会引起振动，点蚀部位及冲击位置不同，振动振幅也呈现出一定的差异性。③烧伤引起的振动。润滑不良是轴承烧伤的主要因素，导致轴承运转受到影响，由于烧伤与粘合时间短，定期检查不易发现，且烧伤越严重，振动幅值增大越明显。

2 重载列车机械传动系统轴承振动信号分析及故障提取

2.1 时域诊断方法

时域特征变化趋势能够对常规轴承故障诊断提供指导，在振幅值诊断时，Xp 表示峰值，经过绝对值处理后，将其有效值记为Xrms，其能够对某时刻振幅最大值予以反映，适用于瞬时冲击的故障诊断，有效值则更适合磨损类故障诊断。波峰因数（Xp/Xrms），通常不容易受到轴承尺寸、转速及载荷的影响，对于点蚀类诊断有着较高的指导意义。伴随时间的变化，Xp/Xrms 可对轴承故障进行早期诊断，呈现故障发展趋势。当故障扩展到一定程度，峰值会达到极限值。在进行峭度系数诊断时，峭度K 为归一化四阶中心距，主要用于量度振动幅度概率密度函数，计算公式为：

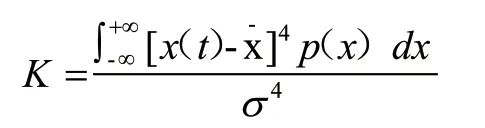
2.2 基于EEMD 的轴承频域故障特征提取

轴承故障类型不同，固有频率也呈现一定的差异性，随着频率分布的变化故障振动信号也会随之改变。此次研究在轴承故障振动信号提取中引入能量熵概念，首先采用EEMD法分解轴承振动信号，能够获得IMF 共k 个，然后计算出对应的能量，即E1，E2，…，Ek。基于EEMD 分解的正交性，排除残余项的影响，原始振动信号总能量即k 个IMF 能量的和。IMF 分量频率具有一定的差异性，能量不同，轴承振动信号能量分布对应的EEMD 能量熵可以用如下公式表示：

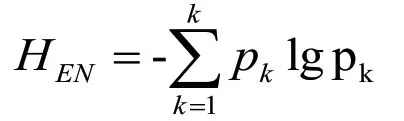
其中：pk表示第k 个模态函数能量在总能量中的占比。根据上述方法对内外环故障轴承加速度信号能量熵进行计算，设置采样率为12000sample/s，转速以1730r/min，计算了5 组不同状态轴承的EEMD 能量熵，结果如表1所示。

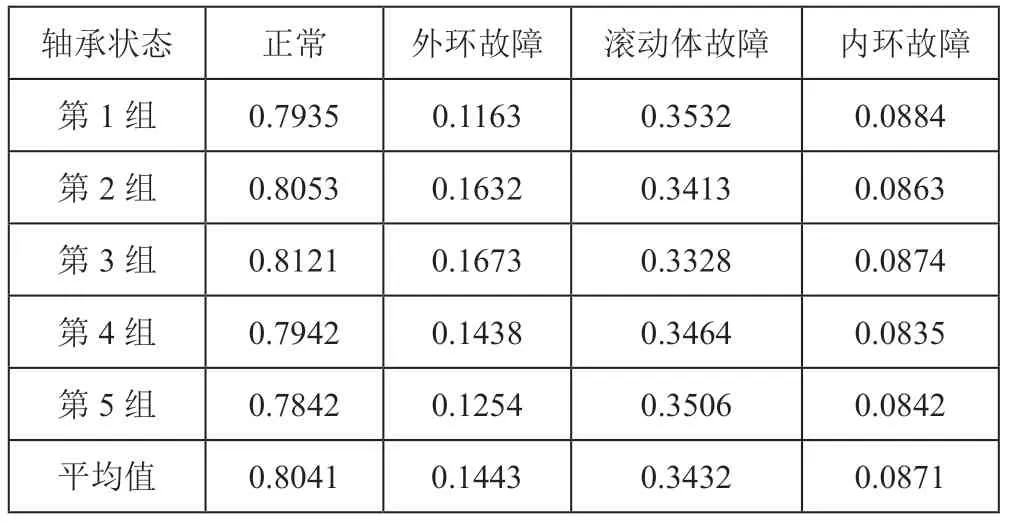
表1 5组不同轴承状态的EEMD能量熵

由上表可知，与轴承故障状态相比，正常轴承能量熵值明显较高。当处于正常运行状态下，振动信号平均，且具有一定的不确定性。而在内外环故障状态下，固有振动频带会产生共振频率，此时频率带集中了振动冲击能量，降低了不确定性，且伴随能量熵值的降低。考虑是由于外环故障、滚动体故障更为严重且比较集中。通过对EEMD 能量熵值变化的分析能够掌握轴承运行状态，便于故障类型的判断。因此可以利用EEMD 获得IMF 能量，将其作为特征向量对轴承工作状态予以判断，进而获得准确的故障识别。

通过EEMD 分解获得IMF，表示不同时间特征下的平稳信号，轴承故障情况均可以通过不同尺度对应的能量变化反映。基于此研究需要引入BP 神经网络，对轴承工作状态及故障予以判断。EEMD 的IMF 能量特征提取步骤：为EEMD分解原始振动信号并进行优化处理；为第k 个IMF 分量（Ek）表示为：

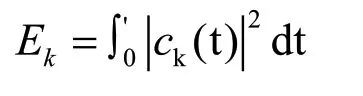
将能量作为向量元素，其特征向量为：

T=[E1，E2，E3，E4，E5，E6，E7，E8]

那么，

T'=[E1/E,E2/，E3/E，E4/E，E5/E，E6/E，E7/E，E8/E]

3 基于BP 神经网络的重载列车机械传动系统轴承故障诊断

BP 神经网络主要优势为工作状态稳定、结构简单，将EMD 分解获得的IMF 能量特征向量直接输出，能够输出期望值，对轴承故障状态及诊断结果予以映射，且无需构建模型，具有较高的精度，诊断轴承故障系统结构如图2所示。

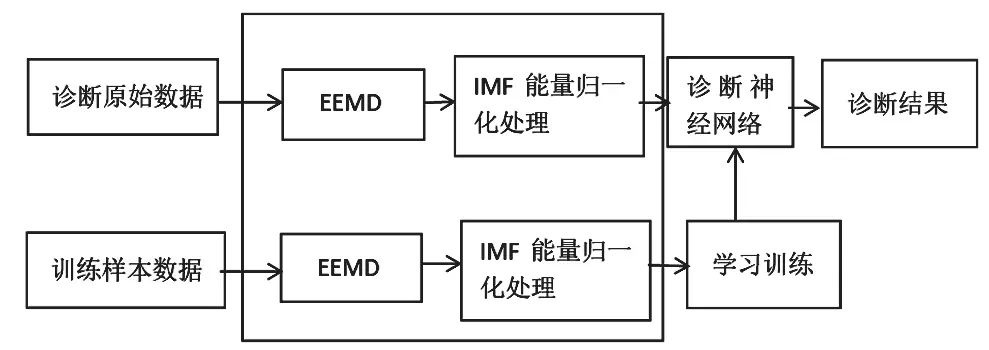
图2 BP神经网络轴承故障智能诊断系统

3.1 隐层数与节点确定

在隐层数设计方面，采用单隐层感知器能够对连续函数予以映射，若隐层节点数多仍无法提升网络性能，需要加入第二个隐层。在实际问题中，可以应用双隐层隐节点以减少隐节点数，若仍然无法降低训练误差，可增加多层感知器设计。在隐节点数设计方面，能够提取样本中内在规律，对应若干权值，且每个权值均能够强化网络映射能力。神经网络与隐节点数量具有一定的相关性，隐节点数量越少，获取信息能力会降低，难以反映样本规律；过多的隐节点数量会对非规律性内容进行干扰，导致BP 神经网络辨识能力下降。本研究采用试凑法以明确最佳隐节点数量。首先设置少隐节点训练网络，根据实际情况适当增加，明确误差最小的隐节点数，其公式为其中nh表示的是隐层节点数，输入与输出层节点数分别用ni、no表示，a 表示1～10 常数。

3.2 传递函数与训练算法

在隐含层采用S 型激活函数，线性激活函数适用于输出层，在BP 神经网络计算中引入双曲正切S 型激活函数，为提升收敛速度，减少计算量与内存量，可以应用弹性BP 法实施网络训练，且能够帮助轴承故障诊断。

3.3 输入、输出层节点数与样本选择

将轴承工作状态类别作为输出层节点数，每个输出节点均与一种工作状态对应，本研究将轴承工作状态分为外环、内环故障、滚动体故障和正常4 种状态，设计4 个输出层节点，对实际样本输出情况进行识别与检验，并考察节点输出情况，对对应的工作状态及故障类型予以判断。若最大与最小节点数值差异小，无法对故障进行分辨，将会拒绝识别。

3.4 基于BP 神经网络训练与测试结果分析

研究选择32 个测试样本，每种状态设计8 个样本，根据初始隐层节点数计算公式，获得初始节点数为5，将训练后网络输出均方误差控制在0.0001，可以发现，隐层节点数增加后，迭代次数会减少。如表2所示，当隐层节点＞7，经过迭代处理，仿真测试了经过训练的样本，可以发现网络结构8-9-4时，减少了BP神经网络迭代次数，但具有较高的精确度，训练样本准确率为93.3%，识别率为87.5%。该算法能够对轴承工作状态予以准确判断，切实可行。

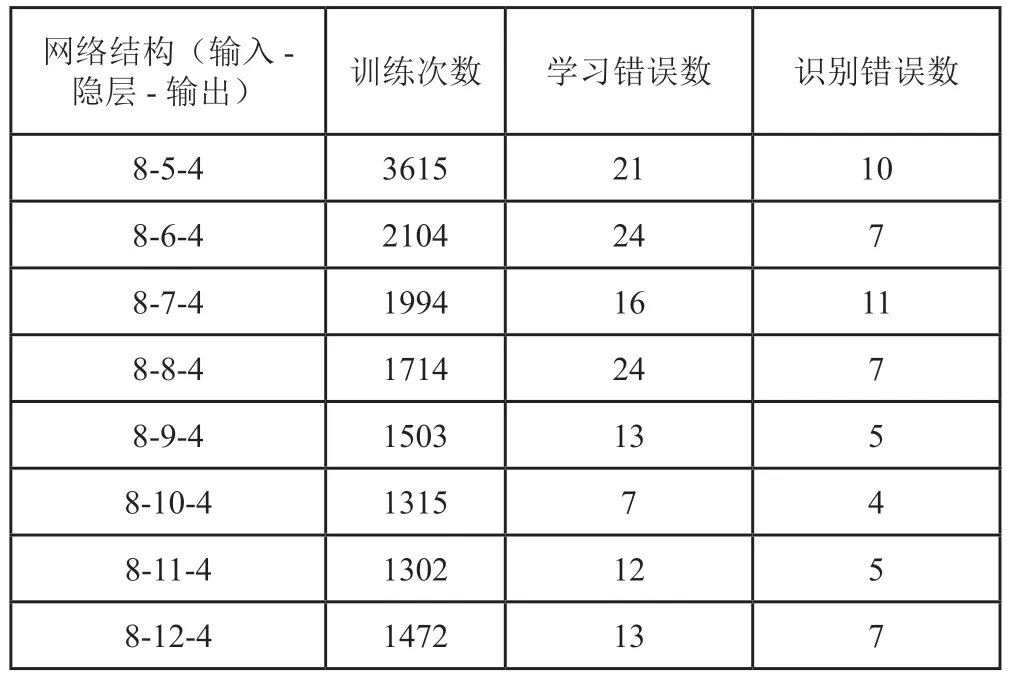
表2 基于BP神经网络训练与测试结果分析

4 结语

综上所述，应用EEMD 模函数能量作为特征输入到BP神经网络系统，实际输出值与期望值接近，识别性能高，能够对轴承工作状态予以准确识别，掌握其故障类型，具有较高的可行性。