考虑感染因子的公共场所人员调度优化研究——以图书馆为例

王芳，白云，龙建宇，曾波

（1.重庆工商大学 管理科学与工程学院，重庆 400067；2.东莞理工学院 机械工程学院，广东 东莞 523808）

0 引 言

2019年新冠肺炎病毒被发现以来，迅速席卷各地并延续至今，给我国社会生活、经济发展和人民群众的生命和财产安全造成了巨大的影响和干扰，被世界卫生组织列为国际关注的突发公共卫生事件，严重威胁社会公众的日常生活工作。经过艰苦抗疫，我国进行入了疫情防控常态化阶段，疫情防控与经济复苏同步推进。但是自2022年3月以来，全国各地再次爆发了不同程度的疫情，多个高校和地区深受其影响，必须实行“非必要”不出门、公共场所暂不开放等防疫政策。

公共服务是现代政府的基本职能，服务型政府建设是我国行政管理体制改革的重要目标之一，公共服务体系是政府部门为居民提供公共产品与公共服务的一整套体系。在新冠肺炎疫情应对中，人民群众的生产生活需求发生重大变化，公共服务的供给必须既要保障基本民生需求也要考虑疫情控制需要。随着进入后疫情时代，为满足人民群众的各项需求，公共场所逐渐对外开放，开始正常运营。公共场所是面向社会大众开放的，人员密集、流动量较大等使得公共场所成为疫情防控工作体系重要的环节之一。由于新冠病毒传播存在复杂性和不确定性，在新形态危机下保障人民群众的生命安全，公共场所管理尤其是公共场所的人员调度问题面临着前所未有的挑战。

以高校图书馆为例，因其服务功能和定位，使得其具有人群密集程度高、流动性大、场馆相对封闭、书籍资料等全面消毒难度大等特点，所以图书馆极易成为疫情感染的场所。在疫情发生前，其可面向全社会各个阶层读者免费开放，具有社会性，与社会发展现状紧密联系；在疫情发生后其是面向全校师生免费开放，提供查询、借阅及相关服务，开展社会教育的公共文化设施。因此，后疫情时期需要图书馆在新形态危机下积极应对，保障学生、馆员等人员的生命安全，故提出在考虑新冠病毒感染风险的条件下，针对图书馆员工排班、学生进馆流量控制等工作，需要不断完善图书馆的管理制度的要求。

近年来，由于运筹优化算法的发展和计算机技术的应用，关于任务指派和人员调度问题的研究得到了进一步的拓展。现有的关于公共场所的员工调度的研究主要集中在交通、制造业、呼叫中心、医疗卫生等系统中，李建斌将“巡检路线排班最佳”转化为TSP 动态规划问题，用贪婪算法分析每班每人近似最佳路线，考虑错时交班得出遍历图，应用Mathematica 编辑对路线进行模拟分析。在新冠肺炎疫情蔓延期间，考虑到病毒传播的因素，国内外对人员调度优化的研究主要集中在医疗系统中。Mehmet等人研究了新冠肺炎流行期间土耳其一家医院医生轮班表的准备工作，提出了一个混合整数规划模型并将其转化为一个决策支持系统，在减少病毒传染的风险下，维持了所有部门的医疗保健服务。Kosasih Bai Asmita等人在疫情爆发期间对雅加达一家公立医院的急诊室护士调度进行了研究，在保证急诊室护士和患者的比例保持在1：4 的最低比例的前提下，通过改进的Tribrewala、Phillipe 和Browne（TPB）算法对轮班模式进行了优化。刘亚兰等人研究了新型冠状病毒性肺炎疫情期间基于多目标整数规划模型的护理人员排班，在满足不同班型人数需求及患者救治所需的前提下，以最大限度减少护理人力资源和防护用品的消耗为目标，确立目标函数、约束条件及相应的参数，通过MATLAB 软件建立多目标整数规划模型并运用CPLEX 求解器求解。Giorgio Zucchi等人研究了在新冠肺炎疫情蔓延背景下，意大利一家大型药品配送仓库人员调度问题，他为降低病毒感染的风险将员工分成相互排斥的组进行工作。Selman Aslan等人通过使用多目标遗传算法和资源受限的项目调度技术，使用COVID-19 感染率建模来解决建设项目案例的项目工期、大流行风险和项目成本。

传统的研究方法可以解决员工的排班问题，但是目前新冠病毒的传播仍具有复杂性和不可确定性，以上对新冠肺炎期间的人员调度研究大多集中在医疗系统，其他系统的员工排班研究也必须提上日程。所以在疫情常态化阶段，人员调度问题的研究需要结合防控要求，尽量减少人员的流动性，从而减少感染风险。结合以上研究，本文根据研究问题的特征结合后疫情防疫要求建立了混合整数线性规划模型，用于解决后疫情时期公共场所的人员调度问题，将员工分成互相排斥的小组，通过感染因子来衡量排班后员工感染病毒的风险，使用数学规划求解器GUROBI 在短时间内获得问题的最优解，不仅可以对提高员工满意度和服务对象满意度，而且对图书馆的运营效率和成本也有着显著影响。

1 问题模型构建

1.1 模型假设

模型的假设条件为：（1）所有的员工，对各部门的工作内容与业务流程都熟悉，即任意员工都可胜任任意部门的工作；（2）默认周天为所有员工的休息日，图书馆闭馆不进行开放。

1.2 模型参数及变量定义

1.2.1 参数与集合

计划周的排班方案，一周24 个班次，则作出以下定义：

：班次的集合，其中∈｛1，2，…，24}；

：员工的集合，其中∈｛1，2，…，}；

：部门的集合，其中∈｛1，2，3}；

e：第∈班次的开始时间；

l：第∈班次的结束时间；

d：第∈班次中需要办理业务的学生人数；

P：员工∈办理业务的效率（单位小时内能够服务的学生人数）；

C：单位最大最小工时差成本；

C：平均人力成本。

1.2.2 决策变量

：所有员工中最大的总工作时数；

：所有员工中最小的总工作时数；

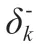
x：员工∈若在部门∈的班次∈中工作，则x=1，否则为0；

y：员工∈若在部门∈中工作，则y=1，否则为0。

1.3 模型目标函数及约束条件

考虑到公共场所人员调度问题是一个复杂的问题，由于服务质量、人力成本和学生满意度是影响排班的主要因素，而且服务质量和人力成本存在二律背反的关系，所以在建立模型时，将总成本分为排班出现怠工现象导致的人力成本和不能达到服务水平要求的惩罚成本，以总成本最小为目标，以各班次中学生到馆办理业务的数量等作为输入参数，以员工在某一部门的某一班次中工作等作为决策变量，建立排班优化模型，目标函数为：

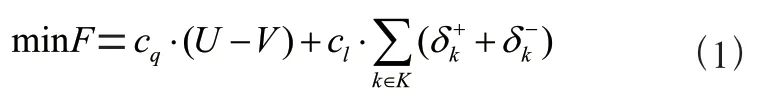
周一至周六为工作日，三个部门的各班次必须有员工上班，故需满足以下约束条件：

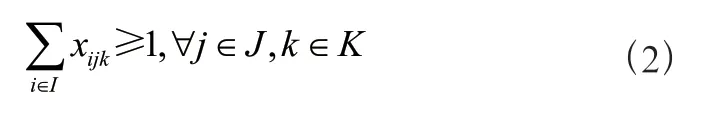
在没有疫情时，图书馆排班制度允许员工串部门轮班，但在后疫情时期，为配合疫情防控工作从而降低病毒感染的风险，要求员工始终在某一部门工作，不进行串部门轮班，故需满足：

为提升员工的工作积极性与工作效率，要求员工不允许连上两个班次，且上晚班的员工次日不再安排早班，保证员工有充足的休息时间，故需满足：

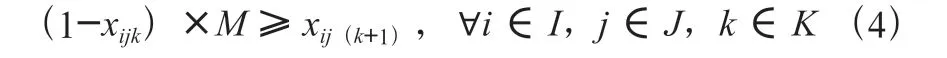
决策变量x与决策变量y的耦合关系应满足以下关系：

x≤y∀，∈，∈

为平衡员工之间的工作时长，提升员工的满意度，故要求所有员工∈在部门中的最大总工作时数U 与最小总工作时数V 之间的差越小越好，即员工之间的工作量达到均衡，故员工中的最大总工作时数U 与最小总工作时数V可表示为：

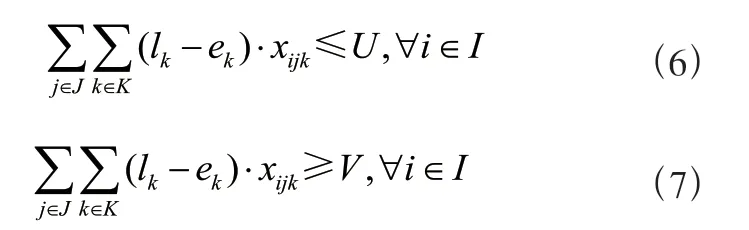
不仅如此，还要尽量满足学生办理业务的需求，即员工排班既要避免出现怠工的现象，又要在规定的上班时间内避免因工作效率低下而未达到学生期望的服务水平。

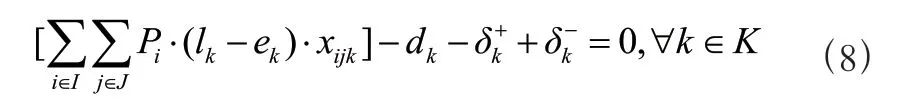
2 实验设置

2.1 案例数据收集与处理

本文所有测试是在3.40 GHz CPU 计算机上进行，使用Python 和9.1.2 版本的GUROBI 优化软件，平均求解时间为15.062 s。以图书馆信息服务部为例，利用实际数据对模型进行验证。

2.1.1 部门数

图书馆信息服务部分为3 个部门，包括信息服务中心，负责办理相关一卡通业务，如一卡通挂失、补卡等；服务管理台1，负责检查监督学生入馆、前台咨询和逾期图书缴费等其他图书馆前台管理工作；服务管理台2 归还图书的分类和归放等工作，故=1,2,3。

2.1.2 员工数及效率

三个部门总共需要8 个员工，故={1,2,…,8}，每个员工办理业务的效率如表1所示，其中办理业务的效率为单位小时内办理的业务数量。

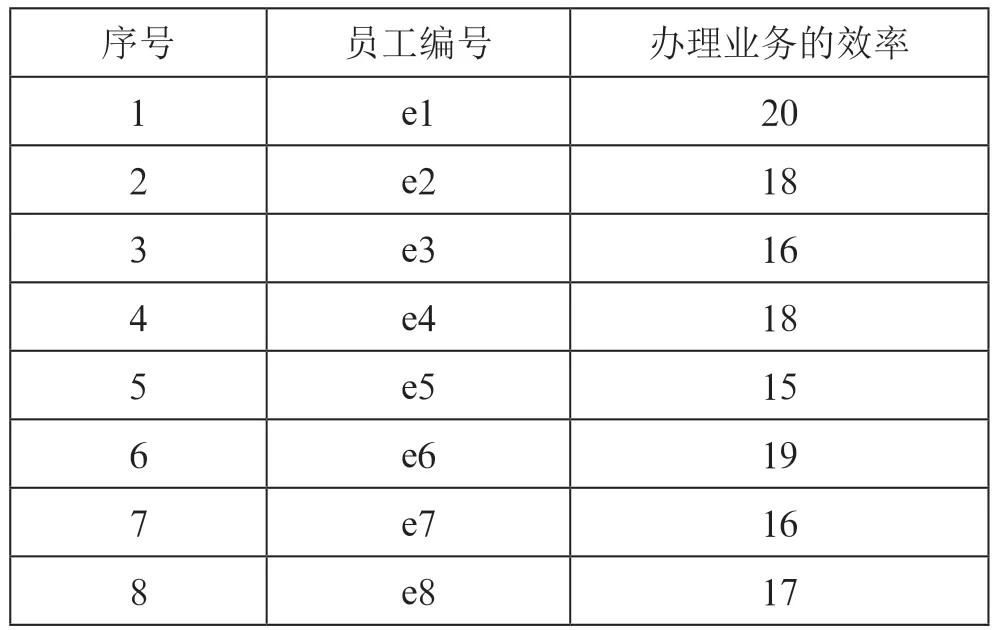
表1 员工编号及效率

2.1.3 班次

通过对办理业务的学生数量进行过统计和分析，发现原有的轮班制度不仅存在未将疫情防控要求考虑在内的缺陷，而且排班方案也不合理。故对班次做出调整，一天分为早班、中班、下午班以及晚班4 个班次，一周共有24 个班次，具体的上班时间如表2所示。

表2 上班时间表

2.1.4 办理业务学生数

对原始数据处理后，本文测试的各班次办理业务学生数是从实际统计数据中随机生成的。一周24 个班次办理业务的学生数如表3所示。

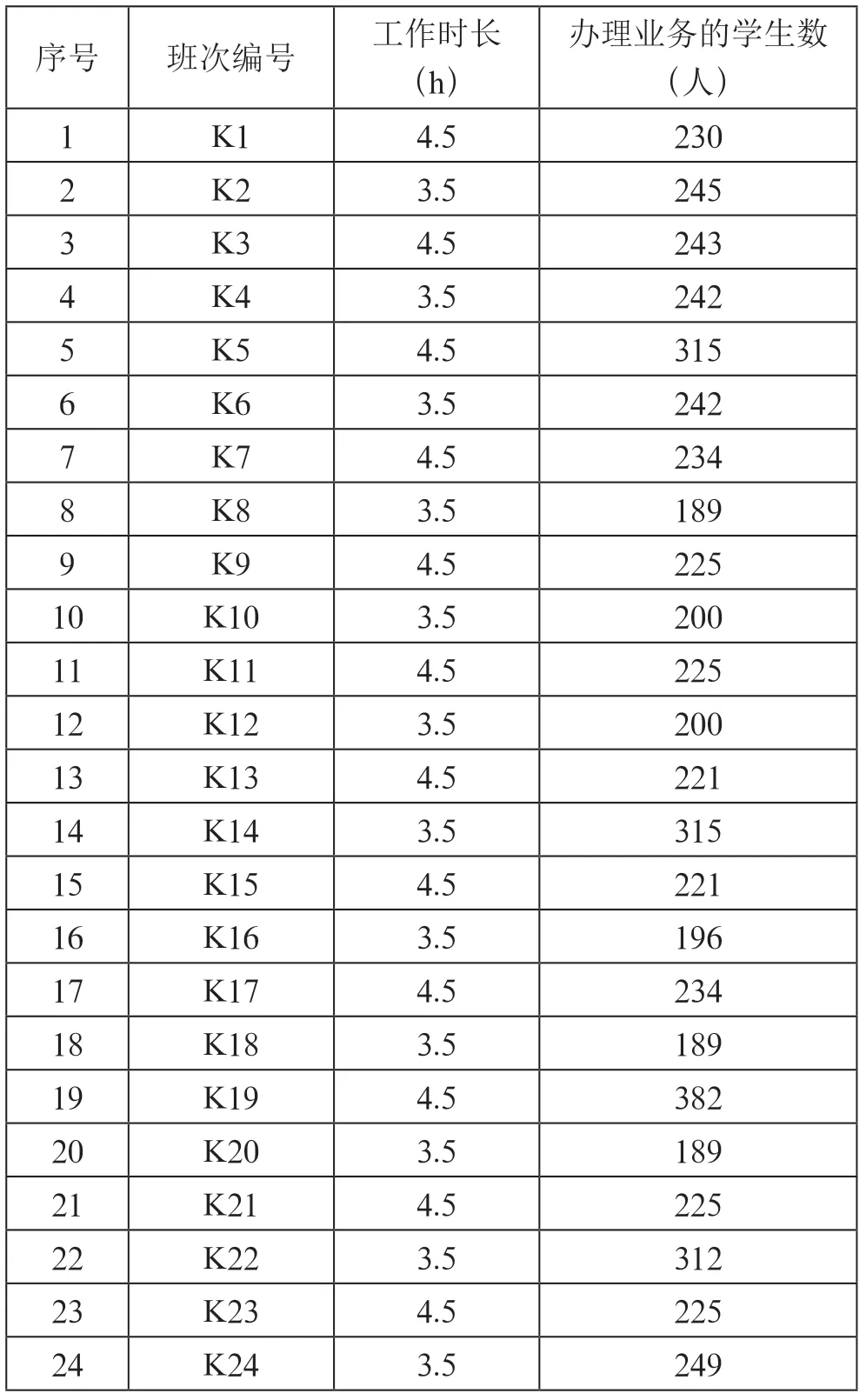
表3 24 个班次办理业务的学生数

2.2 模型效果评价

高校图书馆根据学生的各项需求，成立了信息服务中心、服务管理台等部门。但在后疫情时期，病毒传染路径存在复杂性和差异性，传统的排班会使得感染风险大大增加。因此，通过描绘各部门员工的网络图，基于图的平均顶点度，计算感染因子值以衡量感染病毒的风险，并将此作为该模型的效果评价指标。

员工网络图的顶点代表员工，边代表员工在同一部门至少在一起工作过一次。其中，G是第周的部门∈的网络图，每个图都有顶点集（G）和边集（G），设（）为网络图的每个顶点∈对应的度，R为部门∈在第周的感染因子，R为部门∈的感染因子值，部门∈在第周的感染因子计算公式为：

部门∈的感染因子值计算公式为：

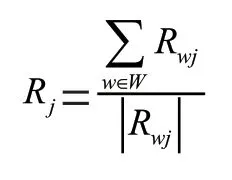
3 结果分析

3.1 数据分析

首先对一周24 个班次、8 个员工的算例进行测试，测试结果如图1所示。与优化前的排班方案如图2所示进行比较，优化后的最大工作时长为54 h，最小工作时长为37 h，最优目标值为166，大大降低了总成本。

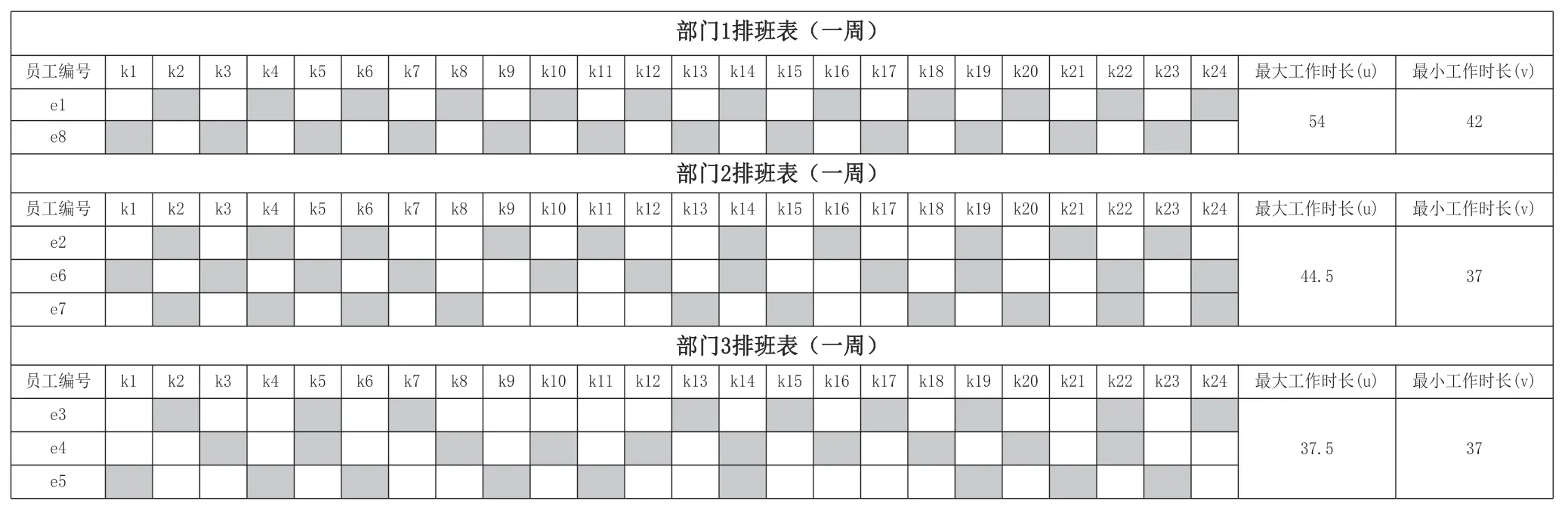
图1 优化后的排班方案

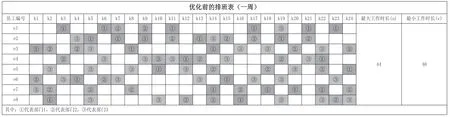
图2 优化前的排班方案

以一周的优化结果为例进行分析，优化后的排班方案的总成本比优化前明显降低，如表4所示。最大最小工时差（-）代表员工工作量分配是否均衡，浪费的人力成本代表员工有怠工的现象，惩罚成本是对未按时完成业务办理使得学生满意度降低的成本。

表4 优化前后成本对比

然后对连续两周48 个班次进行排班，可以得出如图3所示的排班方案，验证了该模型的有效性。

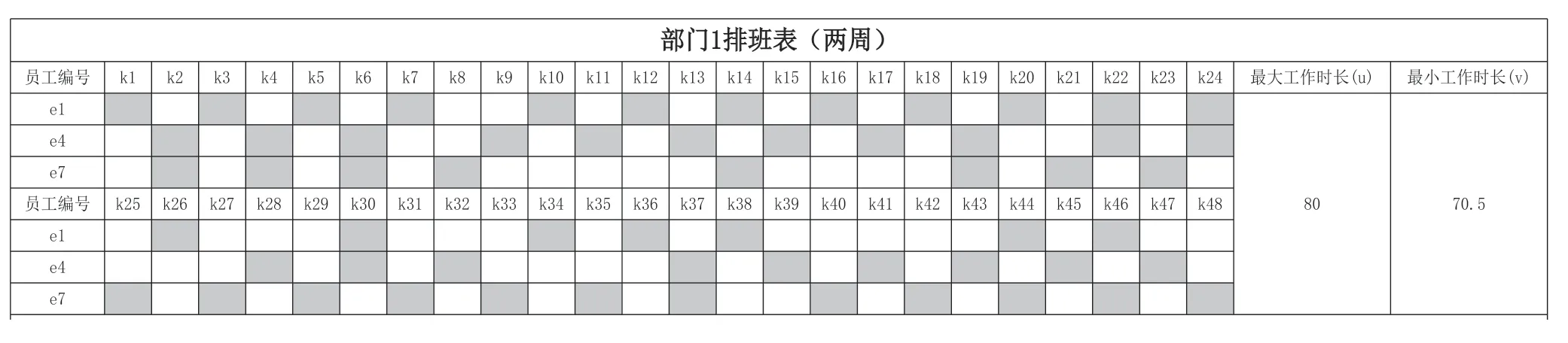
图3 优化后的两周排班方案

在优化前的排班中，员工可串部门轮班，不考虑交叉感染的风险，所以各部门的感染风险值相同。在优化后的排班中，为降低员工之间感染的风险则不允许员工串部门轮班，所以各部门的感染风险值不同。根据图4所示的员工网络图，计算出在优化前后各部门的感染因子值，如表5所示，优化后的各部门感染因子值小于优化前的感染因子值，说明优化后的排班方案不仅降低了成本，还降低了员工之间感染的风险。

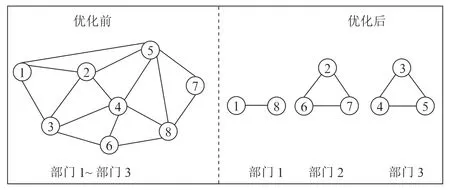
图4 员工网络图

表5 优化前后各部门感染风险值

3.2 灵敏度分析

3.2.1 员工数量对目标函数的影响

根据图书馆的规定，3 个部门最多招录共10 名员工，最少招录共8 人。在最少员工数为8 人的基础上，分别增加1 名员工和2 名员工，以原有8 位员工的平均工作效率作为增加员工的工作效率，得到了如表6所示的数据。结果显示当员工数量为9 人的时候，总成本最小。

表6 不同员工数量下的总成本

3.2.2 工作时长对目标函数的影响

在优化前的排班中，每个班次以4 h 为单位进行轮班。结合实际需要办理业务的数量与员工工作的灵活性，优化后的班次以4.5 h 和3.5 h 进行轮班，结果显示，优化后的班次使得总成本最小。如表7所示。

表7 不同工作时长下的总成本

4 结 论

（1）针对疫情常态化阶段的公共场所人员调度的问题，将感染因子作为模型的效果评价指标，来衡量员工之间感染病毒的风险，构建了以排班出现怠工现象导致的人力成本与不能达到服务水平要求的惩罚成本之和最小化为目标的人员调度优化模型，并用数学规划求解器GUROBI 进行求解。

（2）算例结果表明，本模型可解决图书馆工作人员的排班问题，能够实现在降低感染风险的同时还能使图书馆正常开放，验证了该模型的有效性。对影响目标值的两个因素（员工数量和工作时长）进行分析，得出了在员工数量为9时目标值最优的结论，同时验证了当前模型的工作时长更符合现实情况，使得总成本最低。

（3）GUROBI 求解器可在短时间内求解出该模型的最优解，但是在求解大规模案例（员工数量、班次数量等较多）时，求解时间过长。因此，在以后的研究中，考虑将求解器与智能优化算法相结合，提高大规模案例的求解效率。