基于低秩约束的多视角聚类算法研究

贺艳芳，李莉杰

（河南开封科技传媒学院 理工学院，河南 开封 475004）

0 引 言

聚类是机器学习中最重要的研究课题之一，其目的是在不知道样本标签的情况下，将样本分成不同的组，称为聚类。在当今时代，聚类技术在人工智能、数据挖掘和模式识别中占有重要的地位，通过聚类能够进行图像识别、数据的分类等。聚类技术属于无监督学习，利用数据之间内在结构技术，它是把相似的数据结构分为一类。多视角数据的特征包含了同一个对象不同角度的信息。例如：一个网页数据中有两个视角的数据既包含网页内容又包含网页链接信息，其中网页内容是一个视角，而网页链接信息是另一个视角；视频中包含音频、图像等特征；图像数据中既涉及颜色直方图特征、纹理特征等图像特征，又设计描述该图像内容的文本。多视图聚类就是将多个特征集聚成在一起进行聚类。由于这种方法解决了聚类的很多问题，所以多视图聚类算法已被广泛的使用和开发，以获得额外的信息，以改善最终的聚类。而在这些方法中，谱聚类方法因其定义明确的数学框架和易于实现而成为最流行的方法。目前常见的多视角方法可以分为以下几种方法：（1）协同训练方法；（2）多核学习方法；（3）多视图融合方法；（4）多视角子空间学习方法。协同训练算法在多视角算法中属于半监督学习方法，该算法只能解决两个视角的问题，当出现多个视角特征，用该算法会有局限性。它是通过训练两个视图中的两个分类器，这两个分类器进行分类，一起相互训练，两个视觉之间相互学习，不断迭代，直到信息一致。多核学习方法是将不同数据用多核表示，多视角数据通过多核框架，将多特征数据映射到高维空间，在高维空间构造组合空间，利用各个核的特征映射组合，在高维空间得到精确度更高的聚类结果。多视图融合方法，通过构建多视图亲和矩阵来进行聚类，一个视图用来约束另一个视图的相似度矩阵，通过强化不同视图的聚类来达成一致。大多数现有的基于图的聚类方法用图结构分离数据聚类。同时基于图学习的方法能更好地捕获数据空间的图结构。多视角子空间学习方法，学习目的从多视图中获得合适的子空间，这些视图生成一致性表示。

现实生活中的数据往往是多角度或多领域的，而传统的数据表示仅仅用一种数据表示，多数据的共性是有多个特征，使用多视角聚类算法能同时处理多特征数据。尽管这些多视角中的单个视角能充分完成聚类学习任务，但是结合不同视角的互补信息能减少任务的复杂性。由于稀疏表示和低秩约束利用不包含噪声的数据集且具有自表达的特性对数据点进行重建，即每个数据点能用其他样本点的线性组合来表示。本文研究前人的稀疏表示和低秩约束多视角算法，发现文献Elhamifar等人提出了使用稀疏矩阵表示的子空间聚类，该算法中的数据点和其他数据点之间是线性组合关系。文献LIU等提出的多视角子空间聚类算法，该算法用二维数据矩阵来描述系数之间的关联性，最终让数据构成的相关系数矩阵的秩达到最小。Kheirandishfard等人提出的DLRSC算法（Deep Low-Rank Subspace Clustering），该算法将低秩表示约束融入深度学习子空间聚类中，主要方法是将深度学习中的自编码器中间的单个自表达层替换成两个低秩自表达层，从而实现对自表达矩阵的低秩约束。该算法实验表明，基于深度学习的子空间聚类模型DSC往往可以更好地挖掘出数据之间的复杂结构，用更有的表示方法表述数据间的数据结构，为了最终获得更好的聚类效果。从以上多视角算法研究中，发现稀疏矩阵和低秩约束在多视角中占有重要地位。然而，主要的挑战是如何集成这些信息，利用稀疏矩阵和低秩约束提供一个融合兼容所有视图的解决方案。

1 低秩约束算法

构建一个功能强大，能有效描述数据点之间内在联系的图是当前多视图聚类算法实现的目标，基于图的半监督学习算法取得了良好的性能。当前较为火的基于图的构造算法中，低秩表示（low-rank representation, LRR）它可以同时探索数据的全局结构。因此，可以利用LRR学习到低秩系数矩阵来构建数据的近邻矩阵。除了传统的LRR模型，还有许多先进的方法，例如最近有人提出了变体。为了有效地探索结构信息的数据，郑等人施加局部表示系数的约束特征从而形成了局部的低秩代表约束（LRRLC）模型。

LRR中考虑一组样本=[，,…，x]∈R，LRR的目的是将数据中的每个样本表示为=[，，…，a]∈R，通过=，其中=[，，…，z]是一个矩阵，每个z和样本x的系数对应一个线性组合。因此在中每条记录都可以看成对于的x的重构。LRR算法能通过下面式子获得最小秩的解优化问题：

其中直接优化秩函数是NP难问题，很难求出该解。因此，我们通常使用跟踪规范（也称为核规范）。作为最接近秩范数的凸代理，它实现以下目标：

其中‖·‖*是某个矩阵的奇异值之和。考虑到样本通常是有噪声的或者缺失数据构成，LRR可以用一个更合理的目标可以表示为：

2 基于低秩约束的多视角聚类算法

子空间聚类算法被用于处理高维数据，它是机器学习中常用的聚类算法，而具有高维数据特征的数据在数据结构中较复杂。首先它将输入的数据特征映射到子空间的低维，其次在低维空间中，利用数据特征的不同，最后在子空间中把数据进行不同的聚类划分。从上面可以看出，基于子空间的聚类算法能把输入到不同子空间的数据融合在一起，子空间中聚类能够计算出子空间聚类的数目、数据的维度和每个子空间对应的基。由于子空间在处理高维度数据具有一定的优势，子空间被广泛用于图像的处理。

2.1 子空间聚类算法

给定数据矩阵∈R，子空间自表示特性可以表示为=，其中，为自表示系数矩阵，通过使用最小化矩阵的范数，求出的最优解，该解具有对角结构。求解过程可以由下列式子表示：

其中，‖·‖表示矩阵的范数，不同算法使用的范数不同，如在稀疏子空间聚类（SSC）算法应该采用范数。

2.2 基于核的低秩子空间聚类算法

基于子空间聚类算法，该文献[9]提出的算法是通过学习一个低秩核的映射，该核函数将数据从低维度空间映射到高维空间，在高维特征空间中具有线性子空间的结构。当高维特征子空间呈现线性结构时，数据对应的核函数()是低秩的。映射到高维特征线性子空间上，优化目标函数可以表示为：

其中：=(,)=()()表示未知的核Gram矩阵；是一个平衡参数。在这里，最优化‖()‖使得()是低秩的。可以将式（5）转为以下形式：

上述式（5）优化需要解决‖()‖的问题，因为上述式子过于依赖()。通过使用LEE等人提出的重参数，解决上述的最小的解。因为核矩阵是对称半正定矩阵，故可以把它分解成=，同时在该式子中，是一个方阵。可以得到以下式子：

利用‖‖来代替‖()‖，则目标函数表示为：

其中：()()=，在该式子中，假设数据点在离线性子空间距离很近，因此可以使用比较简单的核函数去定义。本算法的主要通过学习一个核矩阵=来解决问题。

3 基于深度学习的低秩多视角子空间聚类算法研究

3.1 深度学习算法

深度学习是当前学者研究的热点内容，它是以神经网络为基础，在对深层神经网络训练时，需要大量的数据和计算能力，当前研究者主要研究卷积层的深度学习框架。主要的深度学习框架有AWS亚马逊MXNet，谷歌的Tensorflow，Facebook的PyTorch等，上述的框架都是利用稠密矩阵乘法实现卷积计算。

将深度学习引入到多视角模型中，可以使用合适的自表达关系。深度学习在算法中能更深层次挖掘数据之间的关系。通过挖掘出比较好的数据自表达方式，提高聚类性能。

3.2 深度低秩多视角子空间聚类

为了向自表达矩阵中添加低秩表示约束，通常是直接在目标函数中增加自表达矩阵的核范数正则化‖‖。但是在反向传播算法中，这种方法不适用。因为难以计算出核范数约束的梯度，让这一方法变得困难。为了解决这个问题，通过在该文在提出的DMSC算法中添加秩约束rank()≤来解决。可以由以下式子解决：

4 基于低秩约束的熵加权多视角模糊聚类算法

针对当前基于K-means的多视角模糊聚类算法研究中存在的问题，文献[13]提出的一种基于低秩约束的熵加权多视角模糊聚类新方法。它主要通过向多视角模糊聚类算法的目标学习准则中引入低秩约束项，在整体上控制聚类过程中各视角的一致性；另一方面由于所有视图都被平等对待，在这些方法中没有考虑每个视图的差异基于香农熵理论，通过熵加权机制来控制各视角之间的差异性。

设多视角隶属度,…,，融合成为一个隶属度矩阵，将矩阵的秩函数凸松弛为核函数，在矩阵中进行低秩约束，可以将多视角数据之间的一致性问题转为核范数最小问题进行求解，具体定义为：

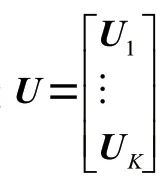
其中约束条件为：

以上算法是在k-means算法的基础上进行研究，该算法的优点对噪音跟离群点比较敏感。由于在高维数据的情况下，数据点的距离相近，使用欧式距离无法测量数据点的关系，故该算法也不能解决高维数据的问题。虽然利用低秩约束的子空间聚类能够解决高维数据的问题，但是利用K-means算法的多视角聚类在结构上具有一定的优势，它能够构建多视角的隐式结构，能够充分利用多视角数据的互补性，同时在K-means算法的基础上利用低秩约束和稀疏约束算法，能解决解决数据的局部结构和稀疏结构问题。

5 结 论

在将来的工作中，我们会将低秩约束融入多视图聚类算法中，融合多视图不同的相似矩阵，同时会研究由于多视角数据集在收集过程中导致数据的丢失即不完备数据，设计新的算法处理不完备数据。同时针对大数据，进一步研究在大数据背景下，多视角聚类的算法。