天线面板数字化展开建模技术及其应用

甘忠，蒲理华，凌子昊，石望兴，马博宇

（1.西北工业大学 机电学院，陕西 西安 710072；2.中国空间技术研究院西安分院，陕西 西安 710000）

0 引 言

针对天线雷达曲面的三维设计展开转换成二维CAD图纸同时展开精度小于1 mm的设计。由高斯曲率可知，该天线曲面为不可展曲面，对于此类不可展曲面的展开，在工程应用中通常对模型结构进行多次重复的修改、缝合，然后得到达到设计要求和精度使用要求的二维CAD图纸；也可以用牛皮纸去贴合三维实体表面，将牛皮纸分片拼接，即可得到二维平面图，获得相应图纸。这两种方法都属于传统方法，时间和人力成本相对较高，同时得到的二维平面图精度低，而且人工方法很大程度上取决于工人经验。

AZARIADIS等人提出了一种基于约束全局优化的任意三维曲面平面展开生成方法，这种方法可以导出初始平面展开图，并对其进行细化，以满足某些标准。这种优化被描述为约束下的全局极小化问题。Zhong等人介绍了一种新的方法，通过打开每个翼形三角形对的弯曲形状，从三维三角化曲面生成二维平面图案。Liang等人提出了一种双曲面展平的有效方法，用于展平自由曲面的三角剖分面。徐石磊等人提出了用混合网格等面积几何模拟展开法确定不规则边界曲面零件毛坯外形。詹雯等人提出了一种基于几何展开/力学修正的复杂曲面展开的通用算法实现复杂曲面的展开。Kolmani等人提出了一种新的基于分治策略的曲面重构与展平快速算法。可展条纹用于逼近曲面，这样可以快速展平曲面，且不会产生任何变形。Li等人提出了一种使用质量弹簧模型的有效展平算法。在质量弹簧模型中，引入了交叉弹簧以减少所得表面的变形。使用三角形条带可以加快平面显影过程。

本文针对热控多层三维设计展开转换成二维CAD图纸，运用CATIA创成式外形设计和有限元分析模块，提取曲面以及相应的三角网格，再采用优化的几何展开算法展开，得到满足精度的展开平面。

1 曲面生成

针对热控多层模型可知，整体雷达曲面紧贴在筋条处，要将整体曲面展开很复杂，甚至出现展开畸变，因此提出采用分片进行展开，按筋条区域进行划分，得到多片曲面，展开后将多片曲面缝合，贴在筋条上。

利用CATIA的创成式外形设计模块中的提取功能选择筋条内边线。如图1所示。选择要提取的筋条边，完成筋条的边线提取。

可选择拓展类型有：

（1）点连续：提取的元素将没有任何孔。

（2）切线连续：将根据相切条件创建提取的元素。

（3）曲率连续：针对曲线特征根据曲率条件创建提取的元素。

图1 筋条边线提取

利用CATIA的创成式外形设计模块中的填充功能，选择要形成封闭边界的曲线或曲面边线。如图2所示。选择上述提取的筋条边线，完成轮廓封闭，生成复杂曲面。

图2 曲面填充

任意选定的支持曲面和填充曲面之间的“连续”类型。有以下几种连续类型可用：点、相切、曲率。“偏差”复选框可输入填充当前间隔的值。确定后，生成要展开的曲面。

2 曲面模型三角化

点击CATIA分析与模拟功能中的Advanced Meshing Tools模块，将曲面三角化处理。如图3所示。为三角网格划分过程，需要制定以下参数。

图3 曲面三角化

网格尺寸：指定网格元素的大小。

绝对弦高（Absolute sag）：网格与几何图形之间的最大间隔。

元素类型（Element type）：可以选择所需的元素类型（“线性（Linear）”或“抛物线性（Parabolic）”）。

将网格以dat文件格式导出。得到曲面的三角网格形式。

3 展开算法

采用改进的等面积几何展开法，整个过程分为四个部分：展开基点的确定、基点相邻点坐标确定、待定节点坐标确定、边点的确定。

3.1 展开基点的确定

曲面三角化的模型内各个顶点按照角度加权更新依次展开到平面上，从而空间节点得到展开。对于三角网格边缘角点，根据面积不变原则进行展开。

基点的展开是选择曲面网格的第一个点，选择不同的网格节点作为基点， 展开的效果会有不同，展开的精度也会不同， 因此基点的选择就显得十分必要了。它会影响节点的展开效果。

选择基点参考以下原则：

（1）对称曲面，基点尽量选择对称中心点或附近节点。

（2）在曲率较大范围内选择基点。

在实际选择时，通常会根据经验选择基点，根据曲面三角网格的面积、结构长度、表面角度等结构尺寸进行综合评估，最终确定基点。

3.2 基点相邻点坐标计算

基点通常被多个单元所共有，但按照展开前后面积不变和相邻角度加权的原则，得到基点相邻节点的平面展开坐标。如图4所示，以此例说明此算法。

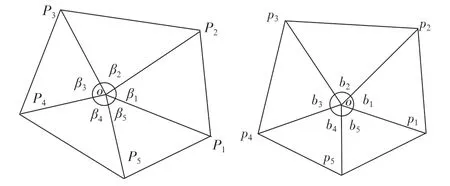
图4 展开图例

空间三角网格角度和：

展开平面夹角和：

展开前后角度的增加值为：

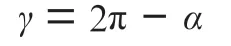
将按权值分给展开平面的每个夹角：

记伸缩率为：

依据展开前后面积相等的原则：

结合上述公式可得：

将值带入分别得到展开的边长。将点坐标定为（0，0）点，进而得到相邻点的坐标，则：空间点的展开点的坐标为(||,0)为，空间点的展开点的坐标为||cos,||sin)，空间点的展开点的坐标为(||cos(＋),||sin(＋))，空间点的展开点的 坐 标 为(||cos(＋＋),||tsin(＋＋))，空间点的展开点的坐标为(||cos(＋＋＋),||sin(＋＋＋))。

3.3 外圈点展开

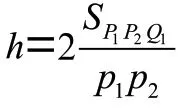
3.4 边点的确定

遍历曲面网格的节点以及节点连成的边线，当线段为两个三角共有，则标记为内边线，反之为外边线，同时获得轮廓节点。

图5 展开图例

展开的整体流程算法为：

输入：空间三角网格节点坐标。

输出：平面网格轮廓坐标。

Step1：选择曲面三角网格的展开基点。

Step2：遍历基点相邻的节点以及节点和基点线段长度，将其展开，标记基点、相应的边、三角面片为已展开。

Step3：遍历下一圈相邻节点，先展开上一圈节点边线对应的节点。在按相同方法展开其余节点。将展开的节点、边线记录为已展开。

Step4：依次按照step3进行遍历展开到平面，标记相应的点、边、三角片为展开，记录已展开顶点数目；如果展开顶点数目不等于曲面模型中的顶点数重复step3。

Step5：如果边线只有一个三角形共有，则这条边线为轮廓边。根据这一条件遍历网格边线和三角网格，提取出网格边线，获取边缘展开节点坐标，获得轮廓。

Step6：展开结束。

4 展开算例

本文采用上述CATIA提取、填充生成的复杂曲面为例来验证展开算法的有效性。待展开曲面如图6所示。

图6 待展开曲面网格

最终展开网格图形如图7所示。

图7 展开网格平面图

由表1可知，边界最大误差小于1 mm内，满足设计要求的展开效果，课件算法是可行的。

表1 测量值和展开值面积对比

5 结 论

本文基于热控多层三维设计展开转换成二维CAD图纸同时展开精度小于1 mm的设计需求，提出了一种优化的基于CATIA环境下几何展开复杂曲面通用算法的方法，并开发出了相应的系统。实现复杂曲面的任意展开，获取到了满足设计要求的展开效果，降低了研制时间，减少了生产成本。