典型抗量子公钥加密算法实现

◆喻文韬

（东南大学网络空间安全学院 江苏 210023）

1 绪论

量子计算机的概念是最早是由英国牛津大学物理学家David Deutsch 和美国科学家Richard Feynman 于20 世纪80 年代共同提出。量子理论中定义了一个粒子同时可具有数个不同状态。若我们采用这种具备不同状态的粒子进行数学运算，那么在同一时间就可以完成对多种状态的结果的运算。假设采用1 个粒子就可以表示0 和1 两种不同状态，那么采用128 个这样的粒子就可以完成在同一时间计算出2128种状态的结果。

量子计算机一旦现世，其计算量与现在市面上存在的超级计算机的计算量完全不在一个数量级，因此现代密码体系中的各种加密算法如RSA 公钥加密算法（基于大整数分解数学问题的困难性），ECC公钥加密算法（基于椭圆曲线的离散对数问题）完全可以采用量子计算机来进行暴力破解，现代密码体系的安全性即将遭受重大威胁。

简单来说，这是因为量子计算机能够帮助黑客更快闯过算法陷门这道难关。与各个比特只能处于1 或0 状态的经典计算机不同，量子计算机可以使用能够同时代表1与0的多种可能状态的量子比特——这就是所谓叠加现象。另外，通过所谓纠缠现象，各个量子比特之间也能够在远距离条件下相互影响。

在这些现象的作用之下，只需要添加少数额外的量子比特，我们就能够让计算机的处理能力呈指数级上升。拥有300 个量子比特的量子计算机就可以表达比可观察宇宙中全部原子总数更多的值。假设量子计算机能够克服其自身特性带来的某些固有限制，那么其最终完全有可能在相对较短的时间之内测试加密密钥的所有潜在排列。

抗量子加密是一种新的加密方法探索方向，其能够利用现有经典计算机实现，但却具有足以抵御未来量子攻击的能力。其中一种防御方式在于进一步增加数字密钥的大小，以便持续提升黑客利用算力进行暴力破解时所需要搜索的总体排列数量。举例来说，如果将密钥的大小从128 位加倍至256 位，将能够快速增加使用Grover 算法时量子计算机所需要搜索的全部可能排列数量。另一种方法则涉及更为复杂的陷门函数，这意味着即使是像Shor 这样的算法也很难帮助量子计算机成功破解密钥内容。研究人员正在探索各种各样的方法，包括基于格子的密码学以及超奇异同构密钥交换等相当新奇的实现途径无论具体方法如何，新方法的目标都在尝试将一种或者几种能够广泛采用的方法归为一类。美国国家标准与技术研究院于2016 年启动了一项流程，旨在制定政府使用的后量子加密标准。其目前已经将最初的69 个提案缩小至26 个，并表示初步标准草案可能会在2022 年前后正式公布。由于加密技术需要被深深嵌入众多不同的系统当中，所以标准制定面临着巨大的压力，找到可行途径并实现新的技术也可能需要投入大量时间。去年，美国国家科学院研究报告指出，以往业界花了十多年时间才全面推出一种能够广泛部署的加密方法——但其中仍然存在缺陷。考虑到量子计算的发展速度，我们的世界也许已经没那么多时间用来应对这一波新的安全威胁。

2017 年5 月3 日，世界上第一台光量子计算机诞生。这台计算机是真正“中国制造”，它是由中国科技大学、中国科学院-阿里巴巴量子计算实验室、浙江大学、中国科学院物理所等单位协同完成研发。2020 年12 月4 日，中国科学技术大学宣布该校潘建伟等人成功构建76 个光子的量子计算原型机“九章”。“九章”是中国科学技术大学潘建伟团队与中科院上海微系统所、国家并行计算机工程技术研究中心合作，成功构建76 个光子的量子计算原型机，求解数学算法高斯玻色取样只需200 秒。这一突破使我国成为全球第二个（第一个为IBM的Q System One）实现“量子优越性”（国外称“量子霸权”）的国家。

2 NTRU 加密算法原理

在量子计算机现世之后仍能够保持机密性而不被其暴力破解，即能够抵御出破译依旧存活的密码称为后量子密码（Post-Quantum Cryptography）。NTRU（Number Theory Research Unit）加密算法便是后量子公钥加密算法中最为典型的算法。

20 世纪90 年代，美国的三名数学家及密码学家J.Hoffstein，J.Pipher 和J.H.Silverman 共同首先提出了NTRU 公钥加密算法。NTRU 公钥加密算法不仅能够抵御可能出现的量子计算机的暴力破译，而且在密码算法所基于的数学问题上比现在市面上大多数采用的RSA 及ECC 椭圆曲线算法更难以破解。从现阶段的研究来看，NTRU公钥加密算法所基于的数学困难问题是难以被量子计算机所暴力破解的。不仅如此，在加解密的速度方面，NTRU 因为流程相对简单，步骤简洁，其运算速度比现有的大多数加密算法更胜一筹，公钥系统也相对容易实现。总的来说，我们有理由相信后量子公钥加密算法（NTRU）完全有可能在未来的公钥密码体系中占有主导地位。

1.1 NTRU算法参数

NTRU 公钥加密算法中的关键参数为三个整数参数（N，p，q），以及四个N-1 次整数系多项式的集合。该算法的加密以及解密过程均是在多项式截断环R=Z[X]/（XN-1）上运算。对于整数p 和q，他们不需要是素数，但必须满足gcd（p，q）=1，且q 必须远远大于p。我们设：L（d1，d2）意味着对于多项式F 属于R，多项式中共有d1个系数为1，d2个系数为1，则剩余的系数均为0，可以得到以下多项式的集合：

1.2 密钥的生成

在NTRU 公钥加解密的过程中，绝大部分的运算都是发生在多项式截断环R=Z[X]/（XN-1）上。通过了解该加密算法的加解密流程，我们可以得知加密时需要用多项式h 和多项式r 想乘，而在解密时需要用私钥f 与密文多项式e 相乘得多项式a，且还原明文时会用到私钥f 模p 的逆Fp与多项式a 相乘得到解密后得明文m 我们不妨设私钥f 多项中系数-1 和系数+1 的个数相等均为d，这样在使用扩展欧几里得算法时就可以很简单的得出私钥f 模p 的逆 Fp=1。通过设置私钥f 的多项式中正负一系数的个数就可以提高NTRU 加密算法的运算速率。

我们随机生成两个次数不高于N-1 次的多项式f 和g 分别属于Lf和Lg，Fp，Fq分别为多项式f 模算法参数p 和q 的逆。我们需要用扩展欧几里得算法来对Fp和Fq是否存在进行验证。

对于扩展欧几里得算法：

设存在整数a，b，则一定存在整数x，y 满足：

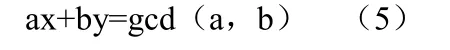
当b=0 时存在x 与y 为最后一组解，而每一组的解均可以根据最后一组求得。所以第一组的解x与y必定存在，这时可用递归算法，求得b=0 时返回x=1，y=0。再根据x1=y2，y1=x2-k*y2 可得当层的解，由此不断返回可得原解。

将整数a，b 扩展为多项式则可以得到

设存在多项式a（x），b（x），则一定存在u（x），v（x）满足

在这种前提下，我们不妨设私钥多项式f 为a（x）且b（x）=（xN-1）=（x-1）（xN-1+xN-2+……+x+1）代入即可算出第一层的多项式为私钥f 模p 和q 的逆元。

在此的基础上我们可以合理推测，若存在gcd（f，xN-1）=1 mod 2；

那么也就存在多项式u（x）与多项式v（x），满足：

其中多项式u（x）即为私钥f 在多项式截断环Z2[X]/（XN-1）求出的逆元。

随后我们可以将私钥f 在多项式截断环Z2[X]/（XN-1）上的逆元一步步提升模的数值，使得最后提升至模q。且由于Fq是私钥f在模2 情况下的逆元，即Fq*f=1 mod 2。

对于Fq*f=2k+1，进行赋值并带入新的私钥，进行如下运算：

即可计算出私钥f 模4，16，256 等数值的逆元，由由于q 一般选为2n，则可以推出若私钥q 模2 存在逆元，那么模q 一定也存在相应的逆元。

综上可得公钥为多项式h（x）=Fq*g mod p，私钥为多项式f（x）。

1.3 明文加密

先随机产生一个明文消息多项式m（x），该明文多项式属于Lm，且该明文系数不超过N-1 次，随后随机产生一个多项式r（x），且该r（x）多项式次数不超过N-1 次。随后进行计算e（x）=h（x）*r（x）+m（x）mod q，计算出的多项式e（x）则为明文加密之后产生的密文。

1.4 密文解密

在得到密文多项式e（x）后，我们用私钥f 进行计算得出多项式a=f*e mod q，随后计算 Fq*a mod p 计算值得到明文m。

多项式a 其系数需要限制再区间[-p/2，p/2]内，因此这个多项式在所有参数模q 的情形下都不会改变，即可得正确的密文解密。

3 NTRU 算法具体实现

量子计算机的发展，对目前广泛应用的RSA、ECC 等公钥密码体制构成了严重的威胁，面临量子计算机的挑战，国际上掀起了抗量子计算公钥密码的研究热潮。一种方案是采用量子密码、DNA 密码等基于非数 学难题的新型密码。这些极具潜力的新型密码的研究还处于初级阶段，有待我们深入系统地研究完善。另一种方案是采用基于数学难题的、能够抗量子计算攻击的密码。基于量子计算机不擅长计算的数学问题构造密码，便可以抗量子计算的攻击。

3.1 公私密钥生成

在生成NTRU 的公私密钥时，我们需要先进行参数选择，方便起见已将df，dg，dr 都定义为d。

void KeyGeneration（int Lf[]，int U[]，int g[]，int h[]）函数为密钥生成函数。通过输入的Lf，U，以及多项式g，来生成私钥f，公钥h。要保证私钥f 多项式中系数-1 和1 的个数相同，则f*Fq=1 mod 2。

在NTUR 算法原理中可以得知若f mod 2 的逆元存在，那么f mod q 的逆元必定也的得出。因此在密钥生成函数中需不断提高f 模的值大小来完成密钥生成。

3.2 明文加密过程

void Encryption（int h[]，int Lr[]，int m[]，int e[]）通过该函数我们可以实现对输入明文消息多项式m 的加密。通过具体的e=r*h+m mod q 算法得到密文e。

3.3 密文解密过程

void Decryption（int e[]，int Lf[]，int a[]，int Fp[]）通过该函数可以实现对加密后的密文e 的解密。在运行该函数时我们首先需要先进行a=f*e mod q 运算，并且使得该多项式系数位于[-p/2，p/2]之间，随后计算a mod 结果得明文m。

3.4 实现界面

选取参数N，p，q 分别为11，3，32，加解密结果如图1 所示。

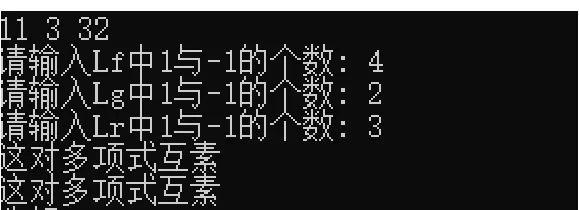
图1 输入关键参数

以下分别为公钥、私钥、明文、密文以及解密后得到的正确明文。

图2 公钥

图3 私钥

图4 明文

图5 密文

由图6 可以看出成功进行了明文的加密以及密文的解密。

图6 解密密文得到的消息

当我们选择了不互素的多项式Lf，Lg 和Lr 时则会出现图7 结果。

图7 输入多项式不符合要求

4 总结

对于多项式模运算中的求逆元运算，直接选择模q 运算较为困难，代码实现起来也很复杂，会使得密钥生成的速度不够快捷，因此可以选择从模2 求逆一步步提升到模q 求逆元（q 取值一般为，n 为正整数），这样使得密钥生成能够更为快捷的完成，提升了整个算法实现的高效性。

对于截断多项式环上的多项式运算，直接在外部进行运算是比较耗费时间的，因此将环R=Z[X]/（XN-1）上的两个多项式运算（例如多项式模加，模乘以及模逆运算）直接分解为具体的功能函数，从而简化了算法具体加解密实现的流程，体现了该算法实现的高效性。

NTRU 加密算法并不是十全十美的，它依旧存在着解密错误的问题。通过不断选择合适参数测试出错概率，可以看出参数N，q 均对于解密的成功性具有一定影响。在具体代码实现NTRU 加解密的过程中，由于我个人能力的不足，编程水平有限，并不能够特别明显优化该算法的实现过程，但我相信，随着人们对于该领域不断探索学习，未来一定会出现更为高效的加解密实现方式。对于典型后量子公钥加密算法中的NTRU 加密算法具备着重大的潜力，并且能够抵抗量子计算机的量子分析，未来一定会成为公钥加密算法体系的一大热点。