古城墙本体内雨水入渗特征的影响研究

2022-10-14刘晨辉祝彦知李新明任克彬

中原工学院学报 2022年4期

刘晨辉，祝彦知，李新明，任克彬

(1.河南省文物建筑保护设计研究中心，河南郑州 450002； 2.中原工学院建筑工程学院，河南郑州 450007；3.河南省文物建筑保护研究院，河南郑州 450002)

降雨是诱发边坡失稳的重要因素，多数边坡失稳发生在降雨期间或降雨之后的一段时间内。土质城墙结构、形态与边坡相似，同样面临降雨诱发失稳的风险，城墙的破坏将会对人类文化遗产保护与传承带来严重威胁[1,2]。古城墙长期处于非饱和状态，降雨期间，雨水沿城墙表面渗入本体，尤其是城墙表层土体松散，降雨入渗更加明显。雨水入渗导致城墙本体含水率上升，基质吸力下降；根据土的非饱和剪切强度理论，基质吸力的降低将导致城墙潜在滑动面抗剪强度不断降低，造成城墙失稳破坏[3]。

非饱和土质城墙本体是一种复杂的三相土，雨水在城墙本体内部的运移是一个动态变化过程[4]。近年来，众多学者研究水分在土体包气带中的运动规律，取得了丰富的成果。韩同春等[5]研究了降雨入渗率与降雨强度间的变化关系，揭示了入渗对双层土边坡的破坏机制；张社荣等[6]结合强度折减技术进行了瞬态渗流作用下的边坡稳定性计算；Anastasia等[7]探讨了利用土体空间变异分析方法计算非饱和边坡在降雨期间的稳定性；石振明等[8]提出了多层非饱和土边坡在降雨入渗过程中的稳定性分析方法；赵金刚等[9]探讨了填方边坡在降雨蒸发循环作用下的变形特征，分析了其演化规律与诱发机制；吴长富等[10]根据实际气象资料，利用非饱和土力学理论，研究了降雨作用下水分运移对边坡稳定性的时间及空间效应。已有研究中对降雨作用下边坡及路堤内水分迁移和稳定性的变化机制及工程应用进行了深入探索。其中对降雨强度、降雨历时两种降雨要素的研究成果最为丰硕，但对入渗表面对入渗速率及入渗量的重要影响研究不多。与边坡、路堤相比，城墙有更大的入渗表面，包括顶面以及两侧坡面，如图1所示。因此，考虑城墙特有较大入渗表面等结构特征的影响，分析城墙本体降雨入渗机制及稳定性具有重要意义。

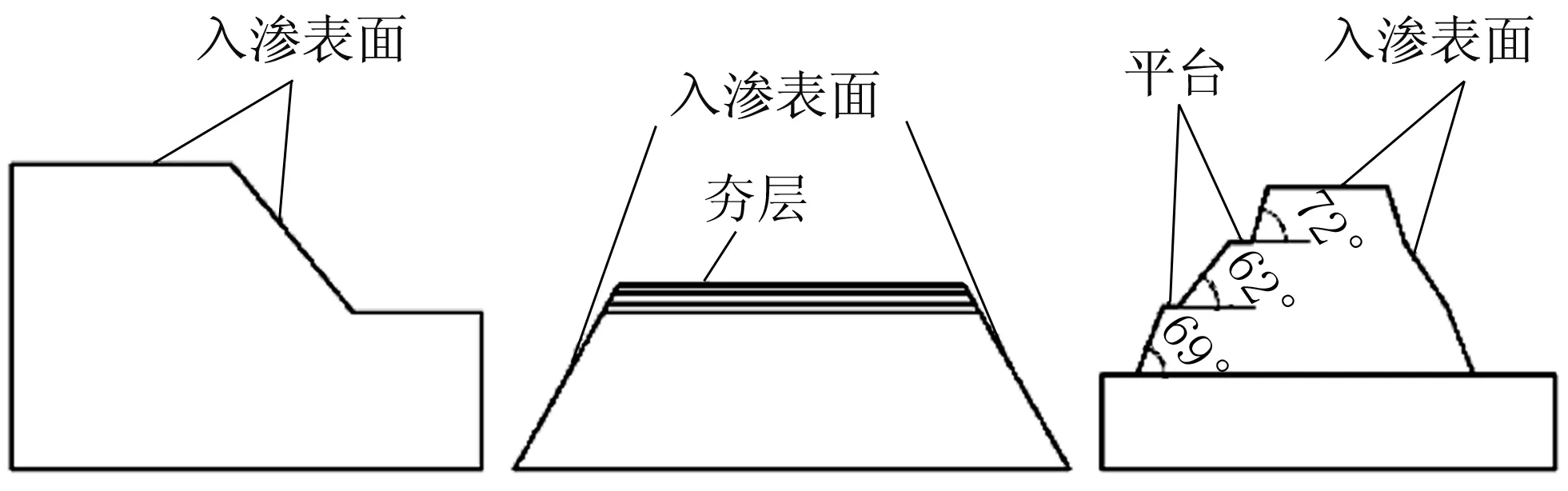
(a) 边坡 (b) 路堤 (c) 城墙图1 降雨入渗表面Fig. 1 Rainfall infiltration surface

本文以河南省新郑市郑韩故城城墙遗址为背景，利用有限元软件ABAQUS，分析了不同降雨要素下，古城墙遗址特有的较大入渗表面结构特征对城墙本体孔隙水压力、速度矢量场以及饱和度变化的影响；并探讨了城墙坡面、平台对城墙本体内水分入渗作用的影响，研究成果可为揭示降雨诱发城墙失稳机制提供依据。

1 水分运移基本方程

降雨作用下的城墙本体渗流场分析中，降雨入渗形成的水分运移可概括为城墙剖面上的瞬态非饱和渗流场，此过程遵循达西定律和质量守恒定律。

1.1 非饱和土达西定律

1931年，Richards将达西定律推广解决非饱和液体流动问题，其中考虑了渗透系数与吸力或吸力水头之间的影响。非饱和土中水分运动的方程可表示为[11]：

(1)

式中：θ为体积含水率；hm为基质吸力水头；kx(hm)、kz(hm)分别为x、z方向上以土体体积含水率和基质势为自变量的非饱和渗透系数函数。

1.2 质量守恒原理

质量守恒原理是指对于一个给定的土体单元，水的损失或补给率是守恒的，等于水流入与流出土体单元的净流量。质量守恒原理也称连续性原理。由此可得：

(2)

式中：Vwx为水平水分通量；Vp为竖直水分通量。此式是土中水分非稳定渗流或瞬态渗流的控制方程，既适用于饱和土也适用于非饱和土。

1.3 瞬态非饱和渗流

根据质量守恒原理，将式(1)代入式(2)，可得二维单元体内降雨入渗的非饱和土质城墙入渗的偏微分方程：

(3)

式中：z坐标方向附加的一项是由位置水头引起的。

1.4 土水特征曲线与渗透系数曲线的描述

在饱和非饱和渗流数值计算中，城墙本体的渗透系数与其断面的饱和度、孔隙水压力的分布及大小相关。土体体积含水率和孔隙水压力的关系即为土水特征曲线，这是描述非饱和土强度与渗透系数的重要工具；将渗透系数与孔隙水压力联系起来即为渗透系数曲线[12-14]。模型中土水分特征曲线与水力参数的函数关系为：

(4)

(5)

式中：θ是体积含水率；θr是残余含水率；θs是饱和含水率；Ks是饱和渗透系数；a、m、n是土水特征曲线形状参数；φ是基质吸力。

2 计算模型、参数及方案

2.1 计算模型

模型范围的大小对有限元计算，尤其是渗流场计算有较大的影响。根据郑颖人等关于边坡模型的研究[15]，结合城墙模型，将墙脚至模型边界的距离取为城墙高度的2倍，且模型上下边界的高度不低于2倍的城墙高度。

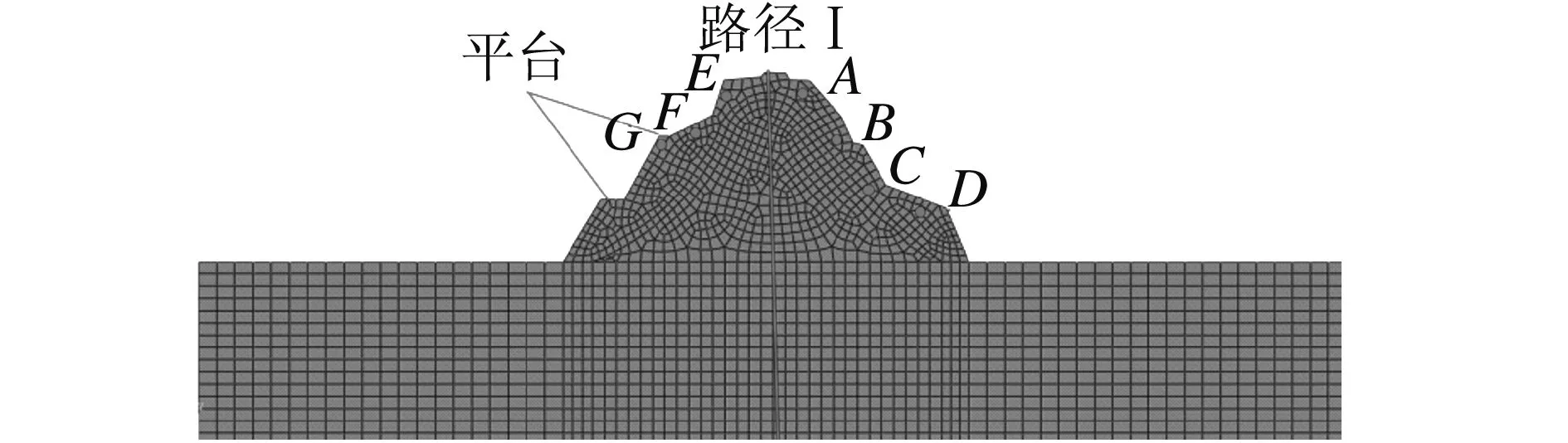
图2 有限元计算模型Fig. 2 Finite element calculation model

图2所示为郑韩故城北城墙段的一个典型剖面计算模型，计算网格单元数量为1 904，节点数量为2 015。从计算模型中可知，城墙本体的降雨入渗表面为整个城墙外表面轮廓，与边坡、路堤相比，较大入渗表面意味着更多的入渗量，这对整个城墙剖面内雨水运移产生较大影响。此外，外界环境造成城墙表面特有的多平台，坡面也会加剧本体内各个位置间较大的渗流差异。

由于模型区域较大，选取特征点以及特征路径量化城墙本体孔隙水压力及渗流速率等的变化规律。其中，特征路径Ⅰ是从城墙最高处沿竖直方向到模型底部；特征点A、B、C、D的高度依次为14 m、9.05 m、5.77 m、3.96 m；特征点E、F、G则依次位于模型左侧不同坡角(71.7°、25.7°、0°)的城墙表层土体部位。

2.2 计算参数、初始条件

(1) 计算参数。根据《土工试验方法标准》(GB/T 50123-2019)，通过变水头渗透试验法，计算得到该城墙段的饱和渗透系数平均为5×10-6m/s。由于城墙本体内各位置的渗透系数由基质吸力与初始含水率共同决定，根据非饱和土力学理论，通过Van-Genuchten模型进行拟合，求得城墙土的土水特征曲线(SWCC)，见图3；土体渗透系数同样利用Van-Genuchten渗透系数模型拟合试验所得如图4所示。

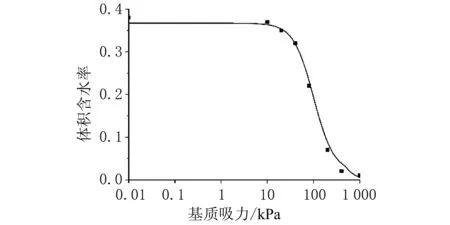
图3 土水特征曲线图Fig. 3 Soil-water characteristic curve

图4 渗透性函数曲线图Fig. 4 Permeability function curve

(2) 初始条件。地下水位于地表以下10 m处，城墙上表面初始孔隙水压力为-264.7 kPa。图5所示为城墙剖面路径Ⅰ上初始孔隙水压力随高度的变化规律。

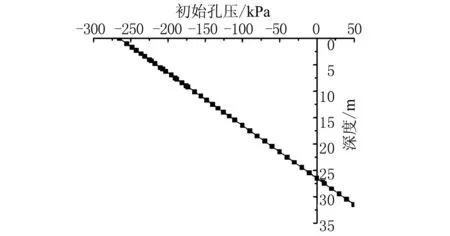
图5 初始孔隙水压力分布图Fig. 5 Initial pore water pressure distribution

(3) 边界条件。将降雨强度转化为表面流量边界施加于模型表面。当降雨强度不大于土体的渗透系数时，按照降雨强度设置流量边界；当降雨强度大于土体渗透系数时，将在城墙表面形成径流和积水，此时的流量边界按照饱和渗透系数设置[3]。

2.3 计算方案

受城墙较大入渗表面影响，研究城墙内部水分运移规律对不同降雨要素的响应是十分必要的[16]。依据降雨强度，降雨历时，设置如表1所示3种降雨方案对城墙降雨入渗过程进行数值模拟。

表1 降雨强度分布和参数设计

3 计算结果与分析

3.1 城墙孔隙水压力

降雨作用下，城墙稳定性受多重因素影响，其中基质吸力降低甚至形成正孔隙水压力，会造成土体有效应力降低，威胁城墙本体安全。鉴于此，将降雨强度按照节点流量施加于模型表面，分析城墙本体内不同位置特征点在上述3种降雨方案下的变化情况，揭示城墙孔隙水压力在降雨作用下的变化规律，结果如图6所示。

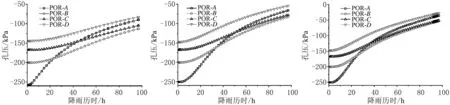
(a) 方案一(降雨强度0.05Ks) (b) 方案二(降雨强度0.1Ks) (c) 方案三(降雨强度0.2Ks)图6 特征点A-D孔隙水压力随降雨历时的变化Fig. 6 Variation of pore water pressure at characteristic points A-D with rainfall duration

特征点A、B、C、D分别位于城墙剖面从上到下不同高度处，各特征点位置受地下水、自然环境等因素影响差异较大。从图6可以看出，初始孔隙水压力(绝对值)随高度的增加逐渐增大，含水率逐渐减小。降雨历时96 h后，D点基质吸力最小。分析可知，初始基质吸力越小，渗透系数越大，同时受入渗面积较大影响，雨水在初始基质吸力较小的位置快速入渗，孔隙水压力显著增大。此外，在任一降雨条件下，城墙表面基质吸力(绝对值)随降雨历时的增加而降低，直至0 kPa，即饱和状态。具体表现为：同一降雨强度下，初始基质吸力较大的城墙表面，其孔隙水压力上升速率快于初始基质吸力较低的城墙表面。

同一基质吸力条件下，相同降雨历时的城墙表面孔隙水压力上升幅值随降雨强度增大而增大，单位时间入渗量以及本体的渗流速率也都有明显提高，极大促使基质吸力(绝对值)快速减小。

3.2 速度矢量场

速度矢量场的变化反映了雨水渗入城墙本体时，渗流速度受降雨强度、初始含水率和渗透系数等多重影响因素的变化情况。3种降雨强度下，路径Ⅰ上各节点的渗流速率随降雨入渗深度的变化规律如图7所示。

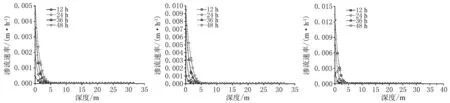
(a) 方案一(降雨强度0.05Ks) (b) 方案二(降雨强度0.1Ks) (c) 方案三(降雨强度0.2Ks)图7 不同高度处的渗流速率Fig. 7 Seepage rate with depth

从图7看出，在一定入渗深度范围内，路径Ⅰ上各节点的渗流速率变化较大；大于这一影响深度后，渗流速率降为0。

此外，任一降雨条件下，距地表一定深度范围内的渗流速率随降雨历时的增加而增大。分析原因可知，在任一降雨强度下，雨水不断入渗补充城墙本体，且表面入渗流速大于湿润锋的出渗速度，致使雨水在湿润锋上方未渗出而逐渐累积，导致表层土体接近饱和状态，造成路径Ⅰ上一定深度范围内的含水率增大，渗流速率变大。此外，对比不同方案下表层渗流速率可知，随着降雨强度的增大，城墙表层渗流速率有显著提高。这表明降雨强度在一定程度上也会决定城墙表层土体的入渗速率以及入渗量。

3.3 入渗深度

明确城墙本体受降雨入渗影响的深度范围，是计算城墙滑动面以上下滑力增大值的前提[17]。从前述结果可以看出，在任一降雨强度下，城墙本体一定深度范围内的渗流速率有较大变化，大于这一深度值后，渗流速率将变为0，此深度值即为降雨入渗的影响深度。三种降雨方案对应的入渗深度影响规律类似。将方案二所对应的降雨强度施加于城墙表面，分析饱和度在路径Ⅰ上随深度的变化情况，由此可直观看到不同降雨历时下的降雨入渗影响深度，如图8所示。

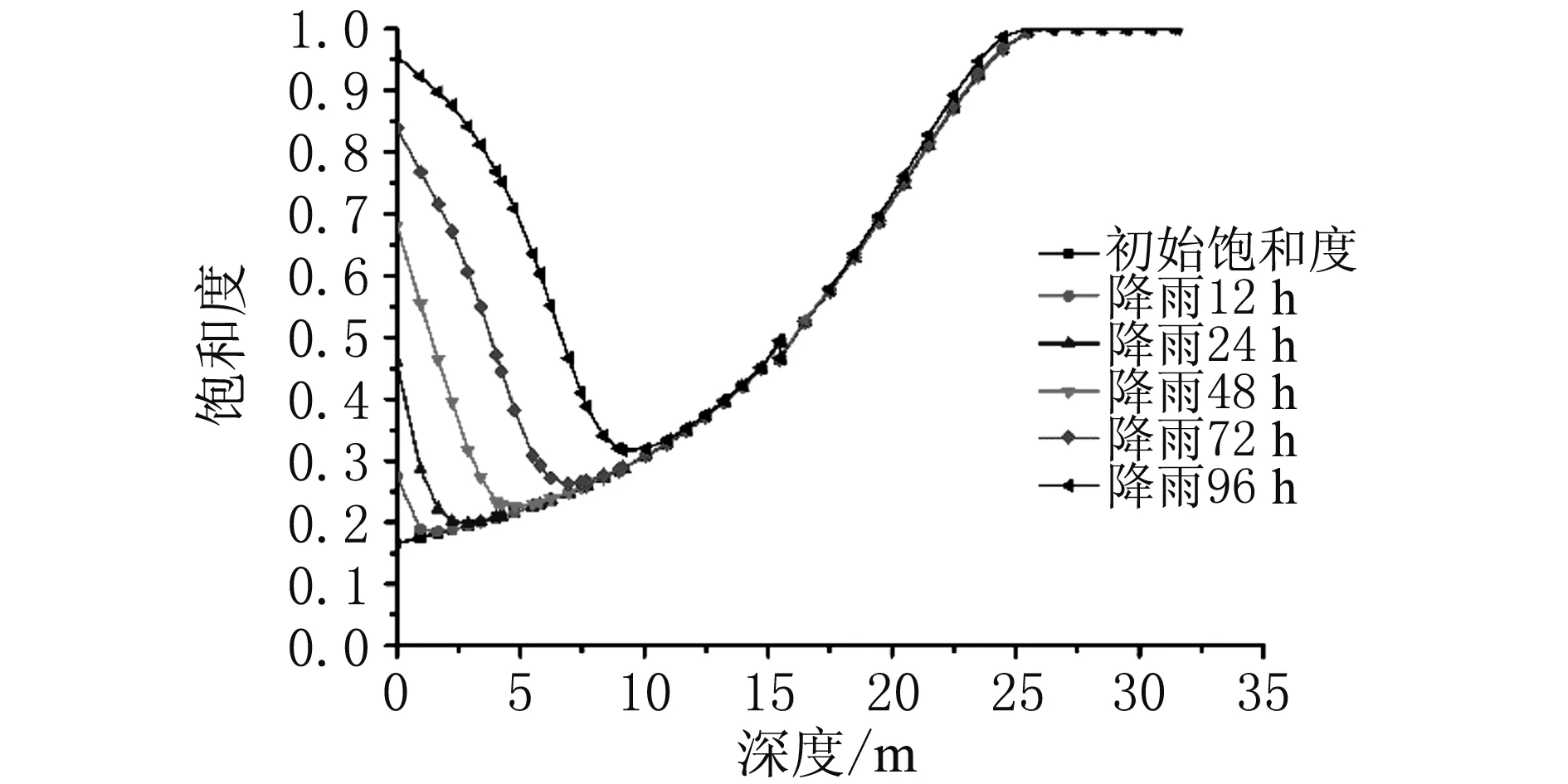
图8 饱和度随深度的变化Fig. 8 Variation of saturation with depth

由图8可知，任一时刻下，饱和度在城墙深度范围内的变化规律是相似的。受降雨入渗作用影响，表层土体的饱和度有所提高，且饱和度的增长幅度与降雨历时呈正相关关系；在表层土以下，随着深度的增加，饱和度逐渐变小。任一降雨历时下，大于影响深度的本体部分，其饱和度随深度变化的曲线与初始饱和度曲线相重合，此重合处对应的深度值即为降雨入渗的影响深度。降雨历时越长，入渗影响深度越大，超过影响深度范围的土体饱和度则不受降雨入渗影响。

降雨入渗影响深度范围内，渗流引起土体含水率增大、基质吸力减小、土体重度增大以及滑动面以上下滑力变大，这对土体强度及城墙稳定性而言是非常不利的。基于方案二的降雨强度作用下，降雨历时与降雨入渗影响深度的关系如表2所示。

表2 不同降雨历时下的入渗影响深度

3.4 坡角和平台

从图2可以看出，城墙左侧从上到下呈现不同的梯级，而阶梯状的结构(不同坡角的坡面、平台)会影响降雨入渗过程，进而影响城墙表面孔隙水压力、饱和度的变化。现选取城墙左侧特征点E、F、G，分析不同坡角对城墙本体内渗流规律的影响。表3所示为特征点E、F、G所在城墙表层土体地表与地面的夹角(以逆时针方向为正)。特征点E、F、G在降雨强度为0.2Ksm/s时，各特征点饱和度随降雨历时的变化规律如图9所示。

表3 特征点位置

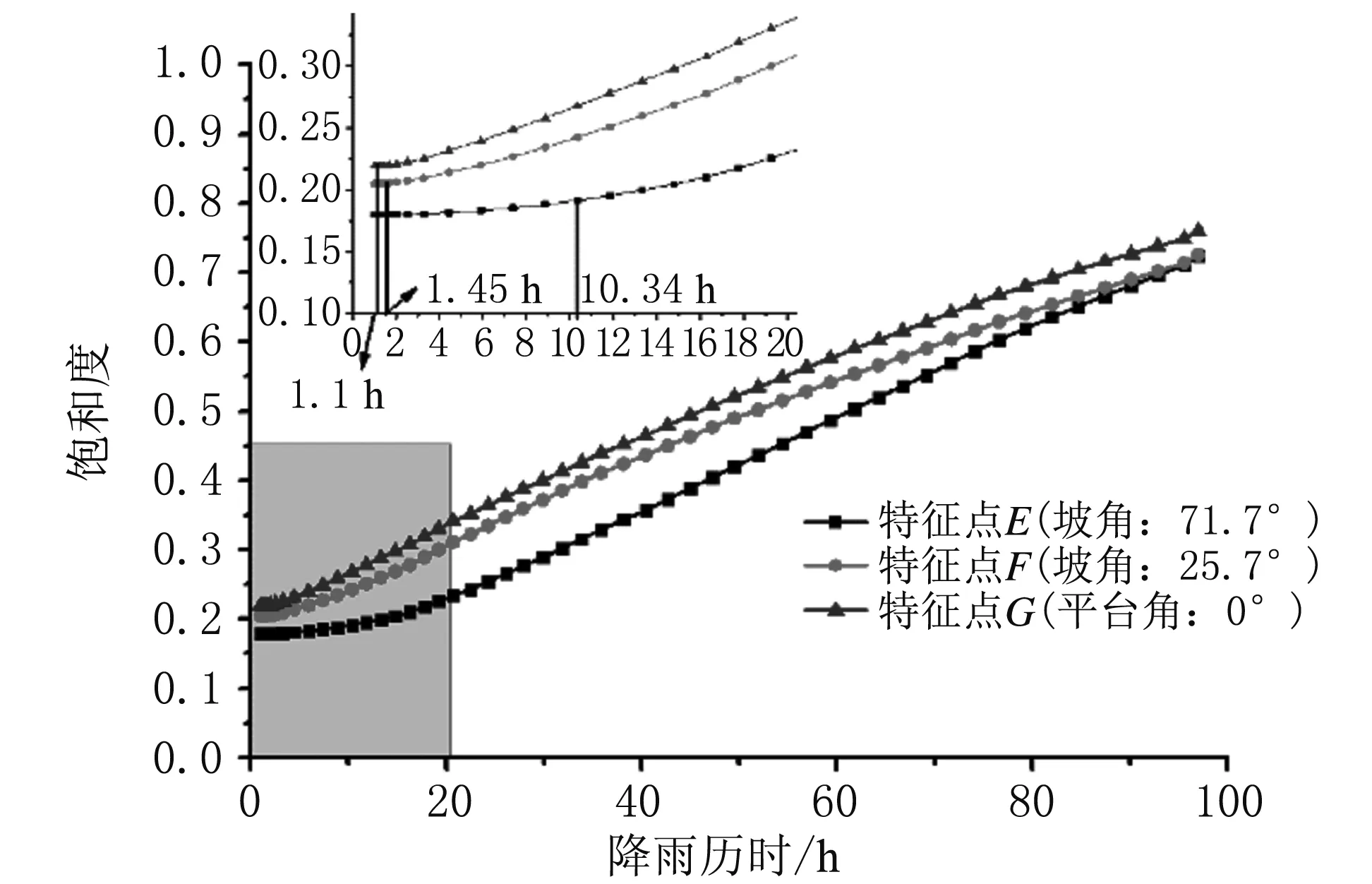
图9 饱和度随时间的变化过程Fig. 9 Variation of saturation with time

由图9可知，降雨期间，各特征点处饱和度随降雨历时的增加不断增大；特征点G(坡角0°，平台处)的饱和度始终大于特征点E、F，其中特征点E(坡角71.7°)处饱和度最小。值得注意的是，城墙左侧平台以下0.5 m 深度处的特征点G是在降雨1.1 h后饱和度开始发生变化，且增长速率较大；特征点F(坡角25.7°坡面)的饱和度是在1.48 h之后有明显增长；而特征点E在降雨10.34 h之后饱和度才出现明显的增幅，且增长速率明显小于特征点F、G。这是由于降雨期间特征点G所在的城墙平台处将汇集更多上部雨水径流，使得入渗率更大，受降雨影响的响应时间也最短；而在特征点E、F之间，随着坡角的增大，入渗率以及单位时间入渗量减小，受降雨影响的响应时间也增加。因此，饱和度以及饱和度的变化速率在城墙左侧平台处最大，随着坡角的增大而减小。此外，随着降雨历时的增加，饱和度增大，但增长速率有所减缓，且趋于相同。可见，城墙的结构特征(坡角、平台)是影响城墙降雨入渗的重要因素，尤其是降雨对城墙平台处的影响最大，平台处失稳风险更大，所以在古城墙遗址的修缮保护中，应对城墙平台处的防排水予以足够的重视。