泛Kennard-Stone算法的数据集代表性度量与分块采样策略
2022-10-14武晴滢祝震予吴剑鸣徐昕
武晴滢,祝震予,吴剑鸣,徐昕
(复旦大学化学系,上海 200438)
在大数据驱动的机器学习建模中,针对拟解决的问题,搜集或主动采集足量(或尽可能足量)的数据样本,以组成建模所需的数据集,是进行机器学习不可或缺的重要环节[1].Kennard-Stone(KS)算法(原文称之为Computer-aided design of experiments,CADEX)于1969年由Kennard和Stone[2]提出,被证明是优秀的数据集分割方法[3,4],迄今仍在广泛应用[5~8].为了满足不同应用需求,在传统KS算法基础上改进的新算法不断涌现,如用马氏距离代替欧氏距离的MDKS(Kennard-Stone algorithm based on Mahalanobis distance)[9],将因变量Y计入欧氏距离的SPXY(Sample set Partitioning based on jointX-Ydistances)[10]和考虑自变量和因变量权重的SSWD(Subset Selection based on Weightedxandyjoint Distances)[11],进 一 步 将 核 函 数 距 离 代 替 欧 氏 距 离 的KSPXY(Kernel distance-based Sample set Partitioning based on jointX-Ydistances)[12]、考虑因变量预测误差分布的SPXYE(Sample set Partitioning based on jointX-Y-Edistances)[13]、考虑特征向量间余弦距离的HSPXY(Sample subset Partition method based on joint Hybrid correlation and diversityX-Ydistances)[14],以及针对时间数据流的KSB(Kennard-Stone Balance Algorithm)[15].在上述方法中,除KSB外,其它方法可以看作为在传统KS算法的特征空间“距离”本身挖掘算法在不同应用方面的潜力.如,在欧氏距离、马氏距离和余弦距离之外,还可以引入切比雪夫距离、闵可夫斯基距离及半正矢距离等[15],以期从原有数据集中获得尽可能高代表性的子集,以适用不同的应用需求.但这些方法采出的样本集是否具有足够的代表性,由于缺乏可实际量化的标准,只能依靠最终的建模效果进行事后评价.本文从建模所需数据集的完备性入手,尝试探讨采样集的代表性,提出可定量化采样数据集代表性的一种通用性度量.此外,由于KS算法及其变种(泛KS算法)的计算复杂度为O(K3),限制了它们在大型数据集上采样的效率.为此,提升算法效率有利于提高其可用性,同时采用分块采样策略,可以显而易见地提升采样效率.
1 基本概念与条件设定
1.1 数据集的完备性
当所组建的数据集对于拟采用的机器学习模型是“足量”的,意味着它们能够以足够的密度分布于模型的所有特征空间,可以完整地反映模型所需的各种数据特征.假设问题可由J个线性无关的特征来表示,即这些特征构成J维的希尔伯特空间.若完整描述某个特征维度所需的最少数据量为N(jj=1~J),将该维度划分出Nj个空间区域,每个区域保有一个数据样本,相邻空间区域的样本尽量远离,这一数据集可称为完备集.此时,整个数据集所需的数据量至少为,同时要求每个样本必须分属不同的希尔伯特空间网格.
当每个特征维度仅有0和1两种可能(即二分法),则这个模型为最简单的模型,其完备集的样本量为2J.倘若每个特征维度都是线性的,不考虑数据本身误差的情况,其完备集的样本量最小为2J或3J(Nj=3是为了避免同一维度中两点过于接近导致数值上拟合斜率误差过大).当数据本身可能有一定误差(但误差较小的情况),且每个特征维度为线性或近似线性的,则每个特征维度通常至少需要5个点,则完备集的数量至少要5J.当问题比较复杂,其特征维度不能以线性描述,尤其是无法预知其具体的非线性函数时(这也是采用非线性神经元的神经网络模型经常遇到的情况),要完整表示这个维度的趋势,所需的样本点数量则难以估计,急剧降低了获取完备集的可能性.针对此情况,为了获取尽可能完备的数据集,首先要确定每一个维度的上下界(适用范围),然后进行必要的网格划分.原理上,网格的密度需与拟研究问题的模型梯度的变化量成正比.由于事实上大多情况下梯度变化量是预先不可知的,因此只能在建模初期,在可承受的范围尽量提高网格密度.在初步建模拟合后,根据拟合模型中各区域的梯度变化量以及拟合误差调整网格密度,实施补采样,进行再拟合,依此迭代至收敛.最终收敛得到的希尔伯特空间网格,暂且称之为精细网格,也即只要每个精细网格中保有一个数据点,所组成的数据集为该模型所需的完备集.
1.2 数据集的可代表性
当一个数据集覆盖了所有的精细网格,即其理论上拟解决问题的完备集是该数据集的子集,则可称此数据集是“足量”的.由前述可知,对于高特征维度的复杂模型,“足量”数据的获取是极其艰难的任务.在很多情况下,由于没有条件实施系统网格化数据采集(如,难以确定精细网格,或精细网格数量非常庞大,或难以按拟定的特征获取数据),只能根据实际可获得的数据进行建模.当一个数据集对于拟解决问题时“足量”,意味着该数据集包含一个完备集,同时还可能存在数据冗余,即某些精细网格区域存在不止一个数据点,甚至存在两两相同(或极其相似/近)的数据点.如果存在大量冗余数据,不仅增加了模型拟合的代价,冗余度不均也会给拟合模型带来偏差.由于拟合过程中,一般的损失函数进行误差统计时,对每个样本是同等对待的,冗余度越大的网格空间对最终模型的贡献也就越大.最终拟合模型对冗余度大的网格空间内的数据点的拟合精度要高于数据稀疏的区域.非系统性网格化数据采集获得的数据集,非“足量”却又包含大量冗余甚至重复数据是很普遍的现象.
在此种普遍情况下,从已有数据集G抽提出尽可能完备的子集G(rGr⊆G),即Gr占据G所分布的所有精细空间网格,使得Gr可以完全代表G,有利于以最小的代价建立合理的模型.假设一个数据集有K个数据点,第k点(1≤k≤K)包含了J个线性无关的特征xkj(1≤j≤J)组成的向量Xk,和对应的预期结果Yk.每个特征分别有相应的上界(Uj)和下界(Dj),即xkj∈[Dj,Uj]或xkj∈(Dj,Uj).当精细网格的分布是均匀的(或每个特征维度均为近线性,或已变换成近线性的),相邻网格之间的距离ε是恒定的.当ε已知,可以应用泊松盘采样方法[16,17],从G抽提出G(r也可应用KS采样算法,并设定采样距离r小于ε时终止采样).事实上,拟解决问题在被理解透彻之前,精细空间网格的划分不可知,因此ε也不可知.当无法确定合适的ε时,也就无法应用泊松盘采样方法获取.当ε越大时,即空间网格越大,对整个特征空间的描述就越粗线条,反之越精细.因此,可以以特征空间中距离r最远的两个数据点开始,不断逐级缩小采样距离r,同时确保所有已采样本间的距离均不小于r,来实施采样获得Gr.KS算法等效地实现了这个过程.需要注意的是,经典的KS算法不是以r的大小为终止采样的判据,而往往是以设定的拟采样数目来终止采样.当不选择r为0的情况,KS算法就排除了G中所有相同的数据点.当两个数据点距离小于ε时,这两个数据点被认为是相似或互为冗余的,设定r=ε时终止KS采样,则可以筛除G中所有r<ε的冗余数据.因此,选择所有两两之间的距离r≥ε的数据组成的Gr可以完全代表G.
2 算法与改进
2.1 经典KS算法
经典KS算法提供了从一个含等构数据的数据集G中选取预定数目样本的方法.这个数据集要求所包含的每个数据为包含n个特征的一维向量.为了确保筛选的样本子集分布均匀,对于包含K个样本的数据集G,Kennard和Stone[2]设计了以下多步操作:
(1)首先计算两两样本之间的欧氏距离dp,q,构造所有数据样本间的距离矩阵.
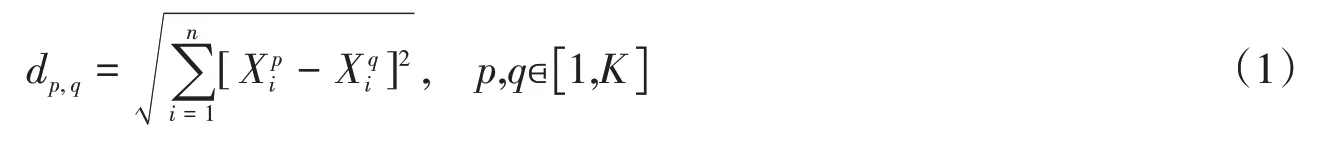
式中:Xp和Xq分别为样本p和q的特征.这部分的计算复杂度为O(K2n).
为了保证计算获得的欧氏距离在数值上的合理性,一般在进行本步骤前,需将整个数据集的每个特征分别进行归一化,以确保计算欧氏距离过程中每种特征的贡献一致.对于不同的KS变种,如SSWD[11],可以根据各特征的重要性程度统一调整不同特征的权重大小.
(2)选出其中距离最大的两个样本(k=2).
(3)对于每个剩余样本[共(K-k)个],确定其与已选k个样本之间的最短距离.

然后,选择这些最短距离中相对最长的距离rk+1=max{di,min,…,dK-k,min}所对应的样本,移入已采集的样本池.
(4)重复步骤(3),直至所采出的样本个数达到事先确定的数目为止.
步骤(2)~(4)的计算复杂度为O(K3).KS采样的结果与数据集的样本顺序无关.
除了KS算法及其各种改进版本外,还有许多方法用以从样本库中选择具有代表性的子集,如随机抽样(RS).基于能量距离最小的支持点(Support Point)的SPlit[18]、PVLOO(Posterior Variance of Leave-One-Out cross-validation)[19]、Kohonen自 组 织 映 射[20]、D-optimum[21]、OptiSim(Optimizable K-Dissimilarity Selection)[22]、IOS(Isolation forest Outlier detection and Subset selection)[23]和GDBSCAN(Generalized Density Based Spatial Clustering of Applications with Noise)[24]等.RS凭借着其简单易用性,无人为偏差,被广泛应用于样本分割.当数据集G的均匀性和冗余度很高时,通过RS采集出的GRS具备包含Gr的可能性.在数据分布均匀的情况下,冗余度越高,可能性越大.然而GRS不能保证对G的代表性,尤其存在数据密度分布不均衡(如部分重要网格区域数据点稀疏)的情况.当选出的数据集不包含部分边界上的样本,很可能导致非线性模型在边界区域产生巨大的偏差,使得适用范围受到压缩且未能提前预知.泛KS算法是除RS以外最为常用的一类采样算法,它们在机制上首先保证了数据集特征定义域边界上的样本被优先采集,已采集样本相互间尽可能远离,从而达到均匀筛选样本的目的,在诸多应用中被证明在样本分割方面具有优势[3,4,7].
2.2 采样集代表性度量
由经典KS采样算法可知,首先选择的2个距离最大的样本间的距离r2=rmax.第k个样本被选中时,其与已选择的数据集中所有k-1个数据点的最小距离为rk.按此定义,不存在r1.当rk=0,则余下的K-k个数据点均为重复的数据.因此,对于一个给定的数据集G,令为一个常数.
当上述精细网格不可知,且数据集G中不存在绝对等价的数据样本(即rK>0)时,经KS算法采出的k个样本组成的数据集Gk对于G的代表性的判定,TK提供了一个度量,令Pk=TkTK×100%,则Pk可以作为一种可定量化的度量来表示Gk对于G的代表程度.由上述可知,当rk=0时,Tk=TK,即Gk为G完备的子集,可以完整地代表G,此时Pk=100%.当Tk<TK,即rk>0时,Pk<100%.若rk>ε,此时,Gk不是G完备的子集,只能部分代表G,其代表性可用Pk来近似表示.对于给定的数据集G,当P=0和P=100%时是精确的.从中选取Gk子集,其Pk值的大小可以反映数据集代表程度的高低.尽管P不满足加和性,但对于一个给定的数据集,P的相对大小具有可比性.从定义而言,由于上述提到的“距离”并不限于欧氏距离,因此,P值不仅可以用于传统的KS算法,也同样适用于各种不同距离的泛KS算法.
为了测试P值大小的实际效果,选取简正振动采样的5400个甲烷分子结构[25]中的所有21600个碳氢键组成的数据集为例.为了方便,每个碳氢键仅用2个特征来描述,第1个特征f1为每个碳氢键键长的倒数,以原子单位表示,即a-10;第2个特征f2为该键的键环境,为考虑其它化学键对该键的影响,以其中,i=1,2,3分别为其它3个碳氢键,θi为该键分别与它们的夹角)表示.进行KS采样前,分别将两个特征归一化至0~1区间,数据分布如图1(A)所示.
在这个数据集所有21600个碳氢键中,仅有2个样本间欧氏距离为0(小于10-6),冗余度极低,同时,也表明不存在两个完全等价的甲烷分子结构.当设ε=10-6,如要求Pk=100%,则采样数至少为21599.按照KS算法,从头开始选择距离最大的点,直到最后将所有的点选出,即k=K.将rk对k作图得到图2.

Fig.1 Feature distribution(2D)maps of the methane-based C—H bond dataset
当P=10%时,KS选出61个点.如表S1(见本文支持信息)中最右列的散点图显示,这部分点均匀分布在图的各个区域,邻近的两点间距也较均匀,同时保留了图1(A)中散点的大致边界,此时,rk=0.09462.而根据RS采样,同样采出61个点,邻近的两点间距大小不均,无法看出整体边界.当P=20%时,KS选出285个点,邻近的两点间距仍较均匀,且r明显更小(rk=0.03858).而RS采出的285个点组成的图与原图[图1(A)]对比,可以看出,它着重采出原图密度较大的区域.随着采样点逐步增加,P值相应升高,上述趋势表现一致.KS采样过程的采样距离从大到小选取样本,事实上,将优先选中处于最远离中心的边界样本,在采样样本数较小的情况下,已能还原数据集的轮廓与范围,并表现出均匀的数据分布.在采样距离逐步缩小的过程,在维持均匀的数据分布的同时,逐步加大样本分布的密度.而RS采样随着采样的样本量增加,逐步反映着原数据集的密度分布,无法确保顾及数据集的边界,以及样本相对稀疏的区域.当P=50%时,KS选出2431个点所组成的图[图1(C)]很好地还原了数据集的完整边界与内部细节,此时rk=0.01041,实际采样比例仅为11.25%,显示出非常高的采样效果,相比RS以同样采样数采出的图[图1(B)],其具有更高的还原度与可识别度.从P=60%起至P=90%,rk分别为0.00754,0.00545,0.00387和0.00249.因此,对于具体采样问题,也可以根据rk的大小来判断采样是否充分.由数据集的精细网格尺寸ε可知,当rk≤ε,可以认定采样集的代表性为100%,则特别地,当数据集存在冗余数据,则冗余部分的样本在P=100%之前,不会被选取,因此,可以根据P值或rk的数值来剔除冗余度.从这个意义上,P值或rk都可用来确定所需采样数k.
2.3 KS采样算法效率的提高
尽管,与RS相比,KS采样算法可以以较小比例的采样数获取较高代表性的采样集Gk.但是,KS采样算法的计算复杂度不是线性的.它的第一个主要步骤(1),需要计算所有样本的两两间距离(不限于欧氏距离、马氏距离和其它距离),计算复杂度为O(K2n).对于一个给定的等构的数据集,特征数量n是固定的,n融入前置因子,计算复杂度为O′(K2).当数据集样本量K很大时,尤其是大数据时代的数据集往往很大,导致此步骤的计算量特别庞大.该步骤中的距离计算相互没有关联,容易分布式并行实现.而接下来的筛选过程[第二步骤:(2)~(4)],需要根据rk从大到小依次采样,而且rk的数值需要等第k-1个样本确定后才能确定,因此不能对样本量K实施并行算法,只能在每个具体样本的筛选过程中进行局部算法并行化,降低了算法的并行效率.此外,数据集样本量的大小在加剧算法计算量的同时也加大了对内存的需求.当内存不足以存放所有样本的两两距离矩阵时,算法的效率还将受磁盘读写速度的瓶颈影响而急剧降低,乃至失去可用价值.
注意到筛选过程中存在重复比较大小的过程.对于某个已选样本i,与(K-k)个剩余样本间的最短距离di,min在上一个采样(第k个)循环中已经比较过{di,1,…,di,k}中的大小.因此,在内存许可的情况下,对该距离向量进行动态维护,实际只需对上一循环的di,min与di,(k+1)进行比较,往往可以在每个循环中减少O(K)量级的求最小值的计算量,使计算复杂度由O(K3)降至O(K2).最近,在空间填充设计(Space-filling design)领域的算法中,也报道了运用动态规划避免重复比较大小的类似做法[26].结果使KS采样算法的前后两个步骤的计算复杂度均为O′(K2).
此外,对于超大样本量数据集,O′(K2)仍为难以承受的情况,可以采取分别处理的折中做法,即,将整个数据集G切分成较小的S个子集Gs(s=1,2,…,S),每个子集分别实施KS采样,再将采样后的数据集汇总.这不仅降低了计算两两距离的复杂度O′(K2)中的K,同时,也减少了后续的从最短距离中取最大值的比较过程[2.1节步骤(3)和(4)]中的K.由于实际每个子集的样本量最大值受到计算资源的限制,以及计算效率的考虑,要求K/S有限.因此,随着K增大,子集数量S必然相应增大以确保K/S有限,最终总的实际计算复杂度为

接下来,需要考虑这种分块采样策略能否保证最终采样集的代表性.由于G切分成若干个子集Gs,不同子集间的样本,其特征空间大概率存在交错.可以预见在此情况下,从一个子集Gs中采出的,与相邻特征空间的另一个子集Gs′中采出的Gsk′,存在样本间特征距离小于各子集采样时的最小rk.基于此,可按数据特征空间划分子集,或简单地将数据集G按照某一主要特征维度排序后再切分,以避免子集间的特征空间交错.但仍存在相邻子集的特征空间相互接壤,由于子集采样过程中,特征空间边界的数据点往往被优先采集,使得处于特征空间相邻的子集中采样点存在彼此距离较近的情况.在实际应用过程中,即使存在少量rk较小的数据,仅略微提高了数据冗余度,对模型建立的影响较小,甚至可以忽略.从更严格的要求上,如果在合并后的Gk集基础上再做一轮KS采样,足以排除合并导致的部分数据间存在rk较小的情况,但仍需面对合并后的Gk集进行再采样的计算消耗.另外,要对大型数据集按特征空间实施系统性切分,所需要的排序过程也是非常耗时的.因此随机划分,或直接按已有的顺序切分成多个子集,再分别进行KS采样,较为现实.
3 实验部分
为了验证以这种方式进行分块KS采样的有效性,基于文献[10,12,14]中常用的柴油近红外光谱数据集[27],采用偏最小二乘(Partial least-squares,PLS)回归方法[28]构建通过近红外光谱预测柴油质量特性的模型,用于检验对比.在该数据集中,近红外光谱采集范围为750~1550 nm,狭缝宽度为2 nm,则每个数据样本包含401个光谱特征.选择每种柴油的50%馏出温度(bp50)、15℃时的密度(d4052)和总芳烃含量质量百分比(Total)3个质量特性作为测试对象.在筛除所有空缺或不完整的数据点后,数据集的基础统计信息列于表1.

Table 1 Dataset statistics of three diesel fuel propertiesa
针对这个PLS回归实验,应用KS算法的目的是将数据集划分为校准集和预测集两个子集.通过调整校准集占总数据集的比例,来检验不同代表性的数据集的建模能力.其中校准集用于估计其潜在变量的最佳数量,来确定偏最小二乘模型的复杂度,并建立校准模型.预测集用于评估所构建校准模型的预测能力,采用拟合优度(R2)来评估模型的预测效果.
为了对比不同数据集分块方案的效果,以总数据集直接KS采样的建模结果为基准,采取按原始数据顺序划分子集和随机顺序划分子集两种模式,为了避免随机算法的偶然性,平行做A,B,C 3次随机分集.基于样本总数量为385~392之间,每个分块子集最多60个样本.
从表2可知,由于PKS为按KS算法全采样后,特征距离rk从大到小排列所加和获得的Tk值与总TK值的比,因此,PKS必定大于等于其它方式所选集的P值.此外,由于Sequential是按原特征既定顺序排列的,避免了子集间数据点的特征空间交错,因此,所得P值要大于等于随机排序后再分块(Random-A/B/C)的情况.从最终的各模型拟合优度R2可见,大小趋势也与P值基本正相关,进一步反映了P值设计的合理性.分块采样后,各拟合模型的拟合优度R2sequential和R2ramdom-A/B/C,与整体KS筛选得到的样本构造出的PLS回归模型拟合优度R2差值大致保持在0.01以内.结果表明,分块筛选的方式可以在提高筛选效率的同时,合理地采出具有合理代表性的样本集.从具象化的结果,以及PLS回归测试的结果,均能反映出P值的定量化效果.但它也存在不足,即,P值尽管在0和100%是精确的,中间数值仅对单个数据集的KS采样结果有相对意义,而不具备数学意义上的加和性.关于数据集“代表性”度量的提法,基于分类目的的算法关注其数据点在聚类区间的分布量[29],而本文更关注回归算法所需的数据集的完备性.
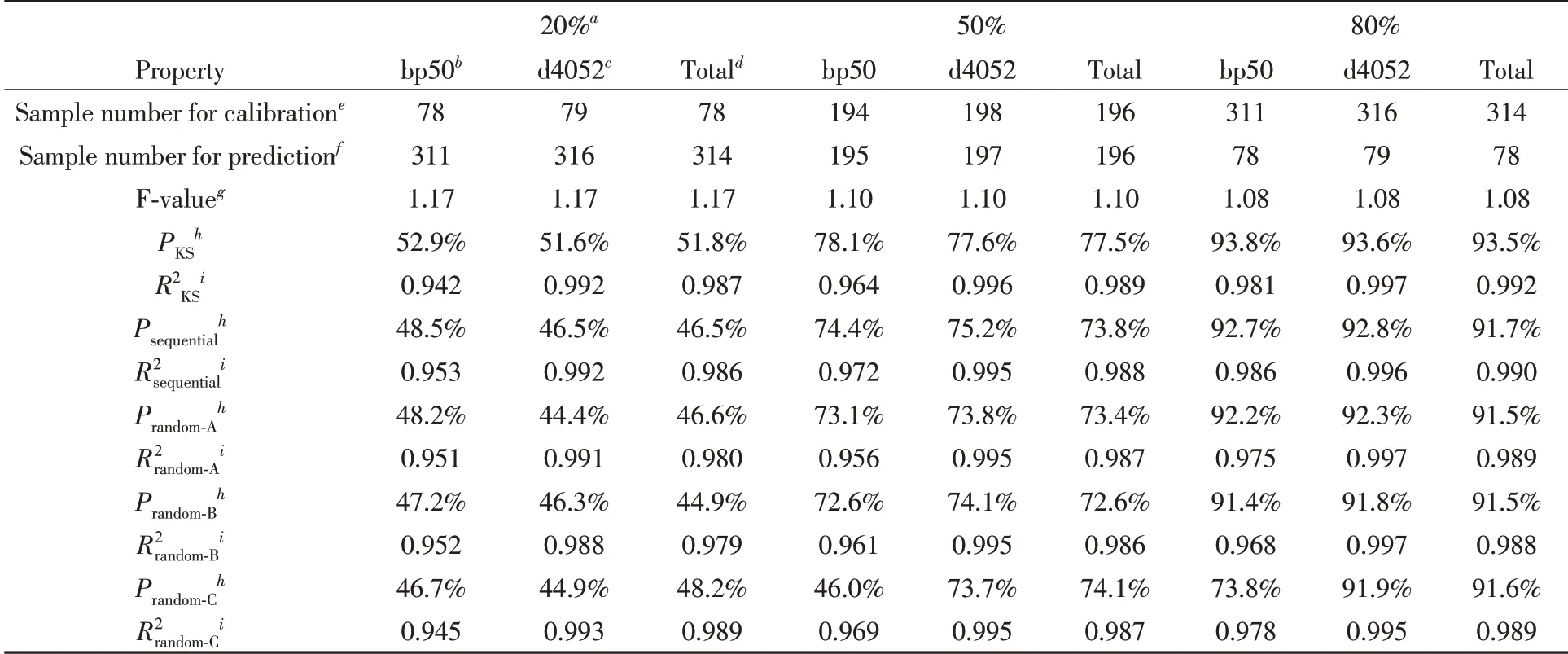
Table 2 Performance tests of different slicing KS sampling strategies
此外,由于KS类算法的计算复杂度为O(K3),与其样本总数K紧密相关,进行超大数据样本量的筛选时,其算法效率限制了其应用.针对此问题,对KS采样的筛选过程施行动态规划,可将原本的计算复杂度从O(K3)降至O′(K2);提出分块采样的解决方案,进一步将计算复杂度从O′(K2)降至O′′(K),并通过PLS回归测试,达到了预期效果,在提高筛选效率的同时,合理采出具有合理代表性的样本集.
4 结 论
在大数据驱动的机器学习建模过程中,由于特征空间维度J往往不是一个很小的数,实际数据集要覆盖所有特征空间精细网格几乎是不可能完成的任务.从实际尽可能汇集到的数据集中筛选出能够代表该数据集的训练集(或校准集),是机器学习建模成功的关键基础.传统的KS采样算法,及用各种定义的“距离”替代原有的欧氏距离的改进版本,为不同应用领域的样本筛选提供了强有力的算法基础.这些方法原理上均可以筛除数据集中的重复样本,当可以定义精细网格间距ε时,设定最小采样距离rk≥ε可以筛除冗余样本,以提高建模效率,并降低数据密度分布不均带来的偏差.由于数据集代表性迄今仍未有一个定量化的度量,无法在建模前判断采样是否充分,本文提出了以实际采出的训练集(或校准集)中每个样本的采样距离的和(或积分值)Tk与所有样本的TK的比值P,来定量化表示泛KS算法抽提出的训练集所能代表总数据集的程度.针对KS复杂度问题,对KS采样的筛选过程施行动态规划,并提出分块采样的解决方案,将计算复杂度从O(K3)降至O′′(K),在提高筛选效率的同时,采出具有合理代表性的样本集.同时,事先对数据集中至少一个特征维度进行排序再分集,可有效避免各子集的特征空间交错导致采样效果(汇总后的训练集的均衡度)降低.特别当数据集中样本分布极度不均衡的情况下,如大部分特征空间区域样本稀疏,而极小部分特征空间存在大量冗余样本时,预先按关键特征维度排序后再分集采样,有助于保障分块采样策略的效果.如有必要,在计算资源许可的情况下(汇总的采样集样本数K不太大),对汇总的采样集再实行一次KS采样,可以获得严格的采样集.
支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20220397.
