精细龙格库塔法计算变压器绕组的过电压分布

2022-10-14田丰源赵新贺王秋富

中国测试 2022年9期

张萍，田丰源，赵新贺，王秋富

(1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学），天津 300130;2. 河北工业大学人工智能与数据科学学院，天津 300130)

0 引言

气体绝缘变电站(gas insulated substation)中隔离开关分合闸操作时会产生上升时间，为纳秒级，暂态频率高达兆赫兹的特快速暂态过电压(very fast transient over-voltage，VFTO)[1-2]。当VFTO侵入大型电力变压器等电气设备时，极易破坏电气设备的绝缘，给电力系统造成严重的经济损失。受现场环境的制约，目前直接开展VFTO下大型电力变压器绕组的绝缘实验条件要求很高，所以仿真分析VFTO作用下的变压器绕组过电压分布具有重要的理论意义和工程价值[3-4]。

目前针对变压器绕组建模分为3种：集中参数模型、集中-分布参数混合模型、分布参数模型。集中参数模型是把变压器线圈划分为若干单元，把每单元用集中电感、电容、电阻来表示，它的适用频率范围比较窄，适应于低频和中频情况下的建模[5]。集中-分布参数混合模型是把变压器绕组分为两部分，对其重点研究的部分采用分布参数模型进行建模，对其他线饼采用集中参数模型进行建模，这样虽然避免了大量的计算，但变压器绕组中的电磁场是紧密耦合的，此方法破坏了电磁场的连续性，结果容易产生偏差[6]。分布参数模型是以变压器线匝为单元，每一匝看成一根传输线，根据线匝的电气连接顺序，求得变压器绕组上电压与时间和空间的关系。当需要考虑参数的频变效应时，可以在频域中计算电压的响应。这种模型更加准确，并且适应于高频情况，更能反映出VFTO作用下变压器绕组内过电压分布的规律[7]。

文献[8]对变压器的多导体传输线方程离散成微分方程组以后，使用精细积分法求解，但这种方法涉及到大量的矩阵运算，会造成误差过大、计算效率过低。针对此不足，在前人基于分布参数模型对变压器绕组建模的基础上，提出了精细龙格库塔法计算电力变压器绕组过电压分布，采用矢量匹配法和递归卷积处理频变参数的方法。该方法在非线性动力学与结构力学方面得到了广泛应用，该文将其应用到变压器绕组过电压求解领域。通过仿真结果和实际测量结果相比较，精细龙格库塔法相比较于精细积分法，误差更小，计算效率更高。

1 精细龙格库塔法

1.1 多导体传输线模型

对连续式变压器而言，将变压器绕组在每匝换位处打开，不考虑传输线的频变效应，变压器绕组就等效为线匝长度均为l且每根互相耦合首尾相连的多导体传输线模型，如图1所示[9]。

图1 多导体传输线模型

模型的时域形式为：

式中：u和i——距离始端x处的电压、电流向量；

R、L、G、C——单位长度传输线的电阻、电感、电导、电容矩阵。

1.2 多导体传输线模型的空间离散

变压器绕组的多导体传输线模型的电报方程是偏微分方程组，采用欧拉公式对传输线的电报方程进行空间离散。

为了介绍方便，以变压器绕组的单导体为例进行说明。图2中传输线长度为l，把它按照空间距离分为M段，那么每一段长为Δx=l/M。

图2 传输线的分段

假设传输线的首端接电阻为RS，末端接电阻为RL，边界条件为：

假如传输线的分段数为M，把分段处的电压和电流看作自变量，此时有2M+2个自变量，结合边界条件式(2)整理得要求解的变量为2M个。

运用欧拉公式对式(1)进行空间离散，其中式(1)的第二式在(k+1)h处离散，第一式在kh处离散得：

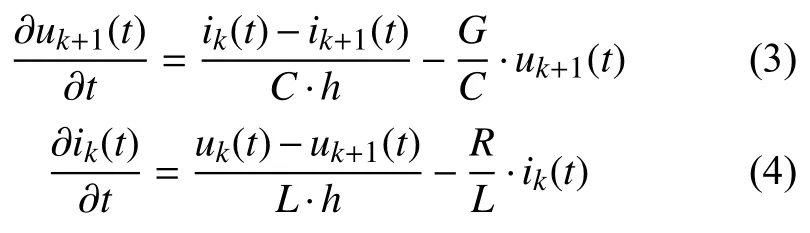
其中h为空间的步长，k=0,1,2, ···,M。

式(3)变换得：

其中u1,u2,···,uM是状态变量。

式(4)变换得：

其中i0,i1,i2,···,iM-1是状态变量。

经欧拉公式离散后的传输线方程包含了2M个独立的状态变量，根据式(2)将u0用i0线性表示，iM用uM线性表示，得线性常态状态方程组：

其中F为常数矩阵。

对于多导体传输线模型，就是将具有N匝的变压器线圈用N根频变的耦合传输线进行建模，每根传输线分为M段，可得公式(7)，相应的参数将变为矩阵和向量。

1.3 精细积分法

精细积分法是常用的求解微分方程方法，该方法适用于齐次和非齐次常微分方程的求解[10]。该文将使用精细积分法求解式(7)，得到变压器绕组在VFTO作用下的过电压分布。

由常微分方程组的理论可以知道，式(7)的解可以写为：

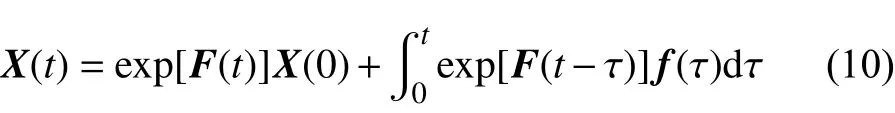
时间步长设为δ，一系列等长δ的时刻为：tj=jδ,j=0,1,2,···，当t=jδ，有：

经过推导，在tj≤t≤tj+1的任意时刻，有：

当t=tj+1=(j+1)δ时，有：

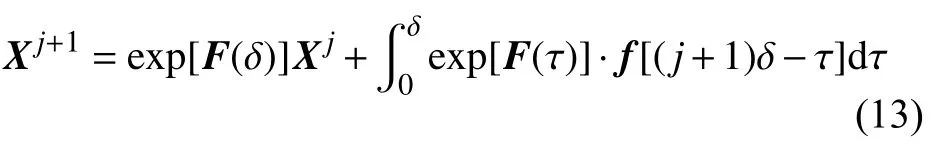
式(13)为精细积分法求解VFTO作用下的过电压公式，但单纯采用精细积分法会涉及到大量的矩阵运算，造成计算量过大，而且还带来较大的计算误差。所以在求得式(13)以后，使用龙格-库塔法求解式(13)等号右边的积分项，这样就避免了大量的矩阵运算，使误差减少，计算速率更高。

1.4 龙格-库塔法

龙格-库塔法是一种求解常微分方程的高精度算法，其中4阶龙格-库塔迭代法因精度高、稳定区域广、编程简单被经常采用[11]。本文采用4阶龙格-库塔迭代法求解式(13)等号右边的积分项，得到VFTO作用下大型电力变压器绕组过电压与时间和空间的关系表达式，如下式所示：

式中：k1,k2,k3,k4——4阶龙格-库塔方法的系数；

δ——时间步长。

2 频变参数的处理

变压器绕组的分布参数在频率较高的情况下，会出现明显的频变，该文用矢量匹配法和递归卷积处理频变参数[12]。以集肤效应为例说明。

高频集肤效应时，单位长度电阻为：

式(1)的第一式可写为：

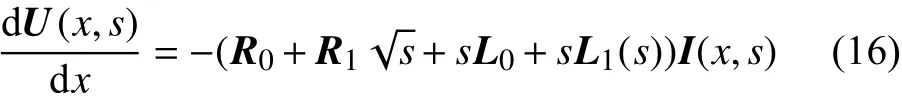
式中：ki——第i个极点；

pi——第i个留数。

代入式(16)得：

式中：n和m——和L(s)匹配的阶数；

k——极点；

p——留数。

将式(17)进行拉氏反变换得：

其中λ1和λ2为卷积项：

采用同样的方法，对式(1)的第二式进行相应处理。

对任意空间点x，式(19)做以下变换：

设时间步长为τ，在时刻n有以下递推关系：

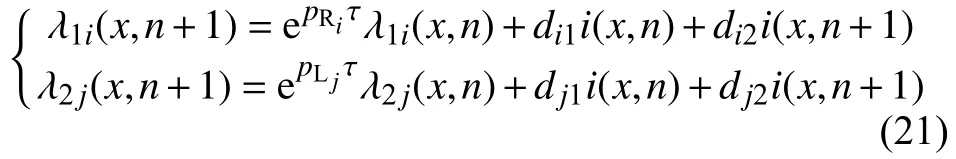
其中：

式(21)等号右边可以进行同类项合并，整理可得标准的状态方程。

3 方法验证和算例分析

首先对文献[13]中的变压器模型进行仿真，与实测结果进行对比，验证了所提方法的准确性，并仿真了本课题组的一台由18饼，每饼10匝构成的连续式变压器模型。

3.1 方法验证

文献[13]中变压器的结构参数如表1所示。

表1 变压器结构的基本参数

使用该文的方法，可得：

式（22）可化简为：

其中=R1+L1。

频率范围选取的是1～107Hz，采用对数平均分布104个频点，矢量匹配的阶数为10阶，递推7次，匹配前后均方差为 9 ×10-3，图3为矢量匹配的幅频特性曲线图。

图3 矢量匹配的幅频特性曲线

图4为文献[13]中所施加在变压器绕组上的电压源，图5～图7为精细龙格库塔法与精细积分法仿真的第100、200、400匝末端过电压。

图4 电压源

图5 第100匝末端过电压

图7 第400匝末端过电压

比较使用本文方法仿真的第100匝、200匝、400匝的结果和文献[13]的实测结果，发现实测结果和仿真结果基本相一致，证明了本文算法的准确性。

图6 第200匝末端过电压

表2为实测与仿真输出电压峰值对比，由精细龙格库塔法计算出来的第100匝与实测值的误差为1.2%，第200匝的误差为1.3%，第400匝的误差为2.1%，而使用精细积分法计算出来的第100匝、200匝、400匝的误差分别为3.8%、4.8%、3.7%，通过对比分析可知，使用精细龙格库塔法的误差均小于精细积分法的误差。所以精细龙格库塔法在计算变压器绕组过电压分布比精细积分法更加有优越性。表3为在同等条件（CPU2.2 GHz，4 GB内存）下两种方法耗时比较，使用精细龙格库塔法计算时间为325 s，精细积分法计算时间为653 s，经计算，精细龙格库塔法比精细积分法减少50.2%的计算时间。

表2 测量和计算峰值对比

表3 方法耗时比较

3.2 算例分析

采用精细龙格库塔法对本课题组的一台变压器模型进行仿真分析，变压器模型如图8所示。此变压器线圈为连续式绕组，共18饼，每饼有10匝，变压器绕组的俯视图如图9所示，基本参数如表4所示。

图8 变压器绕组模型

图9 变压器绕组俯视图

表4 变压器模型的基本参数

采用有限元方法求得该变压器模型的匝对铁芯的电容Cg=35 pF、匝间电容Ct=144 pF、饼间电容Cs=15 pF[14]。变压器绕组过电压仿真结果如图10所示。

图10中(a)为对变压器绕组施加的上升沿20 ns、幅值为500 V的VFTO电压源，图(b)～图(f)为变压器绕组第10、20、35、50、70匝末端的过电压分布图。

由图10可知，最大的匝间过电压出现在靠近变压器绕组首端的线圈，例如第10匝线圈约为电压源最大幅值的60.2%。假如大型电力变压器长时间工作在电压幅值过高的情况下，对变压器的正常运转是极其不利的，很容易造成线圈的击穿，发生严重的事故。在生产设计变压器结构时，应着重考虑变压器首端的绝缘措施，防止事故的发生。且由图10可知，变压器绕组过电压的上升陡度在靠近绕组首端的线圈过大，之后随着匝数的增加，逐渐变缓。例如第10匝过电压峰值时间为44.12 ns，第35匝的峰值时间为84.72 ns。如此陡的过电压长时间侵入变压器绕组中，会造成绕组的绝缘老化，且其中含有的高频分量可能会造成谐振现象的发生。