基于神经网络的电力系统二次设备监测方法研究
2022-10-14史新新
史新新
(国电南瑞科技股份有限公司)
0 引言
二次设备作为智能电力系统的重要组成部分,承担着对电力系统一次设备进行监测、控制、保护的任务,与电力系统中的电能并不发生直接关联关系[1-2]。二次侧设备主要包括电压表、电流表、功率表等,主要负责采集一次侧设备的运行数据,由此判断智能电力系统的运行状态[3-4]。二次设备数量的大幅度增加,对一次设备监测的准确性造成一定程度的影响。本文基于神经网络模型对二次侧设备采集到的运行数据进行分析,通过调整权值和阈值,有效剔除冗余数据,实现监测精度的提高,并且能够对电力系统出现的异常情况进行快速的诊断,由智能电力系统做出相应的动作,保证电力系统的安全、可靠、稳定运行[5]。
1 二次设备数学分析
1.1 监测设备相关参数分析
监测设备相关参数包括电压参数θ1、电流参数θ2、功率参数θ3、温度参数θ4等,由于上述监测设备相关的参数单位是完全不同的,因此需要进行统一的标准化处理[6-7],具体的处理方法为:
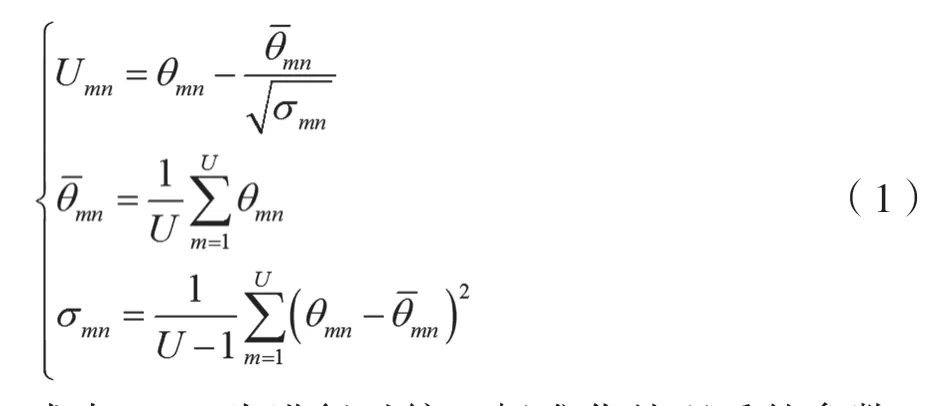
式中,Umn为进行过统一标准化处理后的参数;θmn为电流、电压等相关参数;为θmn的平均值;σmn为θmn的方差值;U为参数的数量。
1.2 监测数据优化方法
为了对监测数据进行更有效的优化,需要对数据进行聚类处理,实现数据量的简化。不同类型数据通过调整其欧式距离参数来调整聚类的具体标准[8]。本文在此基础上进行优化,提出轮廓系数的概念,基于K-means方法,设定聚类中心,实现监测数据的聚类处理,并对不同类型数据的聚类等级SE进行合理划分,完成监测数据的优化[9],其中聚类中心诊断公式为:
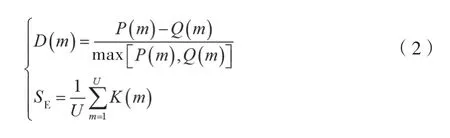
式中,m为研究对象样本中的个体;Q(m)为样本个体在整个聚类中的最大距离,K(m)为样本个体在本体聚类带其他聚类的最小距离[10]。不同类型数据所对应的聚类在全部数据中的聚类等级计算公式为:
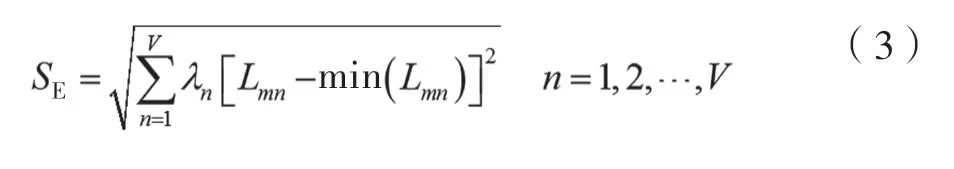
式中,λn为权重参数,全部的权重参数之和为l;Lmn为不同类型数据的聚类样本;min(Lmn)为聚类样本的中心;SE为全部的聚类中心到最小聚类中心的距离,离得越近,重要性等级越高。最后根据SE的大小排列,实现聚类数量的确定。
2 神经网络模型
2.1 神经网络
BP神经网络中,信息从输入层导入,逐级传输到输出层,输出层上生成的误差再反向传输到输入层[11]。BP神经网络的结构如下图所示。
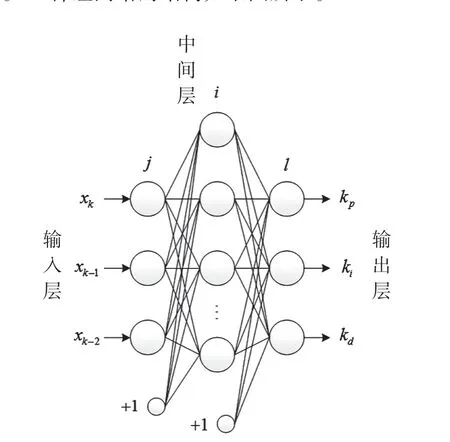
图 BP神经网络拓扑结构
节点采用Sigmoid函数来描述,即:
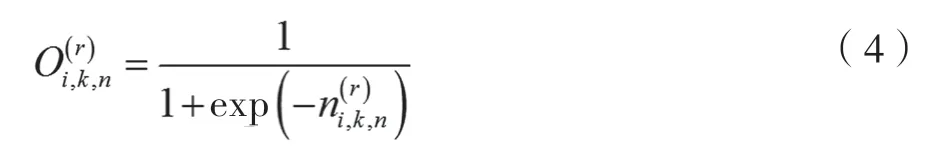
2.2 模型数据运算
二次设备经过神经网络模型的输入层,进入到中间层处理,最终从输出层导出,在数据进行反向传输时,中间层会根据阈值和权值参数对数据进行判断,对于不符合要求的数据则剔除掉。将二次侧设备研究对象样本描述为RU=(R1,…,Rv),中间层数据描述为SU=(S1,…,Sw),输出层数据描述为TU=(T1,…,Tl),输出结果诊断向量为DU=(D1,…,DL);输入层与中间层之间的权重参数为λmn=(m=1,…,v;n=1,…,w),阈值参数为βmn=(m=1,…,v;n=1,…,w);中间层与输出层之间的权重参数为λnl=(n=1,…,w;l=1,…,h),阈值参数为βnl=(n=1,…,w;l=1,…,h)。由此便可以得到神经网络的正向传递公式为:
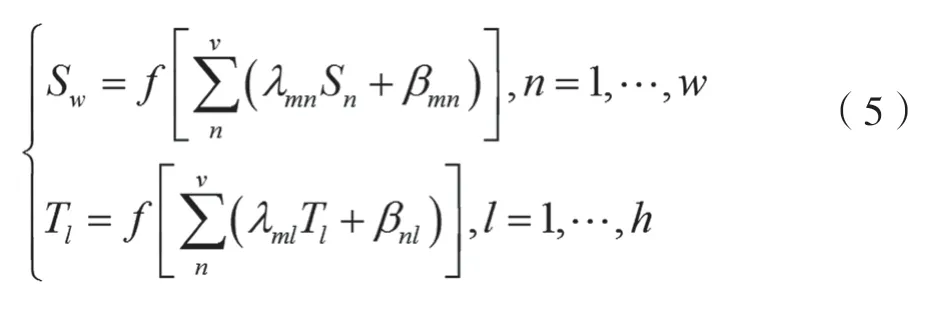
再根据输出结果诊断标准得到输出误差,及输出结果与理论结果之间的差异:
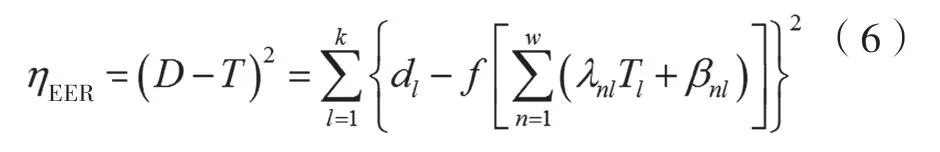
2.3 阈值分析
神经网络运算的目的就是要实现输出结果与理论结果之间的误差最小化,因此需要通过泰勒展开公式e[ε(n+1)]对神经网络模型中的阈值参数和权值参数进行优化,运算公式为:
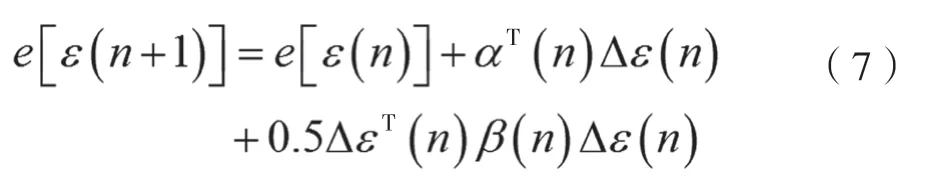
式中,α(n)为误差在梯度方向上的分量;β(n)为海森矩阵,假设存在△ε(n)=-β(n)-1α(n),就会得到误差的最小值,海森矩阵的复杂程度直接对运算速度造成影响,如果存在雅可比矩阵β=JTJ且α=JTe,则泰勒展开公式就能够简化为:
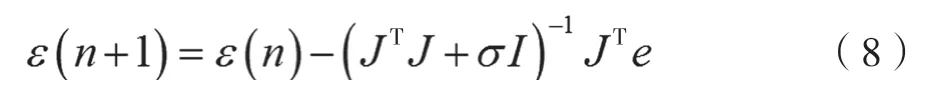
2.4 归一化运算
为了将数据的其他属性对样本的影响程度降到最低,将数据样本进行归一化处理,统一变换到 (0,1)区间内,其变换公式为:
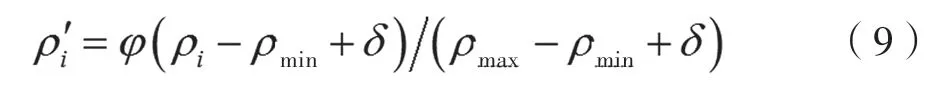
式中,ρi为样本中的任意数据;λ为归一化运算后的结果;ρmax为样本中数值最大的数据且无限趋近于1;ρmin为样本中数值最大的数据且无限趋近于0。
2.5 误差分析
二次设备的监测误差可以划分为两种,即相对误差ηX和方差ηF:

这两个误差参数能够分别反映出进行优化后的数据情况和实际的数据情况,并且通过对这两个误差参数的合理运用到阈值参数和权值参数的调节,误差分析能够更有效、更准确地对数据进行科学的分析,有效地判断二次设备数据监测的效果。
3 实例分析
3.1 监测样本描述
以某地区的电压表和电流表为例,分析神经网络算法对二次设备监测的优化效果。神经网络的输入为电压、电流、电功率、温度,对上述数据进行监测,得到聚类轮廓,如表1所示。
通过对表1中数据进行分析发现,存在不同输入变量的聚类系数和聚类分类数,当聚类等级值为5的时候,整个聚类的聚类系数最大。以此为基础展开相关分析,确定聚类中心和聚类样本,具体数据如表2所示。
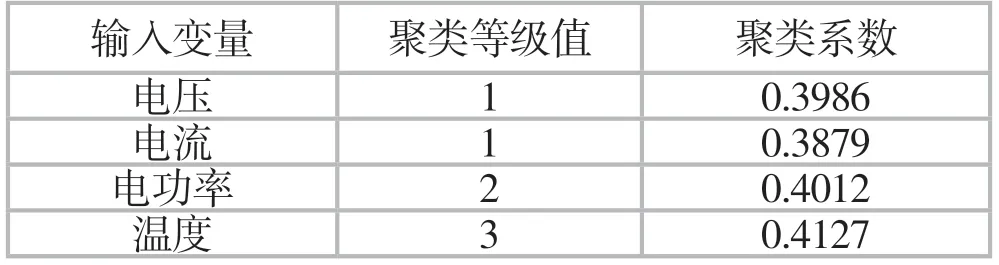
表1 聚类轮廓参数表
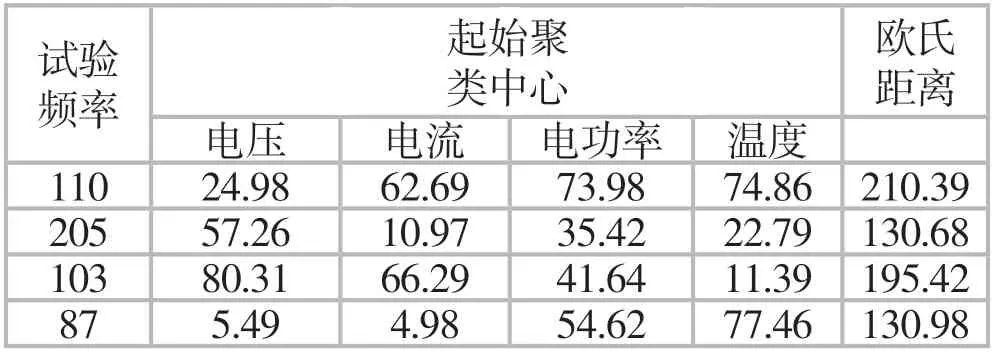
表2 聚类中心和聚类样本数据表
分析数据发现试验频率为110时,聚类效果最佳,后续功能测试都基于110进行。
3.2 二次设备监测精准度
分别在0.1、0.01、0.001三种精度要求下,对各个数值的精准度进行计算,得到的计算结果如表3所示。
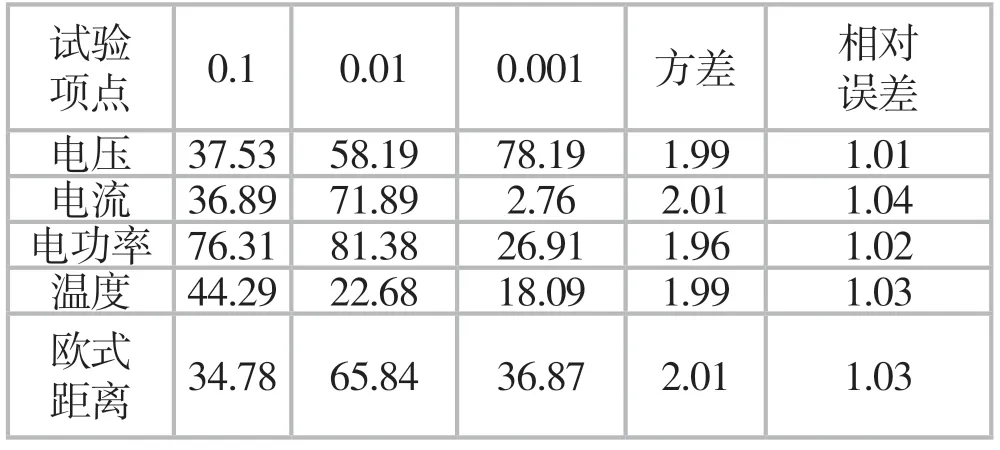
表3 不同精度要求下的误差数据表
由表3数据可知,在不同的精度要求下,计算得到的方差和相对误差都能够控制在合理的区间内,没有明显差别。
3.3 二次设备的运算时间
对二次设备的运算效率的研究,要基于不同的迭代次数展开,具体的运算数据如表4所示。
通过对表4数据进行分析可知,在迭代次数为1~100下,计算时间最长不会超过46s,运算数量最大为162。总体上来看,神经网络方法对二次设备监测的优化效果比较好,能在较短的时间内对多个样本数据进行监测,迭代次数为1~100下能够将运算精度保持在98%左右。
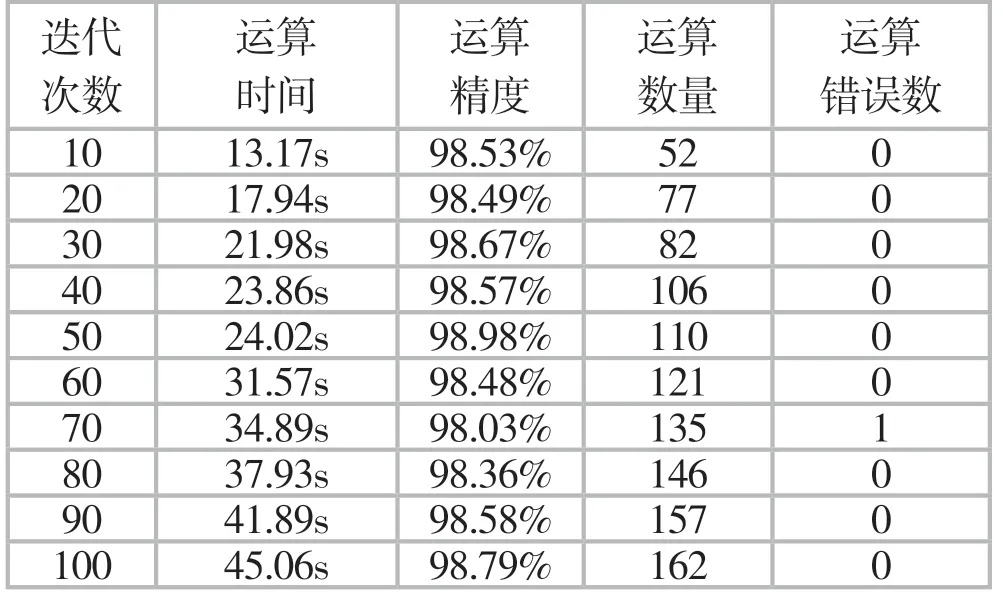
表4 二次设备运算时间数据表
4 结束语
本文将神经网络算法应用到电力系统二次设备监测优化中,通过对电力系统中电压、电流、电功率、温度等数据的监测,对理论监测数据与实际监测数据之间的误差进行深入分析与研究,测试结果表明,在不同的精度要求下,计算得到的方差能够控制在2.0左右,相对误差能够控制在1%左右;并且在进行运算时,迭代次数为1~100的情况下,运算时间最长不超过46s,运算精度能够控制在98%左右,运算数据能够达到162个。
经过本文的深入分析可知,采用神经网络方法对电力系统中二次设备监测数据进行优化,通过确定样本数据中心,配置合理的阈值参数和权值参数等有效方法,对输入到神经网络中的数据进行反复的迭代运算,最终得到符合实际情况的数据。由此能够达到二次设备对电力系统进行高效率监测的目的。
