基于高级程序设计语言的高职数学课程可视化教学探索*
2022-10-12段敏
段 敏
(湖南交通职业技术学院,湖南 长沙 410132)
1 引言
公共数学课程作为高职院校理工科专业必修的基础课程,教学的核心目标之一就是培养和发展学生的数学分析思维和工程问题建模能力[1]。然而,由于理论知识具有高度抽象性,现有大学数学课程教学普遍偏重计算能力的培养而忽视学生数学分析思维的培养。在这种教学模式下培养出来的学生往往不知道如何将实际问题转化成数学模型问题加以分析和解决,缺乏运用数学知识进行分析的思维,在解决复杂的实际问题时数学建模能力不足。
随着计算机软件技术的飞速发展,数学课程教学也逐渐引入计算机进行辅助,并针对其进行了大规模的教学改革实验。数学实验课在1988年最早由美国雷斯勒技术学院开展实施。我国对数学实验课的探索始于1997年,国防科技大学首次在课堂上开展了数学实验教学,由此开始了数学教学改革。依托该项目,李尚志教授编写了教材《数学实验》[2]。在这之后,众多高校开始关注数学课堂改革。然而,在现阶段高职院校普遍缺少数学实验课程的现状下,如何将具有大量抽象理论的大学数学课程内容生动化、简单化,调动学生学习兴趣与积极性,成为了数学公共课程教学改革面临的难题[3]。
本文提出把《高等数学》《复变函数》等高职院校公共数学课程教学过程和MATLAB、Python等高级语言程序设计软件结合起来,借助数学建模工具强大的数值计算、分析与图像处理功能,显化实际问题的分析过程和解决过程,实现数学抽象理论的可视化教学,帮助学生提高数学分析思维,提高教学效果,培养学生解决复杂实际问题的能力。
2 MATLAB、Python概述
MATLAB由美国MathWorks公司开发维护,至今已有近40年的发展,其在矩阵计算和算法开发方面功能强大,而且能够为用户提供高级可视化工具[4]。作为一款数值计算软件,MATLAB因其众多优点备受师生推崇,在数学建模、矩阵计算方面尤其受到人们的喜爱。MATLAB内含大量函数库,可随时调用,不需要大量且繁琐的编程过程。与其他编程软件相比较而言,对数学语言的亲和性更显得其编程语言的简洁优雅[5]。
Python软件最早是由来自荷兰的Gudio van Rossum于1989年创建开发的,由于该软件具有良好的交互性,又是开源语言,拓展性能好,近年来热度越发高涨,深受用户欢迎[6]。Python是一种功能性强、语法简单,在数学、物理、人工智能等各个领域都有广泛应用的编程语言。其中,Sympy库是用来进行科学计算的核心,它能够基于符号计算体系高效完成多项式计算。Sympy库能够实现多种复杂计算,具有操作简单、应用性强的特点,常被用来求解方程,尤其在计算涉及复杂数学建模问题的微分方程时常常成为首选。
3 数学课程可视化教学意义
3.1 编程成为理工科学生的必备技能
计算机技术的发展日新月异。近年来,大数据技术被广泛运用于各行业领域,熟练掌握一门编程语言已经成为从事数据分析、数据挖掘、大数据分析、人工智能等岗位工作的标配。社会对学生编程能力的要求日益提高,逐渐从加分项演变成必修项。因此,在大学阶段很有必要对学生进行编程教育。
从教学的角度来看,教师要考虑学习效果和实际应用效果,通过建模、仿真及可视化等一系列流程,能够使学生深入思考数学原理,亲自动手开展实践以解决问题,一举两得。从学生的角度来看,学生对编程语言的掌握并非一朝一夕可以实现,在熟悉数学知识的基础上开展编程的基础学习,对专业知识、编程知识体系的构建都很有好处,能够锻炼学生的思考能力和实践能力。
3.2 可视化教学改善理论教学枯燥性
教学效果因教师和学生而异。很多情况下,教师难以兼顾所有的学生,特别是在学生就业选择各不相同的背景下,教师对课程深度和知识难度的把控很大程度上会直接影响学生的学习积极性。
通过MATLAB、Python等高级程序设计语言的图像功能演示复杂函数理论与图形,能够使学生克服学习抽象理论的畏难心理,有利于学生理解和对比。教师从可视化图形入手,由简单知识过渡到数学原理,将理论知识以严谨但不失有趣的方式展现出来,能够极大程度焕发学生的自主学习热情,同时兼顾学生的基础差异,改善了数学课程理论教学的枯燥性。
3.3 可视化教学提升数学建模能力
大学数学课程有3个显著特性:抽象性较高、使用性广泛、逻辑性严密。在课堂教学中教师往往只注重讲解理论知识,忽略与实际应用相结合,使得学生无法获取更多的感性认识,从而在理论的深度与应用的广度上不能很好地结合。课堂教学不够生动形象,导致学生解决实际问题的能力较弱。
数学课程教学以数学理论知识为主干内容,以建模工具的实例化演示为辅助,一方面通过数学专业软件实现复杂函数可视化教学,另一方面通过数学建模软件的使用培养学生的建模意识和编程能力。数学建模是实际问题的理想化,是联系实际问题和数学语言的媒介。推动数学教学改革能够间接提升学生数学建模能力,辅助学生向专业领域发展。
4 数学课程可视化教学典型案例
4.1 高等数学可视化实例
以函数y=sin(1/x)、y=x*sin(1/x)的极限为例,对初学者来说求解这两个函数的极限是比较抽象的。这两个函数分别涉及到无穷大和无穷小及有界函数极限的知识,在常规教学实践中很难用语言或者板书解释清楚。通过python的可视化展示,学生可以清晰地了解该函数的分布情况,对理解极限的概念很有帮助。
Python程序如下:

结果见图1。x趋向于0时,函数值是在-1和1之间来回震荡,越靠近0频率越高,但是不会趋近于0,因为是一直在越来越快地振荡,永不停止,极限不存在。x趋向于无穷,1/x趋向于0,sin(1/x)趋向于0,函数极限为0。
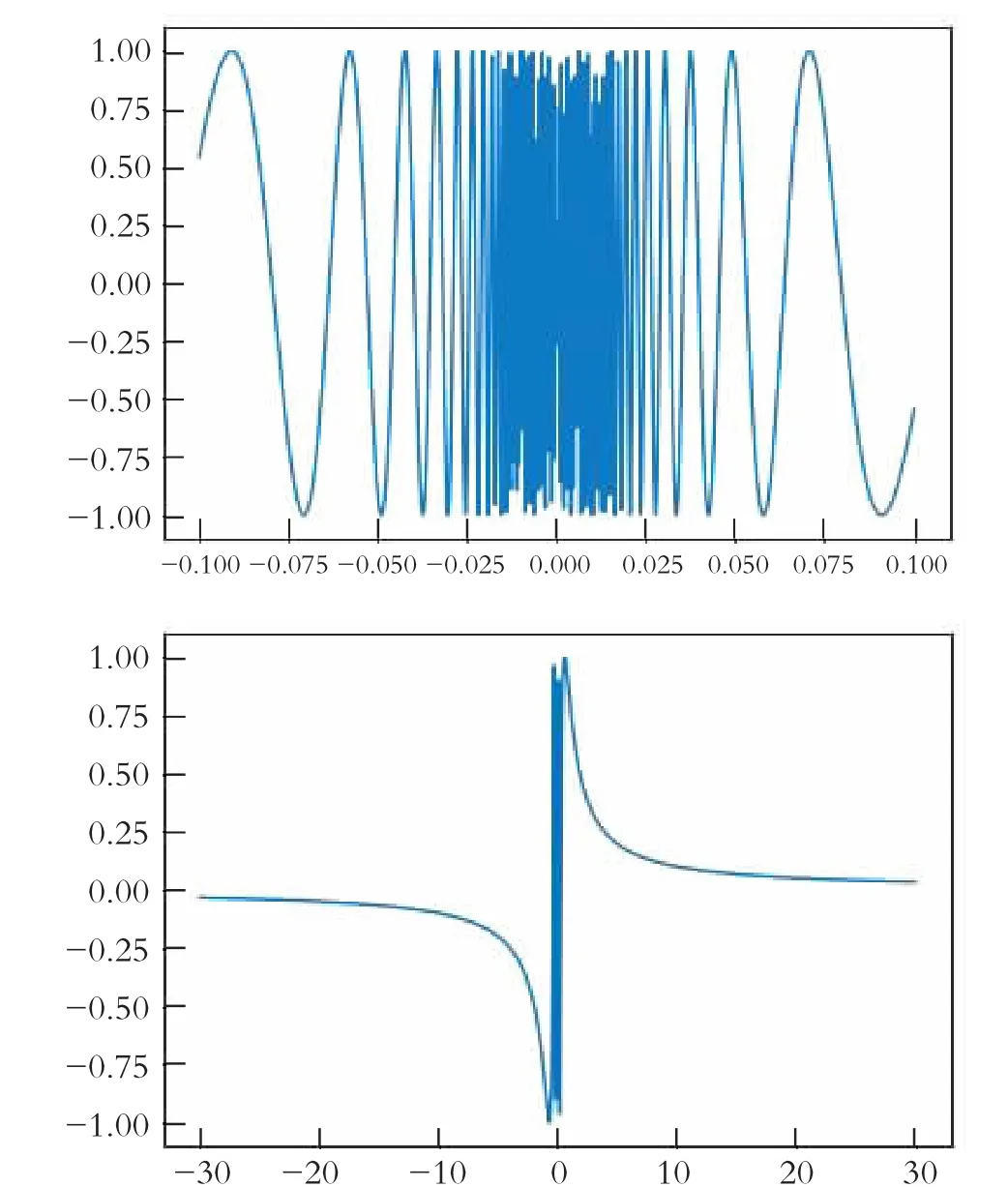
图1 函数y=sin(1/x)的图形
结果见第21图2。x趋向于0时,f(x)在0上下震荡并逐渐趋于0,极限为0。x趋向于无穷时,1/x趋向于0,f(x)趋向于1。

图2 函数y=x*sin(1/x)的图形
4.2 复变函数可视化实例
复变函数部分的内容较为晦涩难懂,其自变量和函数值中均包含复数,在图形绘制方面难度很大,特别是要在三维空间中对上述4个实、复数进行表示,更凸显了人们思维的局限性。在处理这部分时,MATLAB用颜色深度来处理第四维数据的变化,即采用3维+1维的形式具象化复变函数,xoy面表示自变量复平面,z轴表示复变函数的实部,颜色深度代表其虚部。
例:利用MATLAB作出复变函数f(z)=z5+z2+1的图像。
MATLAB程序如下:

结果见图3。
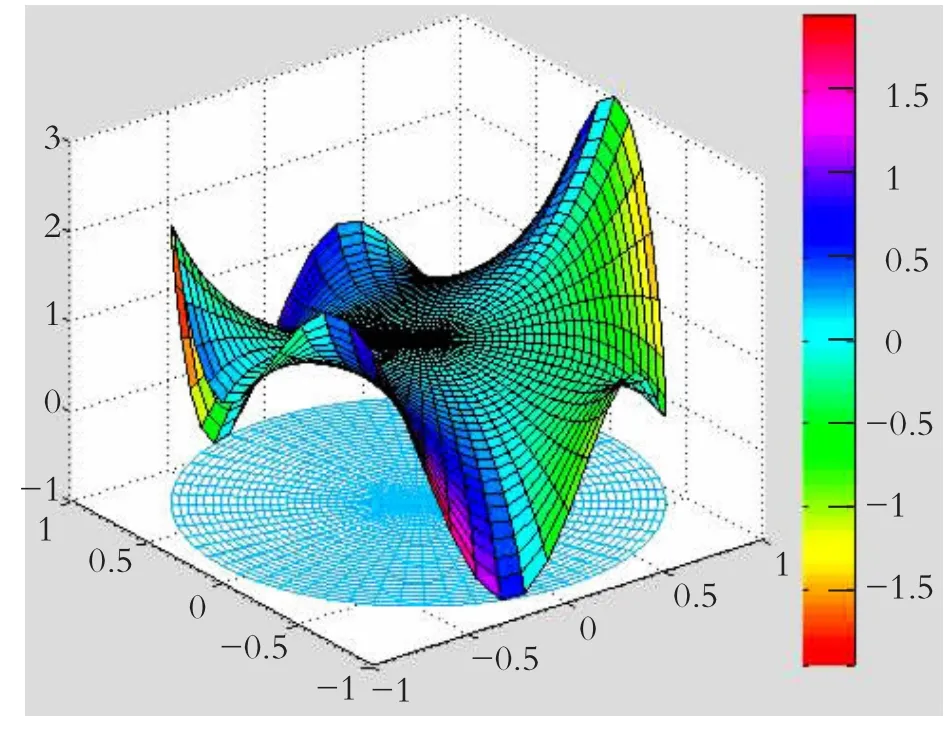
图3 复变函数f(z)=z5+z2+1的图像
对于某些解析函数,Taylor展开的方式方法虽然很多,但是计算较繁杂,而且Taylor展开式的结果也不一定很满意,但是在MATLAB的帮助下,这些工作就会很简单,调用函数就可以对其进行任意项的Taylor展开。
例:设f(z)=sin(z2/(z-1)),求f(z)在z=3处的前五项Taylor展开式。
MATLAB程序如下:
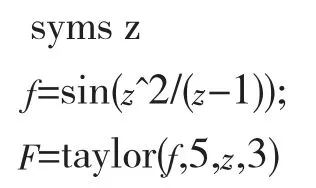
结果:
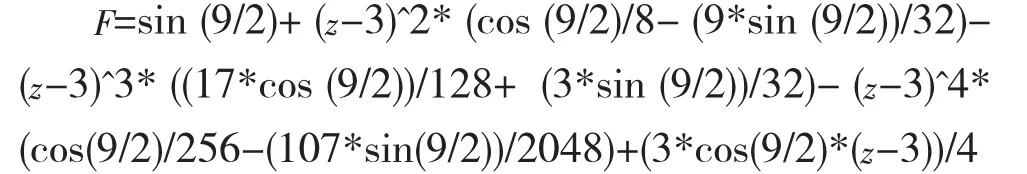
5 结论
基于高级程序设计语言强大的绘图功能,教师不需要在课堂上进行冗长的数学理论推导,只需要引导学生分析讨论解决问题的思路和处理方法,数学运算可交给数学专业软件去进行,不但减轻了教师的负担,而且有利于学生理解函数的概念及培养学生对于数学建模软件的应用能力,无论是对学生课程理论知识的学习,还是对学生数学能力和建模能力的提高都具有重要意义和实用价值。
