变工况刀具破损监测的半监督增量学习方法

孙世旭，胡小锋，夏铭远

(1.上海交通大学 机械与动力工程学院，上海 200240;2.上海航天控制技术研究所，上海 201109)

0 引言

刀具破损直接影响切削加工零件的表面质量，造成不可修复的表面损伤，甚至损坏机床。尤其对于航空发动机机匣、发电机转子等高价值零件，会导致巨大的经济损失。刀具破损在线监测在保证加工质量、降低加工成本方面具有重要意义。

近年来，国内外许多学者致力于刀具破损监测的研究。刀具破损失效主要有切削刃破损(flute breakage)和柄断裂(shank breakage)两种类型[1-2]，其中柄断裂属于最严重的刀具破损，很容易通过切削力、功率等信号检测；切削刃破损在本质上是细微的破损，因此很难检测[1]。在刀具破损机理和理论模型方面，李健男等[3]基于分子动力学分析了粘结破损的过程和原因；蒋宏婉等[4]基于近场动力学理论分析了冲击载荷引起的刀具微观破损机理和原因；郑敏利等[5]提出通过粘结自由能衡量刀具破损程度；程耀楠等[6]基于硬质合金抗弯强度理论，采用经验公式建立了硬质合金刀具理论寿命可靠性模型。研究刀具破损的机理和理论模型，有助于确定影响刀具破损的主要因素，但无法杜绝破损发生、避免破损刀具继续使用造成质量事故。

为了保证加工质量，在加工过程中通过振动[7-8]、功率[9-10]、声发射[11-14]等信号对刀具进行在线监测成为主流方法。然而，由于此类高值零件对制造过程的可靠性有严苛要求，且刀具破损会造成零件表面不可修复的损伤[15]，通常采用保守的切削参数和换刀策略将破损发生概率降至最低，导致能够获取的刀具破损样本数量远小于刀具正常状态的样本数量，机器学习模型无法充分学习到刀具破损信号的规律。此外，刀具内部裂纹的增加、扩展和刀具破坏形式都具有随机性[16-17]，刀具破损的信号复杂多样；生产环境中存在工件材料性能波动、切削参数微调等工况变化，刀具正常状态的信号分布随工况变化；导致基于历史样本建立的监测模型存在对破损的查全率低，对正常状态的误报率高的问题。

增量学习(incremental learning)[18]方法被提出用于应对机器学习中的概念漂移(concept drift)[19]，解决机器学习模型对分布变化样本的识别问题。ZHANG等[20]将自编码器分为两部分，在前三层用于提取样本的共有特征，后三层用于提取样本的私有特征，通过重建误差判断是否发生了概念漂移，发生概念漂移后对后三层进行学习和更新，从而避免增量学习过程的灾难性遗忘。LI等[21]提出一种不平衡数据增量学习的集成学习方法，通过训练多个决策树构建集成分类模型，在获取一定数量的新样本后，基于Bagging算法对新样本进行重采样以平衡其分布并划分为多个样本集，然后采用这些样本集对所有决策树进行训练，以更新集成分类模型。ZHU等[22]通过训练一系列极限支持向量机(extreme support vector machine)实现并行的增量学习，通过对这些极限支持向量机的结果加权相加得到最终结果，实验表明该方法取得了与批量学习一致的效果。然而，上述增量学习方法解决的是样本类别增加的学习问题，而不能处理同类样本分布变化的问题，且均基于监督学习，无法应对刀具破损监测中存在的样本极度不平衡问题。

本文提出一种刀具破损在线监测的半监督增量学习方法。首先，通过半监督学习机制对大量刀具状态正常的样本分布进行学习，在没有刀具破损样本参与训练的条件下，通过判断样本是否符合正常样本的分布规律实现破损样本的检测；然后，在刀具破损监测过程中，当出现样本分布变化或识别错误时，对模型进行增量训练，确保模型时刻具备良好的检测性能。

1 增量学习方法

机器学习模型在实际应用过程中面临一个重要问题：数据是随时间逐渐产生的，数据的分布规律也可能随时间变化。传统的机器学习方法采用批量训练的模式，一次性对大量样本进行学习后，用于识别与训练样本同分布的新观测样本。在面对实际的随时间产生的样本数据时，存在前期样本不足无法训练模型，后期样本变化后模型性能下降，重新训练模型效率低、难度大的问题。增量学习方法可以先通过少量样本的训练建立模型，然后在获取到新的样本后对模型进行更新，从而赋予机器学习模型动态学习新知识的能力。

增量学习方法的定义是根据给定的数据流样本s1,s2,…,st生成一系列模型h1,h2,…,ht[18]。其中：st为t时刻产生的有标签训练样本,

st=(xt,yt)∈n×{1,2,…,C};

(1)

ht为t时刻的模型：

ht:n{1,2,…,C},

(2)

ht仅依赖t-1时刻的模型ht-1和最近的p个训练样本st-p+1,st-p+2,…,st，p为增量学习样本数量的上限。

增量学习方法具有以下特点：①模型需要逐步更新，t时刻的模型ht基于t-1时刻的模型ht-1更新得到，而不是完全重新训练；②保留之前已学习到的知识，避免灾难性遗忘，即在模型更新后，保留对历史训练样本的识别能力；③每一次更新模型，只有有限的样本(数量为p)用来训练。

由于在模型对新样本进行识别后延迟一段时间即可获得样本的真实标签，大部分增量学习方法所用的样本都是有标签样本，其学习方法本质上还是监督学习，而且目前很少有考虑到数据极度不平衡的增量学习方法。在应用于刀具破损样本极少的不平衡问题时，很难从极少的刀具破损样本中学习规律，需要研究半监督的增量学习方法，以学习多数正常状态样本的分布规律为主，当出现破损样本、识别错误或者样本分布变化时，对模型进行更新。

2 刀具破损检测的增量学习方法

本文基于自编码器提出一种刀具破损监测的增量学习方法，该方法在生产过程中实施的流程如图1所示，图中最下方的横轴代表时间，上方的4层分别代表随时间产生的样本、发生的事件、采取的措施和得到的模型。本文提出的方法包含模型的初始训练阶段和破损检测与增量学习阶段两个主要阶段。

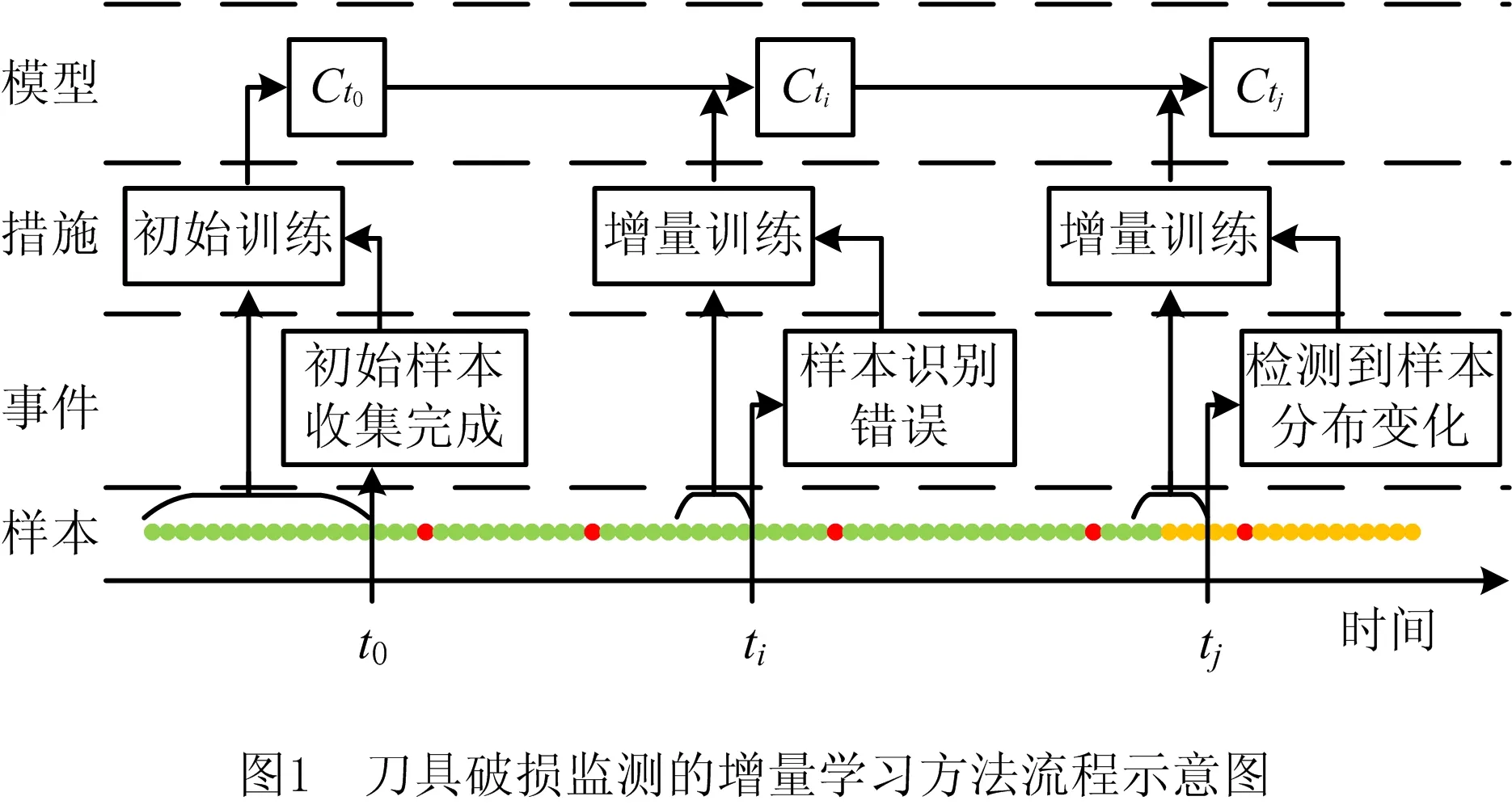
模型的初始训练阶段为离线完成，在收集到一部分刀具正常状态的样本后，即t0时刻，启动初始训练，自编码器网络学习刀具正常状态的样本分布规律，据此建立刀具破损检测的模型Ct0，模型的初始训练阶段完成，进入刀具破损检测和增量学习阶段。

刀具破损检测和增量学习阶段为在线完成，首先通过Ct0对新产生的观测样本进行识别，识别后延迟一段时间即可获得样本的真实类别标签。若出现样本识别错误，则触发增量学习，即ti时刻，模型自动抓取临近ti时刻的p个样本进行增量训练，模型由Ct0更新为Cti。模型在进行刀具破损检测的同时，检测刀具正常状态的样本分布规律是否与已学习到的规律一致，若出现较大偏差，即使没有样本识别错误，也会主动触发增量学习。如图1中tj时刻所示，模型检测到样本分布变化，自动抓取临近tj时刻的p个样本进行增量训练，模型由Cti更新为Ctj。

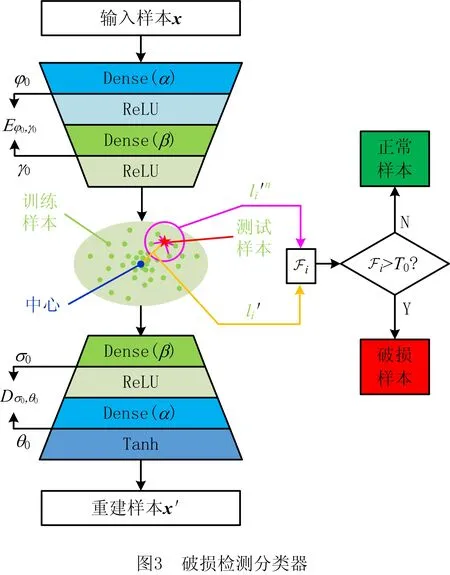
2.1 刀具破损检测的自编码器模型

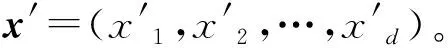
Eφ:Rd→Rk,x→Eφ(x)。

(3)

其中φ为编码器的网络参数。

将h映射为x′的部分网络称为解码器(Decoder)，记为：

Dθ:Rk→Rd,h→Dθ(h)。

(4)

其中θ为解码器的网络参数。

(5)

(6)

传统的自编码器网络用于异常检测等半监督学习问题时，仅以重建误差作为检测依据，当观测样本的重建误差超过已有正常样本的最大重建误差时，则判别为异常，否则判别为正常。在应用过程中存在对异常样本的检测率低、将分布发生变化的正常样本误判为异常等问题，且不具备增量学习能力。本文对现有的自编码器网络进行改进，设计新的损失函数和分类方法，并引入增量学习机制，以实现刀具破损的准确检测。

本文提出的刀具破损检测自编码器通过样本在低维特征空间的分布对样本进行识别，通过样本的重建误差判断样本分布是否发生变化。其结构如图2所示，包含4层，其中编码器Eφ,γ包含两层，其节点数分别用α,β表示，其网络参数分别用φ,γ表示；解码器Dσ,θ包含两层，其节点数与编码器对称，分别为β,α，网络参数分别用σ,θ表示。

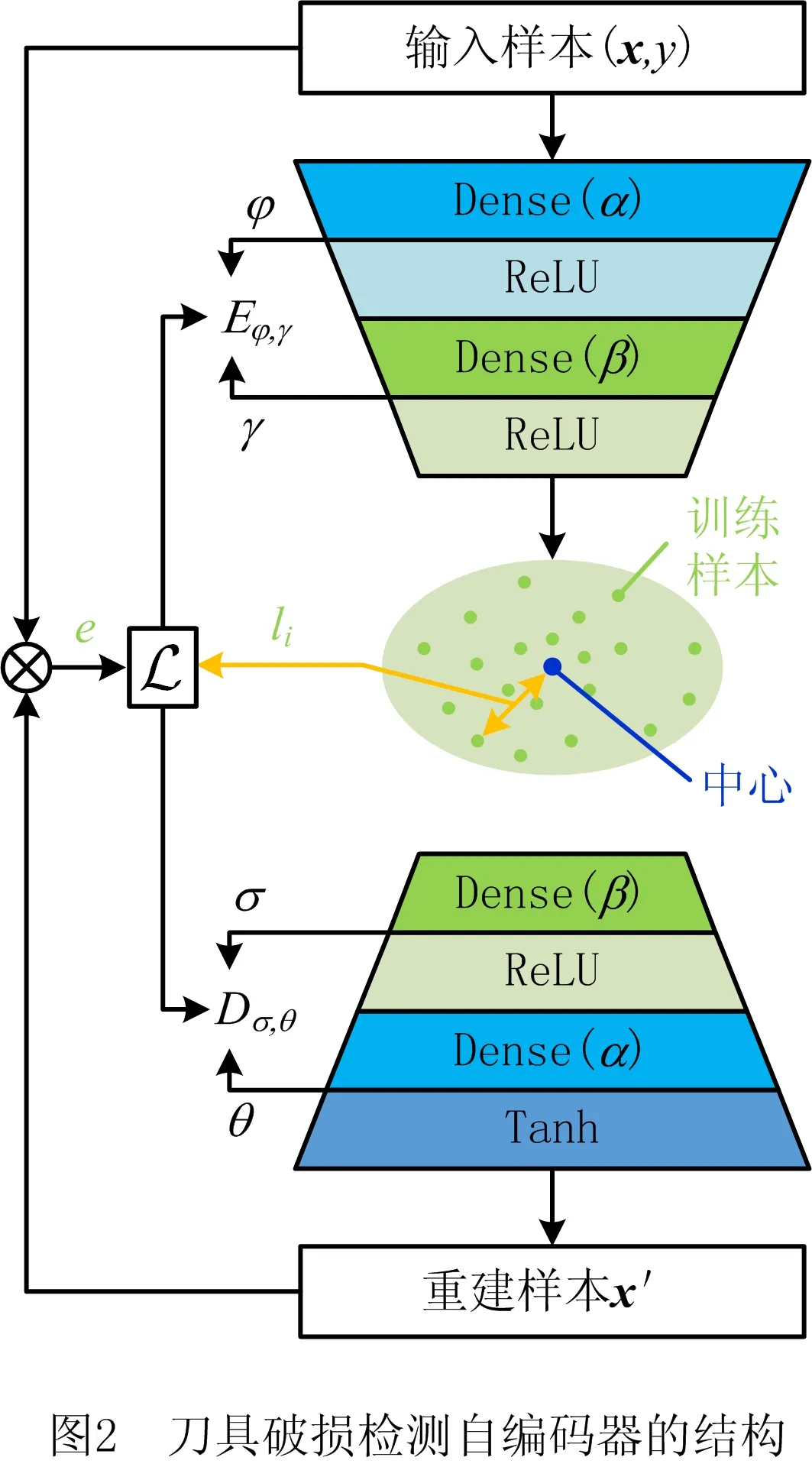
自编码器网络以(x,y)为输入，x=(x1,x2,…,xd)是d维样本，y∈{1,0}是样本的标签，刀具正常状态的样本标记为0，刀具破损的样本标记为1，样本的标签y仅在网络的训练阶段起作用，用于计算损失函数。

编码器的输出，即低维特征向量h的输出，用于进行刀具破损的检测；解码器的输出，即重建样本x′的输出，用于样本分布变化的检测。

2.2 模型的初始训练

在采集到一定数量的初始样本后，对破损检测的自编码器模型进行初始训练。初始训练的目标是以刀具正常状态的样本对自编码器进行训练，令自编码器学习正常样本的特征和压缩、重建的规律。在初始训练阶段，模型的损失函数为：

(7)

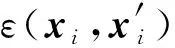
(8)

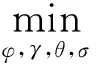
(8)

在完成初始训练后，将训练好的编码器和解码器记作Eφ0,γ0,Dσ0,θ0，用于破损检测和样本分布变化检测。

2.3 分类器构建和破损检测

破损检测的自编码器对样本进行压缩，提取的低维特征并不能直接用于破损检测，还需要根据样本的特征分布构建用于破损检测的分类器。

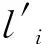
(10)

(11)

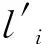
(12)

T0=min{μ0+C·σ0,max(0)}。

(13)

2.4 模型的增量学习

在完成模型的初始训练，进行破损检测的过程中，模型将同时检测样本的分布是否发生变化，若样本不符合训练样本的分布规律，则对模型进行增量训练。同时，若检测过程中出现样本识别错误，同样触发增量训练，使模型始终保持良好的检测准确性。

样本分布变化的检测通过样本的重建误差实现，对一个观测样本xi，根据式(6)计算其重建误差εi，若大于训练样本的最大重建误差εmax，即εi>εmax，则判断为样本不符合训练样本的分布，进行增量训练。初始训练阶段，参与训练的只有正常样本，损失函数ini也是针对正常样本设计的。在增量训练阶段，破损样本也可能参与增量训练，因此需要修改损失函数。在增量训练阶段，模型的损失函数为：

(14)

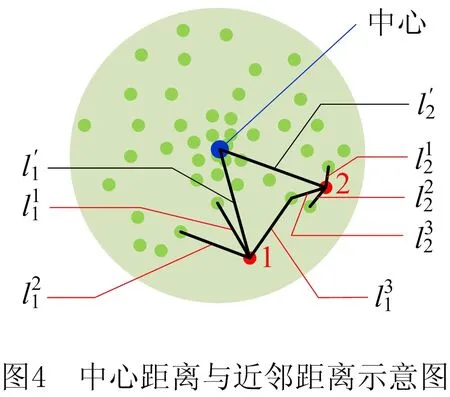
式中：p为参与增量训练的样本数量;ε(x,x′)为式(6)所示的样本重建误差;N0,N1分别为增量训练样本中标签0和1的样本数量;L0,L1分别表示标签为0和1的样本与中心的距离平方和：

(15)

(16)

式中li为式(8)所示训练样本距离样本中心的距离。L0的作用与初始训练时一致，促使正常样本的特征分布集中；L1的作用是促使破损样本的特征远离正常样本。

在增量学习阶段，为保留模型对与初始训练样本同分布样本的识别能力，将编码器第一层、解码器第二层的网络参数φ0,θ0固定，只更新编码器的第二层和解码器的第一层。即增量训练过程通过最小化损失函数优化Eφ0,γ,Dσ0,θ：

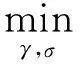
(17)

在完成自编码器的增量训练后，还需将参与增量训练的样本并入初始训练样本集，并根据式(13)重新计算破损识别分类器的阈值T0，然后继续进行破损检测和样本分布检测。

3 应用实例

3.1 实验数据

本文实验平台由某发电机厂提供，采用某型号转子嵌线槽铣削加工过程刀片破损监测数据[24-25]，测试和验证本文所提方法。该实验数据包含5次发电机转子的加工过程监测数据，5次实验的工件材料均为25Cr2Ni4MoV，工件的材料性能实测数据如表1所示，对每个工件的6个不同位置进行采样，测试得到屈服强度和抗拉强度的均值和标准差；切削刀具为直径1 100 mm的槽铣刀，上面安装36个SNC55型硬质合金刀片作为切削刃；切削条件为转速35 RPM，进给速度350 mm/min，切削深度50 mm，切削宽度42.1 mm，采用空气冷却。

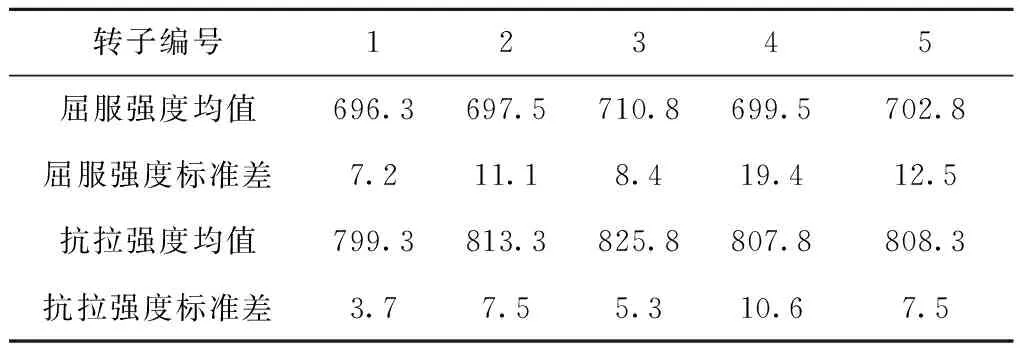
表1 工件的材料性能 MPa

转子的加工和数据采集过程如图5所示，在加工过程中，采用声发射传感器监测刀具状态，传感器型号为PAC-R15α，通过磁座吸附固定在工件表面。信号的采集设备为PAC-PCI2型声发射信号采集卡，采样频率为2 MHz，通过采集卡实时提取均方根值、幅值、上升时间、绝对能量、平均信号电平、计数、峰值计数、信号强度、平均频率、中心频率、初始频率、峰值频率、反算频率13个特征值。

实验完成后，采用工业视频显微镜测量刀片的破损大小，显微镜的放大倍数为160倍，测量分辨率为1 μm，如图6所示。在本实验中，共采集到17个破损样本和10 433个刀具正常状态的样本，用于对本文提出的方法进行测试和验证。

3.2 实验设计

将实验数据集按照样本获取的时序和工况，分为初始训练样本和测试、增量学习样本两个子集。其中，初始训练样本集中包含2 250个刀具正常状态的样本，无刀具破损的样本，所有样本均在1号转子加工过程中采集。测试、增量学习样本在2号～5号转子的加工过程中采集，包含8 200个样本，其中17个刀具破损状态的样本，8 183个刀具正常状态的样本。

首先，采用初始训练样本训练刀具破损检测的自编码器，并构建破损识别分类器。本文设计的自编码器网络通过TensorFlow[26]构建，采用学习率为lr的Adam[27]优化器进行训练。初始训练阶段是离线进行的，编码器网络每次从初始训练样本集中随机抽取Nb个样本进行训练，重复Ne次。Nb,Ne以及前文提到的关键参数的取值如表2所示。本文设计的自编码器网络的结构和关键参数是根据文献[28]～文献[29]中的经验设置的，表中给出的取值为效果最好的。

表2 关键参数设置

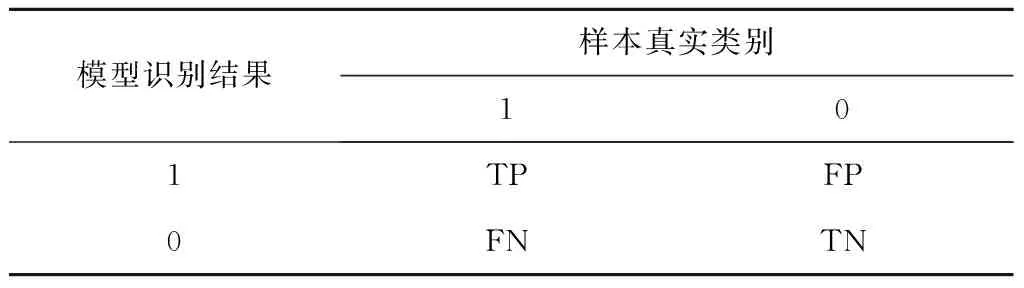
表3 识别结果的混淆矩阵

然后，根据混淆矩阵计算模型对所有测试样本的正确率A、查全率R、查准率P和F得分F1：

(18)

(19)

(20)

(21)

其中：正确率衡量的是模型正确识别所有样本的能力；查全率衡量的是模型正确识别正类(即少数的破损样本)的能力；查准率衡量的是模型正确识别负类(即多数的正常样本)的能力；F得分是查全率和查准率的调和平均值，综合衡量模型的查全率和查准率。

3.3 破损检测结果

根据测试样本的检测结果，按样本采集的顺序逐个增加样本，计算样本量增加时模型的正确率、查准率、查全率和F得分，并绘制各评价指标的变化趋势，如图7所示。图中，不同颜色、线型的曲线代表各评价指标随累计样本数量的变化情况，例如，红色线条上的点(2 000,100)代表本方法对累计获取的2 000个样本的查准率为100%；为了便于分析本方法的表现，用黑色线条标注了触发增量学习的时刻。测试样本的真实类别标签如图8所示，其中绝大多数样本为刀具正常状态的样本，刀具破损的样本仅17个。

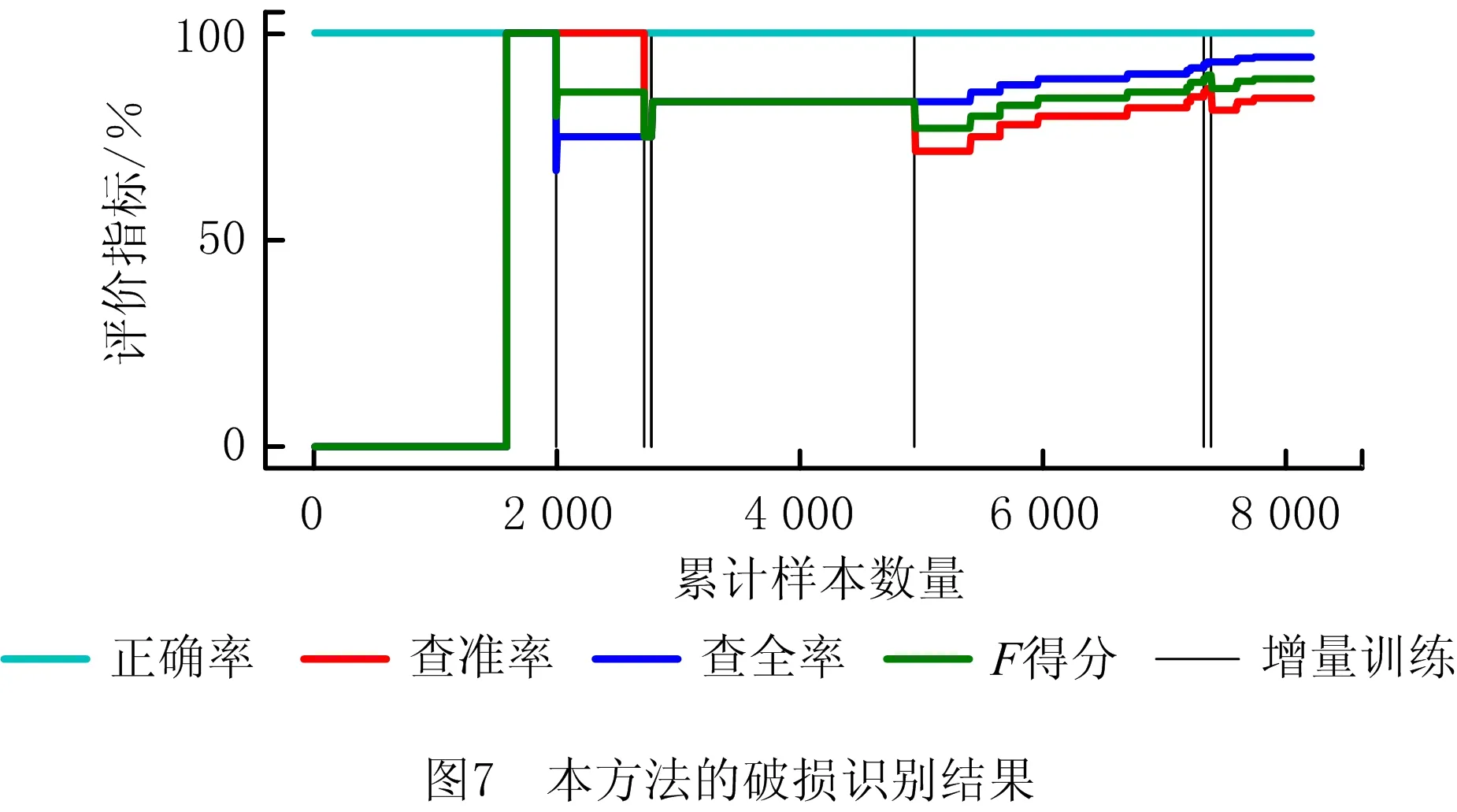
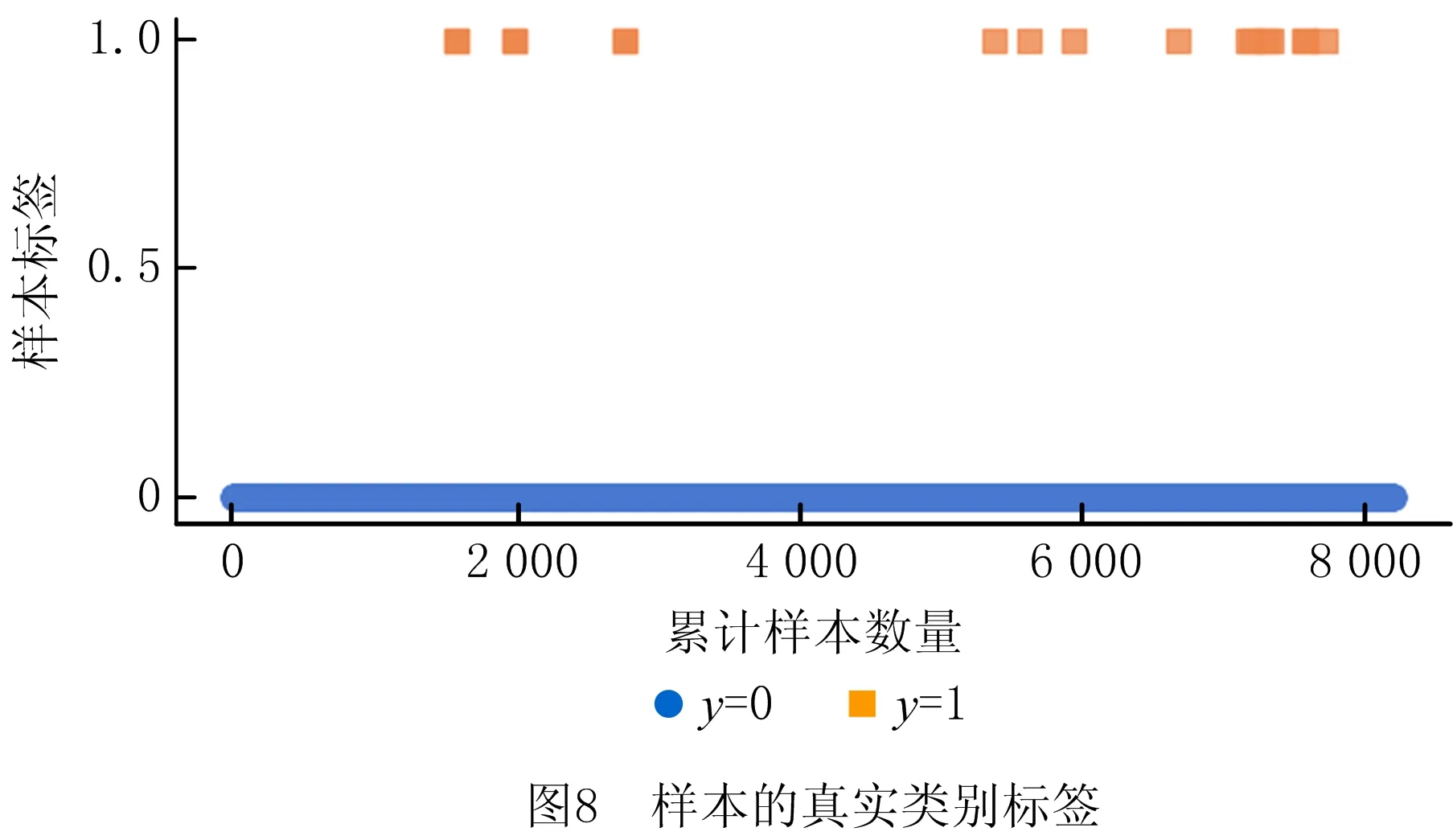
在刀具破损的观测样本获取之前，准确率达到了100%，但查准率、查全率、F得分均为0，这是因为此时只有正常样本，所以对破损样本的查全率、查准率均为0，综合反映查全率和查准率的F得分也为0。在获取到刀具破损的观测样本，即累计样本数量大于约1 800之后，查准率、查全率、和F得分开始反映模型对刀具破损样本的检测效果。在获取到约2 000个样本时，模型对破损样本识别错误，查全率下降，在触发增量学习后破损的查全率提高；在获取到约2 700个样本时，模型对正常样本识别错误，查准率下降，在触发增量学习后查准率明显提高；随后在获取到约2 800个样本时，模型发现正常样本的重建误差仍大于历史样本的最大值，即发现样本分布变化，增量学习后模型的查全率、查准率等进一步提高；随着累计样本数量继续增加，又触发3次增量学习。

本方法一直保持较高的查全率和查准率，对所有样本的检测正确率始终保持在接近100%水平。最终，对所有8 200个测试样本的检测结果为：正确率99.95%，查准率84.21%，查全率94.12%，F得分88.89%。

3.4 与其他方法对比

为了客观评价本文提出方法的效果，本节采用相同的评价指标，将本方法与其他方法进行对比。本方法首先改进了标准自编码器的学习目标和破损检测方法，又引入了增量学习机制，因此本节将标准自编码器和改进的自编码器作为对比方法。除自编码器方法以外，其他常用于半监督异常检测问题的方法，按机理主要可以分为基于概率的(probabilistic)、基于域的(domain-based)、基于距离的(distance-based)和基于重建的(reconstruction-based)[32]。其中，基于概率的方法对高维样本效果很差[32]；本文所提方法是基于重建的，将本方法与基于重建的代表性方法——标准自编码器、基于域的代表性方法——一分类支持向量机 (one-class support vector machine)、基于距离的代表性方法——局部离群因子 (local outlier factor)进行对比。

标准自编码器与本方法采用相同的网络结构，采用式(5)所示的损失函数，将训练样本的最大重建误差作为破损识别的阈值，采用样本的重建误差对样本进行识别。其识别结果如图9所示，该方法对所有样本的检测正确率较高，但查全率、查准率较低，且存在多次下降的问题。对所有8 200个测试样本的检测结果为：正确率99.60%，查准率19.23%，查全率29.41%，F得分23.26%。

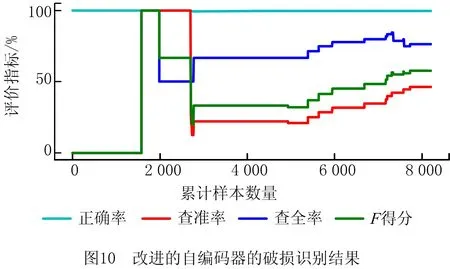
改进的自编码器与本方法采用相同的网络结构和主要参数，同样采用式(7)作为损失函数，采用式(12)和式(13)进行破损样本识别，与本方法的唯一区别是在测试过程中不检测样本分布变化，也不进行增量学习。其识别结果如图10所示，该方法对所有样本的检测正确率接近100%，查全率、查准率相比标准自编码器有提高，但仍存在随样本数量增加而下降的问题。对所有8 200个测试样本的检测结果为：正确率99.77%，查准率46.43%，查全率76.47%，F得分57.78%，效果不如增量学习方法。

一分类支持向量机采用径向基核函数(radial basis function)，其超参数松弛变量参数nu和gamma通过指数变化的网格搜索确定最优参数组合，即nu=0.05∶0.05∶1,gamma=2-10∶1∶5。其识别结果如图11所示，该方法将大量正常样本错误识别为破损，导致其总体正确率、查准率、F得分极低，仅对破损的查全率正常，为47.06%。

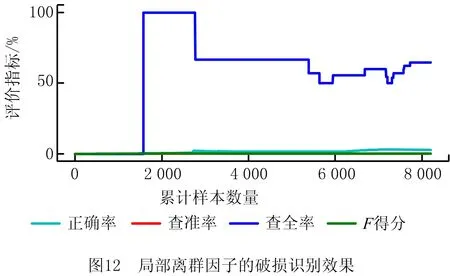
将局部离群因子的超参数n_neighbors设置为{10,20,30,40,50,60,70,80,90,100}，选取最好的结果作为对比。其识别结果如图12所示，与一分类支持向量机类似，该方法将大量正常样本错误识别为破损，其总体正确率、查准率、F得分极低，仅对破损的查全率略高，为64.71%。

本文提出的增量学习方法与其他方法最终对所有测试样本的识别结果如表4所示。本文所提方法获得了94%的查全率和84%的查准率，相比于改进的自编码器，即无增量学习机制的方法，将查准率从46%大幅提高至84%，将查全率从76%进一步提高至94%；相比于标准的自编码器方法、一分类支持向量机和局部离群因子方法，在查全率、查准率方面均有大幅度提高，在4个评价指标上均取得最优结果(如表中加粗字体所示)，证实了本文提出的增量学习方法可以有效提高模型对不同工况获取的样本的识别能力。

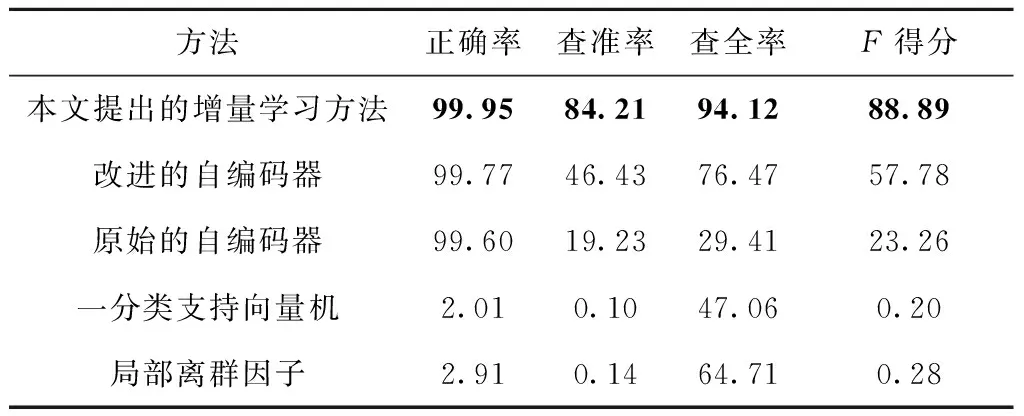
表4 5种方法的破损识别结果 %

4 结束语

实际生产环境中获取的刀具破损样本数量远小于正常样本数量，且生产环境中存在工况变化导致刀具正常状态的信号分布变化，基于历史样本建立的监测模型查全率低、误报率高的问题，本文提出一种基于半监督学习的增量学习方法，首先采用一部分刀具正常状态的样本对模型进行初始训练并开始刀具破损检测，在检测过程中同时判断样本分布是否变化，在样本分布变化或者模型识别错误时对模型进行增量训练，使模型时刻具有良好的检测能力。相比于无增量学习机制的方法，本文方法将查全率从76%提高至94%，查准率从46%提高至84%，显著提高了对不同工况获取的样本的识别能力。

在未来工作中，需要进一步研究将反映工况变化的材料力学性能等数据输入模型中，为模型提供更多信息，从而实现更好的刀具破损检测效果。