考虑绝缘性能的变频调速电机轴承优化设计

贾正阳，宋俊杰+，汪久根，洪兆溪，冯毅雄，李学军，黄元通，郝 旭，谭建荣

(1.浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027；2.佛山科学技术学院 机电工程与自动化学院，广东 佛山 528225；3.成都中车电机有限公司，四川 成都 610511；4.瓦房店轴承集团有限责任公司，辽宁 瓦房店 116300)

0 引言

滚动轴承的性能优劣直接影响着城市地铁牵引电机、电气化铁路牵引电机等电机的功能与质量，是机械装备中重要的核心基础件。随着变频器驱动技术的不断发展与完善，交流变频电机在工业领域的使用日益广泛，其中使用频率最高的种类就是变频调速感应电机。但是对于这些大功率、变频、高压防爆的交流变频电机，水利、火力、风力发电机，高速轨道列车牵引电动机等设备，大多数情况下其内部的电机轴承的主要失效形式为电蚀[1-2]。电蚀是轴承常见的损伤形式之一，牵引电机在正常工作时，电机系统内部常常会出现由磁路不平衡原因引起的低频轴电流和伴随逆变器变频驱动的共模电压导致的高频泄漏电流等，这些电流会沿着机座、转轴和轴承之间形成环路电流[3]。当电流经过轴承时，会在轴承内、外套圈之间产生电压，当电压足够大时会击穿润滑油膜的最薄弱点，形成闭合回路，电流会流过轴承内部，甚至产生电火花，导致接触表面出现局部熔融损坏，此时其轴承表面会出现密密麻麻的小凹坑，即发生电蚀[4]。若轴承继续运转，其振动与温升均会迅速增大，轴承很快会失效，而电机及相关设备也可能出现不可预期的伤害，并伴有重大损失。另外，电蚀还会造成润滑油脂的变质变色[5]，使其丧失应有的润滑能力，严重时会损坏转轴和轴承[6]。

随着高频交流电机技术的发展，国外各大轴承的制造厂商均开始研发满足各类工况要求的绝缘轴承，这些厂家不但将其绝缘轴承产品推向市场，而且还将其应用到各国的重要领域。例如瑞典SKF公司生产了INSOCOAT系列绝缘轴承[7]，并将混合陶瓷球绝缘轴承应用于风电发电机中，大大降低了该电机中轴承失效的概率[8]。日本NTN公司生产了MEGAOHMTM系列绝缘轴承，并将树脂覆膜绝缘轴承和陶瓷涂层绝缘轴承分别应用于本国的普通轨道车辆与新干线中。同时，我国CRH3及CRH380HL型动车组牵引电机中也均使用了陶瓷涂层绝缘轴承，为列车运行的稳定性及进一步提速提供了保障[9]。陶瓷喷涂绝缘轴承是最常见的一种绝缘轴承，通常采用等离子喷涂方法在轴承的内、外套圈外表面及侧端面制备一种高绝缘性的陶瓷涂层，以实现轴承绝缘，防止电蚀现象发生[10]。该类绝缘轴承不仅具有高温下良好绝缘性和耐磨耐腐蚀性，还具有较优的尺寸稳定性，可制备各尺寸类型的轴承，并可加工至所需精度要求，实际应用中可与普通电机轴承相替换[11]。

目前，已经有很多学者对轴承的电蚀失效机理和抑制策略进行了大量的研究。NOGUCHI等[12]和汪久根等[13]以线接触副轴承和齿轮为研究对象，采用分形方法模拟三维粗糙表面，建立粗糙表面的矩形斑点接触电阻计算模型和电流密度计算模型，结果表明增加轴承和齿轮表面间的接触载荷和减小表面粗糙度可以防止电蚀的发生，但是并未验证绝缘轴承绝缘层厚度、滚动体直径等结构参数对于轴承寿命的耦合影响。ADABI等[14]和刘瑞芳等[15]对电机内部耦合电容参数的准确计算和测量进行了研究，采用有限元法对异步电机进行多导体系统耦合电容分析计算，提出了定子绕组电磁散线建模方法，大大减小了定子绕组和定子机壳之间电容的计算误差，但是并未基于轴承结构参数提出有效的轴承电蚀抑制方法。TIWARI等[16]和侯伟[17]基于粒子群优化算法对轴承建立了多目标优化模型，证明了多目标优化算法在轴承优化设计问题中良好的运用效果，但是并没有考虑轴承的电学损伤机制，且在实际工程应用中容易出现早熟收敛、陷入最优化局部陷阱等问题。

综上所述，现有文献针对牵引电机滚动轴承的电蚀问题，已从产生机理、抑制方法、电机结构优化等不同角度展开了深入的研究，并取得了一定的成果，但是鲜有文献从轴承结构参数优化设计的角度对轴承电蚀的抑制和轴承寿命的提高进行研究。此外，以提高轴承性能为目的，基于多目标优化算法的轴承优化设计较为成熟，但是现有文献较少结合轴承电蚀寿命作为优化目标实现轴承的优化设计，且所采用的多目标优化算法存在多样性差、局部收敛等缺点。因此，本文针对变频调速电机绝缘轴承提出优化设计方法，主要研究内容包括：

(1)对某款装载陶瓷喷涂绝缘轴承的地铁牵引电机进行仿真建模和电路拓扑，分析计算轴承绝缘层厚度对牵引电机耦合电容和轴承电流的影响机制。

(2)分析绝缘层厚度、滚动体直径、滚动体个数、节圆直径等参数对绝缘轴承的机械、电蚀耦合寿命和表面硬度的影响效果，建立多目标优化模型。

(3)在NSGA-Ⅱ算法基础上引入改进策略，提升种群的收敛性和多样性，并验证改进后算法的优越性。将这种设计方法应用于实际工程中的绝缘轴承优化设计，能够避免选取参数时的人为因素影响，获得比常规设计更佳的设计参数，使绝缘轴承拥有更好的工作性能。

1 变频调速电机绝缘轴承电学损伤机制分析

1.1 变频调速电机耦合电容分析

变频调速牵引电机是地铁车辆将电能转换为牵引力的重要部件，电机的轴承故障直接影响行车安全和运营服务水平，但是由于地铁车辆复杂的电气环境，使得判断地铁牵引电机轴承电流的构成和来源十分困难。以北京地铁房山线所配备的YQ-190地铁牵引电机为例，电机简化结构图如图1所示，电机定转子与其他部件之间的寄生电容是电机内部轴电流环路的主要元器件。目前，电机耦合电容的计算方法多采用基于独立平板电容器的解析计算方法[18]，该方法较为方便快捷，但是实际工作环境下的电机中存在多个等效电极，整个电机形成一个多导体系统，采用基于有限元软件的数值计算得到的耦合电容计算结果与实际测量电容值之间的误差更小[19]。在该牵引电机中主要有定子绕组、转子绕组(导条)、转子铁心(转轴)、定子铁心(机壳)4种导体电极，其中绕组与铁心之间由槽内DMD绝缘材料分开，定子和转子之间由空气隔开，由此可得该牵引电机内主要存在的寄生电容数量为6，分别由以上4个导体两两感应形成。在异步牵引电机当中主要考虑定子侧变流器共模电压的作用，转子绕组的影响可以被忽略，即主要考虑定子绕组与定子铁心之间的耦合电容Cwf、定子绕组与转子之间的耦合电容Cwr、定子铁心与转子之间的耦合电容Crf。

1.2 变频调速电机轴电流模型

变流器由于脉冲宽度调制(Pulse Width Modulation, PWM)供电方式产生的共模电压Vcom主要受变频器脉冲调制方式的影响，随之通过上述牵引电机中的复合耦合电容产生共模电流。在共模电流对耦合电容充放电的过程中，会在牵引电机的转轴与机壳之间感应出电压，该电压即为轴承内圈和外圈之间的轴电压Vb。地铁牵引电机简化的轴电流等效电路如图2所示[20]，其中Cbg为轴承润滑油膜未被击穿时润滑油膜两端形成的电容。

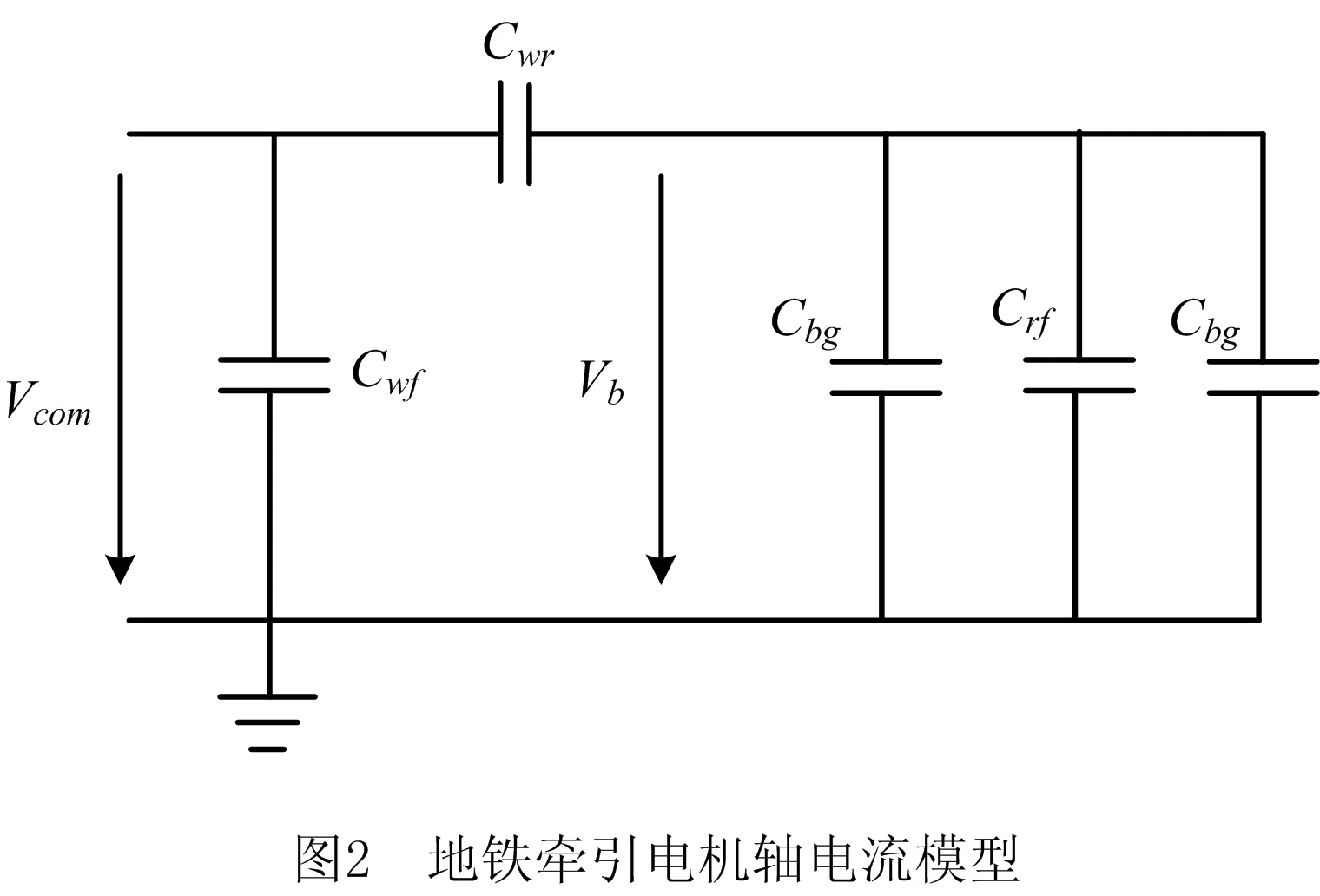
当轴承润滑油膜两端的分压小于其击穿电压时，轴承上只流过较小的dv/dt容性电流，该电流对轴承寿命基本无影响[21]；当轴承润滑油膜两端的分压大于其击穿电压时，润滑油膜被击穿并产生瞬间的电火花加工(Electrical Discharge Machining, EDM)电流，造成轴承电蚀。

针对YQ-190地铁牵引电机的结构和材料进行有限元仿真，如图3a和图3b所示，单个定转子对划分所得网格与电动机整体划分的网格密度差别不大；如图3c和图3d所示，电势强度从加压转子沿着绝缘套和气隙到接地定子逐渐降低。计算得到单个定转子对形成的耦合电容乘以定转子对个数与整个电动机形成的耦合电容基本相等，其中整个牵引电机计算得到的耦合电容值如表1所示。

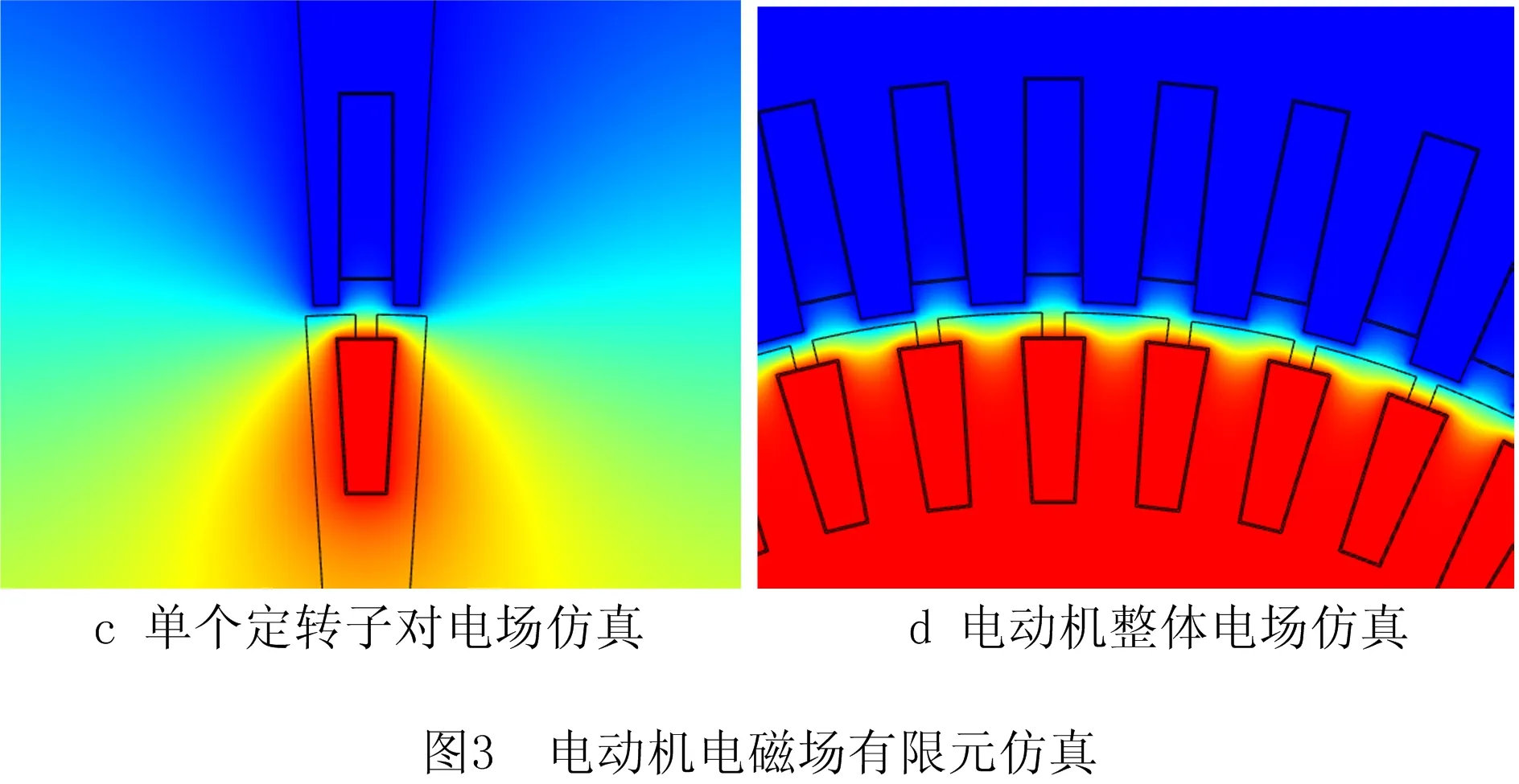
表1 YQ-190地铁牵引电机耦合电容

1.3 加入绝缘轴承的变频调速电机轴电流模型

在传统的电机轴电流模型的基础上，针对陶瓷喷涂绝缘轴承进行轴电流影响因素分析，该轴承与普通轴承的区别在于轴承外圈外环面添加了一层Al2O3绝缘材料。添加该绝缘层之后，可以有效减少轴承润滑油膜两端分压，降低润滑油膜被击穿产生EDM电流的概率，预防轴承电蚀失效。为了研究加入绝缘层之后对轴电流的抑制效果，对原牵引电机轴电流模型进行优化。由于只有在润滑油膜被击穿的EDM放电情况下，轴承寿命受电流影响较为明显，则地铁牵引电机轴电流等效电路如图4所示，其中Ci表示轴承外圈绝缘层电容。

根据如图4所示的轴电流等效电路，在轴承润滑油膜被击穿时轴承的对地电压Vb与共模电压Vcom的比值为轴承分压比，

(1)

式中：Vb为轴电压；Vcom为共模电压；Cwr为定子绕组与转子之间的耦合电容；Crf为定子铁心与转子之间的耦合电容；Ci为绝缘层电容。

由于绝缘层厚度相对轴承半径来说非常薄，采用平板电容器式(2)来替代圆柱形电容器公式计算绝缘层的电容Ci。在轴承型号确定的情况下，轴承内径、外径、宽度等参数都已确定，轴承外圈环面面积也无法改变，因此想要从结构角度优化绝缘层电性能，只能以绝缘层厚度为目标。

(2)

式中：ε0为真空介电常数；εr为绝缘层相对介电常数；D为绝缘轴承外径；b为绝缘轴承宽度；di为绝缘层厚度。

1.4 绝缘轴承润滑脂击穿电流仿真计算

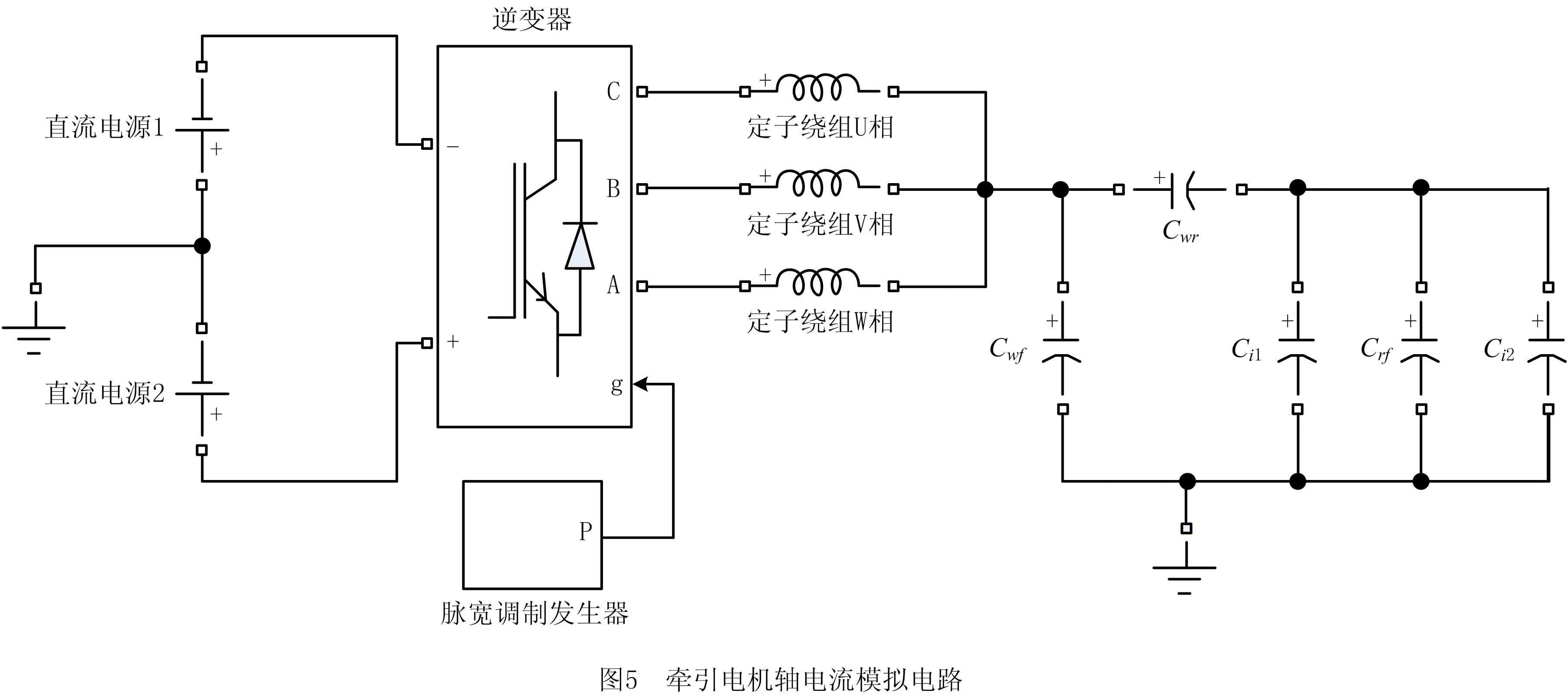
为了更好地确定轴承绝缘层对于牵引电机轴电流的影响效果，对牵引电机整体结构进行电路拓扑和仿真分析，在分析软件中根据上文建立的地铁牵引电机EDM轴电流模型建立模拟电路，如图5所示。

为了分析绝缘轴承绝缘层厚度，对于牵引电机中轴电流的影响，需要分析不同厚度绝缘层在仿真模型中的仿真结果，总结绝缘层厚度对轴电流的影响规律。现取8组轴承绝缘层厚度，并分别计算出其电容数值，如表2所示。

表2 不同厚度绝缘层的电容

将表3中的某牵引电机数据作为仿真电路的输入参数。

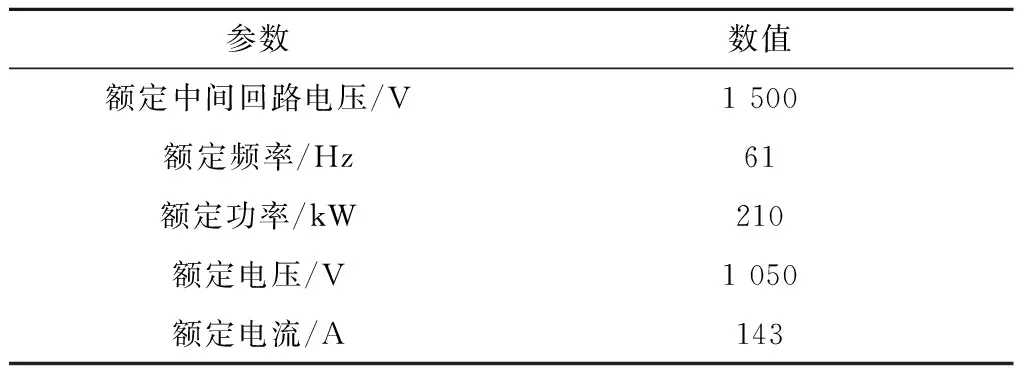
表3 某牵引电机参数

运行仿真电路0.03 s得到牵引电机当中的轴电流波形如图6所示。

由于本文主要针对轴承的电蚀问题进行研究，只要记录波形图中的轴电流极值，即可视作轴承工作过程中的最大EDM电流。针对8组喷涂了不同厚度绝缘层的绝缘轴承，分别仿真得出牵引电机中的轴电流，其中最大EDM电流值如表4所示。

表4 不同厚度绝缘层对应牵引电机EDM电流极值

根据表4中数据点，使用多项式拟合法得到EDM电流极值随绝缘层厚度的变化曲线如图7所示。

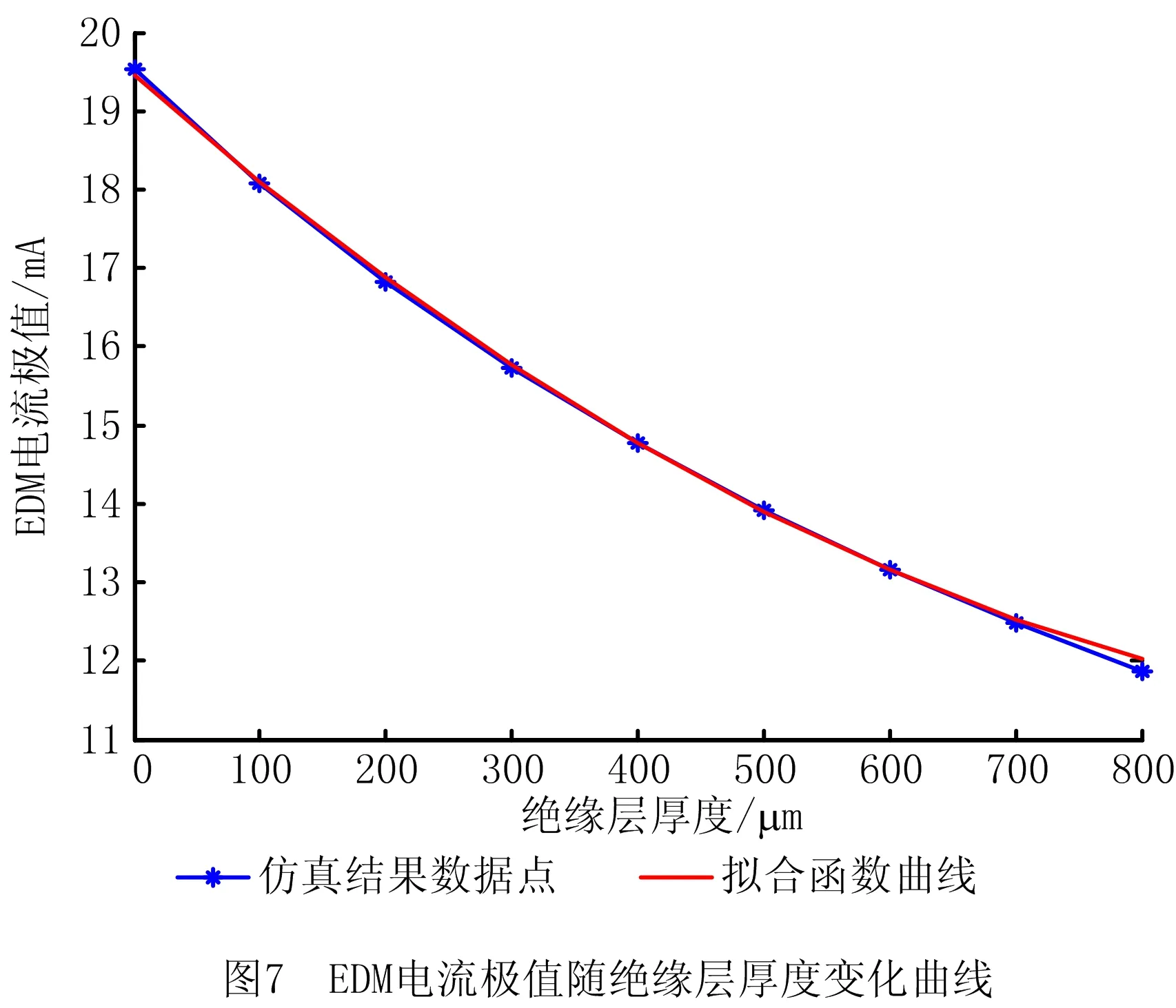
图7中拟合曲线对应的轴承绝缘层厚度di与EDM电流极值之间的关系函数如下：

(3)

2 绝缘轴承多目标优化设计模型

2.1 设计变量

本文研究的绝缘滚动轴承是一种在轴承外圈外表面喷涂氧化铝绝缘材料薄层的绝缘轴承，如图8所示，要求实现与现有设备上的传统滚动轴承直接替换，因此绝缘轴承与普通轴承的主要外形尺寸(如内径，外径和宽度)应该保持一致，无法对这些参数进行修改。但是滚动轴承内部的一些几何参数和绝缘层厚度并没有统一的设计标准，在轴承的基本型号确定之后，可以在一定区间内自由选取这些参数的数值，绝缘轴承优化问题主要对这些参数进行校核和优化。

选取绝缘层厚度di，滚珠直径Db，节圆直径Dm，每列滚珠个数Z，内沟曲率系数fi，外沟曲率系数fo6个参数作为优化设计变量。

[di,Db,Dm,Z,fi,fo]。

(4)

2.2 目标函数

目标函数是基于设计变量对优化目标的数学描述，可以判断优化方案的优劣。针对绝缘轴承在变频调速电机复杂工况下的综合性能，在抑制传统力学疲劳损伤的基础之上，需要防止电蚀损伤导致的轴承失效，还要避免绝缘层在拆装过程中剥落。选取疲劳寿命、电蚀寿命、绝缘层表面硬度3个优化目标。

(1)疲劳寿命

在高速滚动轴承运行过程中，由于轴承滚道和滚珠的材料疲劳特性，滚动轴承最终一定会损坏失效。滚动轴承中滚珠与滚道表面的接触载荷随所受力矩、接触角、转速等众多因素影响，一般首先在接触表面形成较小的初始裂纹，由于载荷循环往复的作用，裂纹会迅速扩展，使得接触表面金属材料呈鱼鳞状剥落，最终发生滚动疲劳，达到使用寿命。以绝缘轴承的疲劳寿命作为优化目标之一。

(5)

式中：Lf为轴承疲劳寿命;fc为绝缘轴承结构系数；i为绝缘轴承滚子列数；α0为公称压力角；Z为每列滚珠个数；Db为滚珠直径;Fr为径向载荷；Fa为轴向载荷；X为径向载荷系数；Y为轴向载荷系数。

(2)电蚀寿命

高速牵引电机中常见多数轴承失效主要原因是轴承的电蚀损伤，装配有绝缘轴承的PWM调频异步牵引电机中仍存在充放电流击穿润滑油膜，导致绝缘轴承电蚀失效。绝缘层的厚度、轴承所受载荷都会影响轴承滚珠与滚道之间通电时对轴承滚道的损伤程度。使用电蚀寿命作为另一个优化目标[22]。

Le=7 867 204×10-(2.17Jb)，

(6)

(7)

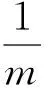
(3)绝缘层表面硬度

从抑制轴电流的角度考虑，增加绝缘轴承绝缘层的厚度即可减小绝缘层电容，也可以降低流过润滑油膜的电流，削弱电蚀损伤。但是随着绝缘层厚度的增加，轴承外圈外表面基体的加热时间也会变长，基体与涂层间的内应力会增大，导致基体与涂层之间的结合力下降，涂层表面硬度也会下降，使得绝缘轴承在安装、卸载和冲击情况下更易出现龟裂和掉块情况。使用绝缘层表面的显微硬度作为最后一个优化目标[23]。

(8)

式中：MHV0.2为绝缘层表面硬度；di为绝缘轴承的绝缘层厚度。

2.3 约束条件

约束条件是判断求解得到的优化方案是否可用的必要限制，任何可行方案必须满足其要求。在轴承类型已知的情况下，内径、外径和宽度已经确定，作为设计变量的结构参数由于工作环境和拆装条件的限制必须满足一定条件。

(1)绝缘层厚度

喷涂在轴承外圈外表面的绝缘层为满足不被1 000 V电压击穿，厚度应不小于200 μm[24]；为满足与基体的结合强度和装卸变形强度，厚度应不大于800 μm。绝缘轴承绝缘层厚度应满足如下约束：

200 μm≤di≤800 μm。

(9)

(2)滚珠直径

为了满足轴承内圈安装和实际工程需要，绝缘轴承滚珠直径应满足如下约束：

(10)

式中：KD为滚珠球径约束条件系数，D为绝缘轴承外圈直径，d为绝缘轴承内圈直径。

(3)节圆直径

为保证绝缘轴承运行过程中的旋转灵活度，轴承节圆直径与轴承的平均直径不能相差过大，且在优化过程中，节圆直径应大于轴承的平均直径。绝缘轴承节圆直径应满足如下约束：

0.5(D+d)≤Dm≤(0.5+a)(D+d)。

(11)

式中:Dm为绝缘轴承节圆直径,a为节圆直径系数。

(4)每列滚珠个数

考虑到轴承内圈的安装过程，同列的滚珠之间一定要留一定的间隙，使得同列滚珠紧挨在一起时的填球角满足要求。绝缘轴承每列滚珠个数Z应满足如下约束：

(12)

式中fmax为最大填球角(单位：°)，为装配经验值。

(5)内、外沟曲率系数

沟曲率系数用于描述钢球与滚道的密接程度，沟曲率系数越大，承载能力越小，摩擦也越小，同时会影响流过轴承的轴电流密度。绝缘轴承的内、外沟曲率系数应满足如下约束：

0.515≤fi≤0.53；

(13)

0.515≤fo≤0.53。

(14)

其中：fi表示绝缘轴承的内沟曲率系数，fo表示绝缘轴承的外沟曲率系数。

3 改进的NSGA-Ⅱ算法

3.1 算法改进策略

传统的多目标遗传算法存在单位时间内搜索到帕累托最优解数量较少、离散型变量编码困难的问题，带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)采用快速非支配排序方法和拥挤比较算子，可以有效解决上述问题。但是传统NSGA-Ⅱ算法的初始化种群是由一组随机生成的设计变量集合组成的，且与后代种群相同，当种群规模设置较小时，易使种群陷入局部最优解集，出现早熟现象[25]；另外，传统NSGA-Ⅱ算法在快速非支配排序后的选择过程中采用的是二元锦标赛选择策略[26]，从而造成了选择得到的交配池中一定会存在重复解，降低了种群的多样性。本文提出一种改进的NSGA-Ⅱ算法，在初始化过程中扩大初始化种群规模；搜索交配池父代种群中的重复解，并使其提前交配消除重复；改进变异算子的变异概率，使其随迭代次数增加而变小。以上改进克服了传统NSGA-Ⅱ算法的种群多样性低、易陷入局部最优解集等不足，提高了算法的搜索能力。

(1)扩大初始化种群规模

NSGA-Ⅱ算法在初始化过程中，采用随机函数，随机获取初始种群，后续再对初始种群进行快速非支配排序，从中选出较优解集[27]。初始种群规模越大，参与快速非支配排序的解也越多，找到最优解的概率也越大，但是考虑到算法的计算复杂度，初始化种群规模也不能无限扩大。为了不影响算法的计算复杂度，设置初始化种群规模为后代种群规模的两倍，使得初始化种群在经过虚拟适应度和拥挤度排序后得到的后代种群随机性更低、多样性更高。

(2)交配池去重

NSGA-Ⅱ算法在进行虚拟适应度和拥挤度计算之后，根据非支配等级和拥挤度对解进行排序，然后进入选择步骤。在选择过程中，传统NSGA-Ⅱ算法采用二元锦标赛策略，每次从排序后种群中随机选择两个解进行比较，将更优解放入交配池中。由于排序后种群数量与交配池数量相同，则在选择完成之后，交配池中一定存在重复的解，且随着算法迭代越到后期，重复解出现的概率越大，这样在一定程度上降低了算法进化过程中解的多样性。本文在选择完成后、交叉之前添加一个交配池去重步骤，找出选择完成后交配池种群中的重复解，使用模拟二进制交叉(Simulated Binary Crossover, SBX)算子对解中的整数和实数进行编码和交叉产生新的基因[28]。SBX算子的计算公式如下:

(15)

(16)

其中：βSBX为SBX算子;p1、p2为交叉父代;c1、c2为交叉子代;μ为0～1之间的随机数;γ为自定义分布指数。

改进NSGA-Ⅱ算法使用模拟二进制交叉SBX算子对选择后重复解进行交叉计算，该方法实现复杂度低，且搜索范围较小，可以适当地增加多样性的同时保护优良基因不被破坏。

(3)改进变异算子

种群的变异操作起到了局部搜索的作用，可以扩大种群的随机性[29]。传统NSGA-Ⅱ算法中使用固定的变异概率，本文提出一种变异概率随着迭代次数增加而降低的变异算子。在迭代前期，种群中的解还没有接近最优解，较大的变异概率可以增加种群的多样性，避免落入局部最优陷阱；在迭代后期，种群中的解逐渐接近最优解，变异概率变小可以保证优良基因不被破坏。算术变异概率

(17)

式中：e为当前迭代次数，emax为最大迭代次数，n为设计变量个数。

3.2 算法求解流程

改进NSGA-Ⅱ算法的求解流程如下：

步骤1初始化种群。随机生成子代种群数量2倍的解集作为初始种群，并对这些解执行目标函数。

步骤2快速非支配排序。计算初始化种群中每个个体的虚拟适应度和拥挤度。

步骤3选择交配池父代种群。使用二元锦标赛策略，从排序完成的种群中选择出较优的解集放入交配池中。

步骤4交配池父代种群去重。找出交配池父代种群中的重复解，使用SBX算子对这些重复解进行交叉，再放回交配池中。

步骤5交叉、变异生成子代种群。利用交叉算子和算术多项式变异算子对附带种群进行交叉和变异操作，得到子代种群。

步骤6精英保留。将交叉、变异前的父代种群和子代种群混合，然后进行快速非支配排序，再使用多元锦标赛策略从中选择出较优解集。

步骤7迭代。判断迭代次数是否达到最大迭代次数，已经达到则输出步骤6得到的种群作为帕累托最优解集，未达到则返回步骤3继续运行算法。

算法流程图如图9所示。

3.3 算法优越性验证

采用多目标优化测试函数ZDT系列对所提出的改进NSGA-Ⅱ算法进行测试[30]，验证改进后算法相比于传统NSGA-Ⅱ的优越性。复杂的ZDT系列测试函数为2目标模型，ZDT1的帕累托前沿为凹曲线，ZDT2的帕累托前沿为凸曲线，ZDT3的帕累托前沿为非连续曲线，ZDT4的帕累托前沿含多个局部前沿，可以测试算法解决多种不同问题的性能。

采用超体积指标HV来衡量算法的综合性能，该指标主要考虑帕累托解集的收敛性和多样性[31]。HV通过计算帕累托解集与参考点所围成的目标空间区域的体积来衡量算法的性能，HV值越大，说明算法的综合性能越好。HV的计算公式如下：

(18)

式中：δ为Lebesgue测度，用来测量体积；|S|为帕累托解集的数量；vi为参照点与解集中第i个解构成的超体积。

此外，采用多样度Δ来衡量帕累托解集在二维空间中分布的广泛程度[32]，该值越大，说明算法种群的多样性越好。Δ的计算公式如下：

(19)

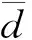
利用传统NSGA-Ⅱ算法和改进NSGA-Ⅱ算法分别运行ZDT系列多目标优化模型，设置测试函数的多目标优化种群规模为100，最大迭代次数为250次，搜索完成后得到的帕累托解集规模也是100。对得到的帕累托解集进行超体积指标HV和多样度Δ计算，得到的指标数据如表5所示。

表5 算法性能衡量指标比较

采用改进NSGA-Ⅱ算法得到的帕累托解集二维分布如图10所示。

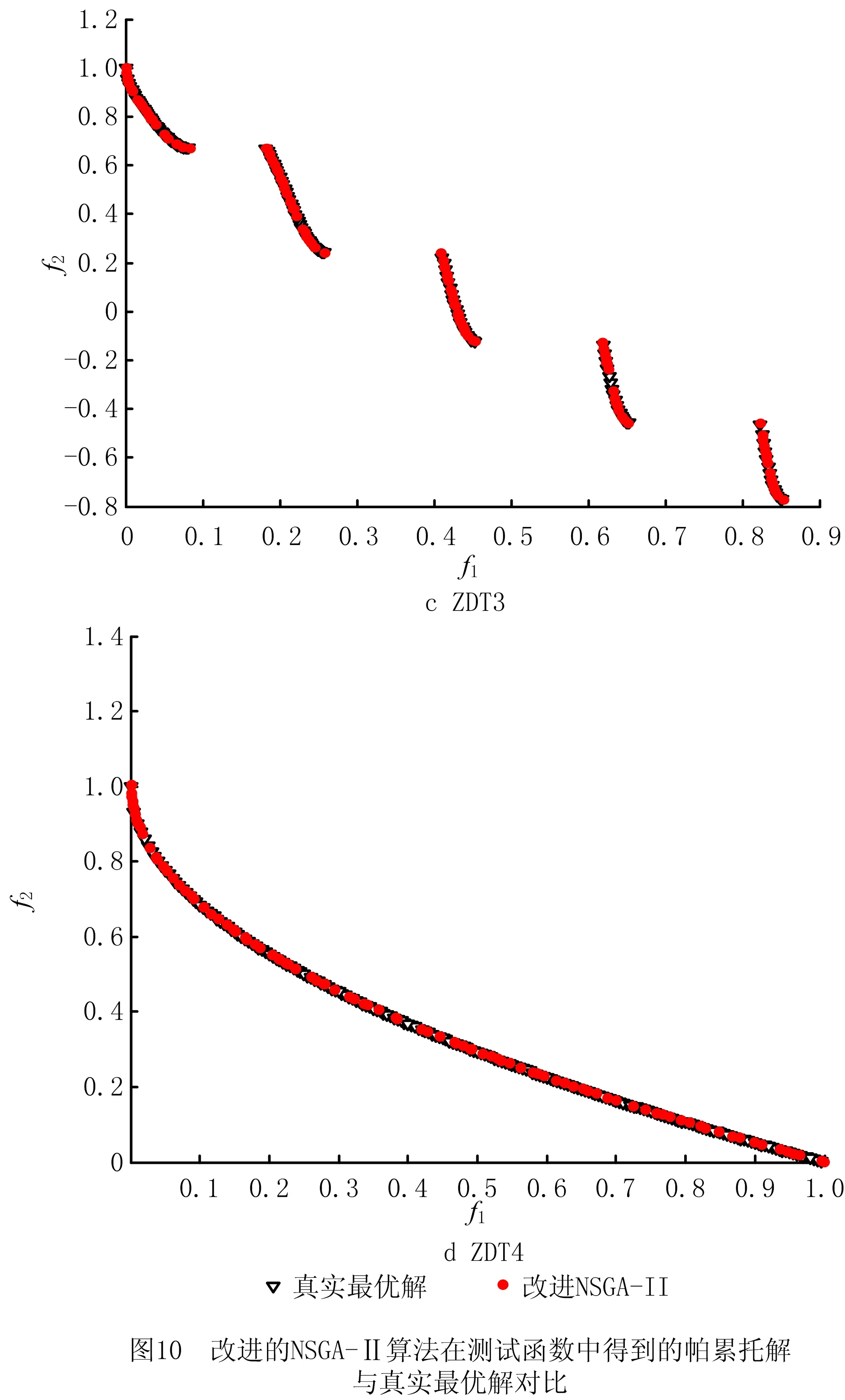
由表5可以看出，改进的NSGA-Ⅱ算法在ZDT系列多目标优化测试模型上表现出来的收敛性和多样性相较于传统NSGA-Ⅱ算法都得到了提升。通过图10可以看出，改进的NSGA-Ⅱ算法所求得的帕累托解集分布多样性优秀，且与真实帕累托前沿的重合度高。结合上述分析可得，改进NSGA-Ⅱ算法在解决多目标优化问题时，能够获得更好的帕累托最优解。

4 深沟球绝缘轴承实例分析

4.1 帕累托最优解集的分布

为了验证绝缘轴承多目标优化模型的有效性，以安装在YQ-190地铁牵引电机上的6215深沟球绝缘轴承为例，基于改进NSGA-Ⅱ算法开展以疲劳寿命、电蚀寿命和表面硬度为目标函数的优化计算，在IntelliJ IDEA平台上编程实现。该绝缘轴承的主要参数如表6所示。

表6 绝缘轴承工作基础参数

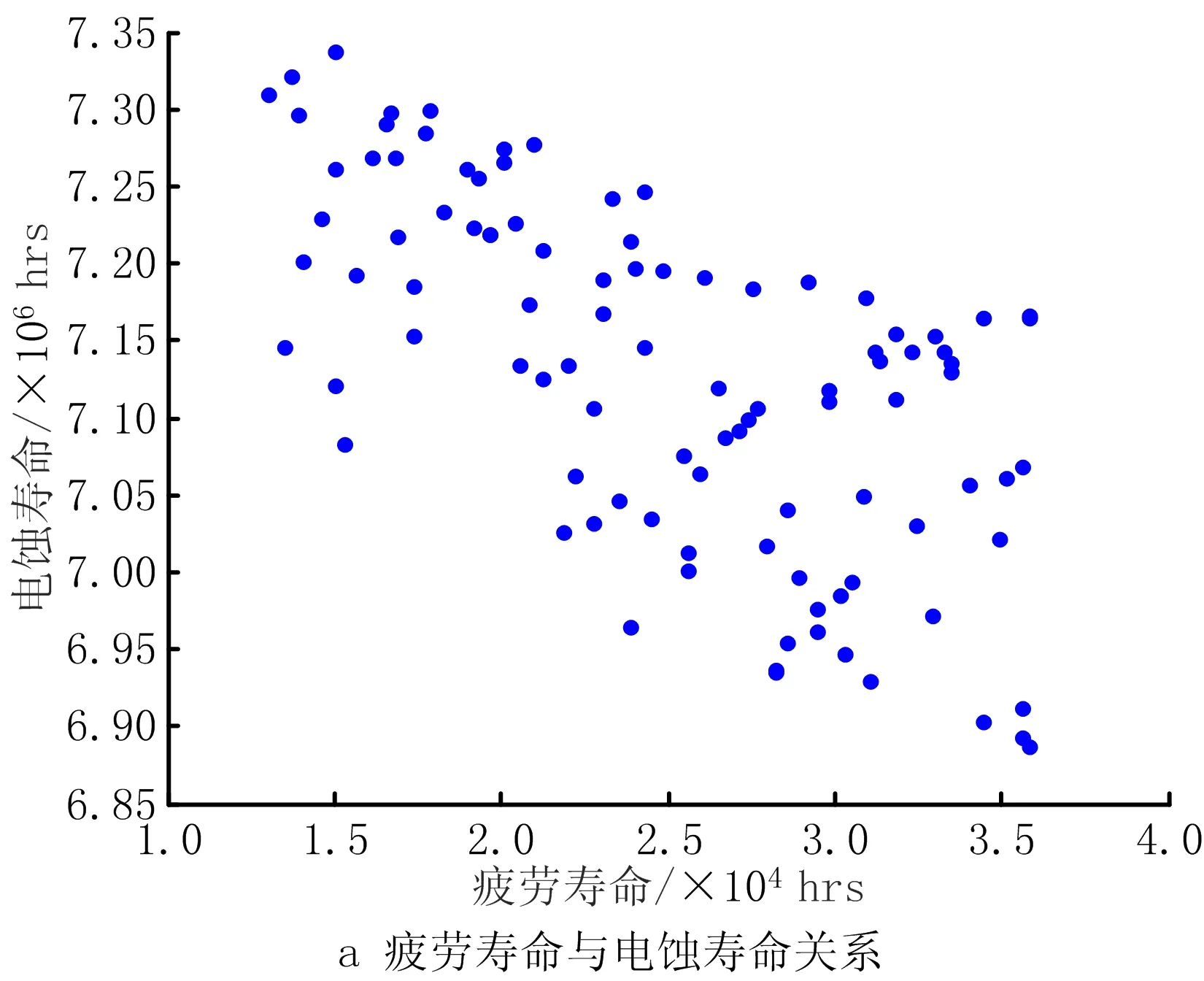
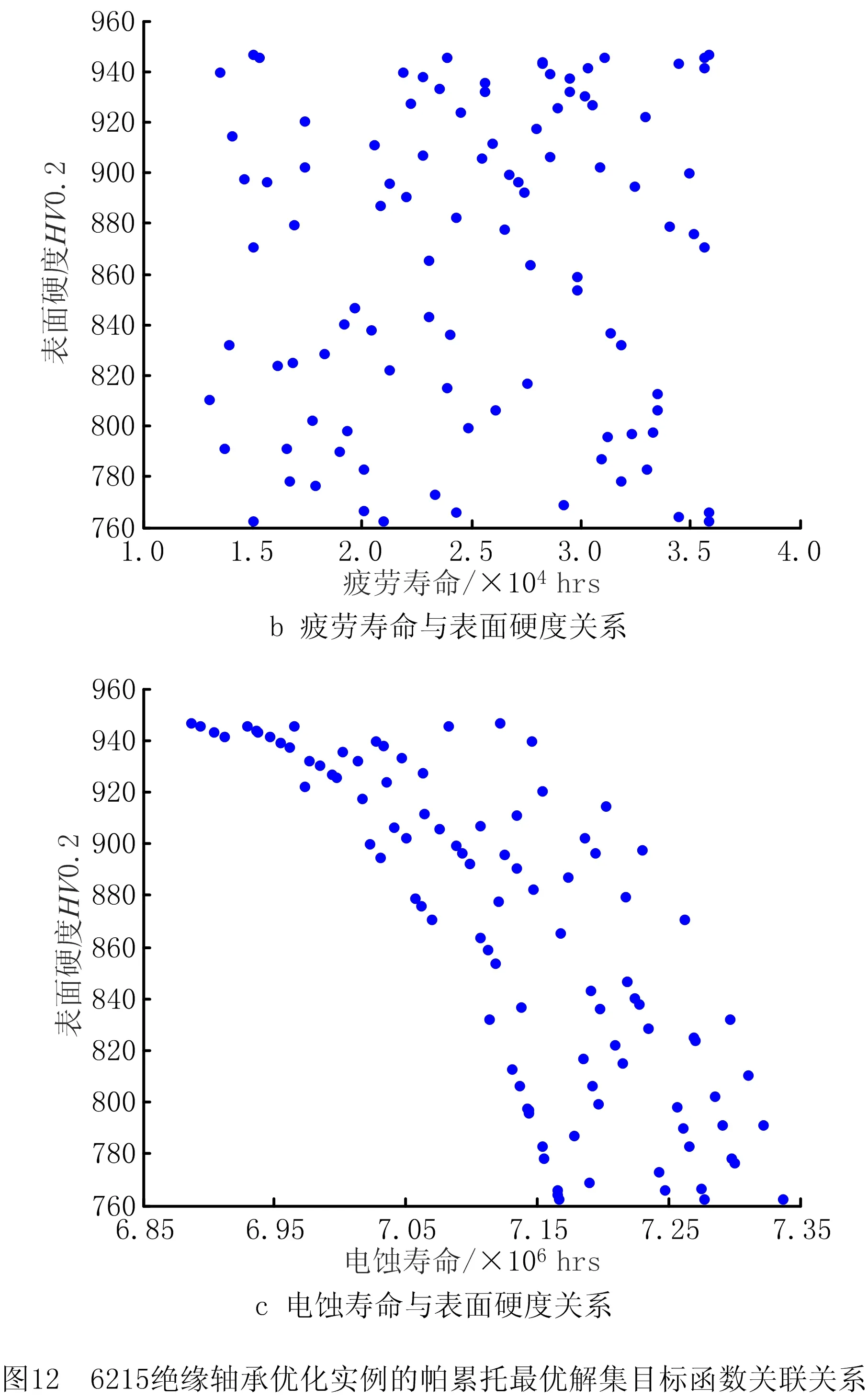
通过计算得到绝缘轴承多目标优化设计的帕累托最优解集的三维空间分布图及其拟合曲面如图11所示。从图12中可以更加直观地看出每两个目标函数之间的关系，其中疲劳寿命与电蚀寿命之间是相互制约的关系，一个目标函数的改善是以另外一个目标函数值的恶化为代价；疲劳寿命与绝缘层表面硬度之间没有明显的制约和协调关系；电蚀寿命与绝缘层表面硬度之间也是相互制约的关系，绝缘层表面硬度的增加，会导致轴承电蚀寿命降低。

4.2 优化前后分析比较

分析绝缘轴承多目标优化设计模型，可以得到绝缘层表面硬度只与设计变量中的绝缘层厚度相关，且随着绝缘层厚度减小而增大。因此，决策者在

选取最优解时，可以优先考虑绝缘层表面硬度，然后在上述表面硬度增大的前提下遵循疲劳寿命和电蚀寿命提高的原则。

遵循上述原则，选取di=600 μm,Db=17.05 mm,Dm=105.5 mm,Z=11,fi=0.515,fo=0.515。计算得到优化前后的疲劳寿命、电蚀寿命和绝缘涂层表面硬度如表7所示。可以看出，利用改进NSGA-Ⅱ算法进行优化设计得到的绝缘轴承，其性能指标相比于优化前都得到了提高，疲劳寿命提高了224%，电蚀寿命提高了1.25%，绝缘涂层表面硬度提高了4%。对于电蚀寿命来说，由于电蚀寿命公式Le=7 867 204×10-(2.17Jb)是指数函数，本文通过对绝缘轴承仿真得出EDM电流大致在0.001 A～0.002 A之间，这个区间内Jb的变化范围比较小，因此当Jb变化时，Le的变化不大，即该目标函数的优化空间本身不大。本文是对6215型绝缘轴承进行优化，在该场景下电流变化范围不大，因此电蚀寿命优化空间有限，但对于大型轴承来说，EDM电流变化范围较大，此时电蚀寿命的优化空间也会很大，因此该优化方案在工程实际中具有一定的实用价值。

表7 优化前后对比

5 结束语

变频调速电机中高速变化的电磁场与绝缘轴承相互作用，感应出的高频轴电流会对绝缘层厚度设计不当的轴承造成电蚀损伤，使其寿命低于预期，因此选取合适的绝缘层厚度等结构参数对于应用于变频调速电机的绝缘轴承至关重要。本文针对牵引电机中绝缘轴承的电蚀失效问题，提出一种绝缘轴承优化设计方法，可以改进绝缘轴承的设计参数，提升轴承的整体性能。本文主要工作包括：

(1)针对变频调速电机中的绝缘轴承电学损伤机制进行了一系列仿真分析，综合考虑了电机整体结构参数和电磁场耦合关系，得到了轴承绝缘层厚度对轴承EDM电流的影响规律模型。

(2)综合考虑影响绝缘轴承在实际工作环境中的重要性能指标，以轴承绝缘层厚度等轴承几何结构参数为优化设计变量，根据实际工作场景需要考虑设计变量约束条件，建立了绝缘轴承多目标优化设计数学模型。

(3)提出了一种用于提高深沟球轴承性能的改进NSGA-Ⅱ算法，针对传统NSGA-Ⅱ算法易陷入局部最优解的缺点，做出了扩大初始化种群、交配池去重、算术变异算子等优化，并验证了改进NSGA-Ⅱ算法的优越性。以YQ-190地铁牵引电机当中的6215绝缘轴承为工程实例进行优化设计，结果表明，优化后绝缘轴承的疲劳寿命、电蚀寿命、绝缘层表面硬度均得到有效提升。

本文在构建变频调速电机滚动轴承结构优化设计模型时将疲劳寿命与电蚀寿命分开计算，实际上疲劳损伤的主要形式是在交变剪切应力的作用下沟道表面微小裂纹的不断蔓延和扩大，而电蚀损伤的主要形式是润滑脂击穿放电导致沟道表面出现熔融小坑，则电蚀导致的小坑一定会造成疲劳裂纹的增长和蔓延加速，疲劳裂纹也一定会导致滚珠与沟道接触不均匀而加剧放电损伤现象，所以疲劳损伤与电蚀损伤之间一定存在交互作用，使得彼此加速。因此，未来可以对疲劳损伤与电蚀损伤之间的交互作用和性能退化机理作进一步的研究，同时也为绝缘轴承的设计和标准制定提供理论依据。