基于Hopfield网络的建筑物航测路径自动规划方法

钟智超 肖雄武 涂建光

(1. 武汉大学 遥感信息工程学院, 湖北 武汉 430079;2. 武汉大学 测绘遥感信息工程国家重点实验室, 湖北 武汉 430079)

0 引言

随着传感器与控制技术不断发展,无人机已经成为测绘遥感领域获取数据的重要工具[1-2]。目前常见的无人机航线规划算法致力于求解旅行客问题[3](traveling salesman problem,TSP)。常用的求解法有动态规划[4]、遗传算法、蚁群算法、概率模型估计[5]等,但这类算法很少考虑具体的飞行任务,例如，建筑物测图[6]、道路勘探、电路巡检[7]、农业植保[8]等。另外,无人机在建筑物测图领域的应用场景越来越多[9]。例如，在城市规划中,无人机结合倾斜摄影测量技术可以实现城市实景三维模型的构建;在地图生产中,无人机高精度的航片可以用于正射影像生产、数字线划图生产[10]等。

针对常见航线规划算法对建筑物测图不具备针对性的现状,提出一种针对建筑物测图的无人机航线自动规划算法。针对建筑物与植被粘连的问题,结合影像的光谱特性分离植被,缩小作业范围;设计基于无人机多视图立体几何的地表地势的估计方法,分析出飞行区域内粗略的高区和低区;结合植被信息与地势信息完成对建筑物区域的分割;设计基于边缘检测的建筑物主方向识别,优化航线角度;最后利用霍普菲尔德网络求解覆盖多个建筑物区域的最优路径。

1 测区内建筑物区域定位

建筑物测图任务中,研究对象是建筑物，不包含其他地物。而常规的无人机规划线路往往对整个测区进行“条带状”的航带划分,如图1所示,这会导致大量的无用航点和无用航片,尤其是在建筑物集群分布而且群体之间的距离较远的情况。

图1 “条带状”航线和常见“无效航片”示例

1.1 植被区域分离

植被是建筑物测图中“无效航片”的重要来源,建筑物集群分布的特性导致存在大量仅被植被覆盖的区域,可以利用植被特有的光谱特性来区分其与别的地物类型,如式(1)所示。

(1)

式中,(x,y)为像素;NIR(x,y)为近红外波段值;R(x,y)为红色波段的灰度值。归一化植被系数(normalized differential vegetation index,NDVI)可以用于区分常见的绿色植物。绿色植物对近红外波段的反射率较高,对可见光红色波段的吸收率较高,因此将NDVI(x,y)大于阈值的像素标记为植被。

1.2 地表地势估计

除了植被之外,“裸地”也是非建筑物地物中占地面积较大的部分,尤其对比较干旱的测区,“裸地”的影响程度更大。区分建筑物与“裸地”的重要方式是通过地势高低差来判断。在无人机作业中,很难直接获取精确的地势高程数据,如数字表面模型(digital surface model,DSM)等,因此可依靠无人机多视角测量来估计地表[11]。

1.2.1无人机多视立体几何

第一步,利用无人机在起飞点附近俯拍整个测区(根据测区大小调整飞行高度),记录拍照瞬间无人机传感器的位姿信息,具体包括外参矩阵R1以及根据全球定位系统(global positioning system,GPS)定位获取的摄影中心初始位置信息,用矩阵t1表示。值得注意的是,初始时姿态角可以直接利用无人机万向角信息进行初始化。

第二步,移动无人机并调整镜头位姿,在另一位置拍摄,同样覆盖整体测区。其间通过无人机惯导数据结合初始化的位姿推算第二次拍摄瞬间的位姿R2和t2。

第三步,根据灰度特征匹配两张影像,计算出匹配点对的深度,从而获取对应3D点的估计坐标。

图2中,地表上不同地物同时被两次拍摄记录到,对于地表的一点P(X,Y,Z),其对应两张影像上的两个像素点p1(u1,v1)和p2(u2,v2),在已知两次摄影无人机位姿的估计值,那么有式(2)的关系。

(2)

式中,K为相机的内参矩阵，由于未知量是地表点P(X,Y,Z)坐标,因此至少需要两组同名点对才能求解该问题,因此需要无人机在不同的位姿对同一地表进行拍摄。

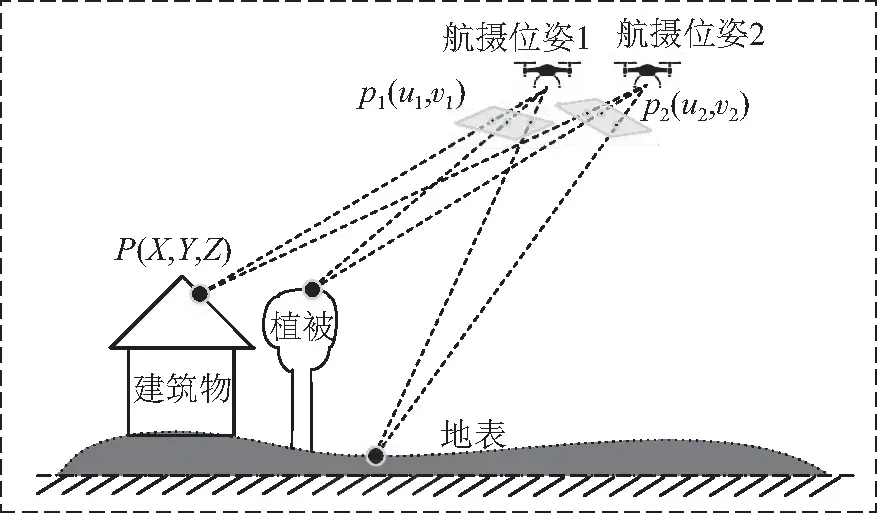
图2 利用无人机多视立体几何估算地表示意图

1.2.2估计地形表面

通过无人机多视立体几何可以求解地面点的三维坐标[12],因为位姿不够精确,所以这种方式求解的地面点是不够精确的。但是这一步只需要对地表地势有一个相对估计,即能够区分地表上哪些位置地势更高(如建筑物、树木等),哪些位置地势更低(如裸地、坑洼等)[13],因为地表本身是有坡度的,首先需要对地表面进行拟合。建筑物或树木产生的高度差是突变的,而地表面是缓慢地升高或降低,因此可以设定一个权重函数限制这种突变,如Kraus和Pfeifer提出的分段式权重函数,如图3所示,根据高度变化残差的大小来重新加权计算高程[14]。

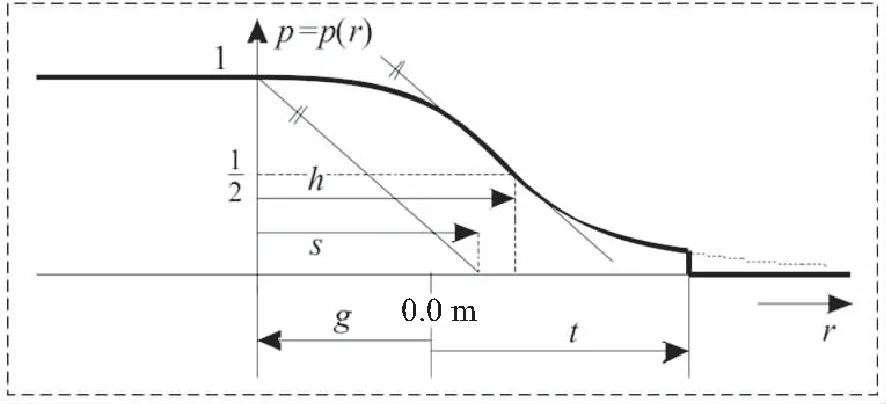
图3 用于估计地形表面的权重函数

图3中,p(r)为权重关于残差变化的函数;r为残差大小;g和t为分段权重的残差阈值。首先用等权重来加权这些点的坐标Z值,拟合一个初始的地表面,然后逐点比较坐标Z值与拟合表面的估计值的差异,根据差异的大小来重新加权Z值。该分段权重函数把残差大于阈值t的点直接设置为“外点”,权重设置为0。

把分段拟合后的地表面记为GS,那么区分某点P(X,Y,Z)是否属于建筑物的方法如式(3)所示。其中(x,y)表示与点P(X,Y,Z)对应的像素坐标。

(3)

2 单区域航线规划与全局最优求解

2.1 单区域航线规划

边缘特征描述了像素之间的梯度关系。数学上,用一阶导数来表达像素梯度被称为一阶微分算子,如Sobel算子、Canny算子等。利用二阶导数来检测梯度的算子被称为二阶微分算子,如LoG算子等。为了提高建筑物边界检测结果的完整性,防止出现对不明显的边界的漏检,设计了一种8方向的增强一阶微分算子,算子的结构如图4所示。该算子对比普通的一阶算子的改进包括,第一,从普通一阶算子只检测2个方向的梯度变化,拓展到检测8个方向;第二,扩大了检测算子的邻域大小,从3×3拓展到5×5,增大梯度检测的感知范围。

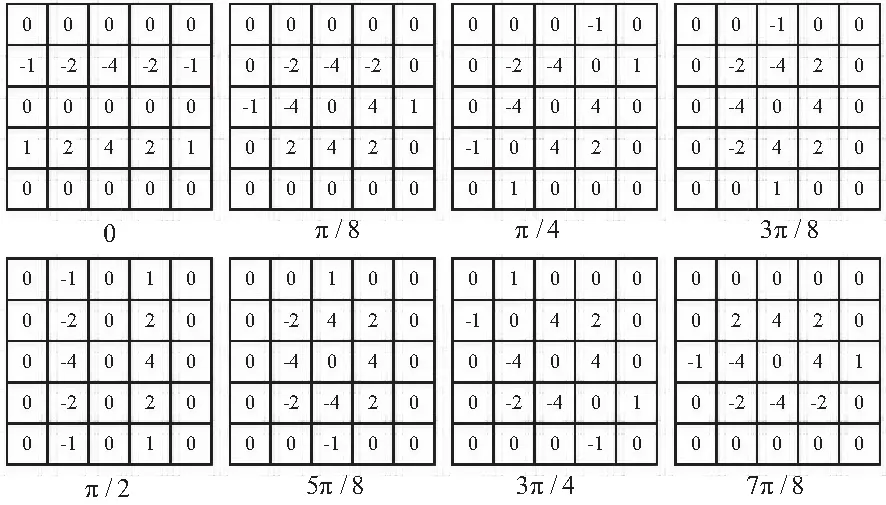
图4 8方向增强边缘检测算子

为了验证该改进算子的提取能力,设计了与经典的Canny算子、LoG算子的对比实验,验证结果如图5所示。可以看出,虚线框中目标建筑物被阴影遮挡的边缘梯度很小,提取难度较大,该8方向增强算子能保持较好的检出率。

图5 8方向增强算子提取建筑物边缘的对比结果

建筑物的主方向可以表示该建筑物的朝向,假设用方向向量d表示主方向,首先利用Hough变换对2.1中获取的建筑物边缘进行线段化,得到所有表示建筑物边界的直线段集合L。根据直线段判断建筑物区域的主方向步骤如下,如图6所示。

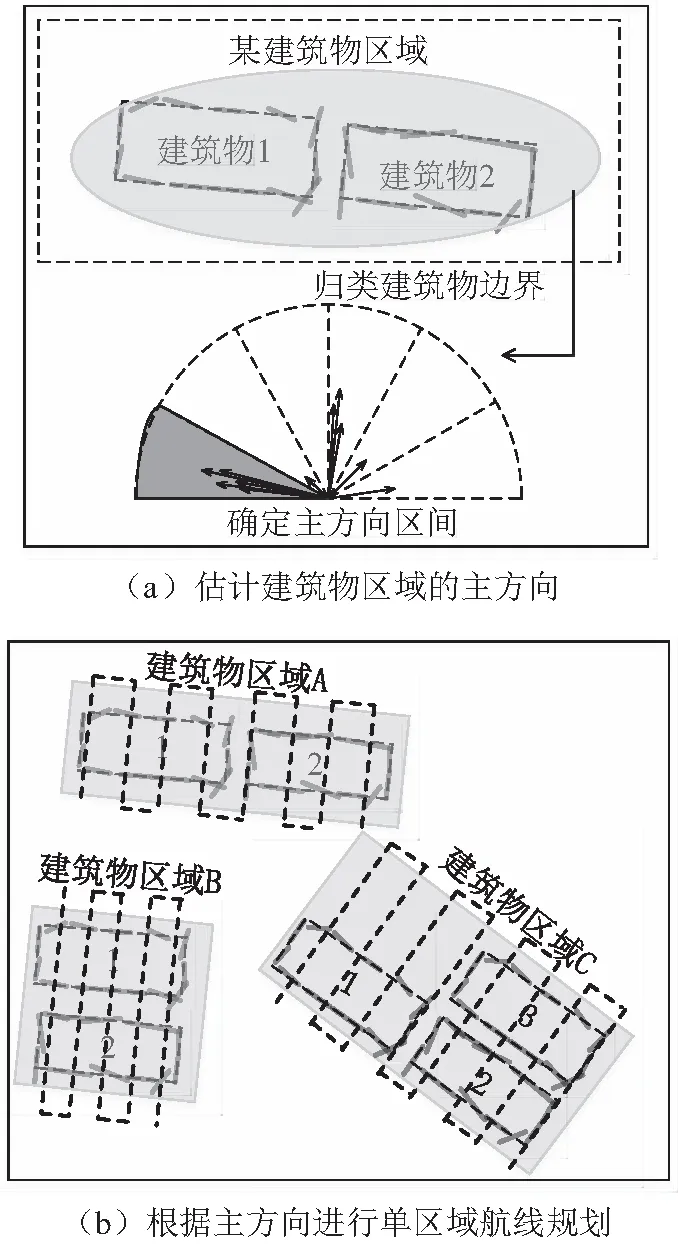
图6 确定主方向与单区域航线规划

第1步,对于任意L中的每一条直线段,先计算其长度,对于长度小于阈值(根据经验一般设定为真实尺寸1.5 m)的设定为噪声,对于长度大于阈值的保留为有效线段。

第2步,对于每一条有效线段,计算其方向向量。按照每30度为一个区间划分6个方向角区间,根据方向向量将这些有效线段分到这6个区间内。

第3步,统计每个区间内有效线段的总长度,挑选出总长度最长的一个区间,将区间内的所有线段的方向向量按照长度进行加权求和,得到该区域内建筑物的主方向。

2.2 全局最优航线求解

无人机的单次任务是从起飞到降落的全过程,需在尽可能短的时间内,完成对所有建筑物区域的飞行任务,即找到从起飞点到完成所有建筑物拍摄并返回起飞点的最短路径。Hopfield神经网络是一种结合存储系统和二元系统的神经网络。基于连续Hopfield的特点,如果把一个最优化问题的目标函数转换成网络的能量函数,把问题的变量对应于网络的状态,那么Hopfield神经网络就能够用于解决优化组合问题[15]。

2.2.1能量函数构建

首先构建无人机飞行的Hopfield次序矩阵e,次序矩阵中的元素eij代表无人机在第i时刻执行j建筑物区域的飞行任务。假设所有的目标建筑物区域总数为N,那么将产生如下约束条件。约束1,次序矩阵的每一行只有一个神经元被激活,即每个区域有且只有1次飞行任务;约束2,次序矩阵的每一列只有一个神经元被激活,即无人机不能同时执行2个或2个以上区域的任务;约束3,次序矩阵所有激活的神经元数量之和等于所有的建筑物区域数量总和,即无人机需要执行完所有建筑物区域的飞行任务。三个约束条件如式(4)所示。

(4)

无人机整体测区路径优化的目标是所有路径长度加起来最小,如式(5)所示,其中d表示距离矩阵,dik代表第i个飞行区域到第k个飞行区域的距离,默认在初始时对这些待飞区域进行了编号。

(5)

因此,将三个约束条件以及最小化总路径长度的目标函数转化为能量函数的惩罚项,可以得到总体能量函数的表达式，如式(6)所示。

(6)

式中,前3项是约束项；第4项为目标函数；A、B、C、D为惩罚参数,为固定值,这些值反映了这几项在最小化过程中的相对重要性。

然后将式(6)描述的航线优化问题按照Hopfield网络标准能量函数对应起来,其标准形式如式(7)所示。

(7)

式中,权重和偏重Wijkl、Iij展开表示如式(8)所示。

(8)

式中,δij代表指示函数,其在i=j时取值为1,i≠j时取值为0。

2.2.2迭代求解最优航线

确定航线优化问题的约束条件和标准能量函数之后,需要不断迭代修正权重矩阵,直到状态趋于稳定,具体的步骤如下。

第1步,设定惩罚系数A、B、C、D和最大迭代次数Tmax,随机初始化次序矩阵e。

第2步,计算各个建筑物区域之间的距离,形成距离矩阵d。

第3步,根据初始化的输入状态U0,确定状态转移函数,如式(9)所示。

(9)

第4步,计算输入状态的增量,如式(10)所示。

(10)

第5步,利用动态方程和一阶欧拉法更新下一刻的输入状态和输出状态,如式(11)所示。

(11)

第6步,检查当前的输出状态e是否满足约束,判断迭代是否结束,否则返回第4步,直到迭代次数达到设定的最大次数。

3 实验分析

为了验证该航线规划算法的有效性,利用国际摄影测量与遥感学会(International Society for Photogrammetry and Remote Sensing,ISPRS)提供的公开数据进行模拟实验,该地区的建筑物占地面为4 099.5 m2。该地区建筑物面积较大,分散分布且树木环绕,首先对其中的建筑物区域进行定位,结果如图7所示。

图7 建筑物区域定位实验结果

如图7(a)所示,目标测区内建筑物分散分布且在朝向上具有明显差异;图7(b)中亮区代表植被,暗区代表非植被;图7(c)中亮区代表地势高的区域,暗区代表低地势;结合图7(b)和图7(c)可以定位具体的建筑物区域,利用增强8方向的检测算子提取目标建筑物的边界,如图7(d)所示。

根据建筑物区域的定位结果与边缘提取的结果,然后计算每个区域内建筑物的主方向,根据主方向确定每个小区域内的航线。最后将所有小区域的航线全部生成后,通过全局航线优化确定无人机执行各区域飞行任务的顺序。在初始化Hopfield距离矩阵时需考虑到建筑物区域本身具有的空间宽度,距离是两个区域最小外接矩形几何中心之间的距离。确定初始距离矩阵之后,设置初始系数A=B=D=50,C=20进行Hopfield网络的迭代趋近,结果如图8(b)所示,输出状态在迭代20次左右逐渐稳定,最小损失稳定在315.654,并得到如图8(a)所示的整体航线优化结果。

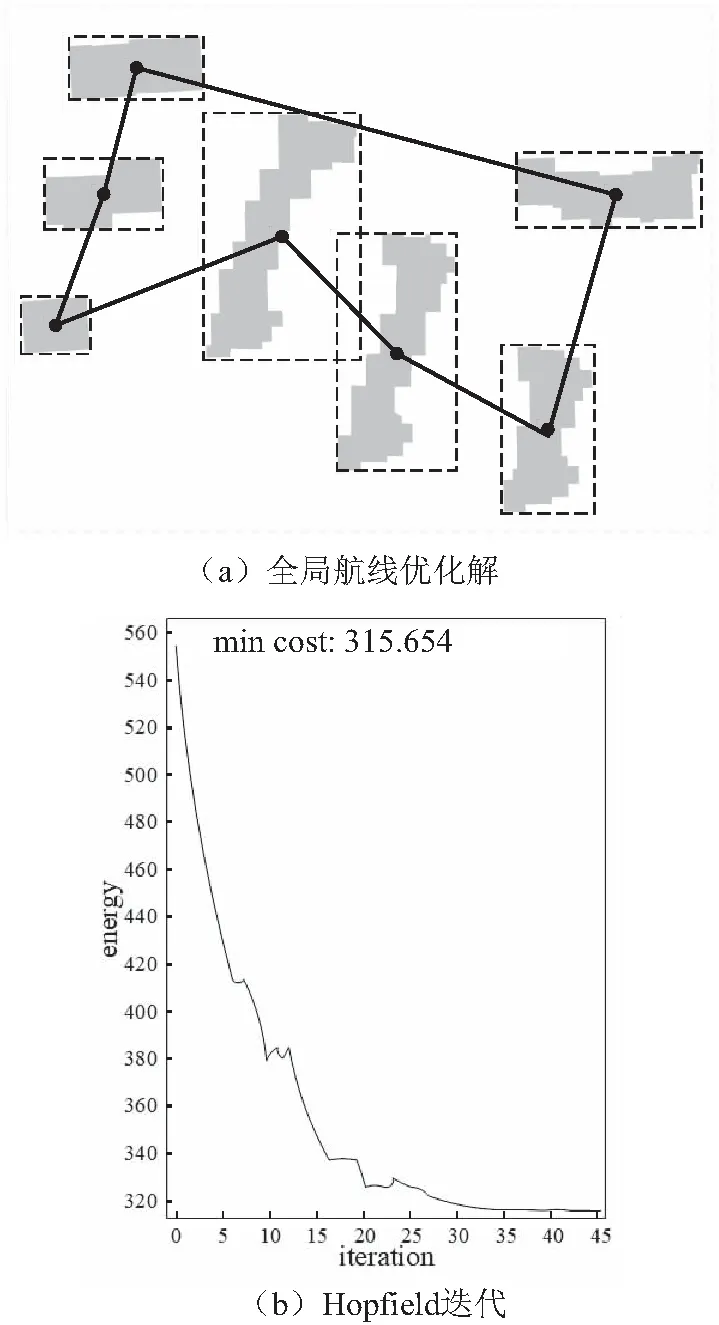
图8 全局航线优化结果与Hopfield网络迭代收敛

为了验证该方法规划的航线与不考虑建筑物分布的“条带状”航线的效率差异,设计了同区域的对比实验。设置相同的重叠率使得航带间距为12 m,固定无人机飞行速度为6 m/s,忽略无人机拍照时间与等待,生成的航线结果如图9所示。为了合理地评价无人机执行飞行任务的效率,这里给出一些指标。

有效航线距离(d1)：属于航线规划的航线,在建筑物区域(参考图8(a)所示的建筑物区域定义)内的航线长度。

通勤距离(d2)：从当前航线飞往下一航线的中间过程飞行距离。

无效航线距离(d3)：属于航线规划的航线,但是不属于建筑物区域内部,在无效航线上拍摄的航片称为无效航片。

航线效率(r1)：有效航线距离与航线规划的总长度的比值(不包括通勤距离)。

作业效率(r2)：有效航线距离与无人机作业全流程飞行总距离的比值(包括通勤距离)。

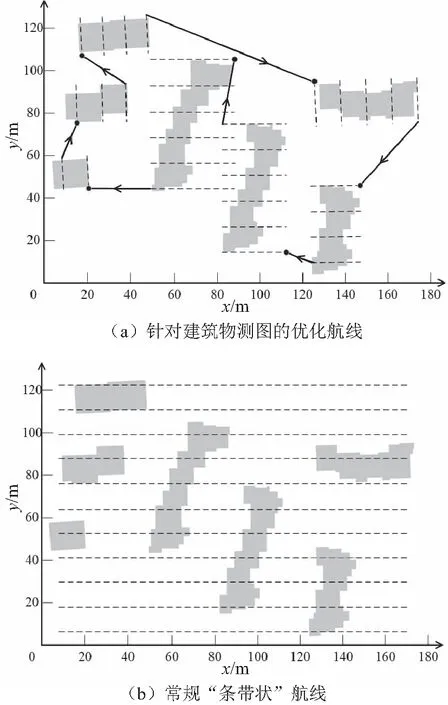
图9 两种方法生成的航线结果

根据模拟实验数据得到如表1所示的实验结果,可以看出,常规“条带状”航线的总飞行距离为3 447.6 m,本文方法总飞行距离为1 090.6 m,相比“条带状”航线缩减了2 357 m,降幅在68.4%左右。从具体指标来看,针对本文方法的航线效率为91.2%,“条带状”航线为38.5%。整体的作业效率方面,本文方法作业效率为71%,传统方法为20.3%。实验结果表明,在建筑物测图类型的任务中,本文方法可以明显提高无人机的作业效率,降低工作时间,同时保证航片质量。

表1 两种航线规划算法对比结果

4 结束语

本文提出了一种针对建筑物测图的无人机全自动航线规划方法,首先利用NDVI结果分离区域内的植被;再利用多视立体几何方法粗略估计地表地势,计算出建筑物区域的位置;并提出了一种增强8方向的边缘检测算子来估计建筑物的主方向,调整航向角度;最后利用Hopfield网络迭代求解全局的最佳飞行顺序,得到完整航线。实验表明,对于建筑物航测,该方法比“条带状”航线在飞行距离上减少了68.4%,总作业效率提高了50.7%。