基于改进自组织神经网络的创业数据评估建模与仿真

尹诗

（上海第二工业大学，上海 201209）

随着社会经济的不断发展，学校和国家为毕业生就业提供了众多资源，例如大力支持自主创业、提供政策扶持等，这使得越来越多的高校毕业生在毕业时会选择自主创业。但目前高校对创业数据的分析匮乏，故无法对学生进行积极引导，而现有的一些算法模型也存在准确性及预测稳定性较差等问题[1]。因此为了更优地推进大学生自主创业水准、提高高校创业数据分析能力，文中基于改进自组织神经网络技术提出了一种创业数据评估模型与仿真方法。该建模方法通过SOFM 算法对数据做出选择与分类，并利用Duplex算法对数据集的划分、回归模型及共识模型的建立等过程进行了创业数据的建模与仿真，仿真结果充分体现了所提方法在进行创业数据建模时的优势，同时还验证了该方法的可靠性与有效性，并为高校进一步分析创业数据提供了重要参考。

1 自组织神经网络

1.1 基本原理

自组织神经网络（Self-Organizing Map,SOM）是人工智能领域神经网络技术的一个重要分支，本质上是一种基于无监督机器学习的自组织竞争网络，其基本思想是Rosenblatt 根据人脑神经元自组织、自适应的特征而提出的[2]。SOM 模型是对研究对象的拓扑分析，即将研究对象抽象成高维空间向低维空间的非线性映射，同时不改变研究对象的拓扑结构，使得原本在高维空间抽象的拓扑结构在低维空间以可视化的方式展示出来。SOM 模型能够在无人为干预的条件下，通过自主学习与训练不断改变和优化网络模型中涉及的相关参数，并可对输入对象进行有效分类。目前，其经常被使用在分类聚类、模式识别、组合优化及数据压缩等领域中。

典型自组织神经网路SOM的网络结构如图1所示。

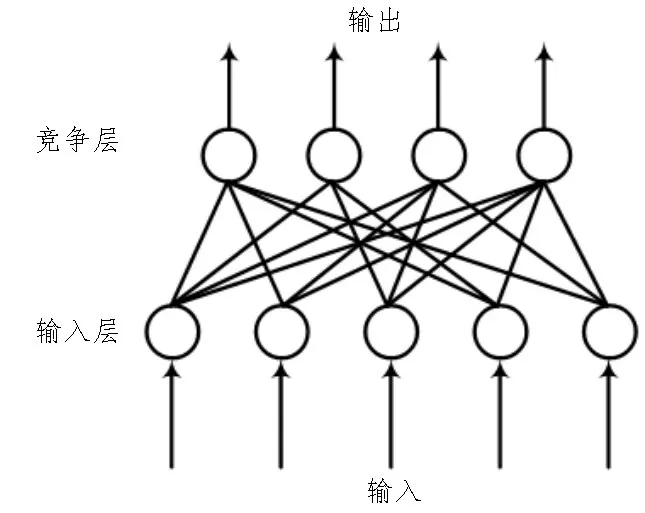
图1 典型自组织神经网路SOM的网络结构

由图1 可知，SOM 网络结构主要由输入层和竞争层（输出层）两部分神经元组构成[3]。其中，输入层用来接收输入对象对应向量，向量的各个元素分别存储于输入层不同的神经元之中，这些神经元与竞争层神经元相连，并通过二者之间的连接渠道将对应元素的数据传递给竞争层。竞争层利用这些数据构建不同的判别函数，再根据某种规则对各判别函数的值进行对比，从而选择其中的最优解，同时根据得到的最优解进行反推，进而可以不断调整网络模型的输入参数。

竞争层包含一个重要的过程——竞争学习，其主要作用在于使竞争层的各节点进行竞争，且当某一节点取胜后（依赖判别函数），按照该节点的相关属性对模型参数进行调整。当神经网络中输入相似的研究对象时，该节点更容易取胜，从而完成模型的竞争学习。竞争学习主要包括以下3 个环节[4]。

1）竞争：竞争层中每个神经元与输入层神经元之间的连接权值构成对应的判别函数。当输入对象为自变量时，计算判断函数所对应的因变量值，并选择这些值中的最优解对应的神经元为该次自适应竞争学习的最佳匹配神经元。

2）合作：最佳匹配神经元与周围其他神经元进行合作，共同进行模型的自适应学习，同时其也成为所需调整的神经元[5]。

3）自适应：最佳匹配神经元拓扑邻域中所有的神经元需要根据输入对象不断调整输入层与竞争层之间的连接权值，以此改变这些神经元所组成的判别函数，进而对模型的输入参数进行优化。

1.2 改进自组织神经网络

SOM 模型的优势在于具有自适应性，在进行非线性映射的同时能够保证输入对象的拓扑结构不发生改变，但其缺点也较为明显，例如网络模型在训练时有些节点可能始终无法取胜，使得网络出现死神经元，并造成资源浪费。此外，若要给SOM 网络增加新的训练类别，则必须重新进行完整的学习，综合扩展性能较弱[6]。

针对上述传统SOM 算法模型存在的问题，国内外学者均提出了多种不同的改进方案，其中被大家熟知且应用最为广泛的是芬兰学者Kohonen 建立的自组织特征映射神经网络（Self-Organizing Feature Map，SOFM）模型。该模型相对于传统SOM 模型除了能够解决上述问题外，其思想更为完整且算法处理效果更优[7]。SOFM 模型在架构上与传统SOM 模型相似，均是由输入层与竞争层组成，不同的是SOFM模型的竞争层优化成了全互连的神经元整列，其对应的拓扑网络架构如图2 所示。

图2 SOFM网络结构

SOFM 模型的输入层与SOM 相同，均为输入对象对应向量各元素神经元的集合；而竞争层则是由n×n个神经元所组成的二维全互连阵列。SOFM 模型将高维对象对应的向量映射到二维平面上，且在网络训练过程中将输入向量的维度固定为所设置的初始值m。该m个神经元与二维竞争层上的神经元通过连接权值进行连接。竞争层中根据不断的竞争学习使SOFM 模型的训练结果朝着最有利方向反复优化。最终，得到唯一的最佳匹配神经元[8]。在训练过程中，网络模型会不断地加强取胜的神经元和处于取胜神经元邻域的神经元，同时对其他的神经元进行抑制[9]。其示意图如图3 所示。

图3 模型竞争层训练示意图

其中，二维竞争层上的神经元均有与之对应的正负号，代表着该神经元在此次训练中是被加强或是被抑制（“+”代表加强，“-”代表抑制）。

2 数据建模

文中研究的目的是基于改进自组织神经网络模型对创业数据进行建模与仿真，进而实现创业数据智能评估。其数据建模过程如图4 所示。

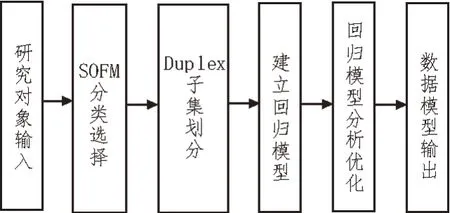
图4 基于改进自组织神经网络模型的数据建模过程

上述过程可描述为：首先通过自组织特征映射神经网络SOFM 模型对研究对象的特征变量进行选择与分类，使具有相似性的变量产生聚集，同时在其中选择若干子集进行后续处理；然后利用Duplex算法将数据子集划分为训练集、验证集、测试集，再根据训练集建立回归分析模型[10]；随后利用验证集对各模型的预测结果进行分析，并选择其中的最优模型计算对应的误差；最后根据得到的误差计算最终共识模型各部分的权重，并利用加权的方法将预测集的结果进行组合，形成最后的共识作为评估结果[11]。

2.1 SOFM分类聚类过程

SOFM 模型应用于分类聚类领域的算法流程如图5 所示。聚类中常用相似度作为必要条件，把相似度高的元素聚集在一类，相似度低的元素则处于不同的类[12]。文中在设计时，用欧氏距离表示相似度。

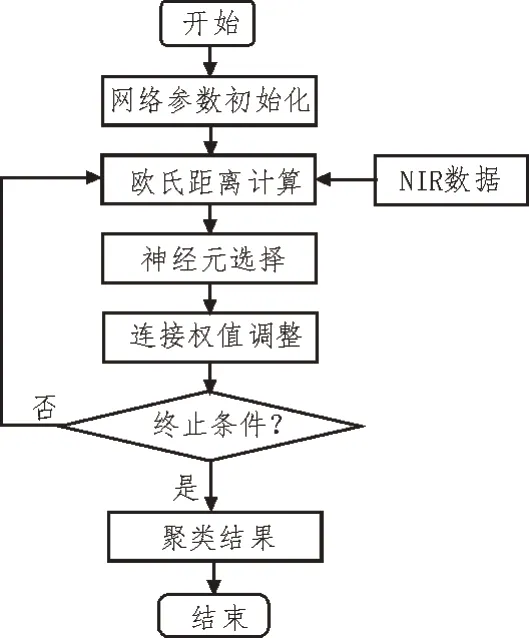
图5 SOFM算法流程

具体步骤为：

1）SOFM 模型各参数初始化，同时将连接权值设置为随机值；

2）利用欧氏距离计算输入层向量与竞争层神经元之间的距离；

3）选择欧氏距离最优解对应的神经元作为最佳匹配神经元；

4）根据最佳匹配神经元调整步骤1）中的连接权值；

5）判断是否满足终止条件，若满足，则输出聚类结果，流程结束；若不满足，则跳转至步骤2），流程继续。

2.2 建立回归模型

目前常用的回归模型分为两大类[13]：线性算法和非线性算法。其中线性算法包括最小二乘法（LSM）、多元线性回归等；而非线性算法则包括BP 神经网络、SVM 算法等。文中在考虑实际建模需求的情况下选用最小二乘法，即LSM 算法。该算法是统计学中的一种经典算法，也被称为最小平方法，其数学模型可简单描述如下[14]：

y=Xb+c（1）

式中，y为响应变量，X为对数据采样所得到的样本矩阵，b为回归向量，c为偏差因子。

2.3 建立共识模型

共识模型的构建可分为两部分：1）选择适合的建模方法，训练多个相互独立的子模型；2）采用某种共识规则将上述模型进行组合，并得到最终的共识结果[15-16]。为了使共识模型更加准确，在训练子模型时，要使最终的子模型具有一定的预测能力且互不关联。而在对子模型进行组合时，也要采用最优的关联规则。建立共识模型的主要目的在于单个子模型所涉及的面相对较窄，而共识模型能在多个纬度上对数据的信息进行分析，同时还可降低噪声等无关因素的影响。为此，文中建立了基于SOFM 的共识模型，如图6 所示。

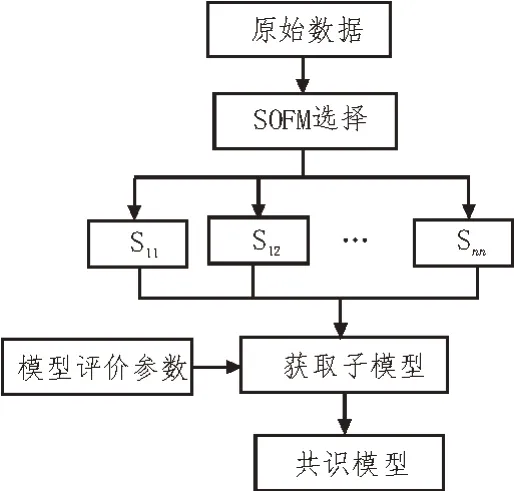
图6 基于SOFM的共识模型

该模型的工作流程可描述为：

1）原始数据通过SOFM 模型选择若干数据子集；

2）对每个样本子集利用LSM 和BP 神经网络训练相应的子模型；

3）利用模型评价参数对子模型进行评价，并选择各数据子集中最优的子模型；

4）通过共识规则将子模型进行组合，得到最终的共识模型。

3 仿真测试

为了验证文中基于改进自组织神经网络的创业数据评估建模方法的有效性与可靠性，采用某高校近十年的创新创业原始数据集对所提出的建模仿真方法进行测试。

3.1 硬件配置

建模仿真实验的硬件条件具体如表1 所示。

表1 建模仿真硬件条件

3.2 数据建模仿真

在上述硬件条件下，将原始数据集分为8 组，为了体现所提建模算法的优势，分别利用文中方法和文献[16]中的方法进行建模，同时利用预测均方根误差（RMSE）和标准差（SD）作为判别模型的标准。均方根误差（RMSE）的值越小，模型的表现效果越优；标准差（SD）的值越小，则对数据的预测越稳定。两种方法的建模结果分别如表2 和表3 所示。

表2 文中方法建模结果

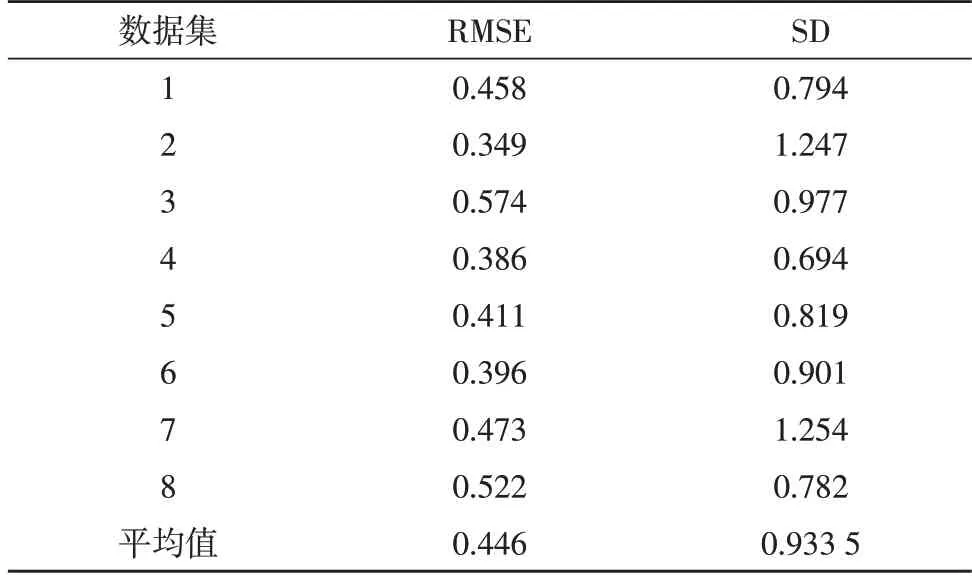
表3 文献[16]方法建模结果

由以上两个表格的结果可以看出，文中建模方法的均方根误差（RMSE）和标准差（SD）均小于文献[16]中的建模方法，充分说明所提方法在模型准确性和预测稳定性上均优于对比方法；同时该项测试验证了文中所提方法的可行性与可靠性，并能够为准确地进行创业数据建模与仿真提供了重要参考。

4 结束语

文中基于改进自组织神经网络算法，提出了一种创业数据评估建模方法。该方法由SOFM 算法模块、Duplex 算法模块、回归模型模块和共识模块4 部分组成，各部分相互配合共同完成创业数据的建模与仿真。为了验证所提建模方法的有效性，文中设计了一组对照实验，并以均方根误差（RMSE）和标准差（SD）作为判别标准参数。测试结果说明，文中方法在模型准确性和预测稳定性上均优于对比方法，验证了所提方法在数据建模中的可行性。