基于数字滤波和相位补偿的舰船升沉测量方法*
2022-10-11李宏生刘锡祥张玉鹏赵苗苗
沈 航, 李宏生, 刘锡祥, 张玉鹏, 赵苗苗
(1.东南大学 仪器科学与工程学院,江苏 南京 210096; 2.微惯性仪表与先进导航技术教育部重点实验室,江苏 南京 210096)
0 引 言
舰船在进行海上作业时处于复杂的海洋环境中,会产生六自由度的摇荡运动。其中,沿着半固定坐标系垂向轴的升沉运动对舰船系统性能的影响和危害最大。能否实时、精确地获取垂向轴的速度和升沉信息对舰载武器的发射、舰载机的起降意义重大[1,2]。
现有的基于惯性测量和数字滤波的组合测量方法通过安装在舰船上的惯性测量单元(inertial measurement unit,IMU)实时敏感垂向综合加速度,再经过两次积分与数字滤波后得到升沉信息。然而传统数字滤波器会固有地改变输入信号的幅频、相频特性,造成幅值衰减和相位偏移,对升沉测量的精度产生较大影响[3,4]。
针对IIR数字高通滤波器输出信号相对于实际信号相位超前、幅值衰减的问题,提出了一种新的升沉测量方法,在最大程度地滤除低频干扰的基础上,分别对高通数字滤波后的速度和位移使用带限傅里叶线性组合(bandlimited multiple Fourier linear combiner,BMFLC)算法进行幅值和相位补偿,得到较高精度的垂向速度和升沉位移。最后通过仿真与转台试验验证了上述方法的有效性。
1 基于捷联惯导系统的升沉运动测量
根据捷联惯导系统(strap-down inertial navigation system,SINS)的比力方程,取地理坐标系为导航坐标系(n系),并将地理坐标系的信息转换至升沉所在的半固定坐标系(s系)。具体公式如下
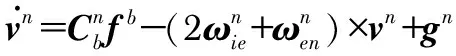
(1)
(2)
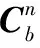
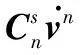
2 BMFLC算法原理
通常,升沉运动的频率在整个升沉频段内实时变化,需要找到一种方法对实际的垂向速度和升沉位移进行实时的拟合。Veluvolu K C等人提出的BMFLC算法以整个通频带为基础进行拟合,尽管只用了一次谐波分量,但是充分使用了通频带内的多个频率,使算法在通频带内的拟合效率得到了很大提高[8]。
BMFLC算法根据使用的要求预先设置频段范围为f1~fN,并以Δf为步长,将整个频段等间隔划分成N-1段,总共有N个频点,fr=f1+(r-1)Δf,1≤r≤N。
舰船的升沉运动在短期内可视作是一种准周期运动,可以用正、余弦形式来表达
(3)
采用LMS算法对式(3)中的权重系数ark,brk进行实时调整,从而达到对未知输入信号进行实时估计的目的。
BMFLC算法示意如图1所示。
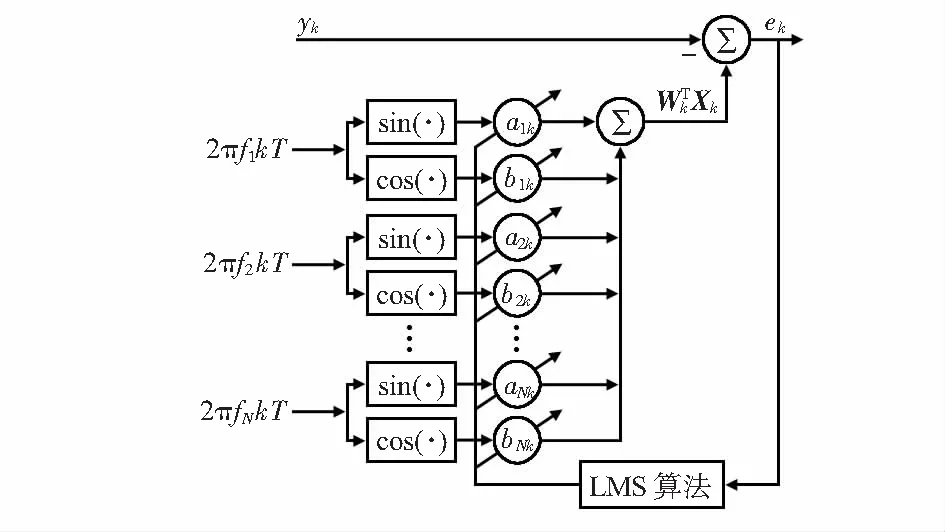
图1 BMFLC算法示意
相应的递归形式为
(4)
(5)
Wk+1=Wk+2μεkXk
(6)
式中Wk=[a1k,…,aNk,b1k,…,bNk]T为所有拟合频点组成的权重系数向量;Xk=[x1k,…,xNk,xN+1k,…,x2Nk]T为所有拟合频点组成的正余弦分量向量;εk为kT时刻的输入量yk与拟合WTXk之间的误差;调节增益因数μ可以在保证迭代稳定的前提下加快收敛速度。
3 基于BMFLC算法的幅值和相位补偿
针对IIR数字高通滤波器输出信号相对于实际信号存在相位超前、幅值衰减等问题,本文分别对数字高通滤波后的垂向速度和升沉位移使用BMFLC算法进行幅值和相位的补偿。修正量的大小根据IIR数字高通滤波器在每个频点处的幅频特性和相频特性求出[9]。
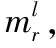
(7)
(8)
(9)
式中Hl(z)为第l个IIR数字高通滤波器的传递函数;T为信号采样周期。
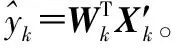
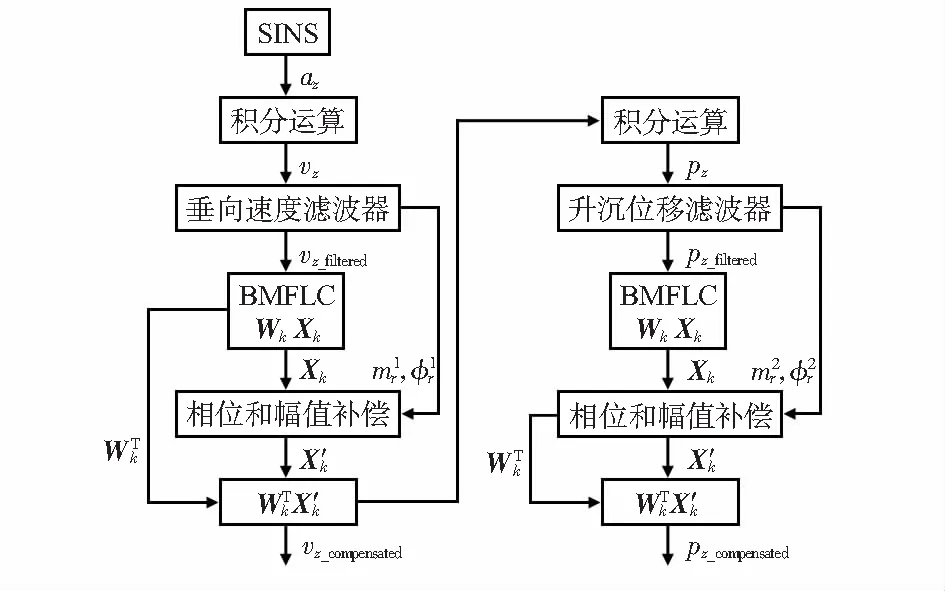
图2 改进后的升沉测量方法流程
改进后的升沉测量方法的重点在于:为了最大程度地滤除低频信号的扰动,先后进行了2次高通滤波,并分别对数字高通滤波后的垂向速度和升沉位移使用BMFLC算法进行幅值和相位补偿,从而获得较高精度的垂向速度和升沉位移。
4 仿真与转台试验
4.1 仿真试验
为了使仿真环境尽可能模拟舰船在海上的实际升沉运动,建立长峰波随机海浪模型[10],设置升沉频段为f1=0.05 Hz,fN=0.2 Hz,数据采样频率为100 Hz。设计仿真实验方案如下:第一组实验仅对垂向加速度进行两次积分与两次数字高通滤波;第二组实验在第一组实验的基础上分别对滤波后的垂向速度和升沉位移使用BMFLC算法进行幅值和相位补偿。仿真中的具体参数设置如下:BMFLC算法中设置步长Δf=0.002 Hz,增益因数μ取0.01,向量Xk,Wk的初始值为零。仿真时间为2 000 s,仿真结果如图3~图4所示。
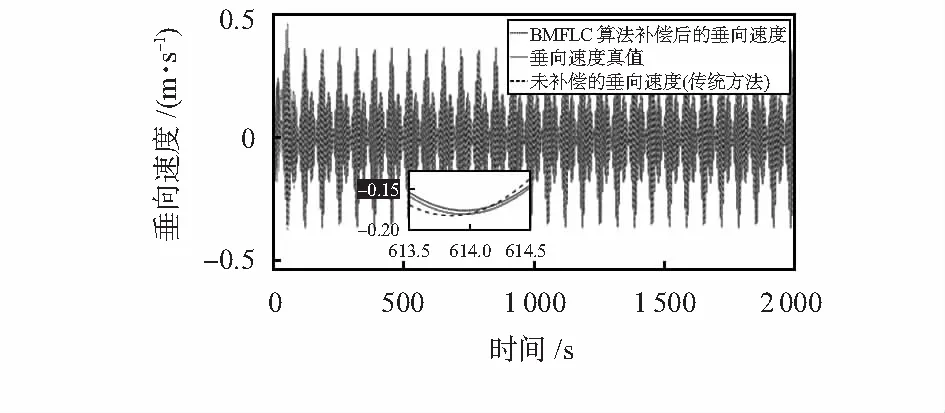
图3 基于BMFLC算法的垂向速度仿真曲线
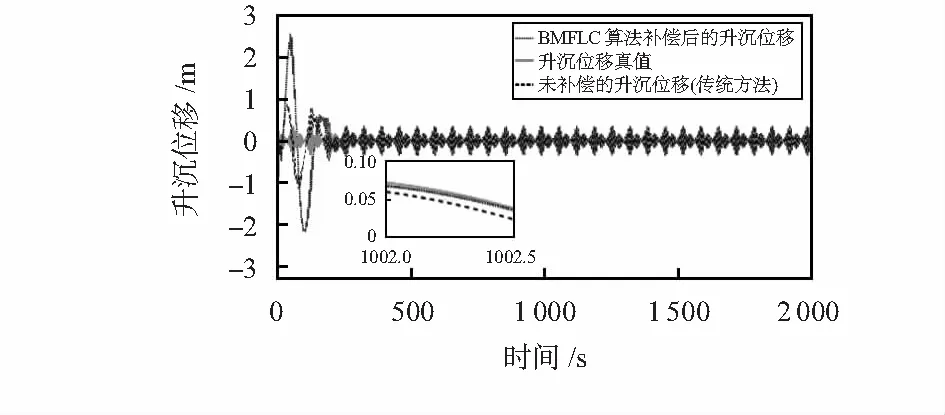
图4 基于BMFLC算法的升沉位移仿真曲线
分别对传统方法、基于BMFLC算法的升沉测量方法得到的垂向速度与升沉位移的绝对误差均值(absolute mean error,AME)与均方根误差(root mean square error,RMSE)值进行统计(统计范围为1 000~2000 s数据),统计结果分别如表1,表2所示。
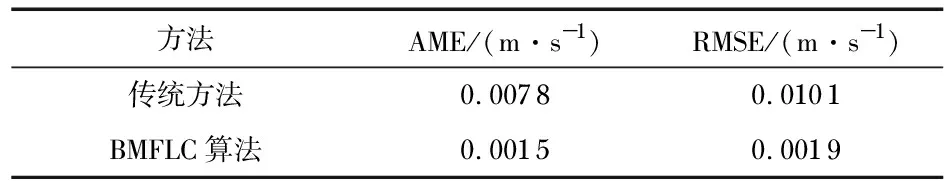
表1 仿真垂向速度测量精度统计

表2 仿真升沉位移测量精度统计
仿真实验结果表明,相对于传统方法,基于BMFLC算法的升沉测量方法得到的垂向速度的绝对误差均值缩减约80 %,均方根误差缩减约80 %;升沉位移的绝对误差均值缩减约70 %,均方根误差缩减约70 %。
4.2 转台试验
为了验证本文提出的升沉测量方法的有效性,进行转台实验。利用四自由度转台搭载捷联惯导系统做周期性垂向位移运动,试验设备如图5所示,惯性测量系统放置在物理平台上,在机电动力装置的牵引下模拟舰船的升沉运动。

图5 试验设备
具体试验如下:运行1 600 s,升沉幅值最大约0.2 m,运动周期为15 s,采样频率为500 Hz。由于该装置无法给出位移真值,故分别对滤波后的速度和位移使用MATLAB软件的无时延滤波函数filtfilt,得到的结果作为参考基准。试验结果如图6所示,传统方法、基于BMFLC算法的升沉测量方法的垂向速度误差与升沉位移误差(统计范围为1 000~1 100 s数据)分别如表3,表4所示。
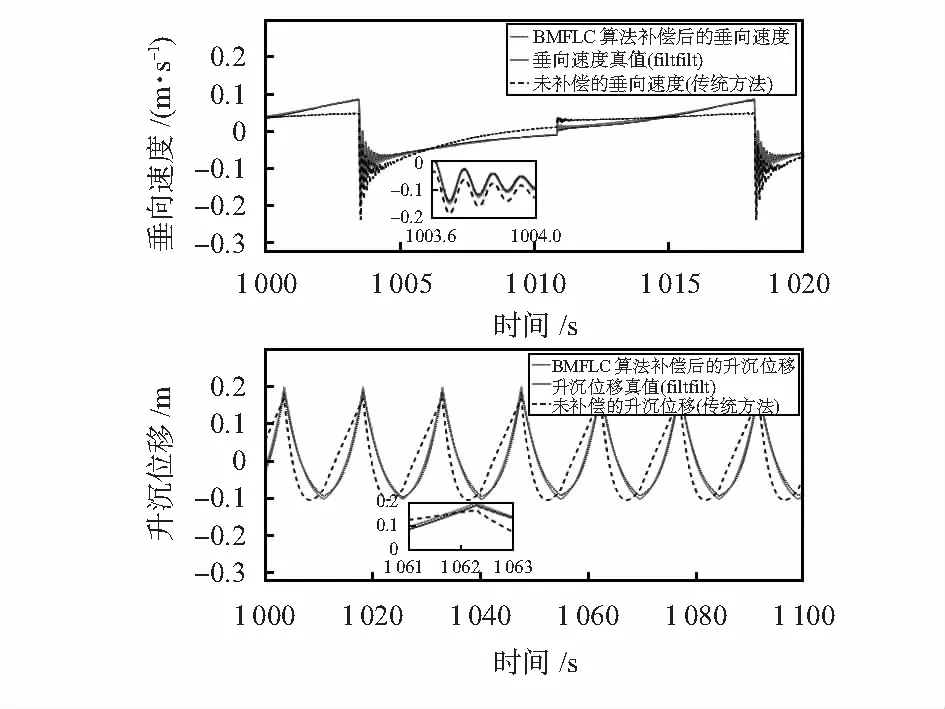
图6 转台试验结果

表3 转台试验垂向速度测量精度统计
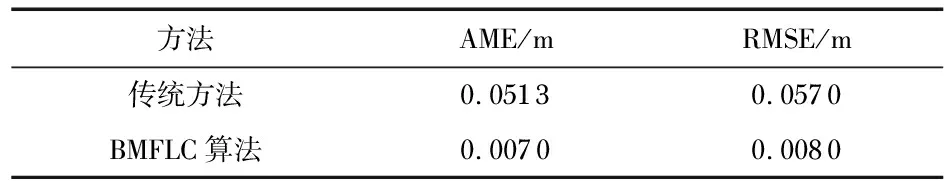
表4 转台试验升沉位移测量精度统计
转台试验结果表明,相对于传统方法,基于BMFLC算法的升沉测量方法得到的垂向速度的绝对误差均值与均方根误差均降低了一个数量级;升沉位移的误差绝对平均值与均方根误差也均降低了一个数量级。
5 结 论
本文针对IIR数字高通滤波器输出信号相位超前、幅值衰减等问题,提出了基于BMFLC算法的新的升沉测量方法。仿真与转台试验结果均表明:新的升沉测量方法能够很好地对IIR数字高通滤波器的输出信号进行幅值和相位的补偿,获得较高精度的垂向速度和升沉位移,验证了新方法的可行性。
