基于ABAQUS基础面外附加压应力数值模拟及简化方法研究

2022-10-11汪学智王超群田佳甲

山西建筑 2022年20期

汪学智，王超群，吴桐，田佳甲

(陕西中海建工程设计院有限公司，陕西西安 710075)

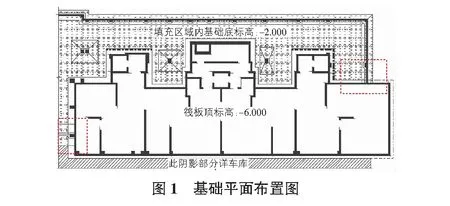
随着经济及科技的日益发展，人们对环境及建筑功能要求日益提高，越来越多的复杂建筑应运而生，复杂不仅仅体现在外立面及使用功能上，建筑地下基础的布置方案及受力形式也越来越复杂，由此带来的困扰也越来越多。例如现行规范《建筑边坡工程技术规范》对于挡土墙附加侧向土压力的计算方法虽有明确规定，但从中所列种类可看出，其荷载布置方向均不包括垂直挡土墙方向，而在实际工程中该类情况也较为常见，尤其当主楼连带商业、商业无地下室且商业条形基础与主楼基础存在高差时更为常见，如图1所示。

与挡土墙垂直的条形基础的分布荷载，对挡土墙的作用力相较之于平行方向时较小，但仍不可忽略[1-2]，工程中普遍的做法就是对该挡土墙进行适当加强，但如何加强，加强多少却比较模糊。鉴于此，本文结合实际工程，采用有限元分析软件ABAQUS对其进行数值模拟，以期得出较为贴合实际的结果，并以此为相关工程提供参考。

1 工程概况

某工程位于陕西省西安市，建筑使用年限50 a，抗震设防烈度8度，地基基础设计等级乙级。主楼为26层剪力墙结构，附带3层商业，主楼含1层地下室，商业不含地下室，根据结构布置及基础形式，主楼为筏板基础，商业基础为墙下条形基础，如图1所示。图1中虚线框中部位基础存在较大高差，使主楼挡墙平面外相接条形基础。本文则着重研究该条形基础对主楼挡土墙的平面外影响。

2 基于ABAQUS有限元数值模拟

2.1 模型参数选取

土体应力应变关系是十分复杂的，通常具有非线性、弹塑性、剪胀性和各向异性等特点，迄今为止，学者们所提出的土体模型都只能模拟某种加载条件下某类土体的主要特征[3-4]。实践证明，Mohr-Coulomb模型的参数不仅容易确定，而且其在以极限承载力为分析重点的问题中非常合适[5-7]。其塑性模型主要适用于单调载荷下颗粒状材料，适用于岩土工程中。因此，本文土体数值模拟采用该模型。

Mohr-Coulomb模型屈服面函数为：

F=Rmcq-ptanφ-c=0。

其中，φ为q-p应力面上Mohr-Coulomb屈服面的倾斜角，即摩擦角；c为材料黏聚力；Rmc(Θ，φ)按下式计算，其控制屈服面在π平面的形状。

Mohr-Coulomb模型势面函数为：

其中，ψ为剪胀角；cl0为初始黏聚力；ε为子午面上的偏心率。

土体材料本构参数采用地勘资料提供数据，本文为了研究目的的明确性，对挡土墙高范围土质材料采用均质理想弹塑性材料，以减少多余变量的干扰，土体弹性模量取值207 MPa，泊松比取值0.3，土体扩散角取值20°，材料塑性参数列于表1。

表1 Mohr-Coulomb塑性本构参数

基础及挡墙混凝土采用C30，屈服抗压强度取值14.3 N/mm2，弹性模量30 000 N/mm2。

本文采用3D可变形实体拉伸单元模拟挡土墙、条形基础及土体，并定义挡墙与土体间摩擦系数0.2，以模拟二者间的有限滑动，基础底面与土体间完全绑定，挡墙顶部限制X向与Z向位移，以模拟顶部结构板对挡墙侧移的约束，并在Load中不加载重力，由此得出的侧向压应力即为基础产生的附加侧向压应力[8]。建立ABAQUS有限元分析模型，如图2所示。为了分析研究其在特殊工况下附加侧向土压力的大小及分布规律，本文兼顾实际工程常见的基础宽度及基底压应力的范围取值，以基础基底压应力大小和基础宽度为变量，工况变量列于表2。

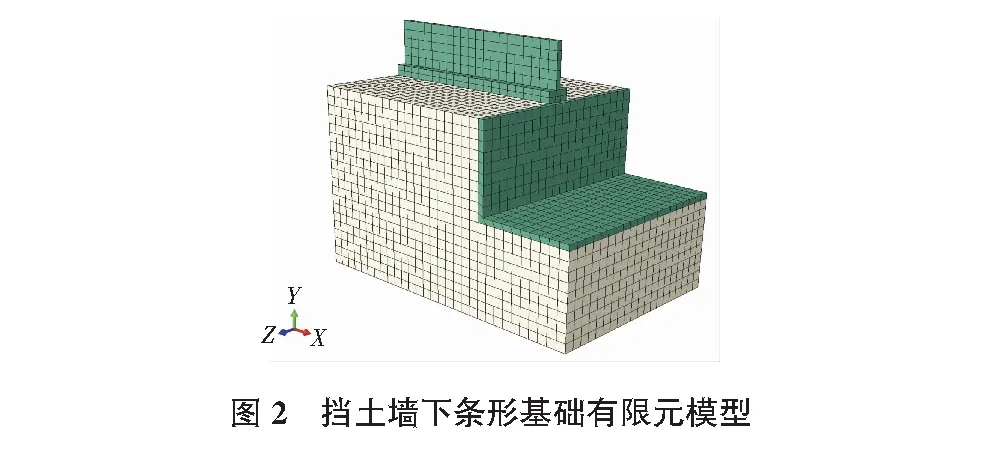
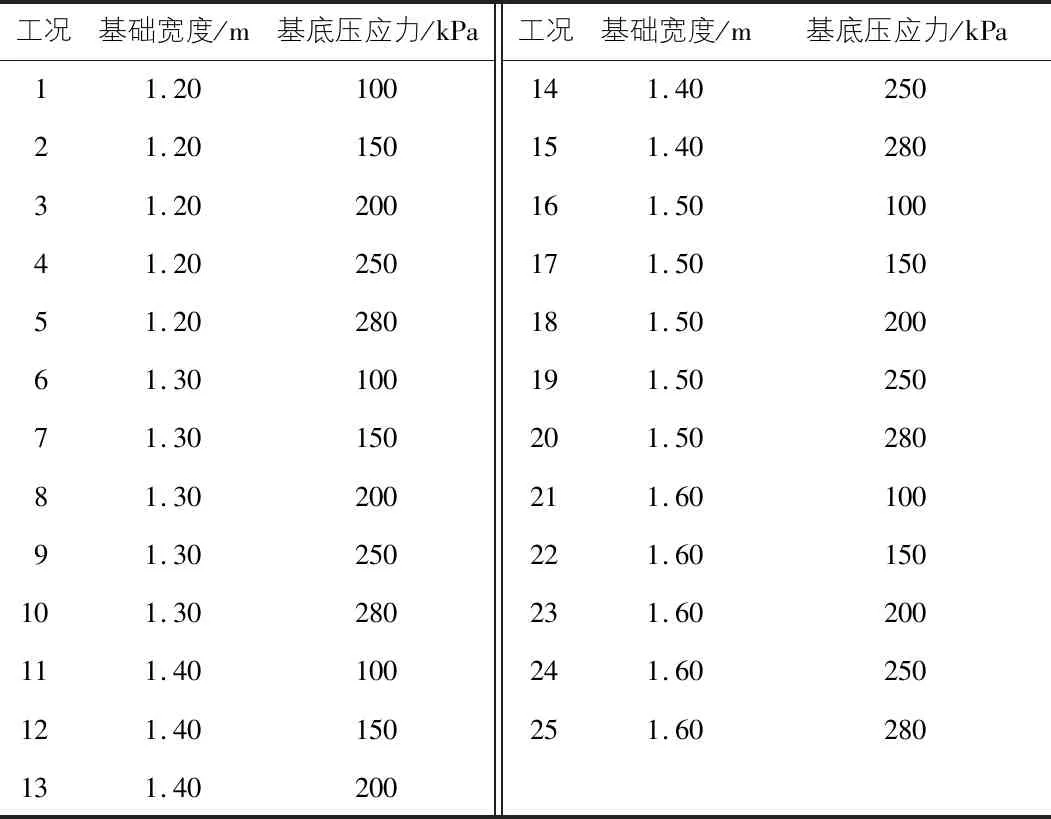
表2 挡土墙工况表

2.2 数值模拟分析

以1.20 m宽挡土墙基础在100 kPa～280 kPa工况为例，经有限元分析，得出不同工况参数下挡土墙的侧向位移，如图3所示。由图3可知，侧向位移分布呈如下规律：由于挡墙顶部结构板的侧移限值，位移随土层深度的增加先增大后减小，随距挡土墙基础水平距离的增加而减小，并且在整体受力范围内，位移均非常小，在最大基底压应力280 kPa的工况下，挡土墙最大侧向位移仅为0.54 mm，即工程中当条形基础基底压应力不超过280 kPa时，可以忽略由此产生的侧向位移。

挡土墙侧向压应力分布如图4所示。由图4可知，附加侧向压应力的大小随着深度的增加而减小，随着距挡土墙基础水平距离的增加而急剧减小，水平分布范围基本均在基础宽度范围内。不同工况下挡土墙附加侧向压应力汇总于表3。

表3中占比指挡土墙最大附加压应力与基底压应力的比值百分数。由表3可知：当基础宽度不变时，基底压应力越大，挡墙受到基础传来的附加侧向压应力也越大；当基底压应力不变时，基础宽度越大，挡墙受到基础传来的附加侧向压应力越小，最大附加侧向压应力占比也越小。

表3 挡土墙附加侧向压应力

3 工程简化方法应用研究

为了使实际工程应用较为简便实用，根据有限元模拟数据结果，曲线以一次线性曲线拟合，拟合如图5所示。由图5可知，基础宽度在1.20 m～1.40 m之间时，曲线斜率最大为0.244 3，基础宽度大于1.50 m时，曲线斜率最大为0.085 2。即当基础宽度不大于1.40 m时，挡土墙附加侧向压应力随基底压应力的增加有较为显著的增大，而当基础宽度不小于1.50 m时，挡土墙附加侧向压应力随基底压应力的增加仅有缓慢的增幅，增幅不显著。

结合文献[9-10]的研究成果，兼顾土体摩擦角、扩散角及基础宽度的变量，保证结构安全性及经济性的前提下，现对拟合方程进行简化，则有：

(基础宽度B≤1.4 m)。

(基础宽度B≥1.5 m)。

其中，x为基础基底压应力，kPa；y为挡土墙附加侧向压应力，kPa；B为基础宽度，m；c为摩擦角；φ为扩散角；K为系数，静止土压力时为0.5，主动土压力时为0.4，被动土压力时为0.6。

4 简化方法的验证

为了验证本文拟合简化公式的实用性，现对该公式进行数值模拟验证，验证项次如表4所示，其中土质参数及结构布置均按前述。

表4 公式验证

由表4可知，简化公式计算结果与有限元数值模拟结果较为接近。由于基础宽度1.4 m以内有限元数值模拟曲线较为分散，为了保证工程安全，简化公式取为曲线包络值，导致误差较大；基础宽度1.5 m以上时，曲线较为聚拢，简化公式能够较好的反映数值分析结构，并且随着基础宽度的增大，二者误差越来越小。因此，该简化公式可较好的反映有限元数值模拟的结果，能够较为安全、经济的适用于实际工程中。