基于BP神经网络的疏浚淤泥沉降预测研究★

彭 婷，谢可心，张越翔，白 洋，薛新凯，吴建奇

(江西理工大学土木与测绘工程学院，江西 赣州 341000)

1 概述

随着我国经济的快速发展，我国沿海地区部分城市土地资源日趋紧缺，为缓解土地资源紧缺，海涂围垦已广泛应用于我国沿海城市。而为保证港口、航道的畅通，我国每年将会清理出数亿立方米疏浚淤泥，为保护环境，将疏浚淤泥作为海涂围垦的填料是最有效的方法之一[1-2]。疏浚淤泥地基的加固处理方法较多，目前使用较为广泛的为真空预压法，即向疏浚淤泥地基中插入竖向排水板，通过向排水板内抽真空，在真空负压的作用下，将地基中的水和气通过竖向排水板向外排出，以加固地基。由于疏浚淤泥中含有较多黏粒和有机质，且具有沉降量大、含水率高以及固结变形持续时间长等工程特性，进行长期沉降观测投入资源较多，因此，有必要选择合适的沉降预测模型以代替长期沉降观测。此外，疏浚淤泥地基真空预压法处理的目的不仅要求处理后满足强度要求，还应满足施工期间地基沉降的工程设计要求[3]。因此，如何对真空预压法处理疏浚淤泥进行沉降预测显得尤为重要[4-6]。

虽然目前对疏浚淤泥地基的固结沉降特性的研究成果较为系统，但由于疏浚淤泥具有较为复杂的工程特性，故沉降预测分析中存在一些不确定性因素，因此，沉降计算预测结果与实测结果具有较大差异[7]，曲线拟合方法预测疏浚淤泥地基沉降与实际观测沉降之间会存在较大差距，使最终预测结果较难达到工程设计要求。本文针对温州海涂围垦的疏浚淤泥进行了真空预压法的室内模型试验，并记录了疏浚淤泥固结过程中的沉降数据，利用BP人工神经网络以及大量实测样本数据，找出适应于真空预压法处理疏浚淤泥沉降数据的BP神经网络模型，研究了疏浚淤泥的沉降量随时间的变化规律。并与曲线拟合方法推算出的沉降量进行比较，以研究该法的优越性。

2 BP神经网络

神经网络是现代信息处理的一种新兴实用的方法，它模拟人脑神经系统的计算机处理模式，由一系列简单的高度互联的处理单元组成，将传统函数的自变量和因变量作为输入和输出[8]。人工神经网络处理各类复杂非线性问题的研究中，目前应用最为广泛的是基于误差反向传播算法的BP神经网络模型[9-11]。

3 BP神经网络预测疏浚淤泥沉降

BP网络因其简单性和从模式(即样本)中提取有用信息的能力而广泛应用于反分析。它允许指定多个输入标准和生成多个输出建议，而无需预先假设与输入变量和输出变量之间存在的相关函数形式[12-13]。

3.1 数据的采集及归一化处理

以真空预压法加固疏浚淤泥室内模型试验为例，经过长期沉降预测，获得大量数据，见表1。将0～780 h时间内沉降观测数据导入到MATLAB中，共66组数据。其中，取53组数据作为训练样本，13组数据作为验证样本，据此进行训练学习。由于BP神经网络模型输入节点的各样本数据物理量不相同，且各样本数据之间的数值相差甚远，因此，可能会出现大、小数值之间的淹没情况。为防止以上情况的出现，可通过S型正切函数“tansig”将网络输入和输出目标取值在[-1，1]范围内，经神经网络训练结束后，再将训练后的输出数据反映射回原数据范围，使网络输入更为规范，并大大提高网络收敛速率[14-16]。

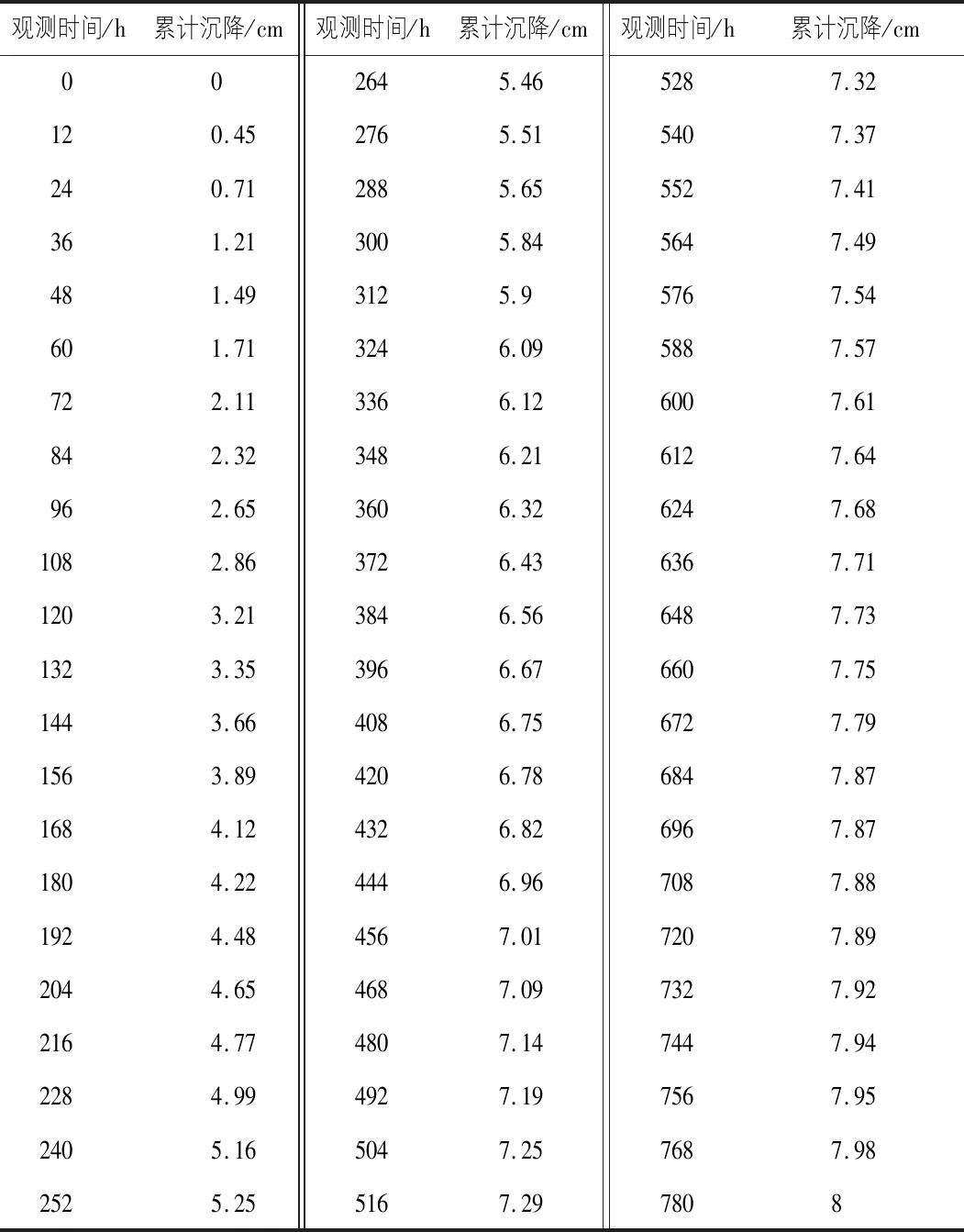
表1 沉降观测数据表

3.2 确定网络结构

如图1所示，本文所建立神经网络模型输入层神经元个数为3；隐含层神经元个数为7，输入层与隐含层之间的激活函数类型选择双曲正切S型激活函数；输出层神经元个数为1，且输出层神经元采用的线性激活函数。输出层传递函数为线性函数“purelin”，采用“traingdm”训练函数进行样本的训练。

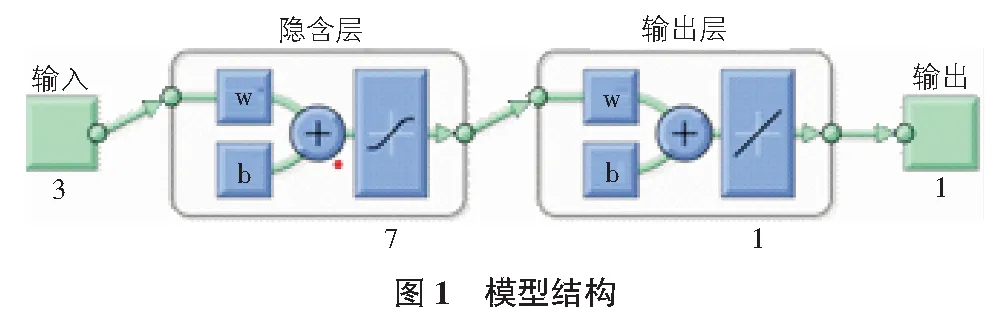
3.3 网络训练结果

为验证神经网络模型预测结果的可靠性，可将经过神经网络训练后的输出值与训练样本值进行对比，以检验网络经过训练后的效果。如图2所示，经过对样本值与输出值的对比，可以看出，经过神经网络训练后的输出值与实测值较为接近，且由图3可以看出，误差值最大为0.15 cm，最小为0.000 4 cm，由此可见，训练的网络对于后期沉降的测试结果的误差可以满足要求，本网络对实测数据的拟合效果较好。

3.4 BP神经网络沉降量预测

由之前的分析可以看出，该预测模型预测数据与实测值之间较为吻合，表明该算法较为合理，因此，可利用上述神经网络模型进行沉降量预测。由图4可知，本文以疏浚淤泥前期固结沉降观测数据作为样本数据来训练网络，另对疏浚淤泥固结后期(792 h～900 h)沉降量进行预测，其预测得到的沉降数据与实际观测沉降数据十分接近，最大误差值为0.01 cm。由此可见，当训练的样本数据足够充分可靠时，神经网络模型的预测结果是十分精确的。通过疏浚淤泥后期固结沉降实际观测数据与神经网络模型的沉降预测数据进行对比，预测得到的数据与实际沉降观测数据基本一致，表明该预测模型的可信度较高。

3.5 曲线拟合法

3.5.1 双曲线法

双曲线法是假设平均沉降速度是以双曲线形式减少的经验推导法，双曲线法认为沉降曲线在点(t0，S0)后，监测时间t时刻对应的沉降量St为：

(1)

由式(1)推导得出：

Nav_to_goal初步实现将机器人导航到目标点。算法假设当前位置与目标点之间没有障碍物。将机器人的速度和转向控制分为3个步骤：首先调整机器人位姿使之面向目标点；然后驱动机器人接近目标点，用插值法平滑运动过程的速度；到达目标之后旋转机器人朝向以满足下一步骤的准备。在这个过程，节点使用tf库的TransformStamped函数，将Rovio当前的位置转化为其在target_frame的坐标。

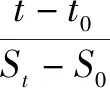
(2)

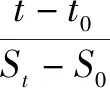
由试验实测数据发现，在抽真空24 h后，土体内的真空度已经达到稳定状态，由此，取t0=24，S0=0.71 cm，由沉降实测值与式(2)得式(3)：

(3)

本试验在第900 h时停止试验，故取时间t=900，由式(3)可得，St=8.29 cm。沉降拟合曲线如图5所示，由于试验前期，土体排水固结较快，沉降较不稳定，在拟合时，数据较为离散，因此会产生一定的误差，从而影响最终沉降量的预测。

3.5.2 三点法

三点法[17]认为当实测沉降值基本趋于稳定时，可利用三点法求得最终沉降值，在沉降-时间曲线上以t3-t2=t2-t1的要求选取(S1,t1),(S2,t2),(S3,t3)，并按式(4)进行最终沉降值的计算：

(4)

其中，S1,S2,S3分别为t1,t2,t3时刻的沉降值；S∞为最终沉降值。取时间t1=540 h，S1=7.37 cm；t2=660 h，S2=7.75 cm；t3=660 h，S3=8 cm，通过计算，最终沉降值为8.48 cm。由于三点法的计算与选定的数据样本及时间间隔有关，根据不同的数据样本及时间间隔，会得到不同的最终沉降量，因此，由于人为因素的影响，会存在较大误差。

Asaoka提出了一种图解法[18]，将恒定时间间隔所对应的一系列沉降数据，在以Sj-1为x轴、Sj为y轴的坐标系中以坐标点(Sj-1,Sj)画出，并给出了以下表达式：

Sj=β1Sj-1+β0

(5)

其中，β0和β1的值可作为Sj～Sj-1拟合直线的截距与斜率，当时间无穷大时，则：

(6)

对直线进行拟合，拟合直线如图6所示，并利用上式求得最终沉降值为9.02 cm。与三点法相似，当选定的数据样本与时间间隔不同时，亦会存在不同的最终沉降计算值，此外，由于Asaoka法在求解最终沉降量时，对时间取极限，将会导致最终沉降量的计算值偏大，从而影响最终沉降量的预测。

3.6 预测结果比较

由图4可以看出，经BP神经网络预测后，利用真空预压法加固疏浚淤泥后的最终沉降量为8.15 cm。通过表2可以看出，采用相同的数据进行预测，经BP神经网络预测后的最终沉降值与实际观测值之间产生的误差值相对较小，对工程的预测更为合理。

表2 最终沉降量预测结果汇总表

4 结论

对于温州地区疏浚淤泥地基真空预压法的处理，沉降量较大，研究其固结沉降的过程是有必要的。BP神经网络法与曲线拟合法有着根本的不同，它的训练样本可以从第一次观测时提取，可以忽略曲线拟合法沉降预测过程中人为因素的影响，更能表现出疏浚淤泥地基沉降的发展趋势和规律。从表2的预测结果来看，与曲线拟合法预测沉降相比，利用BP神经网络法预测的沉降结果与实际观测的沉降结果之间误差较小，可信度较高。虽然神经网络方法并不是从固结沉降机理上分析和计算疏浚淤泥地基固结沉降，但是它为沉降预测提供了一种与传统曲线拟合法完全不同的新思路，具有广阔的工程应用前景。