基于孔隙纵横比谱反演的饱和岩石宽频段岩石物理模型

韩旭，王尚旭，刘浩杰，刘韬，唐跟阳*

1 中国石油大学(北京) 地球物理学院，北京 102249

2 中国石化胜利油田物探研究院，山东 257000

3 中国石化石油勘探开发研究院，北京 100728

0 引言

岩石的速度主要受孔隙度、矿物成分、流体类型和饱和度控制[1]。大量实验室研究表明，干岩石的弹性速度或弹性模量随着有效压力的增加而显着增加[2-4]。这种压力依赖性通常可以通过裂缝根据其纵横比逐渐闭合来解释[4-5]。虽然这些裂缝只占孔隙空间的一小部分，但相比于球形孔，它们对多孔岩石的有效速度有更加显著的影响。通常来说，Gassmann理论模型由于忽略岩石孔隙结构影响，往往不能解释岩石弹性性质的压力依赖性。在实验室条件下使用超声波测量的实验数据证实了孔隙结构对声速的重要性[6-8]。已经建立了许多理论公式来将有效弹性特性与孔隙结构相关联。由于岩石中孔隙空间的复杂性，通常假设它们可以由以其纵横比为特征的椭球体表示，这些椭球状孔隙可以表征各种各样的孔隙形状，并且可以通过Eshelby(1957)的单一椭球体等效夹杂理论进行分析处理[9]。典型的此类理论包括 K-T 模型和 DEM 理论[4,10-12]，它们将椭圆形孔隙视为岩石固相中的包含物。Shapiro(2003)利用双重孔隙结构模型解释岩石速度随压力的这种非线性/线性变化现象，利用孔隙纵横比α表征孔隙形状[13]。孔隙可以视为具有不同形状的硬孔隙(α＞ 0.01)和软孔隙(α＜0.01)的组合[14]。这种双重孔隙度模型很好地解释了有效压力下速度的非线性到线性变化的特征。Cheng and Toksöz (1979)提出了一种与压力相关联的孔隙纵横比和孔隙闭合的关系式，通过超声测量的干燥和饱和速度反演孔隙和孔隙纵横比的离散型分布[15]。该模型适用于超声频段，并且不考虑流体效应。

另一方面，对于流体饱和岩石，压力和频率的影响是耦合的，因为它们通过孔隙的微观结构相互连接[16]。不同形状和方向的孔隙之间的局部流体流动是流体饱和岩石中弹性波的频散和衰减的主要原因之一[17]。孔隙结构对岩石弹性参数的影响会因流体与裂孔微观结构的相互作用而进一步复杂化。在喷射流模型中，软孔孔隙度是造成弹性速度频散的主要因素之一，喷射流特征频率与软孔隙的纵横比有关[18]。Gurevich et al(2010)提出了一种简单喷射流模型[19]，其中孔隙的纵横比以及微裂缝的含量是造成饱和流体岩石频散与衰减的主要因素。但是，该理论模型只是给出了单一孔隙纵横比以及微裂隙含量对弹性模量频散与衰减的影响，该假设不符合真实岩石的孔隙结构。并且，这些理论都有许多表征孔隙形状的“自由”参数(例如孔隙纵横比、软孔孔隙度等)。这些参数是未知的，通常需要拟合实验数据获得的。这会降低这些模型的拟合能力和实用性，因为良好的拟合不足以证明模型的适用性。

本文的目标是克服这种不确定性，并从速度或弹性模量的压力依赖性获得此类参数。通常，孔隙形状和孔隙度可以表征岩石弹性参数的压力依赖性，可以使用对这种依赖性的分析来估计这些参数。Shapiro (2003)提出的干速度压力依赖性理论模型[13]。然而，模型中的软孔隙假设具有相同的纵横比。这种将岩石的孔隙纵横比简化为单一纵横比的方法无法完全表征岩石微裂隙的分布，通常岩石的孔隙纵横比具有较宽的范围。利用实验测量获得的岩石速度与压力的相关性，并计算岩石软孔隙纵横比的分布，可以更为有效的获取岩石孔隙纵横比的分布。Cheng and Toksöz(1979)将实验室测量的各种岩石的地震速度作为压力和饱和度相关的函数进行反演，得到它们的孔隙形状谱[15]。这种反演是基于孔隙闭合作为压力和速度变化的函数的理论。通过超声测量的干燥和饱和速度反演孔隙度和孔隙纵横比的离散型分布，但是该方法忽略了流体流动效应。

本文扩展了原有的岩石物理模型。首先，利用超声测量的速度-压力变化曲线来反演孔隙纵横比分布及其孔隙度。其次，基于K-T等效介质模型将干燥硬孔隙加入岩石基质中，并再次加入饱和软孔隙(软孔隙中添加流体频变体积模量)获得岩石“干骨架”的弹性模量；最后利用Gassmann流体替换理论描述硬孔隙中饱和流体对弹性模量的影响。

1 岩石物理实验

为了研究复杂孔隙结构岩石速度的压力和频率依赖性，本文选取了中国东部油田沙河街组的致密砂岩样品进行超声速度测量。致密砂岩样品的孔隙度为4%，密度为2644 kg/m3。样品的矿物含量通过XRD衍射仪获得，并利用VRH等效介质理论模型计算样品的基质体积模量(Ks=55 GPa)和剪切模量(μs=29.6 GPa)。样品所饱和的液体为68#白油(体积模量2 GPa，密度890 kg/m3，黏度0.068 Pa·s)。采用超声透射法测量不同压力下不同流体饱和样品的弹性参数。

超声波透射法是利用一对超声波换能器激发和接收在岩石样品中传播的超声波P波或S波，记录接收到的波形并用于速度计算。 换能器的直径为17 mm，激励频率约为1 MHz。在测量过程中，温度保持在20 ℃，压力从0 MPa增加到50 MPa。首先，对致密砂岩样品进行润湿以软化“过干燥”样品。将其放入充满水蒸气的密封容器中48小时，以软化岩石骨架。在下一步中，使用“伪自吸”方法将样品浸入油中，该方法首先将样品浸入油中，抽真空，然后在50 MPa下加压长达7天。然后，测量了油饱和致密砂岩的超声波速度。

图1显示了不同压力下致密砂岩样品的纵波和横波速度。比较了这些测量结果，发现在干燥条件下，超声速度的变化随压力从非线性增加变为几乎线性增加，转变压力约为30 MPa。当样品充满液体时，速度随着压力的增加而变化更加平滑，不会表现出非线性/线性转变。随着压力的增加，干燥和油饱和条件下的纵波速度之间的差异减小，在干燥和油饱和条件下横波速度差小于纵波速度差。速度曲线表明压力对超声速度的影响很大，随着压力的增加，岩石样品中的软孔隙逐渐闭合[14]。在低压范围(0～30 MPa)的非线性趋势下，纵横比小的软孔隙逐渐闭合，表明软孔隙度是速度变化的主要控制因素。在高压范围(30～50 MPa)的线性趋势下，软孔隙几乎闭合，表明硬孔隙是速度变化的主要控制因素[14,16]。

2 岩石物理建模

2.1 孔隙纵横比谱反演

上述致密砂岩实验结果表明，速度随压力的非线性到线性变化趋势与双重孔隙结构(球型硬孔隙与裂缝型软孔隙)模型一致。为此，遵循 Cheng and Toksöz (1979) 提出的反演方法[15]，从超声波速度-压力曲线关系中反演孔隙纵横比谱。对于具有岩石基质(岩石矿物颗粒)模量Ks，μs和孔隙填充物模量Ki，μi的两相材料，Kuster and Toksöz (1974)给出了等效模量K*和μ*的表达式：

其中，αm是第m个纵横比，c(αm)是它在相关的孔隙度。T1和T2是由背景材料的体积模量Ks和剪切模量μs以及孔隙填充物的体积模量Ki和剪切模量μi组成的表达式，该参数反映孔隙形状影响的耦合因子。在 Cheng and Toksöz (1979)中给出了它们的明确表达[15]。

根据Eshelby (1957)对椭圆形包含物的定义[9]，Toksöz 等(1976)给出了孔隙体积分数dc/c随压力P变化的表达式[20]。

其中，Ei是纵横比和有效模量的表达式，KA是静态干体积模量，通常用超声波速度计算的干体积模量近似。在Cheng and Toksöz (1979)中给出了它们的明确表达[15]。通常认为d/ 1c c＜－，假设裂缝是闭合的。微裂隙在压力Pn下的大小与其在零压力下的大小的关系为：

对于纵横比为α和半长轴为a的扁球状孔隙，c(α) =4παa3/3。孔隙纵横比随压力的变化由下式给出：

因此，可以将孔隙纵横比的变化与其在零压力下的状态联系起来：

将方程(4)代入方程(1)和(2)并得到：

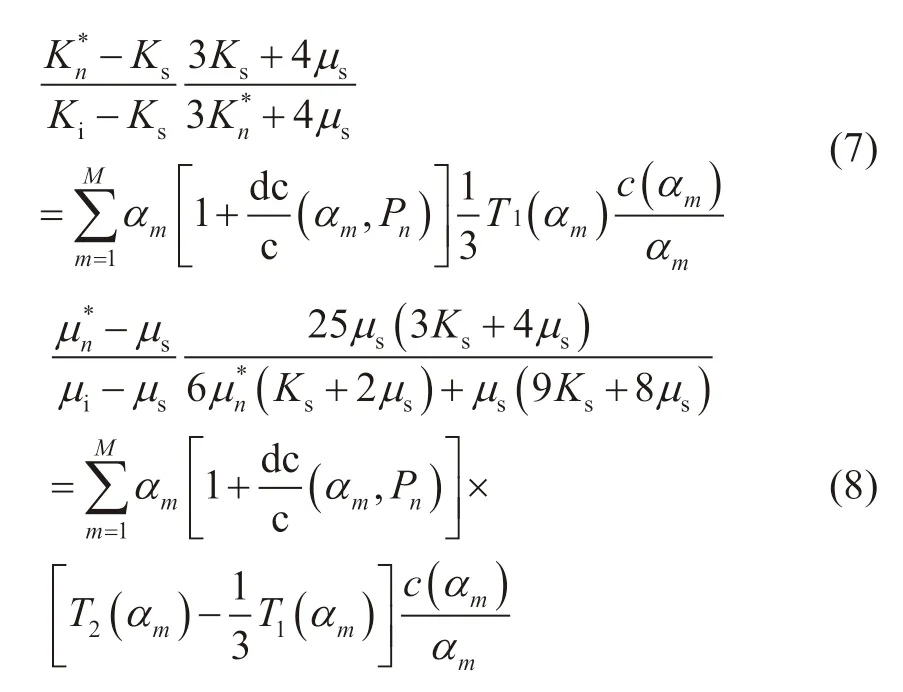
等式(7)和(8)具有y=Ax的形式，其中，Kn*和μn*是超声条件在不同压力下测量的弹性参数。为了使矩阵A更加稳定，选择参数向量x为c(αm)/αm而不是c(αm)。这样，模型向量x的元素大约在0.1和1之间。方程总数为2LN，其中L表示饱和度数，N表示压力数。m是压力点的数量或纵横比。模型向量x的维数为m-1，因为它应满足所有纵横比的孔隙度之和等于总孔隙度ctotal。

系数矩阵A的维数为2LN×m-1，因此系统y=Ax是一个超定线性方程组。通过最小二乘法转换A[21]。

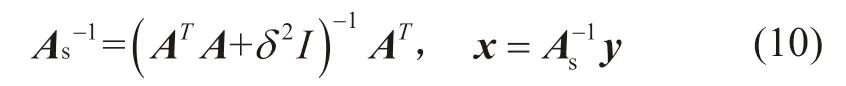
其中，δ是与ATA的最小特征值相关联的可调参数。

图2a显示了致密砂岩样品在0 MPa下的离散孔隙纵横比谱。纵横比的分布显示了典型的双孔隙模型的特征。硬孔隙在致密砂岩的总孔隙度中占主导地位。在零压力下，软孔隙度具有相当宽的纵横比范围(10-3～10-4.5)，软孔孔隙度为0.03%，而硬孔孔隙度为3.98%。图2b为不同压力下的孔隙纵横比谱。硬孔孔隙度随压力的增加几乎保持不变，而软孔孔隙度的数量随着压力的增加逐渐减少，数值逐渐减小。表明这些软孔隙随着压力的增加而逐渐闭合(孔隙度小于10-8基本闭合)。图3为不同压力条件下，软、硬孔隙度的绝对值变化曲线。如图3所示，硬孔隙基本不随压力的变化而变化，而软孔隙度随着压力的增加逐渐降低，当压力达到50 MPa，软孔隙度基本为0。

图2 致密砂岩样品反演孔隙纵横比谱结果Fig.2 Inversion pore aspect ratio spectrum results of tight sandstone samples

图3 软、硬孔孔隙度随压力的变化曲线Fig.3 Variation of compliant and stiff porosity with pressure

图4是干燥条件下超声实验测试结果以及K-T模型的模拟结果。基于离散孔隙纵横比谱的K-T模型对速度有很好的拟合结果。由于线性迭代反演方法依赖于有效介质理论，因此没有考虑流体流动效应。如果除了干数据之外还使用饱和岩石样品的速度，它会在孔隙纵横比谱的反演中引入误差。利用干燥数据反演的孔隙纵横比谱能够更加准确的计算岩石的孔隙结构。当样品只含有硬孔隙时，样品的纵横波速度不随这压力的变化而变化，在压力范围(40～50 MPa)模拟结果和实验结果有很好的拟合关系。然而，在低压力范围，模拟结果与实验结果差异较大，因此，软孔隙度是岩石速度的主要控制因素。

图4 基于干燥数据反演孔隙纵横比谱的K-T模型模拟结果，红线为只含有硬孔隙的模拟结果Fig.4 K-T model simulation results of inversion of pore aspect ratio spectrum based on drying data, the red line is the simulation result with only stiff pores

2.2 “干骨架”弹性模量计算

对于饱和流体岩石，流体流动机制是解释岩石速度频散的主要理论之一。基于K-T等效介质模型和反演的孔隙纵横比谱的结果，计算岩石样品的“干骨架”弹性模量。其中，硬孔隙中不添加流体，软孔隙中加入流体频变体积模量[22]。

对于液体饱和岩石，超声频率下的修正骨架模量与干骨架模量相关[19]，公式为：

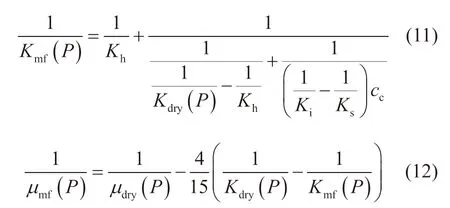
其中，Kmf和μmf是修正干骨架的体积模量和剪切模量。Kh是不含有软孔隙岩石的体积模量，cc是软孔孔隙度。

对于中间频率，Gurevich 等(2010) 表明模量遵循相同的方程(11)-(12)但流体模量Ki由与频率相关的(ω)代 替[19]。Glubokovskikh等(2016)简 化 和 概 括了Gurevich et al.(2010) 的方法[22]。对于具有动态黏度η的孔隙流体Kf*(ω)，其相应表达式由Tsai and Lee (1998) 给出[23]：

其中，Jk是k阶的第一类修正贝塞尔函数，而μf*(ω) =iωη。

首先，基于K-T模型将硬孔隙加入到岩石基质中，硬孔隙的含量可通过反演的孔隙纵横比谱获得。

其中，Kh和μh是只含有硬孔隙岩石的弹性模量，α13－是模拟出的硬孔隙纵横比，c(α13－)是硬孔孔隙度。这里我们只把纵横比大(α＞0.01)的硬孔孔隙度带入到K-T模型中，可获得不含有微裂隙岩石的干骨架模量Kh和μh。

其次，在高频极限下，修正的“干骨架”的体积和剪切模量由等式(1)-(2)定义。继续添加饱和流体频变体积模量的软孔隙，通过用Kf*(ω)和μf*(ω)替换方程(1)-(2)中的流体体积模量Ki和μi来获得较低频率的模量，其中，Kh和μh可以通过方程(15)-(16)计算得到。

2.3 全饱和岩石弹性模量计算

最后，全饱和岩石弹性模量由Gassmann流体替代方程计算[24]。

式中，Ksat和μsat是全饱和岩石体积模量和剪切模量。cs是硬孔孔隙度。

图5a是新模型和K-T模型对超声速度的拟合结果。需要说明的是，孔隙纵横比谱的反演不涉及全饱和速度数据。在超声频段，K-T模型和喷射流模型对P波和S波都具有很好的拟合结果。图5(b)是喷射流模型、K-T模型和Gassmann模型对体积模量频散的模拟结果。如图所示，在超声频率范围内，流体饱和样品的建模速度对于新模型和等效介质模型(K-T)没有太大差异。在低频范围内，流体饱和样品的Gassmann模型与改进模型的低频极限相同。因此，新模型的高频极限符合等效介质模型，而低频极限符合Gassmann理论。相比于简单喷射流模型，新模型由于考虑了孔隙纵横比谱，频散范围更宽。

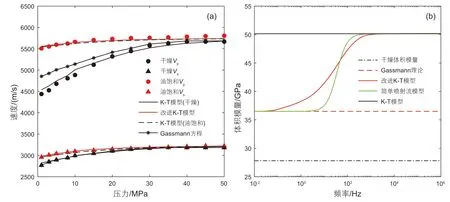
图5 (a)致密砂岩超声速度与改进K-T模型和K-T模型的拟合结果；(b) 4种模型模拟致密砂岩体积模量随频率的变化关系Fig.5 (a) The ultrasonic velocity of the tight sandstone and the fitting results of the improved K-T model and the K-T model; (b) The relationship between the bulk modulus of the tight sandstone simulated by the four models with frequency

图6显示了不同压力条件下，P波速度和S波速度频散的结果。106Hz的数据点是对于压力和油饱和条件下的超声P波和S波速度。通过孔隙纵横比分布，新模型可用于模拟弹性参数的压力和频率依赖性。从模拟结果可以看出，速度的特征频率随压力增加而减小，而速度频散量降低。随着压力的增加，样品的软孔隙的平均纵横比和孔隙度不断下降。较低的纵横比会导致特征频率降低，而软孔孔隙度的降低会导致频散幅度下降[19,25-28]。

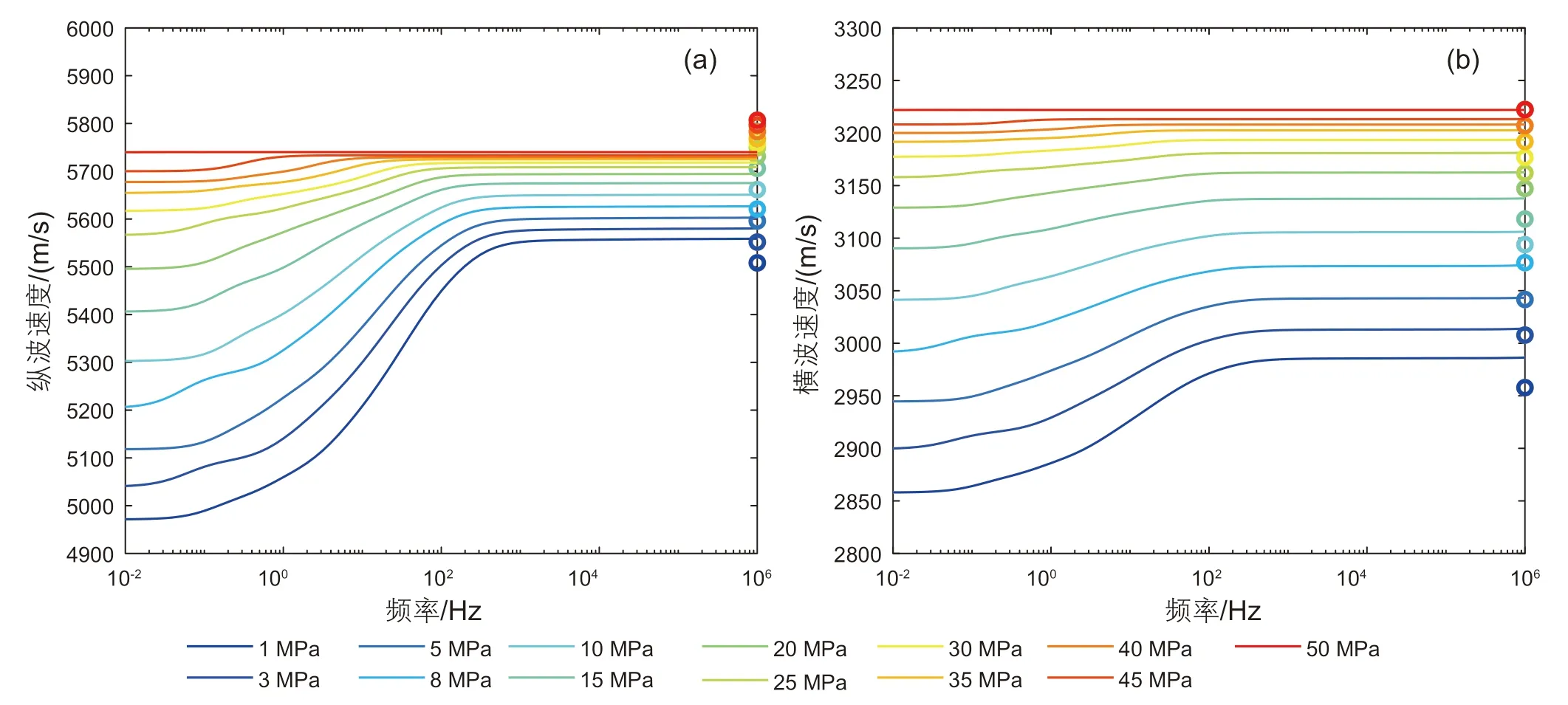
图6 不同压力条件下速度频散的模拟结果 (a)纵波速度; (b)横波速度Fig.6 Simulation results of velocity dispersion under different pressure conditions (a) P-wave velocity; (b) S-wave velocity

3 讨论

基于不同压力下的孔隙纵横比谱，在干燥和完全饱和条件下，新模型可以很好地预测致密砂岩P波和S波速度(图4a)。在超声频率范围内，对于新建立的岩石物理模型和有效介质模型，流体饱和样品的建模速度没有太大差异。这里同样采用Gassmann理论模型来解释致密砂岩饱和油的超声速度。结果表明， Gassmann理论模型忽略了孔隙结构的影响，模拟结果完全低估了实际测量结果。因此，相比于Gassmann理论模型，新建立的模型具有更高的精度。同时，该模型的一个优点是不需要可调参数。输入参数和变量来自独立的实验室测量，建模结果具有可验证性。实际测量和建模结果都表明，压力和频率对弹性模量的影响是耦合的，因为这两个因素与孔隙微观结构是紧密联系在一起的。压力的变化将引起孔隙结构的改变(孔隙纵横比和软孔孔隙度)，而孔隙结构的改变会影响岩石速度频散的大小和特征频段。另外由于缺乏低频数据，可以利用低频数据进一步验证模型的适用性。

4 结论

岩石微观孔隙结构不仅是干燥岩石速度的主要控制因素，也决定了饱和流体岩石中与流体流动相关的速度频散和衰减作用。为了研究压力和频率对流体饱和岩石弹性模量的影响，本文根据干燥条件下超声速度-压力曲线变化来反演孔隙纵横比谱。基于这种复杂的孔隙结构，本文扩展了原有的模型来解释速度的压力和频率依赖性。在所提出的模型中，孔隙空间由两部分组成：具有纵横比分布的软孔隙和纵横比大的硬孔隙。通过定量表征软孔隙闭合过程，获得了软孔隙每个压力下的纵横比分布。在软孔隙中加入了流体频变体积模量，使模型具有频散效应。相比于简单喷射流模型，新模型由于考虑了孔隙纵横比谱，频散范围更宽。模型对与压力相关的超声数据有很好的拟合结果。新建立的模型对速度频散给出合理的理论解释。因此，该研究有助于我们更好地了解流体诱发地震波衰减和频散的特征。